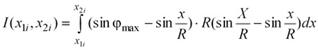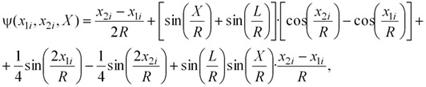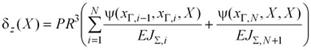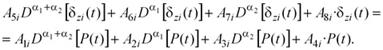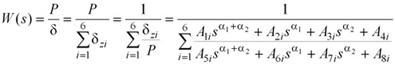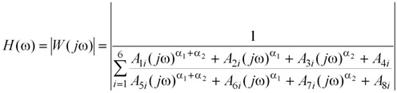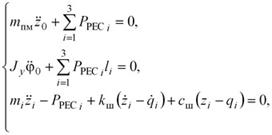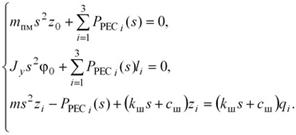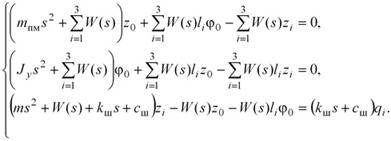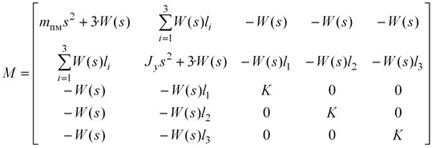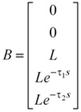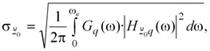научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 07, июль 2011
УДК: 629.373.3, 629.3.027.3, 539.37
МГТУ им. Н.Э. Баумана
koleso49@mail.ru
Введение
Проведенный анализ конструкций систем подрессоривания современных транспортных средств показал, что полимерные композиционные материалы (ПКМ) находят свое применение в транспортных средствах, для которых снижение снаряженной массы является критическим показателем. Применение рессоры из ПКМ позволяет снизить массу упругого элемента в 3…5 раз, увеличить долговечность в 4…5 раз, при этом улучшается плавность движения, снижается шум, повышается безопасность движения. При замене стальной многолистовой рессоры на рессору из ПКМ уменьшается масса неподрессоренных частей автомобиля, уменьшается динамическая нагруженность подвески, улучшаются экономические показатели колесных машин (КМ) [1, 2].
Известны конструкции виброизоляторов на основе ПКМ и полимерных резиноподобных материалов. Однако, единого метода создания и прогнозирования упругодемпфирующих свойств таких элементов в составе систем подрессоривания КМ нет. Кроме того, определенной мерой демпфирования (сухого и пропорционального перемещению) обладает любая рессора. В работе рассматривается возможность использования гистерезисного демпфирования ПКМ в системе подрессоривания ВТС.
Целью исследований в рамках данной статьи является разработка метода прогнозирования вязкоупругих свойств и способа моделирования механического поведения листовых рессор из ПКМ в системах подрессоривания КМ.
Часть I. Математическая модель вязкоупругого поведения рессоры под нагрузкой
Решение задач вязкоупругости опирается на принцип Вольтерра, согласно которому решение линейной задачи вязкоупругости может быть получено из решения соответствующей задачи линейной теории упругости путем замены в нем констант упругости некоторыми операторами.
В данной статье используются механико-математические модели вязкоупругой среды, сводящиеся к закону Гука с помощью операторных представлений.
| , |
где Q(s) и R(s) — некоторые операторные полиномы, соответствующие выбранной вязкоупругой модели.
Существует множество реологических моделей, описывающих нелинейные свойства материалов. В данной статье рассматриваются модели, основанные на применении математического аппарата производных дробного порядка [3, 4, 5, 6].
Дробно-дифференциальный подход, развитие которого в реологии связано с именами Скотта–Блэра, Бэгли и Торвика, Горенфло и Майнарди, Фридриха и Шисселя, Блюмена и Метнлера, Нонненмейкера и Глекля, Клафтера и Шлесингера, был успешно применен для описания реологического поведения органических стекол, эластомеров, полиуретана, полиизобутилена, монодисперсного полибутадиена, твердых аморфных полимеров в широкой области температур.
Для полимерных материалов, входящих в состав рессоры, используется уравнение состояния модели стандартного линейного тела в дробных производных:
| (1) |
впервые предложеное Капуто и Майнарди в 1971 г с использованием дробных производных Капуто [3] как эмпирическая модель, позволяющая более точно воспроизвести данные эксперимента.
Операторные полиномы для этой модели имеют вид:
| , |
| , |
где α, τ, θ — вязкоупругие константы материала.
Тогда упругий оператор, соответствующий модулю Юнга первого рода при учете вязкоупругости будет иметь вид:
| . | (2) |
Таким образом, для учета вязкоупругих свойств материалов необходимо составить уравнение их поведения под нагрузкой исходя из постановки задачи в рамках линейной теории упругости, затем произвести замену модуля Юнга на операторное соотношение и, вернувшись к оригиналам по Лапласу силовых и кинематических факторов, получить дифференциальное уравнение, описывающее вязкоупругое поведение материала.
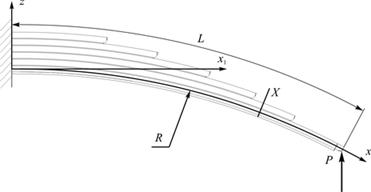
Рассмотрим расчетную схему четверть-эллиптичечкой рессоры, изображенную на рисунке 1. Задача изгиба рессоры в рамках линейной теории упругости решается с помощью интеграла Мора.
Рис. 1. Расчетная схема рессоры
Изгибающие моменты в сечении x от силы P и единичной силы, приложенной в сечении X, равны:
| , |
| , |
где φmax = L/R – максимальный угол, соответствующий углу поворота сечения в точке приложения силы P на конце рессоры.
Совместная работа нескрепленных жестко листов рессоры определяется их совместным изгибом. При этом суммарный момент инерции сечения определяется суммой моментов инерции всех листов сечения. С учетом того, что листы выполнены из различных материалов будем искать суммарную жесткость сечения по соотношению:
| , | (3) |
где EK, bKi, hKi — модуль Юнга композиционного материала, ширина и толщина листов из ПКМ,
EР, bРi, hРi — модуль Юнга листоа полимерного межлистового материала, ширина и толщина листов,
EС, bСi, hСi — модуль Юнга стальных листов, ширина и толщина стальных листов.
Рассматривая интеграл
| , |
на каждом участке с постоянной жесткостью получим:
| , |
где
| , | (4) |
x1i, x2i — начальная и конечная координаты i-го участка.
Преобразуем выражение (4):

Таким образом, приходим к выражению:
| . |
Выражения ψ(x1i, x2i, X) для всех участков, кроме последнего имеют вид:
| (5) |
а на последнем участке, в зависимости от расположения сечения X, выражение (5) приобретает вид:
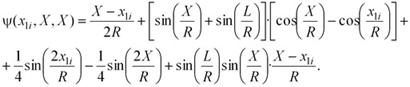
При Х = L, т.е. на конце рессоры, выражение (5) приобретает вид:
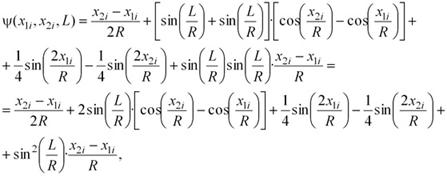
| . |
Рессора состоит из 6 стеклопластиковых листов, 5 листов межлистового полимерного материала-заполнителя и одного коренного стального листа, длина которого равна длине первого из ПКМ. Таким образом, по длине рессоры можно выделить 6 участков, разделенных следующим вектором граничных координат:
xГ = (0; 0,15; 0,235; 0,335; 0,43; 0,515; 0,63).
Тогда для прогиба произвольного сечения с координатой X получаем:
| , |
где xГ, N < X ≤ xГ, N+1.
При X = L:
| . |
Разделим суммарный прогиб δz на составляющие таким образом, что:
| , |
| . |
В соответствие с (3) получим:
| , |
где nKi, nPi, nCi — число листов ПКМ, полимера и стали в i-м сечении.
Для композиционного материала уравнение состояния имеет вид:
| (0 < α1 < 1). | (6) |
Для полимерного межлистового материала:
| (0 < α2 < 1). | (7) |
Для стали используем линейный закон Гука. Переходя к операторной форме, записываем для уравнений (6), (7) соотношения:
| (8) |
Используя переход, аналогичный (2)
| , |
|
имеем
| . |
Используя соотношения (8) получим:
| , |
| , |
| . |
И окончательно:
| , |
где
| , |
| , |
| , |
| , |
| , |
| , |
| , |
| , |
α1, τ1, θ1 — константы вязкоупругости ПКМ,
α2, τ2, θ2 — константы вязкоупругости полимерного межлистового материала,
A1...A2 — постоянные, задающие вязкоупругие свойства рессоры.
Получаем дифференциальное уравнение для силы на конце рессоры и компоненты прогиба:
| (9) |
Решение этого дифференциального уравнения даже при простом виде входных воздействий сопряжено с большими математическими трудностями, поэтому в работе предполагается решение его или в частотной области, или численно при имитационном моделировании.
Часть II. Частотные характеристики рессоры как упругодемпфирующего элемента
Для получения передаточной функции рассмотрим дифференциальное уравнение (9). Передаточную функцию рессоры как упругодемпфирующего элемента можно записать в виде:
| . | (10) |
АЧХ рессоры определим следующим образом:
| . |
График соответсвующей функции представлен на рисунке 2.
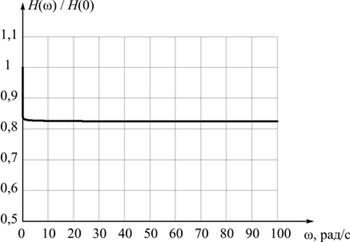
Рис. 2. АЧХ рессоры как упругодемпфирующего элемента
При часотах отличных от нулевой динамический отклик меньше статического, что обусловлено наличием демпфирования. Рессора с гистерезисным демпфированием при динамическом нагружении ведет себя как упругий элемент большей жесткости. При нулевой частоте (статическом нагружении) демпфирование тоже имеет место, однако при построении АЧХ рассматриваются исключительно установившиеся значения, а весь процесс проявления реономных свойств не учитывается.
Следует отметить особенность гистерезисного демпфирования как частотно-независимого вида трения, отраженную в [7]. При любой частоте величина демпфирования остается практически постоянной.
Для последующего анализа рессоры как упругодемпфирующего элемента построим простую механическую систему с вязкоупругой связью колеблющейся массы и источника возмущения, представленную на рисунке 3.

Рис. 3. Система с упругодемпфирующей связью
Дифференциальное уравнение, описывающее движение массы при кинематическом возмущении:
| , |
где P — действующая на массу упругодемпфирующая сила.
Переходя в частотную область:
|
где W = W(s) — передаточная функция упругодемпфирующего элемента, определнная по выржанию (10).
Учитывая, что прогиб упругодемпфирующего элемента определяется соотношением:
| , |
окончательно получим:
|
Откуда передаточная функция такой системы определится соотношением:
| . |
АЧХ механической системы, приведенной на рисунке 3, определяется соотношением
|
и приведено на рисунке 4 в сравнении с механической системой с линейно-вязким трением.
При расчете приняты следующие значения:
m = 500 кг,
c = 38470 Н/м — жесткость упругой связи для расчета линейной системы,
k = 2190 Н·с/м — коэффициент линейно-вязкого демпфирования, рассчитанный исходя из коэффициент относительного рассеяния энергии в механической системы ψ = 0,2.
Значение жесткости принято по мгновенной реакции рессоры.
Собственная частота консервативной системы составляет ωС ≈ 8,8 рад/с.
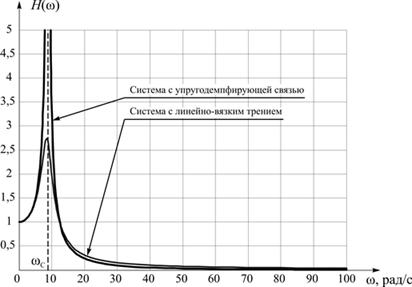
Рис. 4. АЧХ механических систем с гистерезисным и линейно-вязким трением
Анализ графиков показывает, что при гистерезисном демпфировании из-за методических ограничений кривая АЧХ имеет резонанс на собственной частоте. Амплитуда резонансных явлений в несколько раз больше, чем при линейном трении, что вызвано тем, что мера гистерезисного демпфирования меньше линейно-вязкого. Резонансная частота не смещаются с ростом частоты возмущения и изменении показателей демпфирования и равна собственной частоте консервативной системы. При линейно-вязком трении с ростом меры демпфирования собсвтенная частота колебаний уменьшается.
Часть III. Учет гистерезисного демпфирования при моделировании движения КМ в частотной области
Алгоритм расчета показателей плавности движения КМ и качества системы подрессоривания при плоской и пространственной схеме возмущения со стороны дороги подробно описан в [8, 9, 10].
Расматривается возможность замены линейных элементов систем подрессоривания на упругодемпфирующие. Возможность такого перехода рассмотрим на примере плоской схемы нагружения, описанной в [8, 9, 10].
Расчетная схема задачи приведена на рисунке 5.
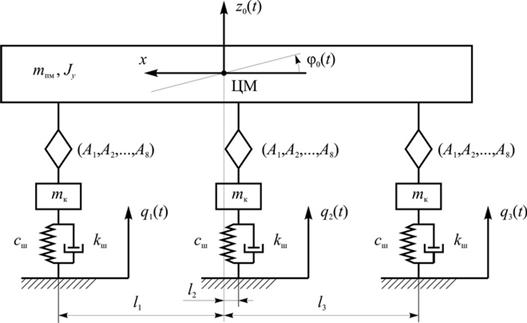
Рис. 5. Расчетная схема для системы с упругодемпфирующей связью колес с кузовом
Система дифференциальных уравнений, описывающих колебания масс системы:
| (11) |
где |
| —упругодемпфирующая сила в i-й рессоре. |
Применив к уравнениям системы (11) преобразование Лапласа, получим систему линейных уравнений:
|
Записывая для каждого упругодемпфирующего элемента соотношение
| , |
где | W(s) | — передаточная функция упругодемпфирующего элемента, определнная по выржанию (10), |
| —прогиб i-го упругодемпфирующего элемента, |
а для прогибов — выражение:
| , |
получим следующую систему линейных алгебраических уравнений относительно изображений по Лапласу обобщенных координат системы:
|
Для определения передаточных функций используется матричный метод решения систем линейных уравнений. Матрица системы M имеет вид:
|
где |
| . |
При этом вектор переменных, соотвествующих столбцам матрицы M имеет вид
(z0, φ0, z1, z2, z3).
Столбец свободных членов:
| , |
где |
| — передаточная функция упругодемпфирующего элемента, определнная по выржанию (10), |
|
| , |
| , | – времена запаздывания возмущений для средней и задней осей, |
V — скорость движения ВТС.
В статье оцениваются в качестве показателей плавности движения среднеквадратические отклонения вертикальных виброускорений кузова:
| , |
где Gq(ω) – спектральная плотность возмущения со стороны дороги,
| — АЧХ вертикальных виброускорений подрессоренной массы относительно возмущения. |
Часть IV. Определение показателей плавности движения и качества системы подрессоривания
Расчет производится аналитическим методом в трех дорожных условиях с соответствующими скоростями по предписанию ОСТ 37.001.275–84. Методика расчета подробно описана в [8, 9, 10]. Расчетные параметры нагрузочных режимов описаны [8, 10, 11]. Параметры жесткости и демпфирования разработанной модели рессоры определены экспериментально.
Объектом исследования в данной статье является ВТС «ЗЭТ 6х6» (рисунок 6), разработанное в конструкторском бюро кафедры «Колесные машины» МГТУ им. Н. Э. Баумана в 2007 году по заказу компании ОАО «АВТОРОС» (www.z-project.ru). Технические характеристики ВТС приведены в таблице 1.
Рис. 6. Вездеходное транспортное средство 6x6 со стеклопластиковой четверть-эллиптической рессорой
Таблица 1 — Технические характеристики ВТС «ЗЭТ 6x6»
╧ | Наименование показателя | Значение показателя |
1 | Полная масса, кг | 3500 |
2 | Неподрессоренная масса одного колеса, кг | 75 |
| Моменты инерции ВТС |
|
3 | относительно продольной оси КМ x, кг·м2 | 1010 |
4 | относительно поперечной оси КМ y, кг·м2 | 10012 |
5 | относительно вертикальной оси z, кг·м2 | 10310 |
6 | База, мм | 2375 |
7 | Ширина колеи, мм | 1890 |
8 | Расстояние от передней оси до центра масс ВТС, мм | 2328 |
9 | Полный ход подвески, мм | 300 |
| Шины «AVTOROS X-TRIM» |
|
10 | Наружный диаметр, мм | 1240 |
11 | Нормальная жёсткость шины, Н/м | 125020 |
Ниже представлены результаты решения поставленной задачи. В таблицах 2 – 4 приведены среднеквадратических отклонений вертикальных колебаний кузова при движении в различных дорожных условиях, а на рисунках 7 – 9 – графики среднеквадратических отклонений ускорений вертикальных колебаний кузова при движении в соответствующих дорожных условиях в одном из скоростных режимов.
Следует отметить, что при малых частотах в области 1 Гц при гистерезисном демпфировании возникает резонанс, обусловленный небольшой мерой гистерезисного демпфирования в резонансной области. Напротив, при больших частотах система с гистерезисным демпфированием оказывается наилучшей с точки зрения обеспечения требуемых показателей плавности движения.
Таблица 2 — Значения среднеквадратических отклонений вертикальных ускорений кузова при движении в дорожных условиях типа I
Частота, Гц | V = 30 км/ч | V = 50 км/ч | V = 70 км/ч | ||||||
1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |
0,80 | 0,2112 | 0,0629 | 0,0619 | 0,6860 | 0,1838 | 0,1803 | 1,0571 | 0,2773 | 0,2718 |
1,00 | 0,2033 | 0,0673 | 0,0615 | 0,8364 | 0,4435 | 0,3817 | 1,3458 | 0,7628 | 0,6524 |
1,25 | 0,0171 | 0,0711 | 0,0602 | 0,1428 | 0,6531 | 0,4856 | 0,2816 | 1,2828 | 0,9635 |
1,60 | 0,0329 | 0,0933 | 0,0931 | 0,0499 | 0,1552 | 0,1528 | 0,1470 | 0,4389 | 0,4348 |
2,00 | 0,0233 | 0,0553 | 0,0578 | 0,0116 | 0,0267 | 0,0281 | 0,0732 | 0,1740 | 0,1820 |
2,50 | 0,0203 | 0,0430 | 0,0467 | 0,0325 | 0,0697 | 0,0752 | 0,0225 | 0,0499 | 0,0535 |
3,15 | 0,0581 | 0,1218 | 0,1350 | 0,0336 | 0,0708 | 0,0782 | 0,0284 | 0,0591 | 0,0656 |
4,00 | 0,0514 | 0,1065 | 0,1202 | 0,0212 | 0,0434 | 0,0492 | 0,0505 | 0,1039 | 0,1176 |
5,00 | 0,0194 | 0,0371 | 0,0418 | 0,1013 | 0,1933 | 0,2182 | 0,0329 | 0,0656 | 0,0747 |
6,30 | 0,0675 | 0,1121 | 0,1200 | 0,1479 | 0,2504 | 0,2729 | 0,1161 | 0,1932 | 0,2072 |
8,00 | 0,0491 | 0,0955 | 0,1024 | 0,0335 | 0,0705 | 0,0770 | 0,1509 | 0,3430 | 0,3755 |
10,00 | 0,0149 | 0,0595 | 0,0755 | 0,0164 | 0,0653 | 0,0833 | 0,0407 | 0,1402 | 0,1680 |
12,50 | 0,0051 | 0,0263 | 0,0366 | 0,0166 | 0,0774 | 0,1043 | 0,0072 | 0,0346 | 0,0471 |
16,00 | 0,0039 | 0,0233 | 0,0336 | 0,0052 | 0,0337 | 0,0492 | 0,0113 | 0,0705 | 0,1023 |
20,00 | 0,0021 | 0,0158 | 0,0235 | 0,0033 | 0,0234 | 0,0347 | 0,0027 | 0,0198 | 0,0294 |
Графики среднеквадратических отклонений (СКО) вертикальных ускорений кузова представлены на рисунке 7. Цветом обозначены:
- черная кривая – нормативные значения виброускорений,
- синяя кривая – СКО виброускорений системы с гистрезисным демпфированием,
- зеленая кривая – СКО виброускорений системы с линейным показателем трения, той же меры, что и гистерезисное,
- красная кривая – СКО виброускорений системы с оптимальным значением линейно-вязкого трения.

Рис. 7. Графики среднеквадратических отклонений вертикальных виброускорений кузова при движении по дороге типа I со скоростью V = 50 км/ч
Таблица 3 — Значения среднеквадратических отклонений вертикальных ускорений кузова при движении в дорожных условиях типа II
Частота, Гц | V = 30 км/ч | V = 45 км/ч | V = 60 км/ч | ||||||
1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |
0,80 | 0,5623 | 0,1650 | 0,1623 | 1,3399 | 0,3557 | 0,3489 | 1,8001 | 0,4659 | 0,4567 |
1,00 | 0,5542 | 0,1865 | 0,1704 | 1,6569 | 0,8836 | 0,7609 | 2,3506 | 1,3692 | 1,1692 |
1,25 | 0,0501 | 0,2077 | 0,1763 | 0,2751 | 1,2624 | 0,9351 | 0,5138 | 2,3451 | 1,7618 |
1,60 | 0,0984 | 0,2791 | 0,2787 | 0,0737 | 0,2368 | 0,2323 | 0,2570 | 0,7737 | 0,7659 |
2,00 | 0,0711 | 0,1686 | 0,1760 | 0,0599 | 0,1352 | 0,1420 | 0,0988 | 0,2380 | 0,2488 |
2,50 | 0,0630 | 0,1338 | 0,1450 | 0,1052 | 0,2269 | 0,2444 | 0,0477 | 0,1011 | 0,1094 |
3,15 | 0,1819 | 0,3809 | 0,4223 | 0,0656 | 0,1387 | 0,1527 | 0,1194 | 0,2501 | 0,2771 |
4,00 | 0,1615 | 0,3345 | 0,3776 | 0,1352 | 0,2763 | 0,3137 | 0,1092 | 0,2260 | 0,2553 |
5,00 | 0,0612 | 0,1170 | 0,1321 | 0,3458 | 0,6669 | 0,7540 | 0,1440 | 0,2692 | 0,3024 |
6,30 | 0,2136 | 0,3547 | 0,3798 | 0,2747 | 0,4734 | 0,5203 | 0,5558 | 0,9295 | 1,0038 |
8,00 | 0,1553 | 0,3024 | 0,3241 | 0,0792 | 0,1798 | 0,1956 | 0,3825 | 0,7948 | 0,8579 |
10,00 | 0,0474 | 0,1887 | 0,2395 | 0,0859 | 0,3359 | 0,4233 | 0,0357 | 0,1385 | 0,1742 |
12,50 | 0,0163 | 0,0835 | 0,1160 | 0,0240 | 0,1107 | 0,1484 | 0,0399 | 0,2075 | 0,2893 |
16,00 | 0,0123 | 0,0740 | 0,1067 | 0,0207 | 0,1263 | 0,1825 | 0,0270 | 0,1556 | 0,2225 |
20,00 | 0,0066 | 0,0501 | 0,0747 | 0,0095 | 0,0758 | 0,1136 | 0,0140 | 0,1117 | 0,1675 |
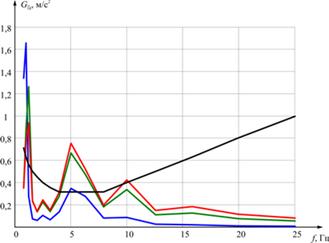
Рис. 8. Графики среднеквадратических отклонений вертикальных виброускорений кузова при движении по дороге типа II со скоростью V = 45 км/ч
Таблица 4 — Значения среднеквадратических отклонений вертикальных ускорений кузова при движении в дорожных условиях типа III
Частота, Гц | V = 10 км/ч | V = 12 км/ч | V = 15 км/ч | ||||||
1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |
0,80 | 0,9012 | 0,1667 | 0,1616 | 0,3041 | 0,0955 | 0,0940 | 0,5114 | 0,1237 | 0,1210 |
1,00 | 1,9343 | 1,2220 | 1,0403 | 0,5454 | 1,0266 | 0,8263 | 0,6802 | 0,3096 | 0,2737 |
1,25 | 0,3923 | 1,7903 | 1,3099 | 0,5899 | 2,6810 | 2,0124 | 0,3185 | 1,2904 | 1,1209 |
1,60 | 0,0621 | 0,1929 | 0,1889 | 0,2504 | 0,7727 | 0,7582 | 0,4707 | 1,3794 | 1,3668 |
2,00 | 0,0654 | 0,1483 | 0,1563 | 0,0450 | 0,1035 | 0,1088 | 0,2256 | 0,5378 | 0,5604 |
2,50 | 0,0944 | 0,2060 | 0,2205 | 0,0939 | 0,2003 | 0,2171 | 0,0484 | 0,1040 | 0,1124 |
3,15 | 0,0645 | 0,1347 | 0,1500 | 0,0818 | 0,1726 | 0,1897 | 0,1139 | 0,2379 | 0,2649 |
4,00 | 0,0537 | 0,1113 | 0,1254 | 0,0927 | 0,1902 | 0,2159 | 0,0968 | 0,2009 | 0,2263 |
5,00 | 0,0738 | 0,1466 | 0,1666 | 0,0812 | 0,1522 | 0,1711 | 0,1385 | 0,2639 | 0,2978 |
6,30 | 0,1083 | 0,1865 | 0,2031 | 0,1192 | 0,2052 | 0,2227 | 0,1318 | 0,2220 | 0,2377 |
8,00 | 0,0644 | 0,1428 | 0,1559 | 0,0805 | 0,1802 | 0,1980 | 0,1037 | 0,2270 | 0,2502 |
10,00 | 0,0268 | 0,0980 | 0,1204 | 0,0277 | 0,1051 | 0,1309 | 0,0365 | 0,1350 | 0,1672 |
12,50 | 0,0122 | 0,0592 | 0,0808 | 0,0148 | 0,0711 | 0,0969 | 0,0168 | 0,0828 | 0,1137 |
16,00 | 0,0061 | 0,0372 | 0,0538 | 0,0071 | 0,0429 | 0,0619 | 0,0093 | 0,0565 | 0,0818 |
20,00 | 0,0034 | 0,0262 | 0,0391 | 0,0044 | 0,0329 | 0,0490 | 0,0048 | 0,0368 | 0,0549 |

Рис. 9. Графики среднеквадратических отклонений вертикальных виброускорений кузова при движении по дороге типа III со скоростью V = 10 м/ч
Выводы
В рамках проведенного исследования разработана математическая модель механического поведения рессоры. Модель отличается универсальностью, позволяющей производить расчеты не только монолистовых рессор, но и учитывать структурную неоднородность рессоры по материалам. Модель разработана для рессоры, состоящей из листов трех различных материалов. Разработанная модель используют математический аппарат диффер-интегрирования дробного порядка.
Произведен анализ полученного дифференциального уравнения и сравнение поведения рессоры с поведением динамической системы с линейно-вязким трением, которое показывает частотную независимость гистерезисного демпфирования.
Разработан алгоритм расчета колебаний КМ в частотной области с учетом вязкоупругих свойств элементов систем подрессоривания, замещающих линейные элементы жесткости и линейно-вязкие демпферы. Определенные в результате расчета показатели плавности движения показывают, что только в самых нагруженных дорожных условиях при самых низких частотах наблюдается выход показателей плавности движения за предельно-допустимый уровень, что связано с методической погрешностью моделирования поведения рессоры при низких частотах, что показано на графике АЧХ упругодемпфирующего элемента.
Следующим этапом работы в данном направлении станет разработка имитационной модели для более достоверного описания поведения рессоры под нагрузкой с помощью численного интегрирования дробно-дифференциального уравнения (9).
Библиографический список:
- Афанасьев, Б.А. Проектирование элементов подсистем автомобиля из композиционных материалов / Б.А. Афанасьев, И.З. Даштиев. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2007. – 136 с.
- Тимофеева С.Д. Полимерные композиционные материалы в автомобилестроении (обзор) // Пластические массы. – 1990. – ╧9. – С. 78-87.
- Учайкин В.В. Метод дробных производных / В.В. Учайкин. – Ульяновск: Артишок, 2008. – 512 с.
- Kelly, Piaras. Solid Mechanics Lecture Notes. Reological Models: [Электронный ресурс]. URL: http://www3.esc.auckland.ac.nz/people/staff/pkel015/SolidMechanicsBooks/Part_I/BookSM_Part_I/07_Viscoelasticity/PDF/Viscoelasticity_03_Rheological.pdf. (Дата обращения: 12.06.2011).
- Mainardi Francesco, Gorenflo Rudolf. Time-fractional derivatives in relaxation processes: a tutorial survey // Fractional Calculus and Applied Analysis. – 2008. – ╧ 10, сб. 3. – С. 269-308.
- Shahsavari Rouzbeh, Ulm Franz-Josef. Indentation analysis of fractional viscoelastic solids // Journal of Mechanics of materials and Structures. – 2009. – ╧ 4. – C. 523-550.
- Демпфирование колебаний / А. Нашиф, Д. Джоунс, Дж. Хендерсон; пер. с англ. Л.Г. Корнейчука; под ред. Э. И. Григолюка. – М.: Мир, 1988. – 448 с.
- Жеглов Л. Ф. Спектральный метод расчета систем подрессоривания колесных машин: учеб. пособие / Л Ф. Жеглов. – М.: Изд-во МГТУ им. Н.Э. Баумана. 2009.– 150 с.
- Проектирование полноприводных колесных машин: в 3-х кн. / под ред. А.А. Полунгяна. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2008. – Т.3. – 2008. – 432 с.
- Ларин В.В. Теория движения колесных машин – М.: Изд-во МГТУ им. Н.Э. Баумана, 2010. – 391 с.
- Проектирование полноприводных колесных машин: в 3-х кн. / под ред. А.А. Полунгяна. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2008. – Т.1. – 2008. – 496 с.
Публикации с ключевыми словами: полимерные композиционные материалы, листовые рессоры, вязкоупругость, производные дробного порядка, плавность движения
Публикации со словами: полимерные композиционные материалы, листовые рессоры, вязкоупругость, производные дробного порядка, плавность движения
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||