научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 06, июнь 2011
УДК 330.131.7
Московская академия экономики и права (МАЭП)
В литературе определено следующее понятие «эффективности» [1] применительно к страховому процессу. «Эффективность» страхования – это ситуация, когда обе участвующие в процессе стороны – страхователь и страховщик – получают экономическую выгоду от заключения страхового договора по сравнению с ситуацией, когда такой договор не был заключен.
Рассмотрим основные подходы к оценке эффективности методов управления риском и оценке эффективности страхования производственно-хозяйственной деятельности промышленных предприятий на примере взаимосвязи моделей страхового риска и страховой сделки.
Допустим, что страховщик и страхователь заключили договор страхования, который является юридическим оформлением факта страховой сделки. После того, как договор вступит в силу, отношения страховщика и страхователя могут развиваться двумя путями в зависимости от наступления или не наступления страхового случая. Если за период действия договора страховой случай не наступает, то страховщик приобретает, а клиент теряет страховой взнос. При наступлении страхового случая страховщик теряет, а страхователь приобретает страховое возмещение. Адекватной данному описанию математической моделью сделки является совокупность двух случайных величин следующего вида:
1) исход сделки для страховщика:
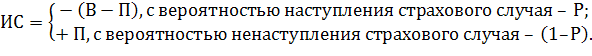
2) исход сделки для страхователя:

Где, П – сумма страховой премии, В – сумма страхового возмещения, P – вероятность наступления страхового случая.
Для данной модели страховой сделки по страхованию рисков производственно-хозяйственной деятельности, ожидаемые результаты для участников интерпретируются следующим образом [2]:
Таблица 1
Результаты сделки страховщика и страхователя
Результаты сделки | Страховщик | Страхователь |
Ожидаемый доход от сделки Ожидаемый расход от сделки | П х (1 – Р) – (В – П) х Р | (В – П) х Р – П х (1 – Р) |
Баланс интересов страховщика и страхователя имеет место при равенстве ожидаемых доходов и потерь от сделки:
П х (1 – P ) = ( В – П ) х Р, откуда следует Р = В / П.
Предположим теперь, что величина страхового возмещения принимается равной произведению страховой стоимости (С) объекта страхования на величину математического ожидания относительно невыполнения обязательств по договору (MU) при наступлении страхового случая. Тогда имеем:
В = С х MU и П = С х MU х Р.
Если теперь положить С = 1, то получаем описание модели сделки через параметры страхового риска:
1) исход сделки для страховщика:

2) исход сделки для страхователя:

Для этой модели ожидаемые доходы и убытки партнеров по сделке определяются по формулам:
Таблица 2
Ожидаемые доходы и убытки партнеров по сделке
Результаты сделки | Страховщик | Страхователь |
Ожидаемый доход от сделки Ожидаемый расход от сделки | MU х P х (1 – Р) – MU х P х (1 – P) | MU х P х (1 – P) – MU х P х (1 – Р) |
Отсюда предположим, что вероятность наступления страхового случая (Р) равна 30 %, а величина математического ожидания относительного относительно невыполнения обязательств по договору (MU) равна 60%.
Подставив значения в формулу получим, что ожидаемый доход от сделки для страховщика составит:
0,6 х 0,3 х (1 – 0,3) = 0,18 х 0,7 = 0,126 = 12,6 %,
а, соответственно, ожидаемый расход страхователя от сделки составит:
– 0,6 х 0,3 х (1 – 0,3) = – 0,18 х 0,7 = – 0,126 = – 12,6 %.
Что касается обратному исходу сделки, то вычисления будут обратные.
Процедура моделирования процесса страхования
При страховании предпринимательских рисков производственно-хозяйственной деятельности промышленного предприятия в экономические отношения вступают два субъекта: страхователь (в лице промышленного предприятия) и страховщик (профессиональная страховая организация). Рассмотрим специфику поведения и цели каждого из них при заключении договора страхования.
Предположим, промышленное предприятие планирует заключить договор страхования своих финансовых инвестиций. Целью такого страхования является защита инвестиционных вложений от возможных потерь, возникающих вследствие неблагоприятного, непредсказуемого изменения конъюнктуры рынка, а также ухудшения иных условий для эффективного осуществления инвестиционной деятельности. Характер деятельности промышленного предприятия определяет и характер подлежащих страхованию рисков – в данном случае производится страхование от коммерческих рисков (при осуществлении инвестиций внутри страны).
Обозначим: p – вероятность наступления страхового случая (таковыми здесь являются возможные потери инвестора, а также неполучение им намеченной прибыли в результате оговоренных событий), b – сумма страхового взноса, уплачиваемая страхователем в определенном порядке, C – страховая сумма, в пределах которой страховщик обязуется выплатить страхователю при наступлении страхового случая, причем величина C не превышает суммы величины страхуемых инвестиций и оговоренного объема прибыли.
Ожидаемый выигрыш страховой компании складывается из двух частей:
1) при наступлении страхового случая страховщик выплачивает сумму страхового возмещения, получив лишь сумму страхового взноса;
В этом случае ее выигрыш будет отрицательным и составит ![]() (здесь мера риска равна произведению суммы ожидаемого ущерба на вероятность того, что ущерб произойдет).
(здесь мера риска равна произведению суммы ожидаемого ущерба на вероятность того, что ущерб произойдет).
2) если страхового случая за весь период действия договора страхования не произойдет, страховая компания получает чистый положительный выигрыш за счет уплаченной страхователем страховой премии, который составит ![]() .
.
Очевидно, что страховая компания пойдет на риск заключения договора страхования лишь в том случае, если общая сумма ее выигрыша окажется положительной:
![]() .
.
После несложных преобразований получим: ![]() . Последнее и есть условие заключения договора страховой компанией. Однако чтобы установить соотношение между b и C необходимо обладать статистическими данными об имевших место потерях (убытках и неполученной прибыли) при осуществлении инвестиционной деятельности.
. Последнее и есть условие заключения договора страховой компанией. Однако чтобы установить соотношение между b и C необходимо обладать статистическими данными об имевших место потерях (убытках и неполученной прибыли) при осуществлении инвестиционной деятельности.
Для страхователя же является актуальным вопрос, в каких случаях стоит рисковать своими средствами в размере уплачиваемой страховой премии, а в каких – нет.
Ожидаемый выигрыш страхователя также складывается из двух частей:
![]() ,
,
или после преобразований:
![]() .
.
Как было сказано выше, страховщик заключает договор страхования в том случае, если ![]() , или, что то же самое, если
, или, что то же самое, если ![]() . Это означает, что ожидаемая сумма выигрыша страхователя всегда будет отрицательна. Отсюда возникает закономерный вопрос – так выгодное ли это дело страхование (с точки зрения потенциального страхователя)? Страховать (заключать договор страхования и уплачивать страховую премию в пользу страховщика) или не страховать?
. Это означает, что ожидаемая сумма выигрыша страхователя всегда будет отрицательна. Отсюда возникает закономерный вопрос – так выгодное ли это дело страхование (с точки зрения потенциального страхователя)? Страховать (заключать договор страхования и уплачивать страховую премию в пользу страховщика) или не страховать?
Дело в том, что страхователь должен оценивать не просто ожидаемую величину выигрыша, а ее полезность. Иными словами, жертва (в данном случае – сумма уплачиваемой страховой премии) оправдана, если рискуя только этими средствами страхователь избегает очевидно больших потерь.
Рассмотрим задачу принятия решения при различных функциях полезности.
1) При пропорциональном (нейтральном) отношении полезность общего результата равна ![]() . Эта сумма будет положительной, если
. Эта сумма будет положительной, если ![]() , т. е.
, т. е. ![]() . Последнее противоречит условию страхования со стороны страховщика (
. Последнее противоречит условию страхования со стороны страховщика (![]() ), а следовательно можно утверждать, что при нейтральном отношении страхование производиться не будет.
), а следовательно можно утверждать, что при нейтральном отношении страхование производиться не будет.
2) При осторожном отношении полезность общего результата равна:
![]() .
.
Условие ![]() требует, чтобы
требует, чтобы ![]() . После некоторых преобразований из последнего выражения следует условие страхования при осторожном отношении:
. После некоторых преобразований из последнего выражения следует условие страхования при осторожном отношении:
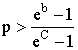 .
.
Для наглядного представления действий страхователя при осторожном отношении построим следующий график (cм. рисунок) [3]. По оси абсцисс откладываются значения страховых взносов b в условных единицах (от 0 до 1), а по оси ординат – масштаб значений вероятностей наступления страхового случая p (также, от 0 до 1). Принимая страховую сумму C = 1, рассчитаем граничные значения вероятностей p, соответствующие:
· условию страхования при осторожном отношении:
 ,
,
· требованию страховщика:
![]()
(это следует из ![]() ).
).
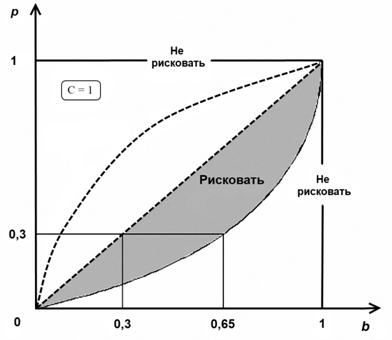
Первому из этих выражений соответствует сплошная линия на графике, второму – пунктирная. Заключенная между этими линиями заштрихованная часть графика представляет собой область, соответствующую решению страхователя при осторожном отношении идти на риск заключения договора страхования. Действительно, для любой из точек этой области справедливы и условие страхования при осторожном отношении, и требование страховщика. График наглядно показывает, что решение о страховании будет приниматься страхователем не во всех случаях.
Так, например, при вероятности наступления страхового случая равной 0,3, финансовые инвестиции будут подлежать страхованию лишь в том случае, если сумма страхового взноса будет составлять от 0,3 до 0,65 условной единицы.
При смелом отношении решение пойти на риск страхования принимается, если:
![]() .
.
Путем преобразований получим условие страхования при смелом отношении:
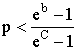 .
.
Построим на графике (рисунок) предельную кривую, соответствующую страхованию при смелом отношении:
 .
.
Эта кривая, показанная на графике прерывистой линией, проходит слева от линии требования страховщика, т.е. в области, где страхование нецелесообразно для страховой компании. Интересы страхователя и страховщика никогда не совпадают, следовательно, страхование при смелом отношении не состоится.
Данная математическая модель исследует возможные варианты организации процесса страхования и показывает, что страхователь и страховщик придут к взаимному согласию и подписанию договора страхования только в случае, когда интересы каждой из сторон будут учтены, т.е. с позиции страхователя оценивается выигрыш в виде полезности конкретного договора страхования, а с позиции страховой компании – получение прибыли за счет назначения адекватной цены страхования с учетом вероятностей возникновения рисковых ситуаций.
Кроме того, для облегчения процедуры соглашения «страхователь-страховщик» и, соответственно, повышения эффективности управления рисками по мнению автора были бы уместны следующие действия:
· предусмотреть создание отдельного законодательного акта, либо внести необходимые изменения и дополнения в действующий закон «Об организации страхового дела» [4] для обеспечения равноправной конкуренции и соблюдения антимонопольного законодательства, для частных страховых компаний;
· установить ограничение по деятельности страховому агентству, в случае наличия задолженности перед бюджетом государства и других коммерческих структур;
· оказывать помощь промышленным предприятиям в финансировании, страховании в качестве государственных субсидий и гарантий, что будет способствовать росту товарооборота между Россией и другими странами.
Список литературы
1. Гвозденко, А.А. Страхование: учеб. – М.: ТК Велби, Изд-во Проспект, 2006.
2. Балабанов И. Т. Риск-менеджмент. – М.: Финансы и статистика. – 2006. – с. 192.
3. Извеков Д.В. Система страхования рисков производственно-хозяйственной деятельности промышленного предприятия. Дисс. … канд. экон. наук: 08.00.05. – М.: РГГУ. 2009. – с. 99.
4. «Об организации страхового дела в Российской Федерации» Закон РФ от 29 ноября 2007 г. ╧ 4015-I.
Публикации с ключевыми словами: эффективность, оценка эффективности, страхование риска, процесс страхования, управление риском, страховой случай
Публикации со словами: эффективность, оценка эффективности, страхование риска, процесс страхования, управление риском, страховой случай
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



