научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 06, июнь 2011
УДК 004
УДК 004.3 + 519.6
МГТУ им. Н.Э. Баумана
В ходе реализации алгоритмов над графами неоднократно приходится выполнять над представляющими их множествами операции пересечения, объединения, дополнения и др. Асимптотическая оценка вычислительной сложности «в худшем» этих операций над неупорядоченными множествами X и Y равна O(n×m), где n = | X |, m = |Y |. В [1] показано, что операции пересечения, объединения и дополнения над упорядоченными множествами требуют меньшего количества операций сравнения, что позволит снизить вычислительную сложность алгоритмов. Однако остальные операции там исследованы не были.
Будем считать, что множества заданы перечислением элементов, а элементы представлены их номерами в универсуме. Упорядочивание множеств в данном случае рассматривается как сортировка номеров, т. е. целых чисел, например по их возрастанию. Для сравнения эффективности операций над неупорядоченными и упорядоченными множествами будем оценивать их вычислительную сложность по количеству сравнений элементов множеств. Проверку условий выхода из циклов учитывать не будем.
Рассмотрим особенности реализации операций над упорядоченными множествами. Упорядоченность элементов множеств X и Y позволит нам в общем случае исключать сравнение их индексов, лежащих в определенных диапазонах. Например, если при проверке условия xi = yj выяснится, что x1 не равно и больше y8, то все следующие элементы множества Х нет необходимости сравнивать с y1, y2,…, y8. Напомним, что для реализации операций пересечения, объединения и дополнения над неупорядоченными множествами в худшем случае требуется сравнение каждого элемента со всеми.
Для получения объективной оценки сверху вычислительной сложности операций над упорядоченными множествами необходимо определить, какие операции отношения номеров следует выполнять, и сконструировать такие наборы данных, которые потребуют максимального числа проверок. Вид операций над номерами и их количество зависят от типа операции над множествами и соотношения целых констант, задающих элементы xi ![]() X и xj
X и xj ![]() Y. Таким образом, конструирование наборов данных заключается в определении соотношения элементов двух массивов.
Y. Таким образом, конструирование наборов данных заключается в определении соотношения элементов двух массивов.
Отметим важный факт – множество, полученное в результате выполнения любой операции над упорядоченными множествами, является упорядоченным.
Принадлежность элемента упорядоченному множеству. При поиске y = xi в упорядоченном множестве методом двоичного деления меньшее количество операций сравнения будет, если проверять данное условие (или инверсное y ![]() xi), и при его невыполнении (для инверсного при выполнении) проверять условие y > xi либо y < xi. Количество операций сравнения будет максимальным, если y
xi), и при его невыполнении (для инверсного при выполнении) проверять условие y > xi либо y < xi. Количество операций сравнения будет максимальным, если y ![]() Х, и равно:
Х, и равно:
Nср. пр = 2 log2n,
где n = |X|.
Алгоритм выполнения этой операции показан на рис.1.

Рис. 1. Схема алгоритма выполнения операции принадлежности элемента упорядоченному множеству
Считая, что cортировка массива, состоящего из n элементов, требует n log2n операций сравнения, получим суммарное количество сравнений, необходимых для предварительного упорядочивания множеств и выполнения операции y ![]() Х:
Х:
![]() = (n + 2) log2n.
= (n + 2) log2n.
Таким образом, асимптотическая оценка вычислительной сложности выполнения операции y ![]() Х над упорядоченным множеством с учётом вычислительной сложности сортировки O(n log2n). Очевидно, что использование упорядоченного множества при однократном выполнении операции y
Х над упорядоченным множеством с учётом вычислительной сложности сортировки O(n log2n). Очевидно, что использование упорядоченного множества при однократном выполнении операции y ![]() Х и отсутствии других операций над этим множеством нецелесообразно. Степень сокращения количества сравнений за счёт упорядочивания, например при n-кратном выполнении этой операции, будет:
Х и отсутствии других операций над этим множеством нецелесообразно. Степень сокращения количества сравнений за счёт упорядочивания, например при n-кратном выполнении этой операции, будет:
K = n2 / 3n log2n = n / 3 log2n.
Реализация операции проверки включения упорядоченных множеств X ![]() Y. Из определения операции следует, что отношение нестрогого включения не выполняется, если хотя бы для одного элемента xi
Y. Из определения операции следует, что отношение нестрогого включения не выполняется, если хотя бы для одного элемента xi ![]() Х не существует yj такого, что xi = yj. При сравнении элементов упорядоченных по возрастанию множеств справедливость xi
Х не существует yj такого, что xi = yj. При сравнении элементов упорядоченных по возрастанию множеств справедливость xi ![]() yj и xi < yj означает, что никакой элемент множества Y не равен xi. Поскольку возможен вариант, когда Х \ xn
yj и xi < yj означает, что никакой элемент множества Y не равен xi. Поскольку возможен вариант, когда Х \ xn ![]() Y и xn = ym, условием продолжения сравнения элементов множеств Х и Y будет:
Y и xn = ym, условием продолжения сравнения элементов множеств Х и Y будет:
i ![]() n & j
n & j ![]() m & r = 0,
m & r = 0,
где r = 0 – признак того, что ситуация xi ![]() yj и xi < yj не имела места.
yj и xi < yj не имела места.
При выполнении условия xi = yj необходимо переходить к сравнению следующих элементов рассматриваемых множеств. Алгоритм установления справедливости отношение нестрогого включения множеств Х и Y показан на рис. 2.
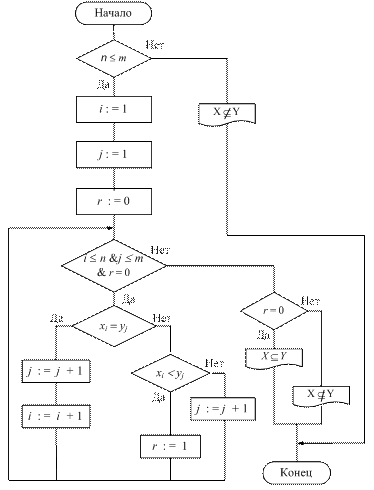
Рис. 2. Схема алгоритма выполнения операции нестрогого включения упорядоченных множеств
Вариантом исходных данных, при котором количество операций сравнения элементов множеств максимально, будет например такой, при котором
ym–1 < x1 & x1 ![]() ym.
ym.
Максимальное количество операций сравнения (оценка в худшем) определяется по формуле
Nср. вкл = 2 m.
Суммарное количество сравнений, требуемых для предварительного упорядочивания множеств и выполнения операции Х ![]() Y:
Y:
![]() = n×log2n + m (log2m + 2).
= n×log2n + m (log2m + 2).
Отсюда, количество операций сравнения, необходимых для выполнения операции Х ![]() Y, сократится за счет упорядочивания в
Y, сократится за счет упорядочивания в
K = n m / (n×log2n + m (log2m + 2))
раз. При достаточно большом m (m >> n)
K = n / log2m.
Реализация операций отношения строгого включения и равенства упорядоченных множеств X ![]() Y и X = Y. Алгоритмы выполнения этих операций над упорядоченными множествами аналогичны алгоритму операции Х
Y и X = Y. Алгоритмы выполнения этих операций над упорядоченными множествами аналогичны алгоритму операции Х ![]() Y. Очевидно, что вначале необходимо проверять условие n < m и n = m соответственно.
Y. Очевидно, что вначале необходимо проверять условие n < m и n = m соответственно.
Реализация операции объединения упорядоченных множеств Z = X ![]() Y. В соответствии с определением операции в ходе сравнения элементов множеств Х и Y нам надо записывать в множество Z различные элементы из того и другого множеств, а если элементы совпадают, то записывать один из них. Однако при сопоставлении двух элементов упорядоченных множеств установление факта, что xi
Y. В соответствии с определением операции в ходе сравнения элементов множеств Х и Y нам надо записывать в множество Z различные элементы из того и другого множеств, а если элементы совпадают, то записывать один из них. Однако при сопоставлении двух элементов упорядоченных множеств установление факта, что xi ![]() yj, является необходимым, но не достаточным основанием для занесения xi
yj, является необходимым, но не достаточным основанием для занесения xi ![]() X или yj
X или yj ![]() Y в множество Z. При упорядочивании по возрастанию элемент xi следует заносить в множество Z, если xi < yj, а элемент yj – при yj
Y в множество Z. При упорядочивании по возрастанию элемент xi следует заносить в множество Z, если xi < yj, а элемент yj – при yj ![]() xi(или xi при xi
xi(или xi при xi ![]() yj, а yj – при yj < xi). Следовательно, кроме отношения равенства нам необходимо проверять и отношение «меньше».
yj, а yj – при yj < xi). Следовательно, кроме отношения равенства нам необходимо проверять и отношение «меньше».
При выполнении условия xi > yj следует переходить к сравнению xi с yj+1. Однако, если для некоторого xi справедливо xi > ym, это означает, что все элементы xi+1, xi+1,…, xn > ym. Для обнаружения этой ситуации и выполнения соответствующих операций после выхода из цикла сравнения элементов множеств X и Y необходимо проверять условие i ![]() n. При выполнении данного условия в множество Z следует записать все оставшиеся элементы множества X, начиная с xi. Аналогично возможна ситуация, когда yj > xn. Следовательно, необходимо также проверять условие j
n. При выполнении данного условия в множество Z следует записать все оставшиеся элементы множества X, начиная с xi. Аналогично возможна ситуация, когда yj > xn. Следовательно, необходимо также проверять условие j ![]() m и при его выполнении в множество Z записывать оставшиеся элементы множества Y, начиная с yj. На рис. 3 показан алгоритм выполнения операции объединения упорядоченных множеств X и Y.
m и при его выполнении в множество Z записывать оставшиеся элементы множества Y, начиная с yj. На рис. 3 показан алгоритм выполнения операции объединения упорядоченных множеств X и Y.

Рис. 3. Схема алгоритма выполнения операции объединения упорядоченных множеств
Обратимся теперь к задаче конструирования худшего варианта данных. При m > n количество операций сравнения будет наибольшим, если 1-й элемент множества X придётся сравнивать со всеми элементами множества Y, а остальные элементы x2, x3,…, xn с элементом ym. Т.е. худший вариант данных должен удовлетворять условию:
(ym–1 < xi < ym) & (xn ![]() ym), i = 1, n – 1. (1)
ym), i = 1, n – 1. (1)
Нетрудно видеть, что максимальное количество операций сравнения (оценка в худшем) будет определяться по формуле
Nср. о = 2 (n + m – 1). (2)
При |X| = |Y| = n суммарное количество сравнений, требуемых для предварительного упорядочивания множеств и выполнения операции объединения:
![]() = 2n×log2n + 4n – 2.
= 2n×log2n + 4n – 2.
Отсюда, количество операций сравнения, необходимых для выполнения операции объединения, сократится за счет упорядочивания в
K = n2 / (2n×log2n + 4n – 2)
раз. При достаточно большом n
K = n / log2n (3).
Например, K = 102 при n = 1024 и k = 1170 при n = 16384.
Реальное сокращение количества операций будет более существенным, чем мы оценили по (3), если операция объединения (и другие, ей подобные) осуществляются в ходе работы алгоритма неоднократно.
Реализация операции пересечения упорядоченных множеств Z = X ![]() Y. По определению операции в множество Z следует записывать элемент xi или yj при выполнении условия xi = yj. Можно ли при сопоставлении элементов множеств X и ограничится проверкой условия xi = yj и переходить к сравнению следующей пары? Нет, этого достаточно только, если Х = Y, при этом получение Z потребует n операций сравнения, где n = |X| = |Y|. Таким образом, Nср.л.= n – это минимальное количество операций сравнения, т.е. оценка в лучшем. Давайте рассмотрим пример. Пусть X = <1, 3, 6> и Y = <2, 4, 5>. Выполнив сравнение xi = yj для первых элементов этих массивов, мы определили, что они не равны, следовательно никакой элемент из этой пары пока нельзя заносить в множество Z. Однако мы можем исключить из дальнейшего рассмотрения тот элемент, который имеет меньшее значение (большее, если бы множества были упорядочены по убыванию). Следовательно, кроме операции сравнения xi = yj необходимо проверять условие xi < yj. Таким образом, при каждом сравнении элементов нам в худшем случае придется проверять результаты двух операций xi = yj и xi < yj.
Y. По определению операции в множество Z следует записывать элемент xi или yj при выполнении условия xi = yj. Можно ли при сопоставлении элементов множеств X и ограничится проверкой условия xi = yj и переходить к сравнению следующей пары? Нет, этого достаточно только, если Х = Y, при этом получение Z потребует n операций сравнения, где n = |X| = |Y|. Таким образом, Nср.л.= n – это минимальное количество операций сравнения, т.е. оценка в лучшем. Давайте рассмотрим пример. Пусть X = <1, 3, 6> и Y = <2, 4, 5>. Выполнив сравнение xi = yj для первых элементов этих массивов, мы определили, что они не равны, следовательно никакой элемент из этой пары пока нельзя заносить в множество Z. Однако мы можем исключить из дальнейшего рассмотрения тот элемент, который имеет меньшее значение (большее, если бы множества были упорядочены по убыванию). Следовательно, кроме операции сравнения xi = yj необходимо проверять условие xi < yj. Таким образом, при каждом сравнении элементов нам в худшем случае придется проверять результаты двух операций xi = yj и xi < yj.
Схема алгоритма, основанного на изложенных соображениях, представлена на рис. 4.

Рис. 4. Схема алгоритма выполнения операции пересечения упорядоченных множеств
Ясно, что количество операций сравнения элементов будет максимальным, если множества X и Y не пересекаются (для общих элементов пересекающихся множеств проверка xi < yj не будет выполняться и два элемента – xi и yj будут исключены из рассмотрения). Учитывая, что Х и Y упорядоченные множества, максимальное количество операций сравнения будет, например при n < m, если выполняется условие (1). Нетрудно видеть, что максимальное количество операций сравнения (оценка в худшем) будет определяться по формуле (2).
Реализация операции относительного дополнения множества Y до X: Z = X \ Y. По определению операции в множество Z необходимо заносить те элементы множества X, которые не равны никакому элементу множества Y. Следовательно, алгоритм этой операции должен отличаться от алгоритма операции Z = X ![]() Y только тем, что в множество Z не следует записывать элементы множества Y (см. рис. 5).
Y только тем, что в множество Z не следует записывать элементы множества Y (см. рис. 5).

Рис. 5. Алгоритм выполнения операции дополнения упорядоченных множеств
Максимальное количество операций сравнения будет при выполнении условия (1) и оценивается по формуле (2).
Реализация операции симметрической разности упорядоченных множеств X и Y: Z = X ![]() Y. В соответствии с определением операции множество Z составляют те элементы xi
Y. В соответствии с определением операции множество Z составляют те элементы xi ![]() X и yj
X и yj ![]() Y, которые не равны друг другу. Очевидно, что алгоритм выполнения этой операции будет отличаться от алгоритма объединения множеств только тем, что при xi = yj не выполняется zk := yj. Алгоритм реализации операции Z = X
Y, которые не равны друг другу. Очевидно, что алгоритм выполнения этой операции будет отличаться от алгоритма объединения множеств только тем, что при xi = yj не выполняется zk := yj. Алгоритм реализации операции Z = X ![]() Y представлен на рис. 6.
Y представлен на рис. 6.
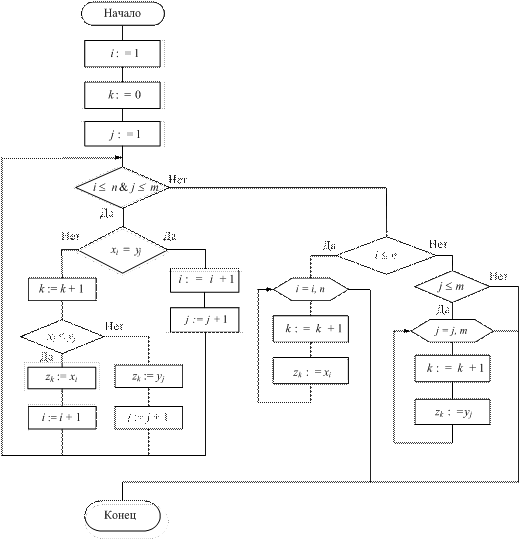
Рис. 6. Алгоритм выполнения операции симметрической разности упорядоченных множеств
Худший вариант исходных данных и вычислительная сложность те же, что и у предыдущей операции.
Литература
1. Овчинников В. А. Алгоритмизация комбинаторно-оптимизационных задач при проектировании ЭВМ и систем: Учеб. для вузов.– М.: Изд-во МГТУ им. Н. Э. Баумана, 2001. – 288с.
Публикации с ключевыми словами: операции, упорядоченные множества, вычислительная сложность
Публикации со словами: операции, упорядоченные множества, вычислительная сложность
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



