научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 06, июнь 2011
УДК 621.813, 621.815
МГТУ им. Н.Э.Баумана, г. Москва
Цикл статей посвящен разработке инженерной методики расчета соединения двух деталей с цилиндрическими сопрягаемыми поверхностями с малым радиальным зазором и различной жесткостью охватывающей детали. В первом случае, введя ориентировочную оценку по жесткости охватывающей детали, считаем последнюю безграничной в радиальном направлении. Для первого случая в работе / 1 / в общей постановке представлена методика определения формы и размеров эпюры контактного давления и построены графики для расчета этих параметров. Было установлено, что эпюра контактного давления в зависимости от угловой координаты изменяется по эллиптической зависимости. Данная статья является продолжением работы / 1 /.
Обычно прочность охватывающей детали с цилиндрическим отверстием ниже, чем прочность охватываемой цилиндрической детали, взаимодействующей с указанным отверстием. Цель данной статьи определение напряженно-деформированного состояния охватывающей детали.
Теоретические исследования проводились методами задачи плоской деформации теории упругости [2, 3].
2.3. Разложение эллиптической эпюры контактного давления в ряд Фурье.
На рис. 1 показана расчетная схема для определения напряженно-деформированного состояния охватывающей детали 2.
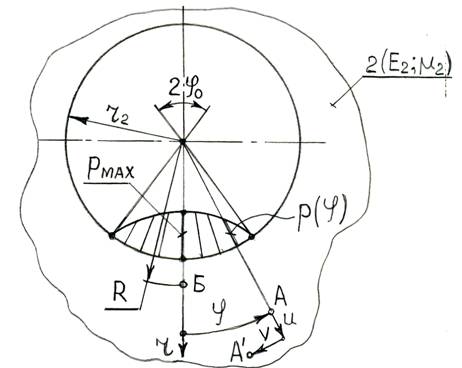
Рис. 1. Расчетная схема.
На этом рисунке:
![]() – радиус отверстия в охватывающей детали;
– радиус отверстия в охватывающей детали;
Е2 и ![]() – модуль упругости и коэффициент Пуассона охватывающей детали;
– модуль упругости и коэффициент Пуассона охватывающей детали;
![]() – контактное давление;
– контактное давление;
![]() – максимальное значение контактного давления;
– максимальное значение контактного давления;
![]() – полуугол контакта;
– полуугол контакта;
![]() и
и ![]() – полярные координаты.
– полярные координаты.
Для упрощения расчетов в работе / 1 / для определения контактного давления было принято допущение о том, что детали соединения с зазором металлические. Приняв ![]() , при определении контактного давления может получиться ошибка, которая не превышает одного процента. В данной статье можно учитывать реальное значение коэффициента Пуассона охватывающей детали.
, при определении контактного давления может получиться ошибка, которая не превышает одного процента. В данной статье можно учитывать реальное значение коэффициента Пуассона охватывающей детали.
Эпюра контактного давления (см. рис. 1) раскладывалась в ряд Фурье [4]

![]() , ( 1 )
, ( 1 )
где ![]() – функция Бесселя первого рода порядка 1 [5] определялась численно с помощью интегрального представления [6].
– функция Бесселя первого рода порядка 1 [5] определялась численно с помощью интегрального представления [6].
Число членов ряда Фурье выбиралось из условия, чтобы погрешность при разложении для любой угловой координаты ![]() (в том числе, при
(в том числе, при ![]() , где контактное давление равно нулю) не превышала 1 – 2% от рMAX.
, где контактное давление равно нулю) не превышала 1 – 2% от рMAX.
Для достижения указанной погрешности с уменьшением полуугла контакта ![]() число членов m ряда Фурье увеличивается. К примеру, для малых полууглов контакта
число членов m ряда Фурье увеличивается. К примеру, для малых полууглов контакта ![]() число членов m > 1000 … 2000. Объясняется это эффектом Гиббса [4], который проявляется на краях (ориентировочно для углов в диапазоне
число членов m > 1000 … 2000. Объясняется это эффектом Гиббса [4], который проявляется на краях (ориентировочно для углов в диапазоне ![]() ± 0,2×
± 0,2×![]() ) зоны контактного давления в скачкообразном увеличении разложенного в ряд давления. Для уменьшения числа членов m ряда Фурье использовался множитель Ланцоша [7], с помощью которого число членов удалось снизить на 30 – 40 %, но для малых углов
) зоны контактного давления в скачкообразном увеличении разложенного в ряд давления. Для уменьшения числа членов m ряда Фурье использовался множитель Ланцоша [7], с помощью которого число членов удалось снизить на 30 – 40 %, но для малых углов ![]() число членов m все равно превышало 1000.
число членов m все равно превышало 1000.
2.4. Исследование напряженного состояния охватывающей детали.
Для определения напряжений в полярных координатах выберем, удовлетворяющую бигармоническому уравнению, функцию напряжений Эри в следующем виде [2, 3]
![]()
![]() , (2)
, (2)
где: ![]() – произвольные постоянные, которые определяются из граничных условий.
– произвольные постоянные, которые определяются из граничных условий.
Компоненты напряжений определяются по следующим зависимостям
![]() ; (3)
; (3)
![]() ; (4)
; (4)
![]() (5)
(5)
Граничные условия: для ![]()
![]() ;
; ![]() .
.
для ![]()
![]() ;
; ![]() .
.
Функция Эри дифференцировалась по формулам (3) – (5), затем в полученные выражения подставлялись граничные условия, и после целого ряда преобразований получены следующие зависимости для определения компонентов напряжений
 (6)
(6)
 (7)
(7)
 (8)
(8)
![]() (9 )
(9 )
Анализ напряженного состояния охватывающей детали. Напряженное состояние этой детали определялось для полууглов контакта ![]() = 2°; 10°; 20°; 30°; 40°; 50° и 60°. Для общности результатов расчета вводились безразмерные параметры
= 2°; 10°; 20°; 30°; 40°; 50° и 60°. Для общности результатов расчета вводились безразмерные параметры ![]() и
и ![]() . Безразмерный параметр
. Безразмерный параметр![]() характеризует эквивалентные напряжения, а ρ является безразмерным радиусом. Диапазон изменения безразмерного радиуса ρ составляет от 1 для
характеризует эквивалентные напряжения, а ρ является безразмерным радиусом. Диапазон изменения безразмерного радиуса ρ составляет от 1 для ![]() до 0 для
до 0 для ![]() .
.
Используя гипотезу наибольших касательных напряжений [8], определялось напряженное состояние в точках охватывающей детали. Как показал анализ, точка «Б», в которой действует наибольшее значение эквивалентных напряжений sМАХ, располагается в общем случае в глубине детали под максимальным контактным давлением (при ![]() = 0) на некотором радиусе R, см. рис. 1. Для больших полууглов контакта
= 0) на некотором радиусе R, см. рис. 1. Для больших полууглов контакта ![]() указанный радиус
указанный радиус ![]() , то есть точка «Б», в которой действует наибольшее эквивалентное напряжение sМАХ, располагается на поверхности отверстия охватывающей детали.
, то есть точка «Б», в которой действует наибольшее эквивалентное напряжение sМАХ, располагается на поверхности отверстия охватывающей детали.
На рис. 2 показаны графики зависимости безразмерных эквивалентных напряжений ![]() от безразмерного радиуса
от безразмерного радиуса ![]() вдоль оси
вдоль оси ![]() для угловой координаты
для угловой координаты ![]() = 0, см. рис. 1.
= 0, см. рис. 1.
Для примера рассмотрим график, построенный для полуугла контакта ![]() = 2°, см. рис. 2. Экстремум этого графика соответствует безразмерному радиусу
= 2°, см. рис. 2. Экстремум этого графика соответствует безразмерному радиусу ![]() . Отсюда, зная
. Отсюда, зная ![]() , можно определить радиус
, можно определить радиус ![]() .
.
С увеличением полуугла контакта ![]() значение безразмерному радиусу
значение безразмерному радиусу ![]() , который соответствует экстремуму рассматриваемого графика, сначала уменьшается, а затем возрастает, см. рис. 2. Чтобы лучше понять это изменение на рис. 2 для сравнения приведен аналогичный график для случая, когда отверстие охватывающей детали нагружено равномерным давлением
, который соответствует экстремуму рассматриваемого графика, сначала уменьшается, а затем возрастает, см. рис. 2. Чтобы лучше понять это изменение на рис. 2 для сравнения приведен аналогичный график для случая, когда отверстие охватывающей детали нагружено равномерным давлением ![]() .
.

Рис. 2. Графики изменения безразмерных эквивалентных напряжений ![]() от безразмерного радиуса
от безразмерного радиуса ![]() для различных полууглов контакта
для различных полууглов контакта ![]()
С увеличением полуугла контакта j0 значение безразмерному радиусу ![]() , который соответствует экстремуму рассматриваемого графика, сначала уменьшается, а затем возрастает, см. рис. 2. Чтобы лучше понять это изменение на рис. 2 для сравнения приведен аналогичный график для случая, когда отверстие охватывающей детали нагружено равномерным давлением
, который соответствует экстремуму рассматриваемого графика, сначала уменьшается, а затем возрастает, см. рис. 2. Чтобы лучше понять это изменение на рис. 2 для сравнения приведен аналогичный график для случая, когда отверстие охватывающей детали нагружено равномерным давлением ![]() .
.
Графики, изображенные на рис. 2, неудобны для применения, поэтому они были перестроены. На рис. 3 даны графики зависимости наибольшего значения эквивалентных напряжениий ![]() и радиуса R его залегания от полуугла контакта
и радиуса R его залегания от полуугла контакта ![]() . Причем для удобства практического применения эти графики совмещены, а для общности даны в безразмерном виде.
. Причем для удобства практического применения эти графики совмещены, а для общности даны в безразмерном виде.
Для сравнения на рис. 3 пунктиром показаны аналогичные зависимости в контактной задаче Герца, применимой для малых полууглов контакта [8], когда кривизну отверстия в охватывающей детали не учитывают и площадку контакта считают плоской, линейчатой. Хорошая сходимость с общепризнанной задачей Герца, в зоне в которой она применима, подтверждает правильность выполненных теоретических исследований.

Рис. 3. Графики зависимости наибольшего эквивалентного напряжения ![]() и
и
радиуса R его залегания от полуугла контакта ![]()
2.5. Исследование деформированного состояния охватывающей детали (определение перемещений точек охватывающей детали).
На рис. 1 показана точка «А» с произвольными координатами ![]() и
и ![]() , когда охватывающая деталь 2 ненагружена. После приложения контактного давления
, когда охватывающая деталь 2 ненагружена. После приложения контактного давления ![]() точка «А» сместится в точка «А΄». При этом u – это ее радиальное перемещение, а v – окружное перемещение. Цель данного подраздела исследований – определение указанных перемещений.
точка «А» сместится в точка «А΄». При этом u – это ее радиальное перемещение, а v – окружное перемещение. Цель данного подраздела исследований – определение указанных перемещений.
Для данного исследования исходными являются выражения (6) – (9) для компонентов напряжений. Компоненты напряжений связаны следующими зависимостями Гука с радиальными ![]() , окружными
, окружными ![]() и угловыми
и угловыми ![]() деформациями:
деформациями:
![]() ; (10)
; (10)
![]() ; (11)
; (11)
![]() . (12)
. (12)
Подставим в уравнения (10) – (12) значения компонентов напряжений, см зависимости (6) – (9), и получим выражения для деформаций.
Зависимости Коши связывают полученные деформации с радиальными u и окружными v перемещениями:
![]() ; (13)
; (13)
![]() ; (14)
; (14)
![]() (15)
(15)
Подставим в уравнения (13) – (15) полученные выражения для деформаций. Затем проинтегрируем полученные зависимости и, сделав целый ряд преобразований, получим формулы для определения искомых перемещений
![]()
 , (16)
, (16)
Где
![]() (17)
(17)
 , (18)
, (18)
Где
![]() ; (19)
; (19)
![]() и
и ![]() – неизвестные функции.
– неизвестные функции.
После ряда преобразований получим следующее дифференциальное уравнение, в которое входят неизвестные функции ![]() и
и ![]()
![]() . (20)
. (20)
Решениями этого уравнения будут [6, 9]
![]() ; (21)
; (21)
![]() . (22)
. (22)
Произвольные постоянные ![]() ,
, ![]() и
и ![]() определяются из уравнений (16) и (18), используя свойство двойной симметрии задачи. В итоге получили
определяются из уравнений (16) и (18), используя свойство двойной симметрии задачи. В итоге получили ![]() и окончательные выражения для искомых перемещений
и окончательные выражения для искомых перемещений
![]()
 ; (23)
; (23)
 , (24)
, (24)
где ![]() и
и ![]() определяются по формулам (17) и (19), а коэффициенты ряда Фурье – из выражения (1).
определяются по формулам (17) и (19), а коэффициенты ряда Фурье – из выражения (1).
Построить удобные для практического применения графики по определению перемещений точек охватывающей детали не удалось, так как каждое из перемещений зависит от координат ![]() и
и ![]() , а также – от полуугла контакта
, а также – от полуугла контакта ![]() .
.
Для расчета перемещений в конкретной задаче необходимо разработать программу для ЭВМ, исходными данными для которой будут: радиусы деталей соединения ![]() и
и ![]() , протяженность контакта деталей вдоль оси L, модули упругости Е1 и Е2 и коэффициенты Пуассона
, протяженность контакта деталей вдоль оси L, модули упругости Е1 и Е2 и коэффициенты Пуассона ![]() и
и ![]() соединяемых деталей, суммарная силы F (погонная нагрузка q = F/L).
соединяемых деталей, суммарная силы F (погонная нагрузка q = F/L).
Далее, см. работу [1], по графикам определяются полуугол контакта ![]() и максимальное контактное давление рMAX, которые будут дополнительными исходными данными для расчета перемещений.
и максимальное контактное давление рMAX, которые будут дополнительными исходными данными для расчета перемещений.
Задаемся числом членов m ряда Фурье. Если ![]() , то рекомендуется m = 1500. В противном случае рекомендуется m = 1000. Рекомендуемые значения m с гарантией обеспечат точность расчетов, которая принята в п. 2.3 данной статьи.
, то рекомендуется m = 1500. В противном случае рекомендуется m = 1000. Рекомендуемые значения m с гарантией обеспечат точность расчетов, которая принята в п. 2.3 данной статьи.
Программируем вычисление радиального u и окружного v перемещений, см. формулы (23) и (24). При этом ![]() и
и ![]() определяются по формулам (17) и (19), а коэффициенты ряда Фурье, используя зависимость (1), соответственно равны
определяются по формулам (17) и (19), а коэффициенты ряда Фурье, используя зависимость (1), соответственно равны ![]() ;
; ![]() .
.
ВЫВОДЫ ПО РАБОТЕ
1. Работа посвящена исследованию напряженно-деформированного состояния безграничной в радиальном направлении охватывающей детали соединения цилиндрических деталей с малым зазором под действием контактного давления. Методика определения контактного давления изложена в предыдущей работе.
2. Исследование проводилось методами задачи плоской деформации теории упругости с известными допущениями.
3. В результате проведенного исследования получены зависимости по определению напряжений, деформаций и перемещений в точках охватывающей детали.
4. В результате анализа установлено, что для полуугла контакта ![]() точка, в которой действует наибольшие эквивалентные напряжения, располагается в глубине детали под максимальным контактным давлением на некотором радиусе R. Величина радиуса R зависит от
точка, в которой действует наибольшие эквивалентные напряжения, располагается в глубине детали под максимальным контактным давлением на некотором радиусе R. Величина радиуса R зависит от ![]() . Для полуугла контакта
. Для полуугла контакта ![]() указанная точка располагается на поверхности отверстия охватывающей детали.
указанная точка располагается на поверхности отверстия охватывающей детали.
5. Для инженерной методики расчета разработаны графики, позволяющие по значениям полуугла контакта, максимального контактного давления и радиуса отверстия в охватывающей детали определять максимальные эквивалентные напряжения в указанной детали и положение точки, в которой они возникают.
СПИСОК ЛИТЕРАТУРЫ
1. Блинов Д.С., Алешин В.Ф. Определение эпюры контактного давления для соединения деталей по цилиндрическим поверхностям с малым зазором (случай, когда охватывающая деталь безгранична в радиальном направлении). Электронный журнал «Наука и образование: электронное научно-техническое издание» МГТУ им.Баумана, # 05, май 2011.
2. Демидов С.П. Теория упругости. – М.: Высшая школа, 1979. – 432 с.
3. Тимошенко С.П., Гудьер Дж. Теория упругости. – М.: Наука, 1979. – 560 с.
4. Мышкис А. Д. Лекции по высшей математике. – М.: Наука, 1973. – 640 с.
5. Янке Е., Эмде Ф., Леш Ф. Специальные функции. – М.: Наука, 1964. – 344 с.
6. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. – М.: Наука, 1970. – 720 с.
7. Ланцош К. Практические методы прикладного анализа. – М.: Физматгиз, 1961. – 524 с.
8. Прочность, устойчивость, колебания: Справочник в 3-х томах. / Под ред. И.А.Биргера, Я.Г.Пановко . – М.: Машиностроение, т. 2, 1968. – 463 с.
9. Камке Э. Справочник по обыкновенным дифференциальным уравнениям. – М.: Наука, 1976. – 576 с.
Публикации с ключевыми словами: напряжения, перемещения, соединение деталей, радиальный зазор, полуугол контакта, эпюра контактного давления
Публикации со словами: напряжения, перемещения, соединение деталей, радиальный зазор, полуугол контакта, эпюра контактного давления
Смотри также:
- 77-30569/264652 Разработка методики расчета соединений деталей по цилиндрическим поверхностям с малым зазором для случая, когда охватывающая деталь тонкостенная
- 77-30569/315087 Погрешность формы тонкостенной заготовки при ее закреплении кулачками приспособления с учетом размеров площадки контакта сопрягаемых деталей.
- Инженерная методика расчета соединения деталей по цилиндрическим поверхностям с малым зазором (случай, когда охватывающая деталь безгранична в радиальном направлении). Примеры.
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



