научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 04, апрель 2011
УДК 621.833.1
РГТУ МАТИ
Метод определения качественных показателей зубчатых колес в зависимости от коэффициентов смещения по блокирующему контуру получил широкое распространение и развитие как для метода проектирования в обобщающих параметрах [2, 4], так и для традиционного метода проектирования [3, 5].
Проектирование зубчатых колес по заданной толщине зуба на вершине [1] позволяет сочетать преимущества геометрии проектирования в обобщающих параметрах с наглядностью традиционного метода проектирования.
Построение блокирующего контура по заданной толщине зуба на вершине позволит обеспечить наиболее высокую плавность работы и прочность зубчатой передачи при минимальном варьировании геометрических параметров,
Для построения блокирующего контура, по заданной толщине зуба на вершине требуется определить ряд параметров исходного контура по заданной толщине зуба на вершине.
К определяемым параметрам реечного инструмента относятся: коэффициент высоты головки ha* и коэффициент высоты ножки hf*.
В качестве исходных данных для расчета геометрии колеса используется модуль m, число зубьев колеса Z, угол исходного контура α, коэффициент радиального зазора c*, коэффициент смещения x.
На первом этапе коэффициент высоты головки принимается ha*=1.
Коэффициент высоты головки определяется величиной эвольвентного угла αa на вершине зуба. Этот угол должен быть определен по заданной толщине зуба на вершине.
Минимальная толщина зуба на вершине зависит от метода термообработки, вероятности сколов вершины, марки материала и т.д. Например, зубчатые колеса с модулем, равным 3 мм, редуктора винта двигателя ТВ7-117 имеют толщину зубьев на вершине равную 0.7 - 0.75 мм.
В работе [5] угол αa профиля на окружности вершин предлагается определять с помощью нанограмм по известным значениям угла профиля на окружности заострения - υ и относительной толщине зубцов на окружности вершин ma. Однако, данный подход не позволяет получить достаточную точность для расчетов.
В настоящей работе расчет эвольвентного угла αa предлагается выполнить с помощью минимизации целевой функции f = |Sα – Sζ|, где Sα - толщина зуба на вершине зубчатого колеса, которая может быть задана в долях модуля или как абсолютная величина (в миллиметрах), Sζ - толщина зуба в сечении, заданном варьируемым эвольвентным углом ζ методом золотого сечения, на интервале изменения эвольвентного угла 0<ζ< S/(2·d)+invα, где S - окружная толщина зуба на делительной окружности, d - делительный диаметр.
В результате минимизации целевой функции методом золотого сечения определяется величина эвольвентного угла ζискомый. Этот угол определит сечение, в котором толщина зуба Sζ с заданной точностью будет равна Sa. Этот угол соответствует углу профиля на окружности вершин.
αa = ζискомый
Таким образом, формулы определения коэффициента высоты головки зуба выглядят следующим образом:
ha*=((ra – r)/T – (T·x·m–TΣ ·ΔY·m))/m, где (1)
ra - радиус на окружности вершин,
r - радиус делительной окружности,
ΔY - уравнительное смещение,
TΣ = T1·T2 - тип зацепления, где:
Где T1,2 - параметр, определяющий тип зубьев шестерни и колеса в передаче и принимает значения: T=1, если зубья внешние; T=-1 если зубья внутренние.
Коэффициент высоты ножки зуба определяется по коэффициенту высоты головки сопряженного колеса.
hf*1= c0*1+ ha*2, (2)
hf*2= c0*2+ ha*1. (3)
Данный подход позволяет построить новую область существования зубчатого зацепления, в каждой точке которой меняется коэффициент высоты головки зуба, сохраняя толщину зуба на вершине постоянной (рис. 1).

В любой точке закрашенного контура толщина зуба на вершине будет равна заданной величине Sa. При этом коэффициенты высоты головки исходного контура вычисляются по формулам (1-3).
При изменении метода проектирования меняется область существования зубчатой передачи. В результате этого точка, находящаяся внутри области существования, при проектировании по ОСТ 1 00258-77 может находиться вне области существования построенной для метода проектирования по заданной толщине зуба на вершине.
Получение блокирующего контура для метода проектирования по заданной толщине зуба на вершине позволяет провести сравнение методов проектирования.
Рассмотрим результаты данного исследования на примере авиационной прямозубой зубчатой передачи со следующими геометрическими параметрами:
Число зубьев Z1=27, Z2 = 48, угол исходного контура α = 25°, коэффициент радиального зазора c0*1 = c0*1 = 0.20328, модуль m = 3, ширина зубчатого венца b = 40,5 мм. Режим нагружения: частота вращения 7500 об/мин, передаваемая мощность 400 кВт.
Результат компьютерного моделирования напряжений и вибраций в зубчатой передаче, колеса которой рассчитаны по ОСТ 1 00258-77, показан на рис. 2. Коэффициент высоты головки при этом методе расчета был принят ha*=1.
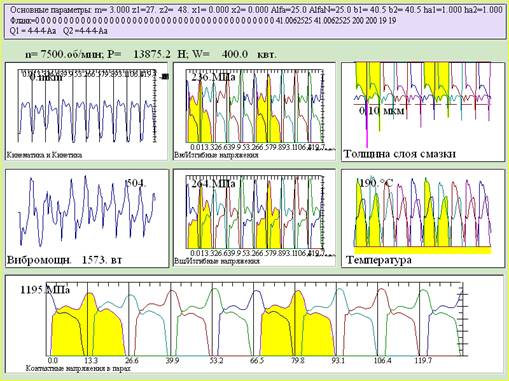
Рис. 2. Результат прочностного расчета при проектировании по ОСТ 1 00258-77.
Следующим шагом сравнения была фиксация толщины зуба на вершине Sa = 0.8 (рис. 3). Коэффициент высоты головки был рассчитан по формулам (1-3).

Рис. 3. Значения геометрических параметров при проектировании по заданной толщине зуба на вершине.
Результат компьютерного моделирования напряжений и вибраций при проектировании геометрии по заданной толщине зуба на вершине показан на рис. 4.
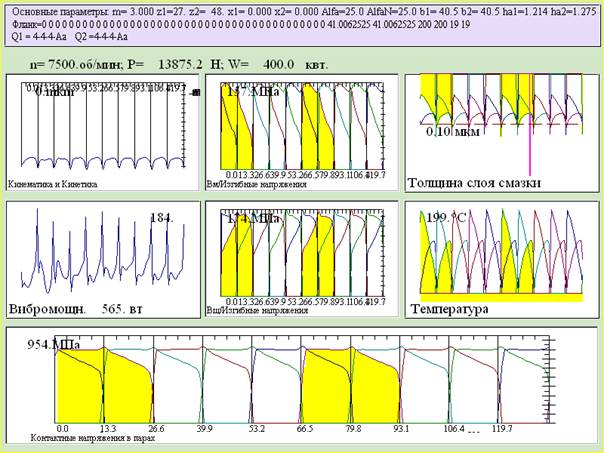
Рис. 4. Результат прочностного расчета при проектировании по заданной толщине зуба на вершине
Как видно из рис. 4 и рис. 2 метод проектирования по заданной толщине зуба на вершине обеспечил снижение контактных напряжений на 20 %, изгибных напряжений на 30%, величины вибрации на 64 %.
Выводы
Блокировочные контура, используемые при проектировании авиационных зубчатых передач должны быть связаны с современными методиками проектирования. Данная задача была решена методами нелинейного программирования, что дает возможность максимально упростить процесс проектирования авиационных зубчатых передач.
Использование метода проектирования по заданной толщине зуба на вершине позволяет существенно упростить процесс проектирования и достигнуть увеличения прочностных показателей зубчатых передач.
Список литературы
[1] Дорофеев Д.В., Шевченко И.В. Метод синтеза эвольвентного зубчатого зацепления для передач авиационной техники//Авиационная промышленность, 2010, ╧1, стр. 39-42
[2] ОСТ 1 00480-83 «Передачи зубчатые цилиндрические эвольвентные внешнего зацепления. Расчет геометрии в обобщающих параметрах»
[3] ОСТ 1 00258-77 «Передачи зубчатые цилиндрические эвольвентные прямозубые внешнего зацепления. Расчет геометрических параметров»
[4] Болотовская Т. П., Болотковский И. А., Смирнов В. Э. Справочник по корригированию зубчатых колес, Машгиз, 1962
[5] Вулгаков Э. Б. Теория эвольвентных зубчатых передач. - М. Машиностроение, 1995, 320 с.
[6] Химмельблау Д. Прикладное нелинейное программирование. М.: Мир, 1975, 534 с.
Публикации с ключевыми словами: проектирование, зубчатые передачи, оптимизация
Публикации со словами: проектирование, зубчатые передачи, оптимизация
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



