научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 03, март 2011
УДК: 621.396.662
МГТУ им. Н.Э.Баумана.
Введение
Помехоустойчивость систем синхронизации до недавнего времени исследовалась лишь при шумовом воздействии [1-8]. При этом на основе теории марковских случайных процессов – уравнений Фоккера-Планка-Колмогорова (ФПК) и уравнений Понтрягина найдены статистические характеристики фазовой автоподстройки частоты (ФАП) такие, как плотность распределения вероятности (ПРВ) сигнала рассогласования (фазовой ошибки), среднее значение частотного рассогласования, среднее значение частоты срывов синхронизации (перескоков фазы), а также вероятность срывов синхронизации. Следует отметить, что ПРВ сигнала ошибки была получена в общем случае наличия частотного рассогласования как в интегральном виде [1,2], так и в форме быстросходящегося ряда [3,4,8]. Статистическая динамика ФАП исследована при различных характеристиках фазового дискриминатора [4].
С развитием радиотехники, систем связи и космической радионавигации возникла необходимость исследовать системы синхронизации не только при шумовых воздействиях, но и при комбинированных воздействиях, состоящих из аддитивной смеси сигнала, гармонической помехи и шума.
Работы, посвящённые анализу статистических характеристик системы синхронизации при комбинированных воздействиях, исчисляются до настоящего времени единицами [9-13].
В указанных работах рассматриваются, как правило, воздействия на ФАП, наряду с шумом гармонической помехи, причём, статистические характеристики, как правило, находятся в наихудшем случае отсутствия частотной расстройки между сигналом и помехой [9-11], и сами статистические характеристики, получаемые различными авторами, не сравниваются между собой.
В настоящей работе на основе аппарата марковских случайных процессов (уравнения ФПК) путём использования различных приближений получены статистические характеристики фазовой автоподстройки частоты. В первую очередь это ПРВ сигнала рассогласования, частота срывов синхронизации, а также средняя разность между колебаниями управляемого генератора и сигнала при комбинированном воздействии на вход ФАП в виде аддитивной смеси сигнала, суммы нескольких гармонических помех и гауссовского шума.
1. Модель системы ФАП при воздействии на вход системы аддитивной смеси сигнала, гармонической помехи и шума
Допустим, что на вход ФАП поступает аддитивная смесь полезного сигнала (эталонного колебания) ![]() , гармонической помехи
, гармонической помехи ![]() и полосового (белого) гауссовского шума
и полосового (белого) гауссовского шума ![]() (рис. 1):
(рис. 1):
![]() .
.

Рис. 1. Структурная схема ФАП
Эталонное колебание
![]() (1)
(1)
где А – среднеквадратическое значение напряжения полезного сигнала;
![]() - частота сигнала, совпадающая с начальной частотой управляемого генератора (УГ);
- частота сигнала, совпадающая с начальной частотой управляемого генератора (УГ); ![]() и
и ![]() - начальные расстройки по частоте и фазе между эталонным колебанием и сигналом на выходе УГ.
- начальные расстройки по частоте и фазе между эталонным колебанием и сигналом на выходе УГ.
Гармоническую помеху примем в виде
 (2)
(2)
где N – число спектральных составляющих, попадающих в полосу пропускания линейного тракта, предшествующего ФАП; ![]() - среднеквадратическое значение напряжения i-ой спектральной составляющей;
- среднеквадратическое значение напряжения i-ой спектральной составляющей; ![]() и
и ![]() начальные расстройки по частоте и фазе i-ой составляющей относительно частоты и фазы на входе УГ.
начальные расстройки по частоте и фазе i-ой составляющей относительно частоты и фазы на входе УГ.
Полосовой гауссовский шум имеет вид
![]() (3)
(3)
где ![]() и
и ![]() - независимые квадратурные гауссовские случайные процессы. По предположению, двусторонняя спектральная плотность шума равна
- независимые квадратурные гауссовские случайные процессы. По предположению, двусторонняя спектральная плотность шума равна ![]() (Вт/Гц).
(Вт/Гц).
Фазовый детектор перемножает поступающие на его вход колебания. Напряжение на выходе фазового детектора имеет вид
![]()
Здесь ![]() - коэффициент передачи фазового детектора;
- коэффициент передачи фазового детектора;
![]() - напряжение на выходе УГ, (4)
- напряжение на выходе УГ, (4)
где ![]() - среднеквадратическое значение напряжения на выходе генератора;
- среднеквадратическое значение напряжения на выходе генератора; ![]() - медленно меняющаяся фаза колебания УГ в режиме подстройки.
- медленно меняющаяся фаза колебания УГ в режиме подстройки.
Пренебрегая вторыми гармониками, которые формируются после перемножения колебаний ![]() и
и ![]() , получим низкочастотную составляющую колебания на выходе фазового детектора.
, получим низкочастотную составляющую колебания на выходе фазового детектора.
![]()
где

Фильтр низких частот (ФНЧ) описывается операторным коэффициентом передачи (передаточной функцией) ![]() ,
, ![]() .
.
Сигнал на выходе фильтра описывается в символическом виде
![]()
Управляемый генератор (УГ) преобразует управляющее воздействие ![]() в изменение фазы генерируемых колебаний
в изменение фазы генерируемых колебаний ![]() , так что
, так что
![]() ,
,
где ![]() [рад/с*В] – коэффициент передачи УГ (крутизна модуляционной характеристики УГ).
[рад/с*В] – коэффициент передачи УГ (крутизна модуляционной характеристики УГ).
Таким образом,
![]() ,
,
где ![]() - коэффициент усиления разомкнутой цепи регулирования.
- коэффициент усиления разомкнутой цепи регулирования.
Осуществим замену переменной
![]() .
.
Переменная ![]() называется сигналом рассогласования или сигналом ошибки – это разность фаз эталонного колебания УГ на выходе управляемого генератора.
называется сигналом рассогласования или сигналом ошибки – это разность фаз эталонного колебания УГ на выходе управляемого генератора.
Обозначим низкочастотный шум, или шум, пересчитанный на выход фазового детектора, в виде
![]() .
.
Низкочастотный шум ![]() в пределах полосы пропускания ФАП является гауссовским шумом, который моделируется гауссовским белым шумом (ГБШ) с двусторонней спектральной плотностью
в пределах полосы пропускания ФАП является гауссовским шумом, который моделируется гауссовским белым шумом (ГБШ) с двусторонней спектральной плотностью ![]() (Вт/Гц).
(Вт/Гц).
В результате преобразований получим стохастическое дифференциальное уравнение (ДУ) в символической форме
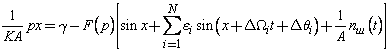 , (5)
, (5)
где ![]() - относительная расстройка по частоте эталонного колебания и сигнала с выхода УГ;
- относительная расстройка по частоте эталонного колебания и сигнала с выхода УГ; ![]() ;
; ![]() ;
;![]() ;
; ![]() .
.
Структурная схема ФАП, соответствующая ДУ (5), изображена на рис. 2.
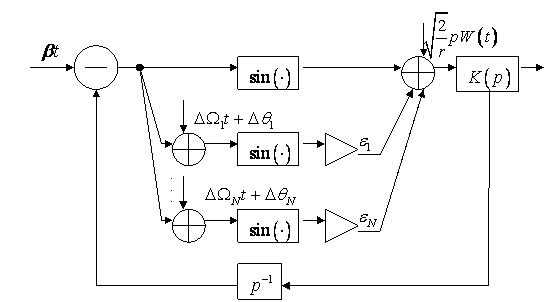
Рис. 2. Структурная схема ФАП
Если вместо параметра А ввести величину ![]() , то стохастическое ДУ в новых обозначениях при наличии одной гармоники в помехе принимает вид
, то стохастическое ДУ в новых обозначениях при наличии одной гармоники в помехе принимает вид
![]() , (6)
, (6)
где ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() – отношение помеха/сигнал (ОПС).
– отношение помеха/сигнал (ОПС).
2. Стохастическая модель системы
Рассмотрим воздействие одной гармоники совместно с шумом, когда частота помехи находится за полосой синхронизации.
Запишем ДУ (6) в виде
 (7)
(7)
где t0 – момент начала наблюдений;
![]()
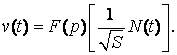
Если v(t)=0, то ДУ (7) соответствует детерминированному случаю, когда решение ДУ (7) можно исследовать методом гармонического баланса [12], положив
![]() (8)
(8)
где x0 и x1 – некоторые константы, причем амплитуда x1 в первом приближении не зависит от x0 и имеет вид [12]
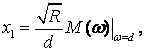 (9)
(9)
где ![]()
Случайное воздействие v(t) в (7) формируется из ГБШ посредством низкочастотного фильтра и вследствие этого является низкочастотным. На интервале корреляции случайного процесса v(t) при ![]() укладывается значительное число периодов гармонической составляющей фазового рассогласования, поэтому можно считать, что наличие воздействия v(t) приводит лишь к медленному изменению фазовой ошибки, а параметры гармонической составляющей практически не изменяются.
укладывается значительное число периодов гармонической составляющей фазового рассогласования, поэтому можно считать, что наличие воздействия v(t) приводит лишь к медленному изменению фазовой ошибки, а параметры гармонической составляющей практически не изменяются.
Таким образом, при v(t)![]() можно принять решение [8] в виде
можно принять решение [8] в виде
![]() (10)
(10)
где ![]() и
и ![]() - константы, рассчитываемые по (9), а также по формуле
- константы, рассчитываемые по (9), а также по формуле
![]() (11)
(11)
Функция z(t) изменяется медленно по сравнению с ![]() .
.
Рассмотрим один период гармонической составляющей фазового рассогласования x(t), когда можно приближенно положить z(t)=const. Тогда воздействие y(t) оказывается периодическим с периодом ![]() и его можно разложить в ряд Фурье на интервале [t, t+T]
и его можно разложить в ряд Фурье на интервале [t, t+T]
 .
.
На изменение низкочастотной составляющей фазовой ошибки z(t) влияет главным образом слагаемое вида ![]() поэтому на основе (10) можно записать
поэтому на основе (10) можно записать
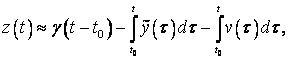 (12)
(12)
причем после усреднения находим
![]()
где ![]() и
и ![]() - функции Бесселя порядков 0 и 1 соответственно.
- функции Бесселя порядков 0 и 1 соответственно.
Уравнение (1.12) эквивалентно стохастическому ДУ
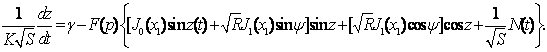 (13)
(13)
Данное уравнение описывает изменение во времени усредненной во времени фазовой ошибки (или детерминированной составляющей фазовой ошибки) при одновременном воздействии на систему синхронизации широкополосного шума и узкополосной помехи, частота которой лежит за пределами полосы синхронизации.
Для расчета параметров гармонической составляющей фазовой ошибки (8) используются соотношения (9) и (11). С учётом (11) стохастическое ДУ (13) принимает вид
 (14)
(14)
где ![]()
![]() - стандартный винеровский случайный процесс;
- стандартный винеровский случайный процесс;
 - ОСШ на выходе линеаризованной ФАП первого порядка;
- ОСШ на выходе линеаризованной ФАП первого порядка;
 - шумовая полоса такой ФАП;
- шумовая полоса такой ФАП; ![]() .
.
На рис. 3 изображены зависимости от времени решения x(t) и z(t) в системе первого порядка ![]() , K=S=1; R=1, d=4;
, K=S=1; R=1, d=4; ![]() =0,5; ОСШ r=30 дБ.
=0,5; ОСШ r=30 дБ.

Рис. 3. Траектория фазовой ошибки для первого порядка ФАП
Стохастическое ДУ (13) и (14) имеют независящие от времени коэффициенты и поэтому к ним применима теория марковских случайных процессов и возможен переход от ДУ (13), (14) к уравнению ФПК.
3. Анализ стохастической системы ФАП первого порядка
Стохастическое ДУ в данном случае находится по (14) при ![]()
Тогда по (14) получим

Этому ДУ соответствует уравнение ФПК
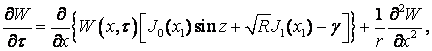 (15)
(15)
где ![]() .
.
Предположим, что имеет место стационарный режим работы ФАП, тогда ![]() и по (15) приходим к ДУ
и по (15) приходим к ДУ
![]() (16)
(16)
где ![]()
Решением ДУ (16) является [4, формула (1.38)]
 (17)
(17)
где 
![]()
![]()
Отсюда находим


причём

При ![]() по (16) следует формула Тихонова [1]. При R=0 и
по (16) следует формула Тихонова [1]. При R=0 и ![]() получаем видоизмененные стандартные формулы для расчёта ФАП с синусоидальной нелинейностью без учёта гармонической помехи [4]. Наконец, при
получаем видоизмененные стандартные формулы для расчёта ФАП с синусоидальной нелинейностью без учёта гармонической помехи [4]. Наконец, при ![]() и
и ![]() можно установить формальную аналогию между (17) и соотношениями для расчёта обычной ФАП с синусоидальной нелинейностью, если ввести приведённую расстройку по частоте
можно установить формальную аналогию между (17) и соотношениями для расчёта обычной ФАП с синусоидальной нелинейностью, если ввести приведённую расстройку по частоте ![]() и приведённое ОСШ
и приведённое ОСШ ![]()
Справедливо разложение ПРВ W(x) в ряд Фурье [12].
 .
.
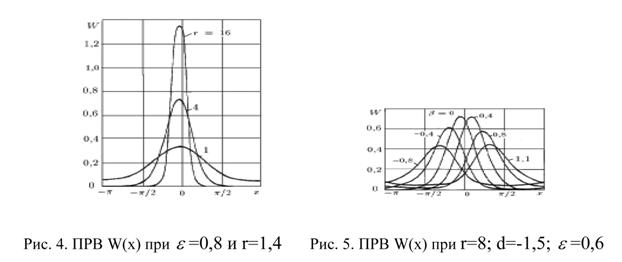
На рис. 4 и рис. 5 изображены ПРВ W(x) при различных значениях r и ![]() . На рис. 4
. На рис. 4 ![]() =0,8 и r=1,4; 16
=0,8 и r=1,4; 16 ![]() на рис. 5 r=8; d=-1,5;
на рис. 5 r=8; d=-1,5; ![]() =0,6;
=0,6; ![]()
Среднее время до срыва слежения находится решением уравнения Понтрягина
 (18)
(18)
где ![]() – нормированное значение среднего времени Тс до срыва синхронизации.
– нормированное значение среднего времени Тс до срыва синхронизации.
После преобразования решения этого уравнения получим среднее время до срыва слежения в виде
 (19)
(19)
На рис. 6, 7 даны графики зависимостей ![]() при
при ![]() и различных значениях
и различных значениях ![]() (на рис. 6 при d=1,5; на рис. 7 при d=-1,5).
(на рис. 6 при d=1,5; на рис. 7 при d=-1,5).

По рис. 6, 7 заметны различия в свойствах системы при d>0 и d<0, а именно: при d>0 увеличение ![]() приводит к росту (при любых r) среднего времени до срыва слежения; при d<0 имеется обратная тенденция.
приводит к росту (при любых r) среднего времени до срыва слежения; при d<0 имеется обратная тенденция.
Это явление подтверждается результатами анализа детерминированной системы [12].
Наличие мощной помехи за пределами полосы синхронизации улучшает слежение, если сигнал и помеха имеют одинаковые по знаку отстройки от частоты собственных колебаний управляемого генератора и ухудшает слежение, если знаки расстроек противоположные.
На рис. 8, 9 иллюстрированы зависимости ![]() при различных значениях
при различных значениях ![]() , если имеет место положительная (d=1,5, рис. 8) и отрицательная (d=-1,5, рис. 9) отстройка помехи от частоты собственных колебаний управляемого генератора.
, если имеет место положительная (d=1,5, рис. 8) и отрицательная (d=-1,5, рис. 9) отстройка помехи от частоты собственных колебаний управляемого генератора.

Наконец найдем среднее значение частотного рассогласования. Можно показать, что справедливо соотношение [12]
 (20)
(20)
где ![]()
![]() - среднее значение частотного рассогласования между частотой сигнала и частотой управляемого генератора.
- среднее значение частотного рассогласования между частотой сигнала и частотой управляемого генератора.
На рис. 10-13 даны графики зависимостей ![]() при
при ![]() и соответственно при d=1,5 и d=-1,5.
и соответственно при d=1,5 и d=-1,5.


4. Стохастические характеристики ФАП при воздействии прицельной помехи
В этом случае расстройка ![]() и уравнение ФПК для ФАП первого порядка имеет вид [12]
и уравнение ФПК для ФАП первого порядка имеет вид [12]
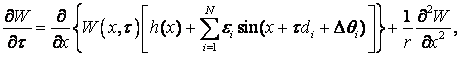 (1.21)
(1.21)
где ![]()
Пусть N=1; ![]() и имеет место стационарный режим работы ФАП. Тогда
и имеет место стационарный режим работы ФАП. Тогда ![]() и ДУ ФПК принимает вид
и ДУ ФПК принимает вид
 (22)
(22)
где ![]() .
.
Введем обозначение
![]() (23)
(23)
Решение уравнения (22) записывается в виде [4]
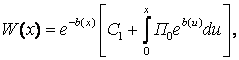 (24)
(24)
где 

![]()
![]()
 , причем условие
, причем условие ![]() означает стационарность потока вероятности
означает стационарность потока вероятности ![]() .
.
Функция W(x) удовлетворяет условиям
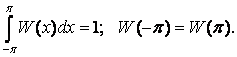 (25)
(25)
Тогда [4,14]
 (26)
(26)
где ![]()

где ![]()
Для практических вычислений можно использовать три альтернативных подхода: во-первых, таблицы; во-вторых, интегральное представление через модифицированную функцию Бесселя нулевого порядка [14]

в-третьих, разложение в ряд [3,4]
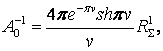 (27)
(27)
где

В частном случае при ![]() (т.е. при отсутствии расстройки по частоте между эталонным колебанием и сигналом на выходе генератора) справедливо равенство П0=0, поэтому
(т.е. при отсутствии расстройки по частоте между эталонным колебанием и сигналом на выходе генератора) справедливо равенство П0=0, поэтому
![]() (28)
(28)
где ![]()
Отсюда при ![]() (т.е. при отсутствии помехи) получаем формулу Тихонова
(т.е. при отсутствии помехи) получаем формулу Тихонова
![]()
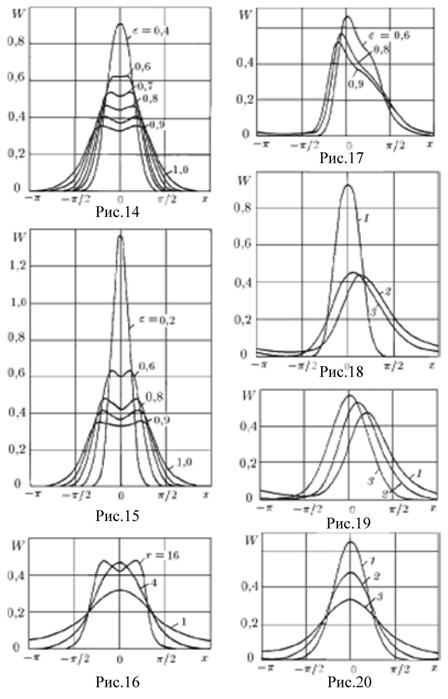
На рис. 14-17 приведены графики ПРВ W(x) при ![]() и разных значения параметров r и
и разных значения параметров r и ![]() : на рис. 14 r=12, на рис. 15 r=16, на рис. 16
: на рис. 14 r=12, на рис. 15 r=16, на рис. 16 ![]() =0,8, на рис. 17 r=16,
=0,8, на рис. 17 r=16, ![]() .
.
![]()
Плотность распределения вероятности W(x) была усреднена по ![]() в предположении, что
в предположении, что ![]() распределено равномерно в интервале
распределено равномерно в интервале ![]() . Поскольку точное значение
. Поскольку точное значение ![]() на практике, как правило, неизвестно, усреднение оправдано.
на практике, как правило, неизвестно, усреднение оправдано.
По рис. 14-16 замечаем бимодальность ПРВ W(x) при ![]() , близких к единице [9].
, близких к единице [9].
На рис. 18-20 приводятся графики ПРВ W(x) при следующих параметрах: на рис. 18: ![]()
![]() ;
;
на рис. 19: ![]() ;
;
на рис. 20: ![]() .
.
Ранее предполагалось, что в полосе пропускания ФАС присутствует только одна спектральная составляющая (N = 1). Это ограничение на самом деле не является существенным.
Пусть N > 1, но частота всех спектральных составляющих помехи практически одинакова и совпадает с частотой входного сигнала: ![]() . Тогда уравнение ФПК принимает вид
. Тогда уравнение ФПК принимает вид
 (29)
(29)
Используя свойства тригонометрических функций, получаем

где 
Таким образом, заменяя ![]() на
на ![]() и
и ![]() на
на ![]() , можно распространить полученные результаты на случай N > 1.
, можно распространить полученные результаты на случай N > 1.
Предположим, что ФАП безинерционна, т.е. K(p)=1; ![]() ; число спектральных составляющих помехи N=1; расстройка по частоте между гармонической помехой и эталонным колебанием отсутствует:
; число спектральных составляющих помехи N=1; расстройка по частоте между гармонической помехой и эталонным колебанием отсутствует: ![]() . Обозначим фазовую расстройку
. Обозначим фазовую расстройку ![]() и относительную интенсивность помехи
и относительную интенсивность помехи ![]() .
.
Уравнение Понтрягина запишем в виде [4]

где ![]() - нормированное среднее время; x имеет другой физический смысл, чем в уравнение ФПК: в данном случае это начальное значение фазовой ошибки в некоторый фиксированный момент времени t0.
- нормированное среднее время; x имеет другой физический смысл, чем в уравнение ФПК: в данном случае это начальное значение фазовой ошибки в некоторый фиксированный момент времени t0.
Общее решение уравнения Понтрягина имеет вид

где 
Функция ![]() должна удовлетворять граничным условиям
должна удовлетворять граничным условиям
![]()
следовательно
где 
После преобразований, аналогичных [4, гл.1], при ![]() находим
находим
![]()
Используя [4, формула (3.1)], получаем

Отсюда, при ![]() получаем известный результат [4, формула (3.2)]
получаем известный результат [4, формула (3.2)]
![]()
На рис. 21-23 даны графики зависимостей ![]() при различных значениях параметров
при различных значениях параметров ![]() и
и ![]() . На рис. 21
. На рис. 21 ![]() =0; на рис. 22
=0; на рис. 22 ![]() =0,4; на рис. 23
=0,4; на рис. 23 ![]() =0,6. Зависимости усреднены в предположении, что
=0,6. Зависимости усреднены в предположении, что ![]() распределено равномерно в интервале
распределено равномерно в интервале ![]() .
.
Пусть, как и ранее, K(p)=1; N=1; ![]() ;
; ![]() и
и ![]() . Вычислим среднее значение разности частот двух сигналов: эталонного, поступающего на вход ФАС в смеси с помехой, и опорного, вырабатываемого управляемым генератором в установившемся режиме.
. Вычислим среднее значение разности частот двух сигналов: эталонного, поступающего на вход ФАС в смеси с помехой, и опорного, вырабатываемого управляемым генератором в установившемся режиме.
С учётом приведённых условий после усреднения правой и левой частей ДУ (5) получаем
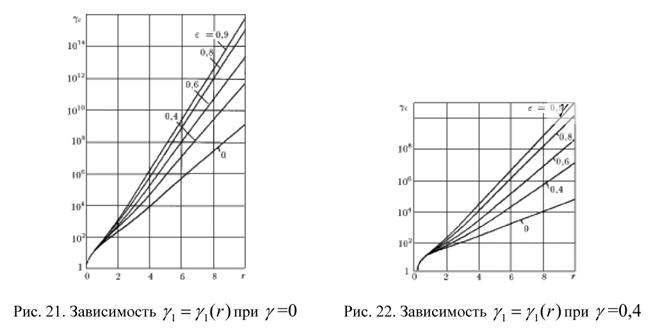

Рис. 23. Зависимость ![]() при
при ![]() =0,6
=0,6

где ![]() - среднее значение производной фазового рассогласования в системе.
- среднее значение производной фазового рассогласования в системе.
Интегрируя (23) в пределах ![]() , найдём
, найдём

так как в силу гармонических условий, накладываемых на ![]() ,
,
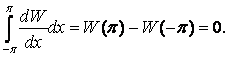
Таким образом,
![]()
Но, с другой стороны, по (26)

Следовательно,

Сравнивая это выражение для ![]() с уравнением ФПК, получаем
с уравнением ФПК, получаем
![]()
Тогда
![]() (30)
(30)
Используя (27), получим окончательный результат:
 (31)
(31)
При ![]() =0, (т.е. при отсутствии помехи) средняя разность частот эталонного и опорного сигналов в ФАС с синусоидальной нелинейностью имеет вид [4, формула 4.3]
=0, (т.е. при отсутствии помехи) средняя разность частот эталонного и опорного сигналов в ФАС с синусоидальной нелинейностью имеет вид [4, формула 4.3]
 (32)
(32)
Сравнивая (29) и (31) замечаем, что выполняется равенство
![]() (33)
(33)
На рис. 24-25 даны графики зависимостей ![]() при различных значениях параметров
при различных значениях параметров ![]() и
и ![]() : на рис. 24
: на рис. 24 ![]() =0,8; на рис. 25
=0,8; на рис. 25 ![]() =0,6.
=0,6.

Следует иметь ввиду, что величина ![]() при построении графиков была усреднена по
при построении графиков была усреднена по ![]() в предположении равномерного распределения этого параметра, поэтому формула (33), связывающая
в предположении равномерного распределения этого параметра, поэтому формула (33), связывающая ![]() с
с ![]() при фиксированном
при фиксированном ![]() для графических зависимостей
для графических зависимостей ![]() и
и ![]() не выполняется [9].
не выполняется [9].
5. Плотность распределения вероятностей сигнала рассогласования при наличии прицельной (коканальной) помехи (альтернативный подход) [10, 15]
Если принять воздействующий на ФАП сигнал в виде ![]() а помеху в общем случае в виде
а помеху в общем случае в виде ![]() где
где ![]() - это ОПС,
- это ОПС, ![]() - разность частот сигнала и помехи,
- разность частот сигнала и помехи, ![]() - разность фаз сигнала и помехи. Тогда по (5) придем к следующему стохастическому ДУ [10]
- разность фаз сигнала и помехи. Тогда по (5) придем к следующему стохастическому ДУ [10]
![]() (34)
(34)
где ![]() - ГБШ, имеющий двустороннюю спектральную плотность N0/2 (Вт/Гц).
- ГБШ, имеющий двустороннюю спектральную плотность N0/2 (Вт/Гц).
В случае прицельной помехи ![]() =0, а также полагая
=0, а также полагая ![]() получим стохастическое ДУ ФАП первого порядка
получим стохастическое ДУ ФАП первого порядка
![]() (35)
(35)
Это ДУ можно привести к виду [10]
![]() (36)
(36)
где ![]() (37)
(37)
 (38)
(38)
Следует отметить, что изменение во времени сигнала рассогласования Ф(t) в режиме слежения определяется двумя возмущающими факторами: n(t) и ![]() , причем
, причем ![]() является медленно меняющейся функцией по сравнения с широкополосным гауссовским шумом n(t). Вследствие этого новые переменные
является медленно меняющейся функцией по сравнения с широкополосным гауссовским шумом n(t). Вследствие этого новые переменные
а(t) и ![]() также будут медленно изменяться по сравнению с n(t) и в результате можно пренебречь производной
также будут медленно изменяться по сравнению с n(t) и в результате можно пренебречь производной ![]() по сравнению с
по сравнению с ![]() .
.
Для того, чтобы получить ПРВ W(Ф) по (36) необходимо заменить а(t) и ![]() на их мгновенные значения, так как а(t) и
на их мгновенные значения, так как а(t) и ![]() изменяются значительно медленнее по сравнению с Ф(t).
изменяются значительно медленнее по сравнению с Ф(t).
Используя стандартный переход от (36) к уравнению ФПК и решая это уравнение, получим условную ПРВ ![]() , а после интегрирования по всем значениям а и
, а после интегрирования по всем значениям а и ![]() получим совместную ПРВ
получим совместную ПРВ ![]() , в результате получим искомую ПРВ W(Ф).
, в результате получим искомую ПРВ W(Ф).
Совместная ПРВ ![]() при а и
при а и ![]() , определяемых по (37), (38),
, определяемых по (37), (38),
может быть найдена, если известна ПРВ СВ ![]() .
.
Используя [15], получим совместную ПРВ ![]() в виде
в виде
![]() (39)
(39)
где ![]() а и
а и ![]() находятся в диапазоне
находятся в диапазоне
![]() (40)
(40)
![]() (41)
(41)
и, кроме того, ![]() =0 в другой области, в (39)
=0 в другой области, в (39) ![]() - дельта – функция.
- дельта – функция.
Для удобства дальнейших преобразований целесообразно ПРВ (39) представить в виде
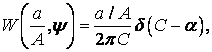 (42)
(42)
где ![]() где диапазон (40) преобразуем к виду
где диапазон (40) преобразуем к виду
![]()
На основе стохастического ДУ (36), переходя к уравнению ФПК и решая его, приходим к аналогу формулы Тихонова [4]
 (43)
(43)
где ![]() - модифицированная функция Бесселя нулевого порядка,
- модифицированная функция Бесселя нулевого порядка,
а параметр ![]() - это ОСШ, определяемое равенством
- это ОСШ, определяемое равенством
![]() (44)
(44)
Заменяя величину ![]() на произведение
на произведение ![]() , где
, где ![]() - ОСШ в отсутствии помехи, то по (43) получим
- ОСШ в отсутствии помехи, то по (43) получим
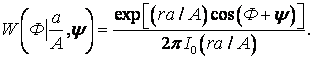 (45)
(45)
Используя (42) и (45) получим искомую ПРВ Ф(t) в виде
 (46)
(46)
Используя фильтрующее свойство дельта – функции, получим
 (47)
(47)
где  (48)
(48)
По (47) видно, что ПРВ Ф(t) является суммой двух интегралов: один при положительном знаке при функции ![]() , а другой при отрицательном знаке. По результатам расчета получены графики рис. 26, 27.
, а другой при отрицательном знаке. По результатам расчета получены графики рис. 26, 27.

![]()
![]()
Дисперсия фазовой ошибки находится по известной формуле (рис. 28)
 (49)
(49)

По результатам анализа ПРВ ![]() при наличии прицельной помехи (рис. 14-16, а также рис. 26, 27) можно сделать следующие выводы:
при наличии прицельной помехи (рис. 14-16, а также рис. 26, 27) можно сделать следующие выводы:
1. Из-за наличия помехи на частоте сигнала на графике ПРВ W(x) [или ![]() ] возникает двумодальность ПРВ, а следовательно и провалы в графике при x=0 (Ф=0).
] возникает двумодальность ПРВ, а следовательно и провалы в графике при x=0 (Ф=0).
2. При некоторых значениях ОСШ график ПРВ уплощается с уменьшением максимального значения при увеличении мощности помехи.
3. Наличие помехи увеличивает дисперсию сигнала рассогласования при любом значении ОСШ (см. рис. 28), причем характер зависимости ![]() монотонный несмотря на проявляющуюся бимодальность ПРВ при
монотонный несмотря на проявляющуюся бимодальность ПРВ при ![]() .
.
Далее, если сравнивать действие прицельной помехи и помехи с частотой, лежащей вне полосы синхронизации, то следует заметить, что дисперсия фазовой ошибки с ростом ![]() сигнала увеличивается, а затем уменьшается, но одновременно растет установившееся значение фазовой ошибки.
сигнала увеличивается, а затем уменьшается, но одновременно растет установившееся значение фазовой ошибки.
В случае прицельной помехи установившееся значение фазовой ошибки при ![]() независимо от величины ОПС
независимо от величины ОПС ![]() равна нулю.
равна нулю.
Сравнивая рис. 6 (помеха за полосой синхронизации) и рис. 22 (помеха внутри полосы синхронизации) замечаем важное различие между свойствами системы: помеха за пределами полосы синхронизации существенно ухудшает качество системы, снижая среднее время до срыва синхронизации на несколько порядков при одних и тех же значениях ОПС ![]() , ОСШ r и
, ОСШ r и ![]() .
.
Отмечается асимметрия свойств ФАП при наличии гармонической помехи за пределами полосы синхронизации, если расстройки по частоте полезного сигнала и помехи относительно частоты собственных колебаний управляемого генератора имеют одинаковый и разный знаки. В первом случае увеличение интенсивности помехи приводит к улучшению синхронизма, растет среднее время до срыва слежения и падает среднее значение частотного рассогласования; во-втором случае тенденция обратная.
Литература
1. Тихонов В.И. Влияние шумов на работу схемы фазовой автоподстройки частоты // Автоматика и телемеханика. 1959. ╧9. С. 1188-1196.
2. Тихонов В.И. Работа фазовой автоподстройки частоты при наличии шумов // Автоматика и телемеханика. 1960. ╧3. С.301-309.
3. Шахтарин Б.И. Анализ асимптотических значений статистических характеристик системы ФАПЧ // Радиотехника и электроника. 1986, ╧2. С. 246-258.
4. Шахтарин Б.И. Анализ систем синхронизации при наличии помех. - М.: ИПРЖР, 1996. 252 с.
5. Витерби А. Исследование динамики систем фазовой автоподстройки частоты в присутствии шумов с помощью уравнения Фоккера-Планка // ТИИЭР. М., 1963. Т. 51. ╧12. С. 1704-1722.
6. Витерби Э.Д. Принципы когерентной связи. М.: Сов. радио, 1970. 350 с.
7. Линдсей В. Системы синхронизации в связи и управлении: Пер. с англ. / Под ред. Ю.Н. Бакаева и М.В. Капранова. М.: Сов. Радио, 1978. 600 с.
8. Шахтарин Б.И. Спектральный анализ фазовой автоподстройки частоты при наличии шума // Автоматика и телемеханика. М., 1997. ╧2. С.118-129.
9. Yoon C.Y., Lindsey W.C. Phase – locked loop performance in the presence of CW interference and additive noise // IEEE Trans. On communications 1982. V. COM -30. N10. PP. 2305-2311.
10. Sarcar B.C. Phase error dynamics of a first order phase-locked loop in the presence of co-channel tone interference and additive noise // IEEE Trans. M., 1900. V. COM-38. ╧ 7. PP. 962-965.
11. Hasan P. Multiple co channel interference effects in a first order phase – locked loop // ETTM., 1994. V. 5. N3. PP. 319-326.
12. Шахтарин Б.И. Статистическая динамика систем синхронизации. М.: Радио и связь, 1998. 488 с.
13. Karsi M.F., Lindsey W.C. Effects of CW interference on carrier tracking // Proc. IEEE Conf. M., 1994. PP. 301-305.
14. Стратонович Р.Л. Избранные вопросы теории флуктуации в радиотехнике. М.: Советское радио, 1961. 210 с.
15. Sarcar B.C. On the joint statistics of amplitude and phase of a signal with co-channel interference // Proc. IEEE. M., 1988. V. 76. N 3. PP. 298-299.
16. Журавлев А.Г. Работа системы фазовой автоподстройки частоты при гармонических помехах// Радиотехника. М., 1963 Т. 18. ╧ 9. С. 38-46.
Публикации с ключевыми словами: статистические характеристики, система синхронизации, прицельная помеха
Публикации со словами: статистические характеристики, система синхронизации, прицельная помеха
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



