научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 02, февраль 2011
ОмГУ им. Ф.М. Достоевского
sbelim@mail.ru
bardichevv@gmail.com
Введение
При хранении информации определяющим фактором является взаимосвязь данных. Правильно выстроенная архитектура размещения информации существенно ускоряет доступ к ней и позволяет выявлять различные закономерности. Большое количество моделей представления данных может быть смоделировано в виде графов. При исследовании графов важную роль играет понятие связности, понимаемое как существование пути из одной вершины графа в другую. Однако в ряде прикладных задач важным становится не только сама достижимость из одной вершины другой вершины, но и длина соответствующего пути. Будем считать, что дуги определяют некоторые взаимодействия или связи между вершинами. Поставим себе задачу нахождения не только непосредственных связей между вершинами, но и связи через посредников, то есть более длинные пути. В качестве приложений данной проблемы можно привести квантовые системы, в которых роль множества вершин играют состояния системы, а множества дуг – переходы между состояниями. При этом, возможны переходы как напрямую между состояниями, так и через цепочку промежуточных состояний. Другим примером является связь между научными работами по одной тематике. Подавляющее количество научных работ основывается на результатах полученных в более ранних работах. Причем авторы отдельно взятой работы могут основываться на результатах других авторов непосредственно, а могут через цепочку промежуточных результатов третьих авторов. Во всех случаях необходимо учитывать два фактора. Во-первых, непосредственная связь существеннее чем связь через посредников, то есть она должна иметь больший вес в задаче. Во-вторых, связи через различных посредников должны складываться, считая, что все посредники равнозначны.
В данной статье рассмотрены две прикладные задачи, приводящие к алгоритмам поиска связей между вершинами графа. Также проведено сравнение различных весовых функций с помощью компьютерного эксперимента. Полученные закономерности использованы для реализации программного комплекса.
1. Постановка задачи
Рассмотрим две системы приводящих к одной и той же задаче поиска на графах. Первая задача ориентирована на поиск связей между информацией, представленной на различных страницах в сети Интернет, вторая связана с оптимизацией базы данных.
Как хорошо известно, непосредственная связь между гипертекстами реализуется с помощью гиперссылок. Построим граф, соответствующий данной задаче. В качестве множества вершин выберем гипертексты, а в качестве дуг гиперссылки. Очевидно, что задача не может быть решена полностью, так как установление всех связей приведет к построению графа, соответствующего всей глобальной сети, что является задачей вычислительно трудноразрешимой. Выбирая отдельно взятый гипертекст, мы можем выявить другие гипертексты, связанные с ним либо непосредственно, либо через промежуточные страницы. Поэтому необходимо вводить ограничение либо по общему количеству рассматриваемых страниц, либо количеству связей, либо по удаленности от заданной вершины. В предлагаемой работе использовался третий подход. Данная задача весьма актуальна, например, при поиске информации, так как позволяет определять не только страницы, содержащие ключевые слова, но и близкие к ним по содержанию. Также предложенная модель позволяет искать исходные документы после многократного тестирования.
При построении баз данных важным является вопрос о связях между таблицами, то есть взаимных ссылках. Две таблицы могут не иметь прямой связи, однако быть сильно зависимыми друг от друга через промежуточные таблицы. В этом случае для ускорения доступа к информации имеет смысл добавлять прямую связь. Для достаточно больших баз данных такая задача весьма актуальна, особенно, если база данных проектировалась изначально не целиком, а наращивалась в процессе работы. Рассмотрение этой системы приводит к той же самой модели, если в качестве вершин графа брать таблицы, а множество ребер будет определяться связями.
2. Модель системы
Пусть граф определен множеством вершин V и множеством дуг D. Отношение инцидентности будем задавать с помощью матрицы смежности E. А именно, если существует дуга из вершины vi в вершину vj, то соответствующий элемент матрицы смешения Eij=1, в противном случае Eij=0. Также будем считать, что в графе нет петель и полагать Eii=0.
Будем считать, что дуги определяют некоторые взаимодействия или связи между вершинами. Поставим себе задачу нахождения не только непосредственных связей между вершинами, но и связи через посредников, то есть более длинные пути. Сформулируем более строгую постановку задачи. Пусть между вершинами vi и vj некоторого графа существует несколько путей длины k. Обозначим количество таких путей через pk(vi,vj). В общем случае будем считать, что пути разной длины дают разный вклад в связь двух вершин. Введем соответствующую функцию g(k), которую в дальнейшем будем называть весовой функцией пути. Более точно g(k) показывает вклад в связь вершин пути длиной k.
Введем величину, называемую в дальнейшем силой связности вершин:

Рассматривая граф, как представление влияния элементов множества V друг на друга, можно сказать, что наличие дуги между вершинами показывает прямое влияние, путь длины 2 – влияние через одного посредника, длины 3 – через двух посредников, и так далее длины n – через n-1 посредника.
Определим матрицу сил связности вершин M, показывающую взаимное влияние всех вершин графа друг на друга:
![]()
Используя алгоритм, предложенный в работе [1] можем записать следующее соотношение:
![]()
Важным является вопрос выбора функции g(k). Рассмотрим свойства, которым должна удовлетворять эта функция:
1. g(1)=1, то есть наличие дуги между двумя вершинами должно давать единичный вклад в силу связности.
2. ![]() , для всех
, для всех ![]() . То есть функция g(k) должна быть убывающей.
. То есть функция g(k) должна быть убывающей.
3. ![]() , для всех
, для всех ![]() . Наличие путей должно увеличивать силу связности.
. Наличие путей должно увеличивать силу связности.
Рассмотрим некоторые возможные варианты выбора функции g(k).
1. ![]() , где
, где ![]() . Функция данного вида была рассмотрена в [2] для выявления связных структур методом построения иерархического дерева. В этом случае сила связности двух вершин вычисляется по формуле:
. Функция данного вида была рассмотрена в [2] для выявления связных структур методом построения иерархического дерева. В этом случае сила связности двух вершин вычисляется по формуле:
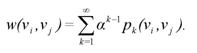
Матрица сил связности имеет вид:

Здесь I – единичная матрица. Коэффициент α имеет двоякий смысл. С одной стороны, он показывает, во сколько раз уменьшается относительное влияние пути при увеличении его длины на единицу. С другой стороны рассмотрим ситуацию, при которой из вершины vi в вершину vj ведет несколько путей одинаковой длины. В частности, если имеется p2(vi,vj)=1/α путей длины 2, то они дают такой же вклад в силу связности, как и дуга между вершинами. При наличии p3(vi,vj)=1/α путей длины 3 их вклад будет эквивалентен одному пути длиной 2. Если же имеется p3(vi,vj)=1/α2 путей длины 3, то их вклад эквивалентен одной дуге. В общем случае при наличии pn(vi,vj)=1/αn-k путей длины n их вклад будет эквивалентен одному пути длины k. Эти соображения позволяют выбирать коэффициент α из практических соображений.
2. ![]() . Сила связности двух вершин будет вычисляться по формуле:
. Сила связности двух вершин будет вычисляться по формуле:

Соответственно матрица сил связности:

В данном случае длинные пути дают значительно больший вклад в силу связности, чем в предыдущем случае. В частности необходимо pn(vi,vj)=n путей длины n, чтобы получить вклад эквивалентный дуге. И, соответственно pn(vi,vj)=n/k путей длины n, чтобы получить вклад эквивалентный пути длиной k.
Нахождение силы связности вершин может применяться для решения двух основных задач:
Частная задача. Нахождение вершин графа наиболее сильно связанных с заданной вершиной. Более строго формулировка задачи сводится к поиску вершин v', метрическая связность которых с данной вершиной v лежит в некотором интервале In:
![]()
При данном подходе существенным является выбор интервала In. Рассмотрим влияние выбора интервала на смысл решаемой задачи для весовой функции ![]() (
(![]() ).
).
Для этого выделим несколько характерных случаев:
In=[1,∞) - позволяет выявить все вершины, связанные с данной вершиной дугами, либо эквивалентные случаи;
In=(1,∞) - позволяет выявить вершины, которые связанны с данной дугой и еще как минимум одним путем;
In=[1+α,∞) - вершины, связанные с v дугой и, как минимум, путем с длиной 2;
In=[1+αn,∞) - вершины, связанные с v дугой и, как минимум, путем с длиной не более n+1;
In=[α,1) - вершины, не связанные дугой с v, но связанные путем длины 2;
In=[α2, α) - вершины, не связанные дугой с v, но связанные путем длины 3;
In= [αn, αn-k) - вершины, не связанные дугой с v, но связанные путем длины не менее k и не более n+1;
В этом случае k путей длины k эквивалентны дуге.
Общая задача. Разбиение графа на связные структуры, то есть поиск подграфов с определенной метрической связностью вершин.
Как и для частной задачи необходимо ввести некоторый интервал значений метрической связности In для вершин входящих в одну связную структуру. Более строго, связной структурой будем называть подмножество вершин V'![]() V, для каждой пары вершин из которого w(v,v')
V, для каждой пары вершин из которого w(v,v') ![]() In, (v,v'
In, (v,v' ![]() V').
V').
Рассмотрим несколько вариантов интервалов In для весовой функции ![]() , (
, (![]() ):
):
In=[1,∞) - позволяет выявить связные структуры, все вершины которых попарно связанны друг с другом дугой, либо эквивалентные случаи;
In=(1,∞) - позволяет выявить связные структуры, все вершины которых попарно связанны друг с другом дугой и еще как минимум одним путем;
In=[1+α,∞) - позволяет выявить связные структуры, все вершины которых попарно связанны друг с другом дугой и, как минимум, путем длины 2;
In=[1+αn,∞) - позволяет выявить связные структуры, все вершины которых попарно связанны друг с другом дугой и, как минимум, путем с длиной не более n+1;
In=[α,1) - позволяет выявить связные структуры, все вершины которых попарно не связанны друг с другом дугой, но связанные путем длины 2;
In= [α2,α) - позволяет выявить связные структуры, все вершины которых попарно не связанны друг с другом дугой, но связанные путем длины 3;
In= [αn,αn-k) - позволяет выявить связные структуры, все вершины которых попарно не связанны друг с другом не связанные дугой с v, но связанные путем длины не менее k и не более n+1.
3. Компьютерный эксперимент
Компьютерный эксперимент ставился с целью сравнения результатов, получаемых при различных весовых функциях g(k). Исследовались ориентированные графы с количеством вершин равным 100 и некоторым определенным количеством дуг d.
Матрица смешения задавалась случайным образом. Во всех экспериментах генерировалось 100 матриц, после чего производилось
усреднение. Матрица связности вычислялась с точностью до третьего слагаемого:
![]()
На рисунке 1 по оси абсцисс отложена величина метрической связности, а по оси ординат количество соответствующих связей.

Рис. 1. Решение частной задачи для весовой функции ![]() (α=0.1)
(α=0.1)
На рисунках 2 и 3 представлены аналогичные графики для весовой функции g(k)=1/k и d=500(рис. 2) и d=3000 (рис. 3).

Рис. 2. Решение частной задачи для весовой функции g(k)=1/k, d=500.
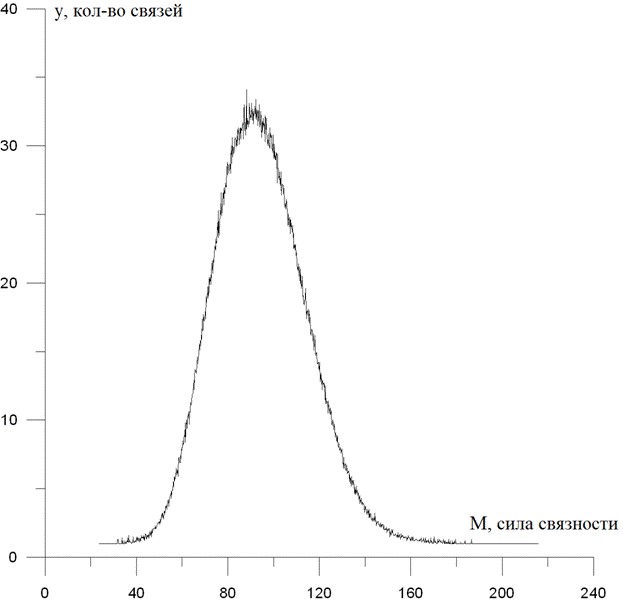
Рис. 3. Решение частной задачи для весовой функции g(k)=1/k, d=3000.
Как хорошо видно, в случае весовой функции g(k)=1/k присутствует пик связностей определенной величины. Это обстоятельство
делает данный вид весовой функции малопригодным для исследования графов в реальных задачах. Напротив, использование весовой функции![]() приводит к адекватному поведению графиков. А именно, чем больше величина метрической связности, тем меньше соответствующее количество связей. Попытки получения точного результата по формуле
приводит к адекватному поведению графиков. А именно, чем больше величина метрической связности, тем меньше соответствующее количество связей. Попытки получения точного результата по формуле

наталкиваются на трудности, связанные с наличием ориентированных циклов, и как следствие с многократным учетом одних и тех же путей.
Заключение
Таким образом, компьютерный эксперимент показал, что степенная функция обладает более подходящими свойствами для использования в качестве весовой при поиске связей на графе. Поиск же самих связей может быть произведен за полиномиальное время.
Программный комплекс поиска связанных страниц, реализованный на базе построенной модели получает на входе адрес станицы в Интернет и, просматривая гиперссылки, осуществляет переход по ним на заданную глубину. В результате строится граф, задаваемый матрицей смешения, для которого и ищутся связанные вершины. Результатом работы является список сайтов с указанием меры связности с заданной страницей.
Использование разработанного программного комплекса, позволяет, например, выявлять наиболее сильно связанные понятия в электронной энциклопедии «wikipedia» или искать связанные научные статьи на некоторых сайтах научных журналов, например, таких как Physical Review.
Авторы выражают благодарность Н.Ф.Богаченко за полезные обсуждения постановки задачи и используемой терминологии.
Литература
1. Girvan M., Newman M.E.J. Community structure in social and biological networks
// arXiv:cond-mat/0112110v1.(2001)
2. Newman M.E.J. Mixing patterns in networks // Phys. Rev. E. 2003. V.67. P. 026126-1 -026126-13.
Публикации с ключевыми словами: взаимосвязь данных, алгоритм поиска связей, граф доступа
Публикации со словами: взаимосвязь данных, алгоритм поиска связей, граф доступа
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



