научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 02, февраль 2011
УДК 658.51
info@rk9.bmstu.ru
МГТУ им. Н.Э. Баумана
Успешность производственно-хозяйственной деятельности современных предприятий, работающих в условиях высокой динамики деловой среды, во многом зависит от их производственной гибкости и от их способности к формированию оптимальных стратегий использования имеющихся производственных ресурсов, ориентированных на оперативное выполнение текущих заказов. Решение этой проблемы может базироваться на рациональном структурировании производственных процессов, обеспечивающем достижение максимальной производительности производственно-технологического комплекса ПТК). Один из подходов к такому структурированию обсуждается в настоящей работе.
Структура производственного процесса, реализуемого на заданной системе исполнительных средств, может быть адекватно описана потоковой сетевой моделью класса «направленная сеть» (далее – «сеть»). В фундаментальных работах по сетевым методологиям [1, 2], сеть N=EÈA определена, как связный ориентированный взвешенный граф, являющийся совокупностью множества элементов E={x1, х2, … хе … хЕ} и множества упорядоченных пар элементов A={… (xе, хе+1), ...}, которые нагружены весовой функцией F={f(xе, хе+1)}.
Рассмотрим задачу о максимальном сетевом потоке в следующей постановке [3]. Задана направленная сеть, на которой исследуется процесс, моделируемый потоком FN, переносящим по сети некоторые абстрактные элементы потока. Поток сети перемещается из вершины-источника s сети к вершине-стоку t через промежуточные вершины x1, х2,…хе… по дугам сети (xе, хе+1). Множество дуг сети А нагружено двумя весовыми функциями - функцией величины текущего потока на дугах сети F={f(xе, хе+1)} |" (xе, хе+1)ÎА и функцией пропускной способности дуг сети L={l(xе, хе+1)} |" (xе, хе+1)ÎА. Требуется определить такую конфигурацию функции текущего потока на множестве дуг сети F={f(xе, хе+1)}, при которой общий поток сети достигает максимального значения maxFN.
Рассмотрение задачи о максимальном сетевом потоке в контексте проектирования технологических процессов, предполагает следующую производственную интерпретацию основных элементов сетевой семантики. Сеть моделирует техпроцесс, заданный как множество операций, преобразующих предмет труда из состояния «заготовка» в состояние «деталь». Дуги сети обозначают операции техпроцесса, а вершины сети – пограничные события «завершение предшествующей операции техпроцесса и начало следующей операции». Исток сети – это событие «начало производственного цикла», заданного техпроцессом, а сток сети – событие «окончание производственного цикла». Величина потока дуги задаёт текущую производительность рассматриваемой операции техпроцесса, а пропускная способность дуги – максимально возможную производительность данной операции. Поток сети является параметром, который характеризует производительность рассматриваемого ПТК.
Сформулированная выше постановка задачи о максимальном сетевом потоке требует выполнения базовых ограничений, установленных синтаксисом теории графов, а также, введения дополнительных ограничений, обеспечивающих адаптацию базовой сетевой задачи к специфике рассматриваемого нами технологического аспекта. Ограничения синтаксиса теории графов (1) предъявляют к потокам сети требования стационарности, ограниченности, баланса входящих и исходящих потоков на дугах, инцидентных промежуточным вершинам сети, а также равенства сетевого потока сумме потоков на дугах инцидентных вершине-источнику и на дугах инцидентных вершине-стоку.

Дополнительные ограничения (2) требуют, чтобы сеть была двухполюсной и, чтобы дуги сети обладали односторонней проводимостью.
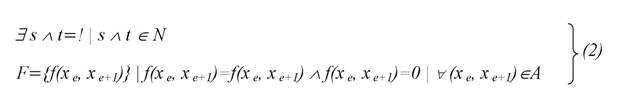
Искомым результатом сетевого моделирования является определение величины максимально достижимого потока в заданной сети (3):

Вид систем (1), (2) и уравнения (3) показывает, что формализованные нами начальные условия рассматриваемой сетевой потоковой задачи складываются из компонент, идентичных типовым компонентам оптимизационной задачи линейного программирования [4], в контексте которой зависимость (3) играет роль целевой функции, а условия (2) и (3) – роль системных ограничений.
Таким образом, задача о максимальном сетевом потоке, как инструмент формирования рационального техпроцесса для заданной системы исполнительных средств, может быть приведена к задаче линейного программирования. Это позволяет аналитически формализовать её решение и делает такое решение доступным для широкого круга специалистов. Автоматизация данного проектного процесса также не представляет технических затруднений, так как метод линейного программирования является стандартным приложением ряда распространённых программных продуктов (например, MS Excel), а также доступен для решения в среде вычислительных программных продуктов (MathCAD и др.).
Практическое применение предлагаемого подхода можно показать на примере решения следующей простой задачи.
1. Исходные данные
Требуется спроектировать процесс изготовления детали (табл. 1) для заданного участка механообработки (табл. 2). Заказ должен быть выполнен в максимально короткий срок, для чего должны быть использованы все располагаемые производственные ресурсы участка.
Обрабатываемая деталь Таблица 1
Чертёж детали | Требования к детали | ||||
Поверхность детали | IT | Ra | |||

| Поверхность 7 | 7 | 1 | ||
Остальные поверхности | 9 | 3,2 | |||
Участок механообработки Таблица 2
Станочный парк участка механообработки | Производительность * |
Группа токарных станков (Т.ст) | 8 дет/час |
Группа сверлильных станков (С.ст) | 6 дет/час |
Группа фрезерных станков (Ф.ст) | 4дет/час |
Группа шлифовальных станков (Ш.ст) | 12 дет/час |
Группа фрезерно-сверлильных станков (ФС.ст) | 3 дет/час |
Группа токарно-фрезерно-сверлильных станков (ТФС.ст) | 5 дет/час |
* Максимальная производительность группы станков при обработке заданной детали
Для решения поставленной задачи необходимо проанализировать исходные данные и интерпретировать рассматриваемую производственную ситуацию в понятиях сетевой модели, математически формализовать условия оптимизационного решения сформированной задачи методом линейного программирования и найти её решение.
2. Анализ исходных данных
Целью анализа исходных данных является формирование множества возможных технологических маршрутов, которые могут быть применены для изготовления детали на заданном участке. В рассматриваемом нами случае, ограничения, обусловленные требованиями к точности и к шероховатости обрабатываемых поверхностей изготавливаемой детали, позволяют определить [5] возможные методы обработки её поверхностей (табл. 3). Опираясь на эти данные, а также, учитывая форму обрабатываемых поверхностей детали и технологическую специализацию имеющегося парка станков, можно предложить три возможных варианта технологического маршрута обработки заданной детали (табл.4).
Методы обработки детали Таблица 3.
Требования | Метод обработки детали | Обрабатываемая поверхность детали | ||
IT9, Ra3,2 | Лезвийная обработка | Черновая à Получистовая à Чистовая | 1, 2, 3, 4, 5, 6, 7, 8, 9 | |
Финишная | Тонкое точение | 7 | ||
IT7, Ra1 | Абразивная обработка | Чистовое шлифование | ||
Варианты маршрутов обработки детали на заданном участке Таблица 4.
╧ вар. | Технологический маршрут обработки* | Метод механической обработки** | |||
Т | Ф | С | Ш | ||
Обрабатываемые поверхности детали | |||||
1 | Т.ст - Ф.ст - С.ст – Ш.ст | 1, 2, 5, 6, 7, 9 | 2, 8 | 4 | 7 |
2 | Т.ст – ФС.ст – Ш.ст | 2, 8, 4 | |||
3 | ТФС.ст | 1, 2, 3, 4, 5, 6, 7, 8, 9 | |||
* Аббревиатуры групп станков, на которых производится обработка приведены в табл. 1.
** Аббревиатуры методов механической обработки детали: Т – токарная, Ф – фрезерная; С – сверлильная: Ш – шлифовальная.
Учитывая требование о максимально коротком сроке выполнения заказа, необходимо использовать для обработки детали всю производственную мощность участка. Для этого следует параллельно задействовать все три технологических маршрута, рационально распределив их технологические потоки между станками участка.
3. Интерпретация рассматриваемой производственной задачи в понятиях сетевой модели
Совокупность возможных маршрутов обработки детали описывается сетью (рис. 1), в которой дуги символизируют выполнение отдельных стадий механической обработки детали на группах станков с однородной технологической специализацией. Весовые параметры дуг задают максимально возможную производительность однородных групп станков и их искомую (текущую) производительность. Искомая производительность должна обеспечивать такое распределение технологических потоков, при котором общий поток сети будет максимальным и заказ будет выполнен в кратчайший срок.

В данной сетевой модели каждый из возможных параллельно выполняемых технологических маршрутов описывается своим сквозным st-путём:
Маршрут1 : Т.стàФ.стàС.стàШ.ст ≡ st-путь: (s,x1)à(x1,x3)à(x3,x2)à(x2,t)
Маршрут 2: Т.стàФС.стàШ.ст ≡ st-путь: (s,x1)à(x1,x2)à(x2,t)
Маршрут 3: ТФС.ст ≡ st-путь: (s,t)
4. Приведение условий сформулированной задачи к оптимизационной задаче линейного программирования
При решении сформулированной выше сетевой задачи методом линейного программирования, начальные условия задачи формально задаются целевой функцией (4) и системой ограничительных условий (5) :
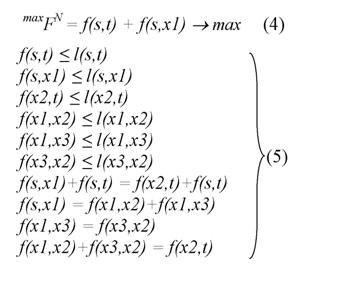
5. Решение рассматриваемой задачи, как задачи линейного программирования
Для решения рассматриваемой задачи методом линейного программирования используются начальные условия, в которых целевая функция (4) и ограничения (5) конкретизируются заданными значениями пропускной способности дуг направленной сети. Задача решается симплекс-методом «вручную» или «автоматизировано». Результаты, полученные при «автоматизированном» решении рассматриваемой задачи методом линейного программирования в среде MS Excel, приведены на рис. 2.
Таким образом, при заданных условиях, максимальный технологический грузопоток, обеспечивающий выполнение заказа в кратчайший срок, реализуется маршрутной технологической схемой, описанной в таблице 5.
Результаты решения задачи Таблица 5.
╧ п.п. | Параметры сети | Дуги сети ≡ Технологические группы станков | |||||
(s,t) ТФС.ст | (s,x1) Т.ст | (x1,x2) ФС.ст | (x1,x3) Ф.ст | (x3,x2) С.ст | (x2,t) Ш.ст | ||
1. | Потоки на дугах сети f(x е, x е+1) ≡ Производительность групп станков, дет/час | 5 | 7 | 3 | 4 | 4 | 7 |
2. | Максимальный поток сети maxFN ≡ Производительность участка, дет/час | 12 | |||||
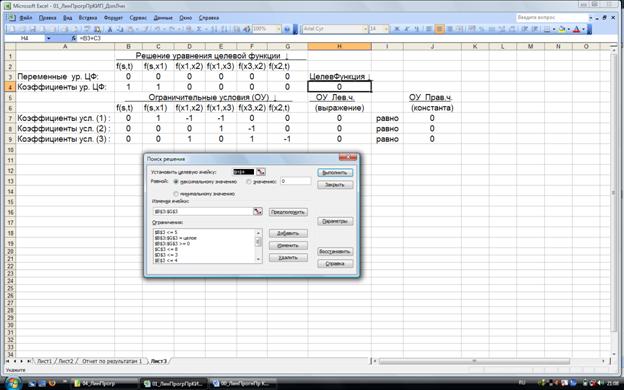

Рис. 2. Результаты решения задачи.
Полученные результаты определяют комплексную топологию технологических маршрутов предлагаемого производственного процесса, а также, - рекомендуемое распределение производственных потоков предмета труда между технологически специализированными группами станков участка (рис. 3), обеспечивающее максимальную производительность ПТК при выполнении срочного заказа по изготовлению рассматриваемой детали.
|
Рассмотренный пример показывает, как обсуждаемая методология позволяет сформировать принципиальное решение исследуемой проблемы и как с её помощью выявляется оптимальная топология технологической структуры проектируемого производственного процесса.
Заключение
Рассмотренные выше материалы позволяет сделать следующие основные выводы.
1. Задача формирования технологических процессов, рационально реализуемых на заданной системе исполнительных средств ПрС, является актуальным вопросом технологической подготовки гибких производственных систем.
2. Решение данной задачи может опираться на математические методы оптимизации сетевых потоков, в частности, - на решение задачи о максимальном сетевом потоке.
3. Интерпретация производственной задачи в понятиях потокового сетевого моделирования и анализ начальных условий сетевой модели показывает, что задача о максимальной производительности ПТК приводится к задаче линейного программирования. Это позволяет формализовать решение рассмотренной производственной задачи и делает такое решение доступным для широкого круга практикующих специалистов.
СПИСОК ЛИТЕРАТУРЫ
1. | Ford L.R., Fulkerson D.R. Flows in networks. Princeton, New Jersey: Princeton University Press, 1962. 276 р. |
2. | Edward Minieka. Optimization Algorithms for Networks and Graphs. New York and Basel: Marcel Dekker, Inc., 1978. 323 р. |
3. | Омельченко И.Н., Лазаренко А.Г. Графоаналитическое решение логистической задачи о максимальном сетевом потоке минимальной стоимости // Вестник машиностроения. 2007, ╧9. С. 71-73. |
4. | Волков И.К., Загоруйко Е.А. Исследование операций. М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. 430 с. |
5. | Кондаков А.И., Островский Ю.А. Разработка маршрутных технологических процессов изготовления деталей. М.: Изд-во МГТУ им. Н.Э. Баумана, 2003. 50 с. |
Публикации с ключевыми словами: рациональный технологический маршрут обработки детали, гибкая производственная система
Публикации со словами: рациональный технологический маршрут обработки детали, гибкая производственная система
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||




