научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 02, февраль 2011
УДК. 334.7.
МГТУ им. Н.Э. Баумана, НИУ-ВШЭ
Введение
Одна из важнейших тенденций современного этапа познания мира, окружающего нас и в том числе создаваемого нами, состоит в стремлении к трансдисциплинарности. Это означает, что наше познание стремится выйти за традиционные рамки отдельных научных дисциплин. Разумеется, дело здесь не ограничивается прямым заимствованием тех или иных конкретных методов исследования (например, физических методов в биологии или математических в экономике). Речь идет о поиске наиболее глубоких общенаучных концепций, объединяющих естественные и гуманитарные науки и образующих единый язык рационального научного познания [4].
В свое время в рамках неклассического подхода возникло осознание того факта, что, по существу, все описываемые наукой объекты являются сложными и открытыми. Это означает, что мы не можем полностью пренебречь ни внутренними (как правило, нелинейными) взаимодействиями частей объекта друг с другом, ни внешними (как правило, случайными) воздействиями на этот объект со стороны его окружения. Сложность объекта может привести его - и во многих случаях приводит - к состоянию динамического хаоса, тогда как открытость объекта порождает энтропийный дисбаланс, приводящий, в зависимости от конкретных условий, либо к деградации, либо к упорядочению объекта.
В результате взаимодействия системы со средой, когда ее флуктуации усиливаются, они постепенно расшатывают старый порядок и структуру. Однако конечный результат их взаимодействия на систему не является однозначно определенным или детерминированным. В критической точке, точке бифуркации, открываются, по крайней мере, две возможности для дальнейшей эволюции системы [1,19]. Какой путь при этом будет «выбран» системой, зависит от случайных обстоятельств и факторов, складывающихся в окрестности точки бифуркации. Поэтому поведение системы в этой точке нельзя предсказать с полной достоверностью. Но когда определенный путь будет выбран, тогда дальнейшее движение системы починяется детерминистическим законам до следующей бифуркации. При этом, случайные события, факторы и обстоятельства также взаимодействуют друг с другом, и поэтому их результат оказывается непредсказуемым. Только когда установится определенный динамический режим и сформируется новая траектория движения, эволюция системы на макроуровне приобретает детерминистический характер. Однако это продолжается до тех пор, пока не возникнут новые флуктуации, усиление которых приведет к неустойчивости прежней системы, а затем и к замене ее структуры новой.
Неопределенность внутренне присуща любой практической деятельности человека и в системных задачах выступает в качестве ограничительного фактора на этапах исследования, создания и совершенствования моделей систем и их компонентов. Из-за действия неопределенности вероятность определенных последствий в природе невозможно предсказать с достаточной степенью точности. «И всюду, вместе с необходимостью, проявляется возможное, вероятное, многообразное, вследствие чего лишь некоторые альтернативы, благодаря действую отбора становятся действительностью. Считается, что наивысшим потенциалом неопределенности обладают социально-экономические среды [9].
Моделирование неопределенности, установление важности и значимости ее влияния на наши подходы, решения и действия независимо от природы и источника ее возникновения становится важной задачей и возможно в рамках теории случайных процессов.
Моделирование неопределенности в рамках теории случайных процессов
Греческое слово «стохос» означает предположение, догадка. В теории случайных процессов рассматриваются модели, когда состояние X(t)=f(t0, t, w), где f – некоторая случайная функция. Как отмечают А.А. Петров, И.Г. Поспелов, А.А. Шананин «в любой социально-экономической системе у людей достаточно свободы, чтобы действия их всех вместе выглядели хаотичными» [6].
Теория случайных процессов является одной из наиболее развивающихся областей теории вероятности. Развитие теории вероятности как самостоятельной науки началось с переписки Паскаля и Ферма в 1654 году, хотя значительно раньше этих ученых многие математики занимались задачами, относящимися к азартным играм. Само понятие вероятности восходит к древним временам; оно было известно уже античным философам, в частности Платону. Мысль о том, что законы природы проявляются через множество случайных событий, впервые возникла у древнегреческих материалистов. Ее подробное изложение дано в поэме Лукреция Кара «О природе вещей», важнейшие отрывки из которой цитируются в беседе Паскаля и Митона (и в примечаниях), приводимой в четвертом письме.
Следующий период истории исследования теории вероятностей (конец 18 и начало 19 в.) связан с именами А. Муавра (Англия), П. Лапласа (Франция), К. Гаусса (Германия) и С. Пуассона (Франция). Это период, когда теория вероятности уже находит ряд весьма актуальных применений в естествознании и технике (главным образом в теории ошибок наблюдений, развившейся в связи с потребностями геодезии и астрономии, и в теории стрельбы). К этому периоду относится доказательство первых предельных теорем, носящих теперь названия теорем Лапласа (1812) и Пуассона (1837); А. Лежандром (Франция, 1806) и Гауссом (1808) в это же время был разработан способ наименьших квадратов.
Третий период истории исследования теории вероятностей (2-я половина 19 в.) связан в основном с именами русских математиков П. Л. Чебышева, А. М. Ляпунова и А. А. Маркова (старшего). Теория вероятностей развивалась в России и раньше (в 18 в. ряд трудов работавших в России Л. Эйлером, Н. Бернулли и Д. Бернулли; во второй период развития теории вероятностей следует отметить работы М. В. Остроградского по вопросам теории вероятностей, связанным с математической статистикой, и В. Я. Буняковского по применению теории вероятностей к страховому делу, статистике и демографии). Со 2-й половины 19 в. исследования по данному вопросу в России занимают ведущее место в мире. Чебышев и его ученики Ляпунов и Марков поставили и решили ряд общих задач в теории вероятностей, обобщающих теоремы Бернулли и Лапласа. Чебышев доказал (1867) закон больших чисел при весьма общих предположениях. Он же впервые сформулировал (1887) центральную предельную теорему для сумм независимых случайных величин и указал один из методов её доказательства. Другим методом Ляпунов получил (1901) близкое к окончательному решение этого вопроса. Марков впервые рассмотрел (1907) один случай зависимых испытаний, который впоследствии получил название цепей Маркова.
В Западной Европе во 2-й половине 19 в. получили большое развитие работы по математической статистике (в Бельгии - А. Кетле, в Англии - Ф. Гальтон) и статистической физике (в Австрии - Л. Больцман), которые наряду с основными теоретическими работами Чебышева, Ляпунова и Маркова создали основу для существенного расширения проблематики теории вероятностей в четвёртом (современном) периоде её развития. Этот период истории исследования данной теории характеризуется чрезвычайным расширением круга её применений, созданием нескольких систем безукоризненно строгого математического обоснования теории вероятностей, новых мощных методов, требующих иногда применения (помимо классического анализа) средств теории множеств, теории функций действительного переменного и функционального анализа.
В этот период при очень большом усилении работы по теории вероятностей за рубежом (во Франции - Э. Борель, П. Леви, М. Фреше, в Германии - Р. Мизес, в США - Н. Винер, В. Феллер, Дж. Дуб, в Швеции - Г. Крамер) советская наука продолжала занимать значительное, а в ряде направлений и ведущее положение. В Советской России новый период развития теории вероятностей открывался деятельностью С. Н. Бернштейна, значительно обобщившего классические предельные теоремы Чебышева, Ляпунова и Маркова и впервые в России широко поставившего работу по применению теории вероятностей к естествознанию. В Москве А. Я. Хинчин и А. Н. Колмогоров начали с применения к вопросам теории вероятностей методов теории функций действительного переменного. Позднее (в 30-х гг.) они (и Е. Е. Слуцкий) заложили основы теории случайных процессов.
В начале ХХ века французский финансист Л. Башелье предложил рассматривать эволюцию стоимостей акций на парижском рынке как случайный процесс. А. Эйнштейн точно таким же случайным процессом описал броуновское движение взвешенных частиц в жидкости. Систематическому обобщению теория случайных процессов впервые подверглась в статье А.Н. Колмогорова. Хотя истоки теории случайных процессов лежали в области экономики, после Л. Башелье большинство ее методов разрабатывалось и использовалось в области теоретической физики.
В 20-х гг. 20 в. было обнаружено, что даже в схеме последовательности одинаково распределённых и независимых случайных величин могут вполне естественным образом возникать предельные распределения, отличные от нормального. Механизм возникновения большинства предельных закономерностей может быть до конца понят лишь в связи с теорией случайных процессов.
Марковские случайные процессы
Марковские случайные процессы названы по имени выдающегося русского математика А.А.Маркова (1856-1922), впервые начавшего изучение вероятностной связи случайных величин и создавшего теорию, которую можно назвать "динамикой вероятностей". Случайный процесс Х (t) называется марковским, если для любых двух моментов времени t0 и t1 (t0 < t1) условное распределение вероятностей X (t1) при условии, что заданы все значения Х (t) при t < t0, зависит только от X (t0) (в силу этого Марковские случайные процессы иногда называют процессами без последействия). Марковские процессы являются естественным обобщением детерминированных процессов. В детерминированных процессах состояние системы в момент времени t0 однозначно определяет ход процесса в будущем; в Марковских процессах состояние системы в момент времени t0 однозначно определяет распределение вероятностей хода процесса при t > t0, причём никакие сведения о ходе процесса до момента времени t0 не изменяют это распределение.
Таким образом, процесс, протекающий в экономической системе, называется Марковским, если в любой момент времени вероятность любого состояния системы в будущем зависит только от состояния системы в текущий момент и не зависит от того, каким образом система пришла в это состояние.
Марковские модели нашли широкое применение в задачах управления. Они составляют основу современного арсенала вероятностных методов применительно к описанию состояний управляемого объекта и процесса перехода из одного состояния в другое с течение времени с приемлемой степени точности и достоверностью.
Основные свойства Марковских процессов можно представить следующим образом [8]:
- исходная задача управления стохастической системой погружается в семейство динамических оптимизационных задач, каждый этап управления имеет свою задачу принятия оптимального решения;
- множество решений оптимизационных задач описывается функциональным уравнением динамического программирования;
- оптимальные решения находятся с помощью обратного хода алгоритма, представляющего собой упорядоченную процедуру обработки данных как результатов решения последовательности функциональных уравнений;
- оптимальное управление обладает тем свойством, что каковы бы ни были начальное состояние и решение, принимаемое в этом состоянии, последующие решения образуют оптимальную политику для того этапа, который возникает после первых решений и следовательно переходов.
На наш взгляд, на основе стохастического подхода с использованием цепей Маркова возможно изучение целого ряда аспектов, касающихся деятельности сетевых форм организации бизнеса. В данной работе мы представим, как может быть использован данный подход для изучения доходности индустриальных сетей.
Индустриальные сети как новая форма организации
Новые формы коммерческих организаций, придающие особое значение установлению партнерских отношений, стали неотъемлемой частью экономического ландшафта. Среди них особое место занимают сетевые формы организации, в управлении которыми особое значение придается установлению партнерских отношений между постоянно взаимодействующими, командной работе членов организации, не исключающей участия сотрудников конкурирующих фирм; распределению ответственности за разработку технологий [10]. Разнообразие подобных форм довольно значительно [12, 13, 15, 16, 18, 20]. Различные авторы относят к ним научно-исследовательские коалиции, соглашения о совместном производстве, консорциумы и совместные предприятия, деловые и франчайзинговые сети, стратегические альянсы и другие формы межфирменного сетевого взаимодействия, в которых трансакции планируются и управляются на основе согласованных в процессе взаимодействия правил.
Такого рода новые формы индустриальных образований обеспечивают участникам снижение рисков неопределенности операций, сокращение транзакционных издержек, экономию на масштабах производства, для них характерны гибкость, специализация и значительный акцент на управление взаимоотношениями и связями. Вместе с тем, они требуют определенных усилий по созданию, поддержанию, развитию сети взаимодействия, увеличивают значимость координации деятельности самостоятельных партнеров.
Гибкость сетей дает наибольшие преимущества в современных условиях, когда продукция фирмы (товары, услуги) становятся все сложнее и осуществление прямого контроля над всеми необходимыми ресурсами (в первую очередь знаниями и умением персонала, «ноу-хау») – все затруднительнее, а внешняя среда отличается высокой степенью неопределенности.
Важнейшей задачей для организаций становится выстраивание компанией множества цепочек ценностей, в которых организовано взаимодействие разработчиков, поставщиков, потребителей и третьих сторон для создания инновационных продуктов. Эти цепочки ценности выстраиваются в общую схему инновационных потоков, пронизывающих организацию. В результате границы организации как экономического агента размываются [5]. Можно отметить следующие характерные особенности таких организаций:
- организационная модель хозяйствующего субъекта влияет на модели ее поставщиков и заказчиков;
- постоянное обновление организационной модели само по себе рассматривается как важная инновационная задача;
- внешние партнеры берут на себя часть рисков и прибылей, наравне участвуют в инновационном процессе;
- хозяйствующий субъект управляет интеллектуальной собственностью как стратегическим активом, помогающим выходить на новые для нее рынки.
В результате внедрения открытой организационной модели компания встраивается в сеть инноваций, формируя рынки открытых инноваций, основанные на сетевых межорганизационных структурах.
Управление доходностью в индустриальных сетях
Очевидно, что индустриальные сети играют значительную роль в повышении эффективности производства высокотехнологичных изделий. Однако изучение практики указывает, что формирование альянсов и стратегических сетей ведёт к росту трансакционных и производственных издержек в краткосрочном периоде, но даёт основания рассчитывать на существенные выгоды в средне- или долгосрочной перспективе. Сетевое взаимодействие теряет свои преимущества, если оно обеспечивает создание добавленной стоимости при таком росте издержек, которые наносят ущерб суммарной конкурентоспособности взаимодействующих компаний или при отсутствии механизма перераспределения выгод между всеми участниками сети, препятствующего развитию стимулов к оппортунистическому поведению [11]. Соответственно, предприятия-партнеры индустриальных сетей рассчитывают на получение большего дохода, чем, если бы они действовали в одиночку.
Потребность в современных методах управления доходностью в промышленных сетях весьма актуальна. Сосредоточение внимания руководства на экономической целесообразности принятия решений на каждом этапе реализации проекта позволит не только сэкономить ресурсы, но и обеспечит запланированный уровень доходности.
Движущей силой объединения хозяйствующих субъектов является возможность получения каждым из участников дополнительной выгоды от него. Дополнительная выгода может выражаться в стабилизации финансово-хозяйственного положения, повышении объема производства, снижении затрат на НИОКР; повышении квалификации сотрудников, решении социально-экологических проблем, повышении эффективности использования ресурсов, т.е. в получении дополнительного дохода.
Любой хозяйствующий субъект имеет цели, для достижения которых он создается.
Пусть Еi – эффективность i-го (i=1,…..N) хозяйствующего субъекта до вступления в сеть, а Еis – его же эффективность после вступления в индустриальную сеть. Тогда показатель ![]() представляет собой общую эффективность хозяйствующих субъектов до взаимодействия в индустриальной сети, а
представляет собой общую эффективность хозяйствующих субъектов до взаимодействия в индустриальной сети, а ![]() - их общую эффективность после вступления в сеть по форме s. Очевидно, что взаимодействие имеет смысл при Еs>E, что является необходимым условием интеграции. Полученную от интеграции дополнительную общую эффективность обозначим через ∆Еsобщi, причем она будет складываться из долей ∆Еsобщi каждого хозяйствующего субъекта, входящего в сеть:
- их общую эффективность после вступления в сеть по форме s. Очевидно, что взаимодействие имеет смысл при Еs>E, что является необходимым условием интеграции. Полученную от интеграции дополнительную общую эффективность обозначим через ∆Еsобщi, причем она будет складываться из долей ∆Еsобщi каждого хозяйствующего субъекта, входящего в сеть:
![]()
Следовательно, требование i-го хозяйствующего субъекта получить свою дополнительную эффективность от участия в сети по форме s будет иметь вид:
![]() ,
,
что представляет собой достаточное условие интегрирования предприятия в сеть.
Таким образом, превышение общей эффективности работы хозяйствующих субъектов после формирования сети над тем же показателем до интеграции, а также соблюдение этого условия для показателя эффективности каждого хозяйствующего субъекта в отдельности, являются необходимым и достаточным условиями для устойчивости индустриальной сети [7].
Стратегической целью работы индустриальной сети является максимизация дохода в системе:
I= (IА+IB+IС+…..+IN)= (kAI+kBI+kCI+…….kNI)→max,
где I – общий прогнозируемый доход участников промышленной сети; IА, IВ, IС, ……IN – доли дохода, распределяемые между партнерами соответственно их вкладам в индустриальную сеть; kA, kB, kC,…..kN – весовые коэффициенты, отражающие процент потенциального дохода, полагающийся каждому из участников.
Поскольку цель индустриальных сетей определена как максимизация дохода, то целевая функция будет выглядеть следующим образом:
Ii=(Gi - Ci) *Ni→max,
где Gi - выручка от реализации i-го вида продукции; Ci – совокупные затраты на производство i-го вида продукции; Ni – объем сбыта i-го вида продукции.
Схема функционирования промышленной сети представлена на рис. 1.
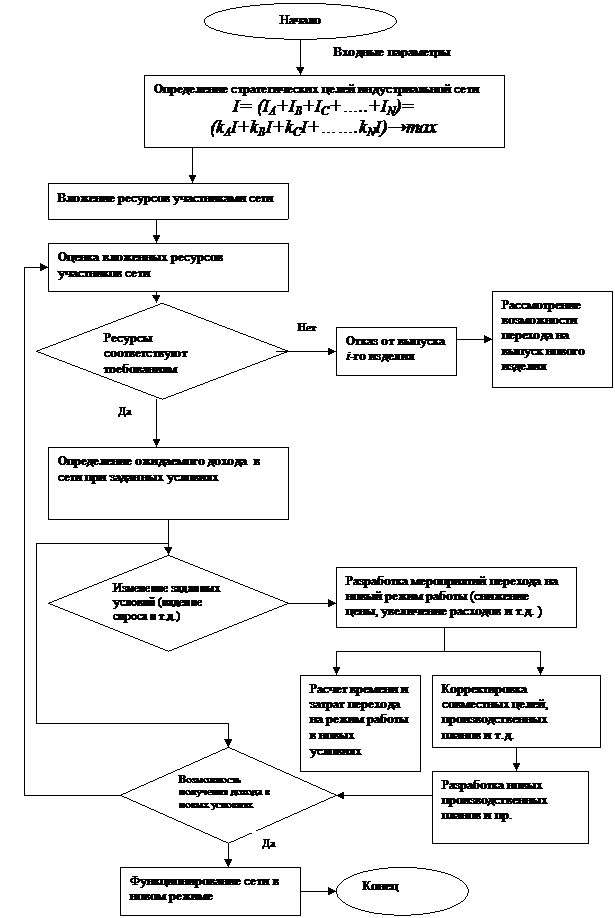
Рис.1. Схема функционирования индустриальной сети
Однако сложность управления доходностью в промышленных сетях заключается в том, что в промышленных сетях на уровень ожидаемого дохода влияют множество внешних и внутренних факторов.
Очевидно, что при разработке решений и управлении сложными системами всегда приходится учитывать неопределенность и риск, обязательно допуская при этом некоторые закономерности вероятностного характера с целью учета роли единичных или массовых случайных явлений. Управленческие решения при этом принимаются в условиях неопределенности, когда невозможно оценить вероятность потенциальных результатов. Это должно иметь место, когда требующие учета факторы настолько сложны и многообразны или новы, что на счет них невозможно получить достаточно релевантной информации. В итоге вероятность или шанс определенного последствия невозможно предсказать с достаточной степенью достоверности.
Неопределенность особенно характерна для тех решений, которые приходится принимать в быстро меняющихся обстоятельствах. Уменьшить неопределенность возможно двумя способами: либо попытаться получить дополнительную релевантную информацию и еще раз проанализировать проблему; либо действовать в точном соответствии с прошлым опытом, суждениями или интуицией и сделать предположение о вероятности событий, когда не хватает времени на сбор дополнительной информации или затраты на нее чересчур высоки.
А значит, разработка моделей управления доходностью в промышленных сетях возможна в рамках стохастического подхода.
Стохастический подход к управлению доходностью в индустриальных сетях
Управление доходностью при межфирменном взаимодействии можно представить как процесс, для которого характерна случайность и наличие обратных связей. Подобные процессы рассматриваются с позиции неравновесности и нелинейности. Когда накапливаются многочисленные случайные отклонения, под их влиянием система входит в состояние качественного изменения, при котором старые сложившиеся связи утрачивают свою силу и будущие изменения становятся многовариантными и непредсказуемыми [2].
Таким образом, сложность объекта управления может привести его (и во многих случаях приводит) к состоянию динамического хаоса, тогда как открытость системы порождает энтропийный дисбаланс, приводящий, в зависимости от конкретных условий, либо к деградации, либо к упорядочению объекта. А, следовательно, управление доходностью при межфирменном взаимодействии как сложного процесса может быть определено вероятностными методами. Основным признаком вероятностной модели является то, что в ней понятия вероятности, необратимости, стохастической динамики и т.п. становятся уже не субъективными свойствами, как в классическом типе рациональности, но вполне объективными, присущими целостному описанию сложных открытых объектов. Роль вероятностных моделей состоит именно в том, что даваемое ими описание является столь же фундаментальным, как и более привычное строго детерминистическое, свойственное, как правило, классическому типу рациональности.
Рассмотрим поведение некоторой управляемой системы, функционирующей в дискретные моменты времени ![]() ,составляющие горизонт планирования и управления. Предположим, что в фиксированный момент времени этого дискретного ряда система может находиться только в одном из m состояний Sj j=1,…..m, причем реализация конкретного состояния зависит от того, в каком состоянии находилась система непосредственно в предшествующий момент времени и только от него.
,составляющие горизонт планирования и управления. Предположим, что в фиксированный момент времени этого дискретного ряда система может находиться только в одном из m состояний Sj j=1,…..m, причем реализация конкретного состояния зависит от того, в каком состоянии находилась система непосредственно в предшествующий момент времени и только от него.
Из теории случайных процессов известно, что если x(t) – некоторый случайный процесс, характеризующий состояние или поведение управляемой системы, то последовательность случайных величин ![]() k=0,1,…N, характеризует стохастический процесс в системе в дискретные моменты времени tk, k=0,1,…..N.
k=0,1,…N, характеризует стохастический процесс в системе в дискретные моменты времени tk, k=0,1,…..N.
Пусть имеется система Sj с дискретными состояниями S1, S2 , S3 . Состояния отражают возможный исход реализации проекта и переход системы в одно из состояний:
S1 – доходность в сети осталась без изменений
S2 – доходность в сети увеличилась
S3 – доходность в сети снизилась
Предположим, что случайные переходы происходят в определенные моменты времени t0, t1, t2…, составляющие период планирования и управления. Эти моменты будем называть шагами процесса: t0 = 0 – его началом. Сам процесс представляет собой случайное блуждание системы S по состояниям. После первого шага система может оказаться в одном (и только в одном) из своих возможных состояний S1 (1), S2 (1), S3 (1); на втором шаге – S1 (2), S2 (2), S3 (2); на k шаге S1 (k), S2 (k), S3 (k).
Это последовательность («цепь») событий подлежит нашему изучению. Наиболее важной ее характеристикой являются вероятности состояний системы
P {S(k) = si} (i = 1,2,…,n; k=0,1,2,….),
где P {S(k) = si} – вероятность того, что на k-м шаге система S будет находиться в состоянии si.
Распределение вероятностей представляет собой одномерный закон распределения случайного процесса S (t), протекающего в системе.
Основной задачей исследования марковских цепей является нахождение безусловных вероятностей нахождения системы S на любом (k-ом) шаге в состоянии si ; обозначим эту вероятность pi (k).
Для нахождения этих вероятностей необходимо знать условные вероятности перехода системы S на k-м шаге в состояние sj, если известно, что на предыдущем (k-1)-м шаге она была в состоянии si.Обозначим эту вероятность
pij = P{S(k) = si| S (k-1) = si} (i = 1,2,…,n).
Вероятности pij(k) называются переходными вероятностями марковской цепи на k-м шаге. Вероятность Pii(k) есть вероятность того, что на k-м шаге система придет в то же состояния (задержится/останется) в состоянии si.
Переходные вероятности записаны в виде квадратной матрицы, размерностью, равной количеству изучаемых исходов, где элементами являются вектора вероятностей перехода доходности в индустриальной сети с одного состояния на другое.
P = 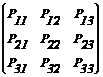 (1)
(1)
По диагонали матрицы стоят вероятности задержки системы в этом же данном состоянии.
На каждом шаге система может находиться только в одном из взаимно исключающих состояний, и сумма вероятностей в строке матрицы равна 1.
Чтобы найти безусловные вероятности Pi (k), недостаточно знать матрицу переходных вероятностей (1); нужно еще знать начальное распределение вероятностей, т. е. вероятности состояний рi(0), соответствующие началу процесса – моменту t0 .
Теперь зная начальное распределение вероятностей pi(0) и матрицу переходных вероятностей, мы можем найти безусловную вероятность нахождения системы на k-ом шаге в состоянии sj .
![]()
Представим модель в виде ориентированного взвешенного графа переходов (рис.2).
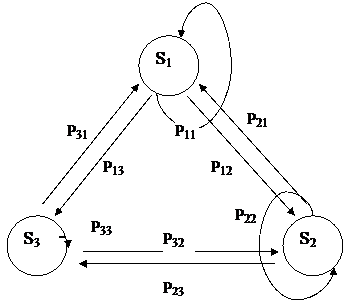
Рис.2. Граф переходов
Вершины графа обозначают состояние системы, а стрелки указывают направления возможных переходов из состояния в состояние. Возле каждой стрелки указывается соответствующая вероятность перехода.
Эти состояния имеют существенное значение, т.к. с их помощью можно прогнозировать будущие состояния системы для краткосрочной или долгосрочной перспективы.
Описанный процесс можно превратить в управляемый процесс, предположив дополнительно, что в каждый момент времени tk = k, k=1,2,…N, мы можем вмешаться в ход процесса, оказав на него конкретное воздействие из заданного множества воздействий A= {a1, a2, ….ak}. При этом переходные вероятности будут зависеть от соответствующего воздействия или управления ![]() .
.
Пусть, Sj, j=1,…m – возможные состояние системы в момент времени tk = k, k=1,2,…N, A= {a1, a2, ….ak} – множество возможных решений ЛПР, P1, P2, ……..Pk – матрицы одношаговых переходных вероятностей, Pk = ![]() , соответствующих выбору одного определенного решения аk из А, а Rk=
, соответствующих выбору одного определенного решения аk из А, а Rk=![]() - матрица доходов. Элементы матрицы Rk можно интерпретировать следующим образом:
- матрица доходов. Элементы матрицы Rk можно интерпретировать следующим образом: ![]() - это величина дохода при выборе стратегии
- это величина дохода при выборе стратегии ![]() , связанная с одношаговым переходом системы из состояния Si в состояние Sj с вероятностью
, связанная с одношаговым переходом системы из состояния Si в состояние Sj с вероятностью ![]() для всех i,j =1,…m.
для всех i,j =1,…m.
Рассмотрим функционирование управляемого процесса в два соседних момента времени t и t+1, как показано на рисунке 3.

Рис. 3. Временная диаграмма с состояниями {Si} и функциями средних оптимальных доходов Ft(i), i=1,….m.
Введем в рассмотрение последовательность функций оптимального поведения {ft(i)} и определим каждую ft(i) как функцию оптимального дохода на этапах после момента времени t, ![]() , при условии, что процесс находится в заданном состоянии Si, а в следующий момент она переходит в состояние Sj при выборе управления
, при условии, что процесс находится в заданном состоянии Si, а в следующий момент она переходит в состояние Sj при выборе управления ![]() , то суммарная величина дохода будет равна:
, то суммарная величина дохода будет равна:
![]() i,j =1,…m, (2)
i,j =1,…m, (2)
где ft+1(j) – оптимальная величина усредненного по вероятностям суммарного дохода на этапах после момента t+1.
Величина (2) имеет вероятность ![]() , следовательно, средняя величина дохода, которая соответствует выбору
, следовательно, средняя величина дохода, которая соответствует выбору ![]() в момент времени t, будет равна
в момент времени t, будет равна
![]() (3)
(3)
Если система находилась в момент времени t в состоянии Si, эта величина зависит от выбранного в момент времени t решения ![]() . Если максимизировать ее по всем
. Если максимизировать ее по всем ![]() и обозначив результат через ft(i), получим функциональное уравнение для Марковского процесса:
и обозначив результат через ft(i), получим функциональное уравнение для Марковского процесса:
![]() (4)
(4)
для всех состояний Si, i=1,….m, и моментов времени t, t=N, N-1,……1.
Функции ft(i), i=1,……..m, как максимальный уровень дохода для всего горизонта планирования, состоящего из N этапов, будут характеризовать конкретное состояние Si, i=1,….m.
Движущей силой объединения хозяйствующих субъектов является возможность получения каждым из участников дополнительной выгоды от него. Дополнительная выгода может выражаться в стабилизации финансово-хозяйственного положения, повышении объема производства, снижении затрат на НИОКР; повышении квалификации сотрудников, решении социально-экологических проблем, повышении эффективности использования ресурсов, т.е. в получении дополнительного дохода.
Заключение
Итак, в данной работе предпринята попытка показать, каким образом стохастический подход может быть использован для анализа доходности индустриальных сетей - сложных сетевых структур, действующих на современных рынках. Для индустриальных сетей характерны такие признаки как: открытость – для материальных потоков, информации; нелинейность – множество путей эволюции системы и возможность выбора из данных альтернатив; когерентность (сцепление, связь) – согласованное протекание во времени процессов в данной системе; хаотический характер переходных состояний в них; непредсказуемость их поведения; способность активно взаимодействовать со средой, изменять ее в направлении, обеспечивающем наиболее успешное функционирование системы; способность учитывать прошлый опыт; гибкость структуры. Получение дохода в индустриальных сетях является своего рода ориентиром, позволяющим руководителям сотрудничающих предприятий принимать решения о дальнейшем прекращении или же о продолжении взаимодействия. Дальнейшим развитием представленной работы, показавшей, как можно смоделировать процесс управления доходностью в индустриальных сетях с помощью Марковских процессов, может быть исследование вопросов распределения доходов между участниками сети.
Литература
1. В. Вайдлих. Социодинамика: системный подход к математическому моделированию в социальных науках - М.: УРСС. – 2003, - 480 c.
2. Ветрова Н.А., Горлачева Е.Н., Гудков А.Г. Анализ и моделирование технологических инноваций // Известия ВУЗов. Машиностроение. – 2005. – ╧11. – С.47– 58.
3. Горлачева Е.Н. Стратегические альянсы как форма межфирменного взаимодействия // Машиностроитель. – 2008.- ╧7.- С.6-12.
4. Горлачева Е.Н. Механизм межфирменного взаимодействия // Инженер. Технолог. Рабочий. – 2008. – ╧4. – С.2–8.
5. Горлачева Е.Н., Омельченко И.Н. Роль межфирменного взаимодействия при реализации концепции открытых инноваций // Наука и образование: электронное научно-техническое издание. – 2010. - ╧12. – С.1-17. // http://technomag.edu.ru/doc/163089.html
6. Петров А.А., Поспелов И.Г., Шананин А.А. Опыт математического моделирования экономики. - М.: Энергоатомиздат, 1996. - 544 с.
7. Проектирование интегрированных производственно-корпоративных структур: эффективность, организация, управление / под ред. А.А. Колобова, А.И. Орлова. – М.: Из-во МГТУ им. Н.Э. Баумана, 2006. – 728 с.
8. Саркисян Р.Е. Системный анализ и принятие решений. Вероятностные модели и методы. – М.: МИИТ, 2009 – 255 с. – Ч.3.
9. Соловьев В.И. Стохастические модели математической экономики и финансовой экономики. Уч. Пос. -М.: ГУУ, 2001. – 92 с.
10. Третьяк. О.А. Маркетинг: новые ориентиры модели управления. – М.: ИНФРА-М, 2005. – 405 с.
11. Шерешева М. Ю. Формы сетевого взаимодействия компаний. – М.: ГУ-ВШЭ, 2010. – 291 с.
12. Шерешева М.Ю. Типы сетевого межфирменного взаимодействия // Развитие форм межфирменной кооперации: сети и взаимоотношения: Доклады участников Сети мастерства. М.:ИД ГУ-ВШЭ, 2008. С.24-59.
13. Grandori A., Soda G. Inter-Firm Networks: Antecedents, Mechanisms and Forms // Organization Studies. – 1995. – Vol.16. – ╧ 2.
14. Hamel G., Prahalad C.K. Competing for the future – Harvard: Harvard Business Review, 1996 – 384 p.
15. Miles R.F., Snow C.C. Network Organizations: New Concepts for New Forms // California Management Review. – 1986. – Vol.28. – N. 3.
16. Möller K., Rajala A. Rise of Strategic Nets — New Modes of Value Creation // Industrial Marketing Management. – 2007. – Vol.36. – ╧ 7.
17. Prasad R. Emerging Paradigm of Strategic R&D alliances vis-à-vis corporate international competitiveness // Technology Experts. 2004. – Vol.VII-╧1. – P.1-6.
18. Riemer K., Gogolin M., Klein S. Introduction to Organizational Networks: Emergence, Motives, Classification and Types. Teaching Note. – Institut fuer Wirtschaftsinformatik, Universitaet Muenster, 2005.
19. G. Silverberg, B. Verspagen Self-organization of R&D search in complex technology spaces // Journal of economic interaction and coordination. – 2007. - ╧2. – 195-210.
20. Storgeon T.J. Modular production networks: a new American model of industrial organization // Industrial and Corporate Change. 2002. Vol.11. ╧3
Публикации с ключевыми словами: стохастический подход, индустриальные сети, межфирменное взаимодействие
Публикации со словами: стохастический подход, индустриальные сети, межфирменное взаимодействие
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



