научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 09, сентябрь 2010
DOI: 10.7463/0910.0157379
УДК 519.6
МГТУ им. Н.Э. Баумана,
apkarpenko@mail.ru
Введение
Корпоративная база знаний представляет собой, как правило, совокупность разного рода слабоструктурированных документов, в которых с той или иной степенью подробности описаны прецеденты – ситуации и решения, которые были приняты в этих ситуациях. В системах поддержки принятия решений (СППР), которые используют такие базы знаний, поиск решения заключается в поиске в этих базах наиболее подходящих прецедентов и соответствующих им документов [1]. В работе рассматривается поиск решений по атрибутам документов, содержащимся в их метаданных, как альтернатива полнотекстовому поиску.
Классический атрибутивный поиск основывается на использовании в качестве метаданных документа преимущественно его регистрационных атрибутов [2]. В работе рассматривается иной подход к поиску решений в базах знаний прецедентов, когда метаданные формируются на основе онтологии соответствующей предметной области, заданной в виде семантической сети. При этом релевантность документа оценивается близостью в некоторой метрике семантической сети этого документа и семантической сети запроса.
В работе существенно используется «важность» концептов в семантической сети рассматриваемой онтологической базы знаний. Ряд мер этой важности предложен в нашей работе [3].
Важной составной частью предлагаемой методики оценки релевантности документа является построение семантической сети этого документа. В работе данная задача ставится, как задача огрубления графа семантической сети онтологии рассматриваемой предметной области [4,5]. Рассматриваются три метода решения задачи на основе насыщенных паросочетаний – методы, использующие случайные паросочетания, паросочетания из тяжелых ребер, а также паросочетания из тяжелых клик [4, 6,7].
В общей постановке о задаче поиска информации следует говорить в терминах модели поиска, которая включает в себя способ представления документов, способ представления поисковых запросов, вид критерия релевантности документов [8].
В данной работе документы в базе знаний, а также поисковые запросы к базе представляются в виде фреймов, которые называются паттерном проектирования и паттерном запроса соответсвенно. Слоты этих паттернов соответствуют ролям концептов используемой онтологии (предметная область, объект, свойство, действие, задача и т.д.) [1].
Указанные роли разбивают концепты онтологии, документа и запроса к базе знаний на кластеры. Предполагается, что по методике построения семантической сети документа, построены семантические сети указанных кластеров. Таким образом, поисковые образы документа и запроса представляются в виде совокупности семантических сетей, соответствующих слотам паттерна проектирования и паттерна запроса.
В работе предложено несколько мер релевантности ролевых кластеров документа, формализующих близость семантических сетей поискового образа документа и семантических сетей запроса. На основе указанных мер предложен алгоритм оценки релевантности документа запросу.
1. Построение семантической сети документа
Представим семантическую сеть ![]() рассматриваемой онтологии
рассматриваемой онтологии ![]() в виде взвешенного связного мультиграфа
в виде взвешенного связного мультиграфа ![]() . Узлы этого графа соответствуют концептам множества
. Узлы этого графа соответствуют концептам множества ![]() , а ребра – четким бинарным отношениям между ними, каждое из которых принадлежит одному из типов
, а ребра – четким бинарным отношениям между ними, каждое из которых принадлежит одному из типов ![]() .
.
Определены веса ![]() ,
, ![]() узлов графа
узлов графа ![]() , формализующие «важность» соответствующих концептов в сети
, формализующие «важность» соответствующих концептов в сети ![]() . Для каждого из ребер
. Для каждого из ребер ![]() ,
, ![]()
![]() графа
графа ![]() полагается заданным также
полагается заданным также ![]() -вектор весов
-вектор весов ![]() , где
, где ![]() , если концепты
, если концепты ![]() не связаны между собой отношением типа
не связаны между собой отношением типа ![]() , и
, и ![]() - в противном случае. Здесь
- в противном случае. Здесь ![]() - априори заданный вес отношений типа
- априори заданный вес отношений типа ![]() в онтологии
в онтологии ![]() .
.
Некоторые методы определения весов концептов ![]() и весов отношений
и весов отношений ![]() предложены в работе [3]. Для определения весов концептов может быть также использована их семантическая близость, полученная с помощью соответствующего словаря [9] или Википедии [10]. Веса концептов могут быть сформированы также на основе понятий центральности по близости и центральности по посредничеству [11].
предложены в работе [3]. Для определения весов концептов может быть также использована их семантическая близость, полученная с помощью соответствующего словаря [9] или Википедии [10]. Веса концептов могут быть сформированы также на основе понятий центральности по близости и центральности по посредничеству [11].
Перейдем, например, с помощью аддитивной свертки
![]() ,
, ![]() (1)
(1)
от взвешенного мультиграфа ![]() к взвешенному обыкновенному графу, в котором вес ребра
к взвешенному обыкновенному графу, в котором вес ребра ![]() равен
равен ![]() . Сохраним за полученным графом прежнее обозначение. Здесь и далее
. Сохраним за полученным графом прежнее обозначение. Здесь и далее ![]() ,
, ![]() - положительный скалярный вещественный множитель, определяющий относительный вес компонентов аддитивной скалярной свертки вида (1).
- положительный скалярный вещественный множитель, определяющий относительный вес компонентов аддитивной скалярной свертки вида (1).
Аналогично определим семантическую сеть ![]() документа
документа ![]() в виде связного взвешенного обыкновенного графа
в виде связного взвешенного обыкновенного графа ![]() . Узлы этого графа соответствуют
. Узлы этого графа соответствуют ![]() концептам
концептам ![]() документа
документа ![]() , а ребра – связям между ними. Вес узла графа
, а ребра – связям между ними. Вес узла графа ![]() , соответствующего концепту
, соответствующего концепту ![]() , обозначим
, обозначим ![]() , а атрибуты его ребра
, а атрибуты его ребра ![]() зададим парой
зададим парой ![]() , где
, где ![]() - «расстояние» между узлами
- «расстояние» между узлами ![]() , а
, а ![]() - вес ребра
- вес ребра ![]() .
.
В терминах графа ![]() задача построения семантической сети документа
задача построения семантической сети документа ![]() сводится к решению двух следующих задач.
сводится к решению двух следующих задач.
Задача 1 (задача определения топологии графа ![]() ) - по каким правилам связывать узлы этого графа ребрами, т.е. устанавливать связи между концептами множества
) - по каким правилам связывать узлы этого графа ребрами, т.е. устанавливать связи между концептами множества ![]() ?
?
Задача 2 (задача определения весов узлов и атрибуты ребер графа ![]() ) - исходя из каких соображений, назначать веса
) - исходя из каких соображений, назначать веса ![]() узлов этого графа, а также атрибуты
узлов этого графа, а также атрибуты ![]() ,
, ![]() его ребер?
его ребер?
1.1. Определение топологии графа ![]() . В общей постанове эту задачу следует отнести к задаче огрубления графа [4].
. В общей постанове эту задачу следует отнести к задаче огрубления графа [4].
Классические методы решения задачи огрубления графа основаны на итерационном стягивании смежных узлов графа ![]() в узлы графа
в узлы графа ![]() , где
, где ![]() - номер итерации,
- номер итерации, ![]() . В результате этого процесса ребро между двумя вершинами графа
. В результате этого процесса ребро между двумя вершинами графа ![]() удаляется и создается мультиузел графа
удаляется и создается мультиузел графа ![]() , объединяющий оба стягиваемых узла. Задача огрубления графа
, объединяющий оба стягиваемых узла. Задача огрубления графа ![]() до графа
до графа ![]() имеет ту специфику, что ни на одной из итераций указанного итерационного процесса в один узел не могут быть стянуты те узлы графа
имеет ту специфику, что ни на одной из итераций указанного итерационного процесса в один узел не могут быть стянуты те узлы графа ![]() , которые принадлежат графу
, которые принадлежат графу ![]() .
.
Обычно задача огрубления графа решается в терминах паросочетаний. Паросочетанием в графе называется набор его ребер, в котором любые два ребра не инцидентны общему узлу. Таким образом, граф ![]() строится на основе графа
строится на основе графа ![]() путем нахождения в графе
путем нахождения в графе ![]() паросочетания и стягивания в мультиузел узлов, входящих в каждую из пар этого паросочетания. Непарные узлы графа
паросочетания и стягивания в мультиузел узлов, входящих в каждую из пар этого паросочетания. Непарные узлы графа ![]() просто копируются в граф
просто копируются в граф ![]() . Важно, что граф, огрубленный с использованием паросочетаний, сохраняет многие свойства исходного графа. Так, например, если граф
. Важно, что граф, огрубленный с использованием паросочетаний, сохраняет многие свойства исходного графа. Так, например, если граф ![]() является планарным, то граф
является планарным, то граф ![]() также планарен [12].
также планарен [12].
В терминах паросочетаний специфика нашего случая состоит в том, что любая пара узлов каждого из паросочетаний не может включать в себя одновременно два узла графа ![]() .
.
С точки зрения повышения эффективности процесса огрубления графа, целесообразно использовать насыщенные паросочетания - паросочетания в которых хотя бы один узел любого ребра, не вошедшего в паросочетание, инцидентен ребру, вошедшему в паросочетание. Вообще говоря, с той же точки желательным является использование максимальных паросочетаний - насыщенных паросочетаний, которые имеют максимальное число ребер. Однако, вычислительная сложность формирования максимальных паросочетаний, в общем случае, значительно выше аналогичной вычислительной сложности для просто насыщенных паросочетаний. Поэтому обычно в вычислительной практике ограничиваются последними [7].
Утверждение 1. Оценка снизу количества итераций, необходимых для построения графа ![]() с использованием насыщенных паросочетаний равна
с использованием насыщенных паросочетаний равна ![]() .
.
Справедливость утверждения следует из того факта, что при использовании насыщенных паросочетаний число узлов графа ![]() не может быть, очевидно, меньше половины числа узлов графа
не может быть, очевидно, меньше половины числа узлов графа ![]() .
.
Наиболее известны три следующих метода построения насыщенных паросочетаний: случайное паросочетание (RM); паросочетание из тяжелых ребер (HEM); паросочетание из тяжелых клик (HCM) [5].
Случайное паросочетание на итерации ![]() строится по следующей схеме:
строится по следующей схеме:
1) все узлы ![]() текущего графа
текущего графа ![]() объявляем немаркированными;
объявляем немаркированными;
2) случайным образом выбираем немаркированный узел, еще не включенный в паросочетание - пусть это будет узле ![]() ;
;
3) из числа немаркированных узлов, смежных узлу ![]() , случайным образом выбираем узел (пусть это будет узел
, случайным образом выбираем узел (пусть это будет узел ![]() ), также еще не включенный в паросочетание;
), также еще не включенный в паросочетание;
4) если оба узла или один из узлов пары ![]() не принадлежат графу
не принадлежат графу ![]() , то включаем ребро
, то включаем ребро ![]() в паросочетание, и узлы
в паросочетание, и узлы ![]() маркируем;
маркируем;
5) если ни одного немаркированного узла, смежного узлу ![]() , не существует, то узел
, не существует, то узел ![]() маркируем и оставляем свободным (чтобы затем перенести его в граф
маркируем и оставляем свободным (чтобы затем перенести его в граф ![]() );
);
6) если в графе ![]() имеются еще немаркированные узлы, то переходим к шагу 2.
имеются еще немаркированные узлы, то переходим к шагу 2.
Данную схему иллюстрирует рисунок 1, на котором слева показан граф ![]() и сформированное на его основе паросочетание, а справа – граф
и сформированное на его основе паросочетание, а справа – граф ![]() .
.
Паросочетание из тяжелых ребер. Схема построения этого паросочетания отличается от рассмотренной выше схемы шагом 3, который в данном случае формулируется следующим образом. Из числа немаркированных узлов, смежных узлу ![]() , выбираем такой узел
, выбираем такой узел ![]() , еще не включенный в паросочетание, что вес ребра
, еще не включенный в паросочетание, что вес ребра ![]() является максимальным среди весов всех возможных ребер, связанных с узлом
является максимальным среди весов всех возможных ребер, связанных с узлом ![]() .
.

Рисунок 1 – К методу случайных паросочетаний: квадратиками показаны узлы графа ![]() : а) граф
: а) граф ![]() ; б) граф
; б) граф ![]()
Паросочетание из тяжелых клик. В данном случае также меняется только шаг 3 рассмотренной схемы формирования случайного паросочетания: из числа немаркированных узлов, смежных узлу ![]() , выбираем такой узел
, выбираем такой узел ![]() , еще не включенный в паросочетание, что реберная плотность мультиузла, который получается стягиванием узлов
, еще не включенный в паросочетание, что реберная плотность мультиузла, который получается стягиванием узлов ![]() , является максимально возможной по сравнению со всеми иными вариантами выбора узла
, является максимально возможной по сравнению со всеми иными вариантами выбора узла ![]() .
.
Итерации во всех рассмотренных методах формирования паросочетания заканчиваются, когда в результате данной итерации не удалось выделить ни одной пары узлов. Другими словами, итерации заканчиваются, если в текущем графе ![]() содержатся только узлы графа
содержатся только узлы графа ![]() .
.
Отметим следующее обстоятельство. В силу наличия элемента случайности при формировании паросочетаний, различные итерационные процессы порождают, вообще говоря, графы ![]() , имеющие различную топологию. Таким образом, возникает задача получения в некотором смысле наилучшего графа
, имеющие различную топологию. Таким образом, возникает задача получения в некотором смысле наилучшего графа ![]() . При этом в качестве максимизируемого критерия оптимальности графа можно использовать, например, его реберную плотность (коэффициент кластеризации) [3,11].
. При этом в качестве максимизируемого критерия оптимальности графа можно использовать, например, его реберную плотность (коэффициент кластеризации) [3,11].
1.2. Определение весов узлов и ребер графа ![]() . Выделим два случая:
. Выделим два случая:
1) рассматриваемая пара узлов паросочетания включает в себя узел, принадлежащий графу ![]() (например, пара
(например, пара ![]() на рисунке 1);
на рисунке 1);
2) пара узлов содержит только узлы, не принадлежащие графу ![]() (например, пара
(например, пара ![]() на том же рисунке).
на том же рисунке).
Случай 1. Пусть рассматриваемая пара включает в себя узел (или мультиузел) ![]() и узел (или мультиузел)
и узел (или мультиузел) ![]() , веса которых равны
, веса которых равны ![]() ,
, ![]() соответственно, а атрибуты ребра
соответственно, а атрибуты ребра ![]() ,
, ![]() определяется парой
определяется парой ![]() . Отметим, что во веденных обозначениях надиндекс
. Отметим, что во веденных обозначениях надиндекс ![]() указывает на то, что в процессе огрубления графа
указывает на то, что в процессе огрубления графа ![]() веса его узлов и ребер, вообще говоря, изменяются. Здесь и далее в данном разделе для простоты записи индекс
веса его узлов и ребер, вообще говоря, изменяются. Здесь и далее в данном разделе для простоты записи индекс ![]() в обозначениях опущен.
в обозначениях опущен.
Будем полагать, что в процессе стягивания узлов ![]() ,
, ![]() узел
узел ![]() стягивается к
стягивается к ![]() , так что в результате получается мультиузел
, так что в результате получается мультиузел ![]() , вес которого равен
, вес которого равен ![]() . Условно результат данной процедуры будем записывать в виде
. Условно результат данной процедуры будем записывать в виде ![]() .
.
Логично исходить из того, что вес ![]() является некоторой положительной возрастающей функций своих аргументов
является некоторой положительной возрастающей функций своих аргументов ![]() ,
, ![]() ,
, ![]() и такой же убывающей функций аргумента
и такой же убывающей функций аргумента ![]() . В простейшем случае в качестве такой функции может быть использована функция вида
. В простейшем случае в качестве такой функции может быть использована функция вида
 . (2)
. (2)
В результате стягивания узла ![]() к узлу
к узлу ![]() атрибуты ребер, инцидентных узлу
атрибуты ребер, инцидентных узлу ![]() , не меняются, а значения атрибутов ребер, инцидентных узлу
, не меняются, а значения атрибутов ребер, инцидентных узлу ![]() , должны быть по некоторому правилу изменены. Рассмотрим одно из таких ребер
, должны быть по некоторому правилу изменены. Рассмотрим одно из таких ребер ![]() , атрибуты которого равны
, атрибуты которого равны ![]() . Это ребро заменяется на ребро
. Это ребро заменяется на ребро ![]() , которому соответствуют атрибуты
, которому соответствуют атрибуты ![]() .
.
Естественно положить, что длина ребра ![]() равна
равна
![]() ,
,
т.е. на длину ребра ![]() превышает длину ребра
превышает длину ребра ![]() . Логично также принять, что вес ребра
. Логично также принять, что вес ребра ![]() является некоторой положительной возрастающей функцией своих аргументов. В простейшем случае можно положить
является некоторой положительной возрастающей функцией своих аргументов. В простейшем случае можно положить
![]() . (3)
. (3)
Схему рассмотренного алгоритма иллюстрирует рисунок 2. Здесь принято, что
 , (4)
, (4)
![]() . (5)
. (5)
Случай 2. Положим, что оба узла рассматриваемой пары ![]() не принадлежат графу
не принадлежат графу ![]() , т.е. когда имеет место ситуация
, т.е. когда имеет место ситуация ![]() . Как и ранее, положим, что веса указанных узлов равны
. Как и ранее, положим, что веса указанных узлов равны ![]() ,
, ![]() , а атрибуты ребра
, а атрибуты ребра ![]() ,
, ![]() определяется парой
определяется парой ![]() .
.
В этом случае также можно считать, что один из узлов (пусть это будет узел ![]() ) стягивается к другому узлу (
) стягивается к другому узлу (![]() ), так что в результате получается мультиузел
), так что в результате получается мультиузел ![]() ,
, ![]() Как и в предыдущем случае, положим, что вес этого узла равен
Как и в предыдущем случае, положим, что вес этого узла равен ![]() и представляет собой, например, функцию вида (2).
и представляет собой, например, функцию вида (2).

Рисунок 2 – К стягиванию узла (мультиузла) ![]() и узла (мультиузла)
и узла (мультиузла) ![]() : квадратиками показаны узлы графа
: квадратиками показаны узлы графа ![]()
В отличие от предыдущего случая, здесь логично положить, что в результате стягивания узла ![]() к узлу
к узлу ![]() меняются значения атрибутов всех ребер, инцидентных как узлу
меняются значения атрибутов всех ребер, инцидентных как узлу ![]() , так и узлу
, так и узлу ![]() . Рассмотрим ребра
. Рассмотрим ребра ![]() ,
, ![]() , атрибуты которых равны
, атрибуты которых равны ![]() ,
, ![]() соответственно. Эти ребра заменяются на ребра
соответственно. Эти ребра заменяются на ребра ![]() ,
, ![]() , которым соответствуют атрибуты
, которым соответствуют атрибуты ![]() ,
, ![]() , где
, где
![]() ,
, ![]() , (6)
, (6)
а веса ![]() ,
, ![]() определяются, например, по формуле вида (2).
определяются, например, по формуле вида (2).
Отметим, что принятые соглашения могут приводить к нецелым значениям расстояний между узлами графа ![]() , даже если все расстояния между узлами графа
, даже если все расстояния между узлами графа ![]() являются целыми.
являются целыми.
Схему рассмотренного алгоритма иллюстрирует рисунок 3. Здесь принято, что вес узла ![]() определяется по формуле (4), веса ребер графа
определяется по формуле (4), веса ребер графа ![]() - по формуле (5), а расстояние между узлами этого графа – по формуле (6).
- по формуле (5), а расстояние между узлами этого графа – по формуле (6).

Рисунок 3 – К стягиванию узлов (мультиузлов) ![]()
В результате итерации ![]() в графе
в графе ![]() могут появиться кратные ребра (см., например, узлы
могут появиться кратные ребра (см., например, узлы ![]() ,
, ![]() на рисунке 1а). Прежде чем переходить к основному циклу итерации
на рисунке 1а). Прежде чем переходить к основному циклу итерации ![]() эти ребра следует объединить. Возникает вопрос, как вычислить значения атрибутов полученного ребра?
эти ребра следует объединить. Возникает вопрос, как вычислить значения атрибутов полученного ребра?
Положим, что двумя ребрами связаны узлы ![]() ,
, ![]() , и атрибуты этих ребер равны
, и атрибуты этих ребер равны ![]() ,
, ![]() . В качестве расстояния между этими узлами
. В качестве расстояния между этими узлами ![]() примем минимальное из расстояний
примем минимальное из расстояний ![]() ,
, ![]() :
:
![]() .
.
В качестве веса ![]() логично принять сумму весов указанных ребер:
логично принять сумму весов указанных ребер:
![]() .
.
Таким образом, после завершения итераций оказываются полностью определенными топология графа ![]() , а также веса его узлов
, а также веса его узлов ![]() и значения атрибутов его ребер
и значения атрибутов его ребер ![]() ;
; ![]() ,
, ![]() .
.
Вернемся к использованию в обозначениях весов узлов и атрибутов ребер графа ![]() индекса
индекса ![]() .
.
Исключим из числа атрибутов ребер графа ![]() расстояния
расстояния ![]() и модифицируем веса
и модифицируем веса ![]() ребер этого графа: положим, что «новый» вес ребра
ребер этого графа: положим, что «новый» вес ребра ![]() равен
равен ![]() , где
, где ![]() - некоторая положительная убывающая функция расстояния
- некоторая положительная убывающая функция расстояния ![]() и такая же возрастающая функция «старого» веса
и такая же возрастающая функция «старого» веса ![]() . Например, можно принять
. Например, можно принять
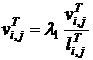 . (7)
. (7)
При необходимости, можно нормировать веса узлов и ребер полученного графа ![]() , например, следующим образом:
, например, следующим образом:
 ;
; 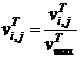 ;
; ![]() ;
; ![]() .
.
Здесь ![]() ,
, ![]() - максимальный вес узла и ребра в графе
- максимальный вес узла и ребра в графе ![]() соответственно.
соответственно.
2. Ролевая кластеризация семантических сетей онтологии и документа
Положим, что выделено ![]() ролей
ролей ![]() ,
, ![]() концептов. Роли
концептов. Роли ![]() разбивают все множество концептов
разбивают все множество концептов ![]() на
на ![]() непересекающихся «ролевых» кластеров
непересекающихся «ролевых» кластеров ![]() , среди которых могут быть и пустые кластеры. Множество концептов, принадлежащих кластеру
, среди которых могут быть и пустые кластеры. Множество концептов, принадлежащих кластеру ![]() , обозначим
, обозначим ![]() , так что
, так что
 .
.
Число концептов в кластере ![]() (или, что то же самое, во множестве
(или, что то же самое, во множестве ![]() ) обозначим
) обозначим ![]() . Очевидно, что
. Очевидно, что
 .
.
Аналогично, роли ![]() разбивают множество концептов
разбивают множество концептов ![]() документа
документа ![]() на
на ![]() ролевых кластеров
ролевых кластеров ![]() , концепты которых образуют множества
, концепты которых образуют множества ![]() с числом концептов в них, равным
с числом концептов в них, равным ![]() :
:
 ;
; 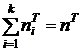 .
.
Кластерам ![]() ,
, ![]() поставим в соответствие их семантические сети
поставим в соответствие их семантические сети ![]() ,
, ![]() и графы
и графы ![]() ,
, ![]() ;
; ![]() . Обозначим
. Обозначим ![]() - вес узла
- вес узла ![]() графа
графа ![]() ,
, ![]() - вес ребра графа
- вес ребра графа ![]() , связывающего его узлы
, связывающего его узлы ![]() . Здесь
. Здесь ![]() ,
,![]() . Аналогичные обозначения
. Аналогичные обозначения ![]() ,
, ![]() введем для графа
введем для графа ![]() .
.
Графы ![]() ,
, ![]() ,
, ![]() ролевых кластеров
ролевых кластеров ![]() ,
, ![]() могут быть построены по схеме, рассмотренной в п.1. При этом графы
могут быть построены по схеме, рассмотренной в п.1. При этом графы ![]() строятся на основе графа
строятся на основе графа ![]() , а графы
, а графы ![]() - на основе графа
- на основе графа ![]() .
.
Отметим, что оценить качество рассмотренной ролевой кластеризации можно, например, с помощью величины, которая называется модулярность (modularity) графа [13].
3. Поисковые образы документа и запроса
Пусть в семантической сети документа ![]() выделены ролевые кластеры
выделены ролевые кластеры ![]() и тем или иным образом построены семантические сети этих кластеров
и тем или иным образом построены семантические сети этих кластеров ![]() , а также соответствующие им графы
, а также соответствующие им графы ![]() ;
; ![]() . Положим, что паттерн проектирования
. Положим, что паттерн проектирования ![]() документа
документа ![]() имеет
имеет ![]() слотов
слотов ![]() и слот
и слот ![]() соответствует роли
соответствует роли ![]() .
.
Поисковый образ рассматриваемого документа ![]() будем представлять в виде
будем представлять в виде ![]() семантических сетей
семантических сетей ![]() , формализованных в виде графов
, формализованных в виде графов ![]() ;
; ![]() - рисунок 4.
- рисунок 4.

Рисунок 4 – Поисковый образ документа ![]()
Не ограничивая общности рассуждений, положим, что поисковый образ запроса ![]() формируется паттерном
формируется паттерном ![]() , который также имеет
, который также имеет ![]() слотов
слотов ![]() .
.
Введем следующие обозначения:
![]() - множество концептов запроса
- множество концептов запроса ![]() ;
;
![]() - число концептов во множестве
- число концептов во множестве ![]() ;
;
![]() - ролевые кластеры множества
- ролевые кластеры множества ![]() ,
, ![]() ;
;
![]() - множество концептов кластера
- множество концептов кластера ![]() ,
,
 ;
;
![]() - число концептов в кластере
- число концептов в кластере ![]() ,
,
 ;
;
![]() - семантическая сеть кластера
- семантическая сеть кластера ![]() ;
;
![]() - граф семантической сети
- граф семантической сети ![]() ;
;
![]() - вес узла
- вес узла ![]() графа
графа ![]() ;
;
![]() - вес ребра
- вес ребра ![]() графа
графа ![]() .
.
Здесь ![]() ,
, ![]() .
.
Таким образом, поисковый образ запроса ![]() представляет собой
представляет собой ![]() семантических сетей
семантических сетей ![]() , формализованных в виде графов
, формализованных в виде графов ![]() ;
; ![]() - рисунок 5.
- рисунок 5.
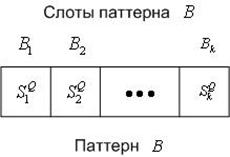
Рисунок 5 – Поисковый образ запроса ![]()
Графы ![]() ,
, ![]() ролевых кластеров
ролевых кластеров ![]() также могут быть построены по схеме, рассмотренной в п.1 на основе графа
также могут быть построены по схеме, рассмотренной в п.1 на основе графа ![]() .
.
4. Релевантность ролевого кластера документа
Можно предложить несколько мер релевантности ролевых кластеров документов, формализующих близость семантических сетей ![]() поискового образа документа
поискового образа документа ![]() и семантических сетей
и семантических сетей ![]() запроса
запроса ![]() или, что то же самое, мер близости соответствующих графов
или, что то же самое, мер близости соответствующих графов ![]() ,
, ![]() . Обозначим эти меры
. Обозначим эти меры ![]() .
.
Определим прежде меру близости концептов множества ![]()
![]() ,
,
где минимум берется по всем возможным цепям ![]() , в которых все концепты принадлежат множеству
, в которых все концепты принадлежат множеству ![]() .
.
Во множестве ![]() найдем для концепта
найдем для концепта ![]() , такого что
, такого что ![]() ,
, ![]() , концепт
, концепт ![]() , расстояние которого до концепта
, расстояние которого до концепта ![]() равно
равно ![]() . Включим полученный концепт
. Включим полученный концепт ![]() во множество
во множество ![]() . Повторим процедуру для всех концептов множества
. Повторим процедуру для всех концептов множества ![]() , которые не принадлежат множеству
, которые не принадлежат множеству ![]() . Полученный в результате кластер
. Полученный в результате кластер ![]() представляет собой совокупность концептов множества
представляет собой совокупность концептов множества ![]() , не принадлежащих множеству
, не принадлежащих множеству ![]() , но находящихся ближе всего (в смысле меры
, но находящихся ближе всего (в смысле меры ![]() ) к этому множеству. Положим, что мощность кластера
) к этому множеству. Положим, что мощность кластера ![]() равна
равна ![]() .
.
Аналогично, для каждого концепта ![]() , такого что
, такого что ![]() ,
, ![]() , найдем во множестве
, найдем во множестве ![]() концепт
концепт ![]() , расстояние которого до концепта
, расстояние которого до концепта ![]() равно
равно ![]() и включим все полученные концепты во множество
и включим все полученные концепты во множество ![]() . Кластер
. Кластер ![]() представляет собой совокупность концептов множества
представляет собой совокупность концептов множества ![]() , не принадлежащих множествам
, не принадлежащих множествам ![]() ,
, ![]() , но находящихся ближе всего (в смысле той же меры
, но находящихся ближе всего (в смысле той же меры ![]() ) к кластеру
) к кластеру ![]() . Мощность кластера
. Мощность кластера ![]() равна
равна ![]() . И.т.д.
. И.т.д.
Взаимосвязи кластеров ![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() ,
, ![]() иллюстрирует рисунок 6.
иллюстрирует рисунок 6.
Для каждого из концептов ![]() ,
, ![]() и концептов
и концептов ![]() определим функцию
определим функцию ![]() , которая является положительной возрастающей функцией относительно первого аргумента и такой же убывающей функцией относительно второго аргумента;
, которая является положительной возрастающей функцией относительно первого аргумента и такой же убывающей функцией относительно второго аргумента; ![]() Примером такой функции может служить функция
Примером такой функции может служить функция
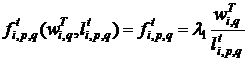 . (8)
. (8)
Функция ![]() формализует уменьшение весов концептов из кластеров
формализует уменьшение весов концептов из кластеров ![]() по мере «удаления» их от кластера
по мере «удаления» их от кластера ![]() .
.

Рисунок 6 – К взаимосвязям кластеров ![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() ,
, ![]()
4.1. Меры, не учитывающие веса концептов и связей между ними.
Мера на основе коэффициента Дайса, используемого при сравнении текстовых документов [14]
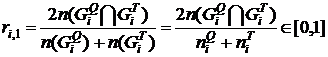 , (9)
, (9)
где ![]() ,
, ![]() - числа узлов графов
- числа узлов графов ![]() ,
, ![]() , соответственно;
, соответственно; ![]() - числа узлов, содержащихся как в графе
- числа узлов, содержащихся как в графе ![]() , так и в графе
, так и в графе ![]() .
.
Мера (9), по сути, представляет собой относительное число концептов кластера ![]() , содержащихся в кластере
, содержащихся в кластере ![]() , и в работе [14] называется мерой концептуальной близостью графов
, и в работе [14] называется мерой концептуальной близостью графов ![]() ,
, ![]() .
.
Здесь и далее полагается, что ![]() .
.
Мера на основе относительной близости графов ![]() ,
, ![]() [14]
[14]
 , (10)
, (10)
где ![]() ,
, ![]() - числа ребер, содержащихся в графах
- числа ребер, содержащихся в графах ![]() ,
, ![]() , соответственно;
, соответственно; ![]() - число ребер, содержащихся как в графе
- число ребер, содержащихся как в графе ![]() , так и в графе
, так и в графе ![]() .
.
Известно, что меры вида (9), (10) сильно зависят от размеров графов [14]. Поэтому целесообразно использовать их следующие модификации, учитывающие размеры графов ![]() ,
, ![]() .
.
Модифицированная мера на основе меры ![]()
 , (11)
, (11)
где
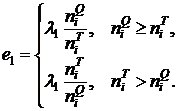 (12)
(12)
Модифицированная мера на основе меры ![]()
 , (13)
, (13)
где величина ![]() определяется по формуле вида (12).
определяется по формуле вида (12).
Очевидно, что при ![]() меры (12), (13) совпадают с мерами
меры (12), (13) совпадают с мерами ![]() ,
, ![]() соответственно, так что последние меры являются частным случаем мер (9), (10).
соответственно, так что последние меры являются частным случаем мер (9), (10).
Мера, являющаяся расширением меры ![]()
 . (14)
. (14)
Мера имеет смысл относительного числа узлов графа ![]() , содержащихся в графе
, содержащихся в графе ![]() , и графах
, и графах ![]() ,
, ![]() ,….
,….
Мера, являющаяся расширением меры ![]() и аналогичная мере (14)
и аналогичная мере (14)
 (15)
(15)
Здесь ![]() - число ребер, содержащихся в графе
- число ребер, содержащихся в графе ![]() ;
; ![]()
Отметим, что, очевидно, меры (14), (15) являются частными случаями мер (11), (13).
На основе мер (9) – (11), (13) – (15) легко сконструировать меры, которые учитывают только «сильные» узлы и ребра в графах ![]() ,
, ![]() ,
, ![]() ,…., т.е. узлы и ребра, веса которых превышают некоторые заданные величины [15].
,…., т.е. узлы и ребра, веса которых превышают некоторые заданные величины [15].
Аддитивная свертка мер ![]() ,
, ![]()
![]() , (16)
, (16)
включающая в себя все рассмотренные выше меры.
4.2. Меры, учитывающие веса концептов и связей между ними.
Взвешенная мера на основе меры ![]()
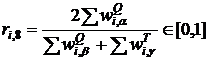 , (17)
, (17)
где индекс ![]() пробегает номера узлов, принадлежащих пересечению графов
пробегает номера узлов, принадлежащих пересечению графов ![]() , что условно будем записывать в виде
, что условно будем записывать в виде ![]() ; индексы
; индексы ![]() ,
, ![]() пробегают номера узлов
пробегают номера узлов ![]() ,
, ![]() соответственно.
соответственно.
Очевидно, что мера (17) эквивалентна мере (9), если принять следующие соглашения: ![]() при
при ![]() ;
; ![]() - в противном случае;
- в противном случае; ![]() ,
, ![]() . Таким образом, меру (9) можно считать частным случаем меры (17).
. Таким образом, меру (9) можно считать частным случаем меры (17).
Взвешенная мера на основе меры ![]()
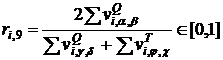 , (18)
, (18)
где, аналогично (17), ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() . Легко видеть, что мера (18) является частным случаем меры (10).
. Легко видеть, что мера (18) является частным случаем меры (10).
Модифицированная мера на основе меры ![]()
 . (19)
. (19)
Модифицированная мера на основе меры ![]()
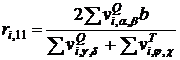 . (20)
. (20)
Мера, являющаяся расширением меры ![]()
 , (21)
, (21)
где ![]() ; индекс
; индекс ![]() пробегает номера узлов, принадлежащих графу
пробегает номера узлов, принадлежащих графу ![]() , что условно будем записывать в виде
, что условно будем записывать в виде ![]() ; аналогично
; аналогично ![]() .
.
Мера, являющаяся расширением меры ![]()
 , (22)
, (22)
аналогичная мере (21). Здесь ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() .
.
Аддитивная свертка мер ![]() ,
, ![]()
![]() , (23)
, (23)
включающая в себя все рассмотренные выше меры (17) – (22).
Модифицированная мера на основе меры ![]()
 , (24)
, (24)
где ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() .
.
Меры (17) – (24) также легко модифицировать, учитывая только «сильные» узлы и ребра в графах ![]() ,
, ![]() ,
, ![]() ,…. [15]. Значительное число мер релевантности ролевого кластера документа может быть построено на основе мер семантической близости в сетях документов [16].
,…. [15]. Значительное число мер релевантности ролевого кластера документа может быть построено на основе мер семантической близости в сетях документов [16].
5. Оценка релевантности документа
Пусть поисковый образ документа ![]() представлен паттерном проектирования
представлен паттерном проектирования ![]() , слотам которого
, слотам которого ![]() ,
, ![]() соответствуют семантические сети
соответствуют семантические сети ![]() , формализованные в виде графов
, формализованные в виде графов ![]() - рисунок 4. Пусть, аналогично, поисковый образ запроса
- рисунок 4. Пусть, аналогично, поисковый образ запроса ![]() сформирован в виде паттерна
сформирован в виде паттерна ![]() , который представляет собой совокупность
, который представляет собой совокупность ![]() семантических сетей
семантических сетей ![]() , формализованных в виде графов
, формализованных в виде графов ![]() - рисунок 5.
- рисунок 5.
Обозначим ![]() релевантность документа
релевантность документа ![]() запросу
запросу ![]() , где
, где ![]() - некоторая неотрицательная вещественно значная возрастающая функция всех своих аргументов, например,
- некоторая неотрицательная вещественно значная возрастающая функция всех своих аргументов, например,
 . (25)
. (25)
Нормировать величину ![]() можно, отнеся ее к сумме релевантностей всех рассматриваемых документов базы знаний.
можно, отнеся ее к сумме релевантностей всех рассматриваемых документов базы знаний.
Общая схема предлагаемой методики оценки релевантности документа ![]() имеет вид, представленный на рисунке 7.
имеет вид, представленный на рисунке 7.
Определение релевантности (25) можно расширить путем учета априорной «значимости» документа ![]() , которую можно построить, например, на основе мер
, которую можно построить, например, на основе мер ![]() близости семантических сетей
близости семантических сетей ![]() онтологии и семантических сетей
онтологии и семантических сетей ![]() документа
документа ![]() или, что то же самое, мер близости соответствующих графов
или, что то же самое, мер близости соответствующих графов ![]() ,
, ![]() ;
; ![]() . Так в качестве меры
. Так в качестве меры ![]() значимости документа
значимости документа ![]() можно использовать подходящим образом нормированную взвешенную сумму мер
можно использовать подходящим образом нормированную взвешенную сумму мер ![]() :
:
 . (26)
. (26)

Рисунок 7 - Схема оценки релевантности документа
С учетом меры ![]() формула (25) модифицируется следующим образом:
формула (25) модифицируется следующим образом:
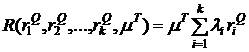 . (27)
. (27)
Отметим, что формулы (25), (27) не учитывают эффективность решений, которые содержатся в документе ![]() . На основе опыта эксплуатации рассматриваемой базы знаний эта эффективность может быть оценена лицом, принимающим решения и сохранена в базе знаний.
. На основе опыта эксплуатации рассматриваемой базы знаний эта эффективность может быть оценена лицом, принимающим решения и сохранена в базе знаний.
Заключение
Предложенная в работе методика оценки релевантности документов обладает высокой вычислительной сложностью. Подавляющая часть требуемых вычислительных затрат обусловлена выполнением следующих работ.
Во-первых, для каждого из документов ![]() базы знаний методика требует построения соответствующей семантической сети
базы знаний методика требует построения соответствующей семантической сети ![]() , а также построения семантической сети
, а также построения семантической сети ![]() ,
, ![]() каждого из слотов поискового образа документа (паттерна проектирования). Если онтология предметной области фиксирована, то эта работа выполняется лишь однажды, при помещении документа в базу знаний.
каждого из слотов поискового образа документа (паттерна проектирования). Если онтология предметной области фиксирована, то эта работа выполняется лишь однажды, при помещении документа в базу знаний.
Во-вторых, методика требует построения аналогичных семантических сетей ![]() онтологии рассматриваемой предметной области. Опять же, если онтология предметной области фиксирована, то эта работа выполняется лишь однократно.
онтологии рассматриваемой предметной области. Опять же, если онтология предметной области фиксирована, то эта работа выполняется лишь однократно.
В-третьих, в соответствии с методикой для каждого из запросов ![]() также требуется формирование семантических сетей
также требуется формирование семантических сетей ![]() . Данная работа должна выполняться системой управления базой знаний при обработке каждого из запросов.
. Данная работа должна выполняться системой управления базой знаний при обработке каждого из запросов.
В работе широко используется аддитивная скалярная свертка (см., например, формулы (1), (2), (3), (7) и т.д.). Очевидно, что наряду с аддитивными свертками могут быть использованы и иные, например, мультипликативные свертки или их комбинация [17].
Основная задача работы – задача определения релевантности документа – является, по сути, задачей многокритериальной (точнее - ![]() -критериальной) оптимизации – см. формулы (25), (27). Использованный при решении этой задачи метод аддитивной скалярной свертки является простейшим и далеко не всегда эффективным методом решения многокритериальных задач. Поэтому представляет интерес исследование целесообразности использования других, более «тонких» методов решения указанной многокритериальной задачи [17].
-критериальной) оптимизации – см. формулы (25), (27). Использованный при решении этой задачи метод аддитивной скалярной свертки является простейшим и далеко не всегда эффективным методом решения многокритериальных задач. Поэтому представляет интерес исследование целесообразности использования других, более «тонких» методов решения указанной многокритериальной задачи [17].
Широкое использование сверток приводит к тому, что методика содержит большое число свободных параметров (см. формулы (1), (2), (3), (7) и т.д.). Имеется немного содержательных оснований для априорного выбора значений этих параметров. Поэтому представляется перспективным ставить задачу определения их значений, как задачу метаоптимизации [18]. Отметим, что при этом в базе знаний требуется хранить оценки успешности поиска, сформированные лицом, принимающим решения.
Одной из проблем, которая возникает при использовании рассмотренного подхода к определению релевантности документов, является проблема лексической многозначности терминов. Правильное значение многозначного слова может быть установлено только путем анализа контекста, в котором это слово упоминается. Известен ряд методов решения данной задачи, например, методы, основанные на использовании Википедии [19].
В развитие работы планируется экспериментальная проверка эффективности предложенной методики.
Автор выражает благодарность И.П. Норенкову за постановку рассмотренной в работе задачи, а также за конструктивные обсуждения подходов к ее решению.
Работа выполнена при поддержке гранта РФФИ 10-07-00401.
Литература
1. И.П. Норенков. Интеллектуальные технологии на базе онтологий // Информационные технологии, 2010, ╧1, с.17-23.
2. The Dublin Core Metadata Initiative [Электронныйресурс]. (http://dublincore.org/).
3. А.П. Карпенко. Меры важности концептов в семантической сети онтологической базы знаний [Электронный ресурс] // Наука и образование: электронное научно- техническое издание, 2010, 7. (http://technomag.edu.ru/doc/151142.html).
4. G. Karypis, V. Kumar. Multilevel k-way Partitioning Scheme for Irregular Graphs // Journal of Parallel and Distributed Computing, 1998, vol. 8, no. 1, pp. 96-129.
5. Д.П. Бувайло, В.А. Толок. Быстрый высокопроизводительный алгоритм для разделения нерегулярных графов // ВЁсник ЗапорЁзького державного унЁверситету, 2002, ╧ 2, с. 1 – 10.
6. T. N. Bui, S. Chaudhuri, F. T. Leighton, M. Sipser. Graph bisection algorithms with good average case behavior // Combinatorica, 1987, N7, pp. 171.191.
7. L. Miller Gary, Teng Shang-Hua, A. Vavasis Stephen. A unified geometric approach to graph separators: Proceedings of 31st Annual Symposium on Foundations of Computer Science, 1991, pp. 538 -547.
8. М.Р. Когаловский. Перспективные технологии информационных систем. – М.: ДМК Пресс; М.: Компания АйТи, 2003. – 288 с.
9. G.A. Miller and etc. Wordnet: a lexical database for the english language [Электронныйресурс]. // (http://wordnet.princeton.edu/).
10. E. Gabrilovich, S. Markovitch. Computing semantic relatedness using wikipedia-based explicit semantic analysis: Proceedings of the Twentieth International Joint Conference on Artificial Intelligence (IJCAI-07), Hyderabad, India, January 6-12, 2007:AAAI Press, 2007, pp. 1606–1611.
11. Ю.А. Целых. Теоретико-графовые методы анализа нечетких социальных сетей [Электронный ресурс]. (http://swsys.ru/print/article_print.php?id=742).
12. B. Hendrickson, R. Leland. An improved spectral graph partitioning algorithm for mapping parallel computations. SandiaNationalLaboratories. -TechnicalReportSAND92-1460, 1992. –P. 192.
13. М. Гринева, Д. Лизоркин. Анализ текстовых документов для извлечения тематически сгруппированных ключевых терминов [Электронный ресурс]. (http://citforum.ru/database/articles/kw_extraction/).
14. М.Ю. Богатырев, В.Е. Латов, И.А. Столбовская. Применение концептуальных графов в системах поддержки электронных библиотек: Труды 9-ой Всероссийской научной конференции «Электронные библиотеки: перспективные методы и технологии, электронные коллекции» - RCDL’2007, Переславль-Залесский, Россия, 2007. – Т. 2, С. 104-110.
15. Л.И. Бородкин. Математические методы и компьютер в задачах атрибуции текстов [Электронный ресурс]. (http://www.textology.ru/library/book.aspx?bookId=11&textId=13).
16. Dmitry Lizorkin and etc. Accuracy Estimate and Optimization Techniques for SimRank Computation: Proceedings of the 34th International Conference on Very Large Data Bases (VLDB’08). – 2008. – Vol. 1, Issue 1. – pp. 422-433;
17. О.И. Ларичев. Теория и методы принятия решений, а также Хроника событий в Волшебных странах. – М.: Университетская книга, Логос, 2006. -292 с.
18. Hong Zhang, Masumi Ishikawa. Evolutionary Canonical Particle Swarm Optimizer - A Proposal of Meta-Optimization in Model Selection. Berlin : Springer-Verlag, 2008.
19. R. Mihalcea. Using Wikipedia for Automatic Word Sense Disambiguation: Proceedings of the North American Chapter of the Association for Computational Linguistics (NAACL 2007), Rochester, April 2007, pp. 196 - 203.
Публикации с ключевыми словами: семантическая сеть, онтология, релевантность
Публикации со словами: семантическая сеть, онтология, релевантность
Смотри также:
- Оценка релевантности документов корпоративной онтологической базы знаний на основе их иерархической ролевой кластеризации
- Некоторые методы огрубления графов при оценке релевантности документов
- Многокритериальная оценка релевантности документов корпоративной онтологической базы знаний на основе их ролевой кластеризации
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



