научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 07, июль 2010
УДК 519.87
gorelik@ccas.ru, akasana777@mail.ru
Московский педагогический государственный университет
Введение
Технические устройства занимают все более прочные позиции в жизни современного человека. Немалая часть их функционирует и управляется на основе комбинирования сигналов по принципу перестановок, размещений и сочетаний, являющихся предметом изучения комбинаторики. Для исследования и прогнозирования работы таких систем традиционно используют математическое и компьютерное моделирование. Как правило, рассмотрение возможных решений задач обработки сигналов и интерпретация ведется с помощью аппарата дискретной математики и геометрии [1]. В данной работе для получения более полной информационной картины работы структур, функционирующих по законам комбинаторики, предлагается использовать системы линейных уравнений и неравенств комбинаторного типа. Для этого вводится новое понятие матрицы комбинаторного типа.
Современные ЭВМ обладают высокой мощностью и могут выполнять большое количество вычислительных операций за малое время. И с каждым годом эти показатели растут. В этой связи видится возможным пересмотреть традиционный подход к математическому описанию моделей комбинаторных устройств. С точки зрения исследователя при таком подходе к обработке сигналов, полученных от устройств, работающих на комбинаторных принципах, появляется возможность всесторонне изучить модель, получать сведения не только о результатах работы, но и о факторах, существенно на нее влияющих, определять границы устойчивости. В случае противоречивости модели, описанной системой комбинаторного типа, имеется возможность применить методы коррекции систем линейных уравнений, с условием минимальности изменений исходных данных. В данной работе предлагается использовать в таких случаях алгоритм обобщенной наименьшей нормы (TLN).
1. Понятие систем уравнений и неравенств комбинаторного типа
Определение. Системой линейных уравнений комбинаторного типа назовем систему вида
![]()
где ![]() ,
, ![]() матрица
матрица ![]() имеет вид
имеет вид

![]() , первые n строк матрицы содержат по 1 ненулевому элементу и представляют сочетание из n элементов по 1 или, что то же самое, подмножества множества {1, …, n} состоящие из одного элемента, следующие
, первые n строк матрицы содержат по 1 ненулевому элементу и представляют сочетание из n элементов по 1 или, что то же самое, подмножества множества {1, …, n} состоящие из одного элемента, следующие ![]() строк содержат по 2 элемента и являются подмножествами множества {1, …, n}, состоящими из двух элементов и т.д. Последняя строка содержит все n элементов. Очевидно,
строк содержат по 2 элемента и являются подмножествами множества {1, …, n}, состоящими из двух элементов и т.д. Последняя строка содержит все n элементов. Очевидно, ![]() , где q – число элементов в подмножестве. Таким образом, строки матрицы представляют наборы лексикографически упорядоченных подмножеств множества {1, …, n}.
, где q – число элементов в подмножестве. Таким образом, строки матрицы представляют наборы лексикографически упорядоченных подмножеств множества {1, …, n}.
Обозначим множество матриц комбинаторного типа ![]() . В общем случае число ненулевых элементов матрицы A равно
. В общем случае число ненулевых элементов матрицы A равно ![]() , нулевых -
, нулевых - ![]() .
.
Соответственно, систему вида ![]() с теми же характеристиками матрицы
с теми же характеристиками матрицы ![]() и векторов
и векторов ![]() и
и ![]() будем называть системой линейных неравенств комбинаторного типа.
будем называть системой линейных неравенств комбинаторного типа.
С помощью таких систем можно описать работу большого числа различных вариантов технических схем, отличающихся не только структурой, но и числом и способом размещения элементов и соединения их между собой.
С увеличением мощности современных вычислительных машин появилась возможность проводить более объемные по количеству операций расчеты, делать переборы, ранее требовавшие сотни лет. Необходимо заметить, что так как матрицы комбинаторного типа имеют разреженную и однозначно задаваемую (по указанному ранее правилу) структуру, то нет необходимости хранить в памяти ЭВМ всю матрицу целиком и можно прибегнуть к операции векторизации.
Для ответа на вопрос о разрешимости системы уравнений комбинаторного типа легко проверить выполнение критерия Кронекера-Капелли, а для систем неравенств той же структуры можно предложить следующий критерий.
Теорема. Необходимым и достаточным условием совместности системы линейных неравенств комбинаторного типа вида ![]() для
для ![]() является выполнение условия
является выполнение условия
 ,
,
где ![]() ,
, ![]() .
.
Очевидно, что в общем случае комбинаторные системы несовместны (не имеют решения), т.к. являются примером переопределенных систем: ![]() .
.
2. Методы коррекции несовместных систем комбинаторного типа
В последние десятилетия получило развитие направление, связанное с исследованием несовместных (противоречивых) в классическом смысле моделей
[2] – [5]. Получены серьезные результаты в изучении проблемы коррекции несовместных систем линейных алгебраических уравнений [5]. Рассмотрим вопрос коррекции несовместных систем комбинаторного типа.
Наиболее изученным для систем произвольного типа является вопрос коррекции правой части системы уравнений, т. е. нахождения вектора ![]() такого, что система
такого, что система
![]()
имеет решение и ![]() .
.
Частным случаем такой коррекции является задача метода наименьших квадратов
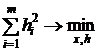
![]() ,
,
которая для систем комбинаторного типа решается с использованием псевдообратной матрицы, либо сингулярного разложения (особенно полезно при анализе влияния ошибок входной информации на решение задачи МНК), либо QR-алгоритма, суть которого заключается в разложении матрицы A в произведение ортогональной и верхней треугольной.
Нас в большей степени интересует вопрос коррекции левой части или обеих частей несовместной системы комбинаторного типа, которая позволяет более тонко управлять процессом с минимальными затратами и нивелировать воздействие присутствующих в системе шумов в показаниях как зависимых, так и независимых переменных. Рассмотрим решение следующей задачи.
Задача 1. Дана несовместная система линейных уравнений комбинаторного типа, записанная в матричном виде. Требуется найти матрицу H, имеющую ту же структуру, что и A и вектор ![]() такие, что система
такие, что система ![]() совместна и выполнено условие
совместна и выполнено условие
![]() ,
,
где ||×||E – евклидова норма.
Прежде всего, необходимо исследовать вопрос параметризации матрицы комбинаторного типа. Структура матрицы комбинаторного типа такова, что по полученному в результате параметризации вектору a размерности k она может быть однозначно восстановлена. Для таких матриц выполняется равенство
![]() .
.
Зная размеры ![]() и вектор a, можно однозначно построить матрицу H(a):
и вектор a, можно однозначно построить матрицу H(a):
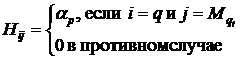 ,
,
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , M(t) – множество всех подмножеств индексов j, состоящих из t элементов, упорядоченное в лексикографическом порядке.
, M(t) – множество всех подмножеств индексов j, состоящих из t элементов, упорядоченное в лексикографическом порядке.
Данный факт позволяет в сформулированной задаче заменить понятие малости нормы матрицы на эквивалентное понятие – малость нормы вектора a, что в свою очередь дает возможность свести рассматриваемую задачу к задаче безусловной оптимизации.
Для линеаризации задачи 1 необходимо выполнить ряд матрично-векторных преобразований.
Поскольку H имеет ту же структуру, что и матрица A, то она имеет вид:
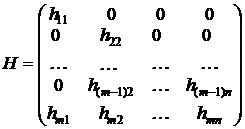 .
.
Матрица H однозначно определяется вектором ![]() . Использование записи H(a) подчеркивает, что матрица H – параметрическая, зависящая от a.
. Использование записи H(a) подчеркивает, что матрица H – параметрическая, зависящая от a.
Вектору x поставим в соответствие ![]() матрицу X(x) следующим образом:
матрицу X(x) следующим образом:
 .
.
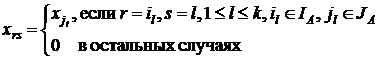
![]()
![]()
Параметрическая матрица X(x) позволяет получить тождество, связывающее x, a, H(a) и X(x):
![]() . (1)
. (1)
Предположим теперь, что некоторый вектор x и матрица H(a) заданы. Рассмотрим вектор невязок исследуемой системы линейных алгебраических уравнений комбинаторного типа
![]() . (2)
. (2)
Данное выражение фактически представляет собой вектор поправок правой части системы ![]() , такой что система
, такой что система ![]() совместна. Используя евклидову норму с учетом (2) и
совместна. Используя евклидову норму с учетом (2) и ![]() , задачу 1 можно сформулировать как задачу безусловной минимизации вида
, задачу 1 можно сформулировать как задачу безусловной минимизации вида
 . (3)
. (3)
Подвергнем векторы x и a линейным приращениям Da и Dx и рассмотрим вектор ![]() . В силу (1) выполняется
. В силу (1) выполняется ![]() . Отбрасывая слагаемое H(Da)Dx как величину второго порядка малости, получаем
. Отбрасывая слагаемое H(Da)Dx как величину второго порядка малости, получаем
![]() . (4)
. (4)
Используя соотношения (3) и (4), для решения задачи 1 применим алгоритм обобщенной наименьшей нормы (TLN-алгоритм) [6]
Вход: векторы ![]()
Выход: векторы aopt, xopt
1. Сформировать ![]()
2. Положить ![]() , сформировать X(x),
, сформировать X(x), ![]()
3. Повторять
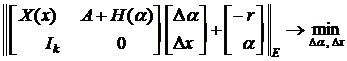
![]() ,
, ![]()
Сформировать H(a), X(x), ![]()
пока не выполнится ![]()
![]() .
.
Решение вспомогательной задачи минимизации, вычисляемое на каждом шаге алгоритма TLN находится с помощью метода наименьших квадратов, т. е., как уже говорилось, может быть решена либо с использованием псевдообращения матрицы
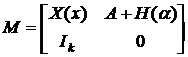 ,
,
либо с помощью сингулярного разложения, либо QR-разложения данной матрицы.
Рассмотрим теперь решение задачи коррекции несовместной системы неравенств комбинаторного типа.
Задача 2. Дана несовместная система линейных неравенств комбинаторного типа. При этом в общем случае ![]() . Требуется найти матрицу H и вектор
. Требуется найти матрицу H и вектор ![]() такие, что система
такие, что система ![]() совместна и выполнено условие
совместна и выполнено условие
![]()
Для начала приведем систему неравенств к системе уравнений:
![]()
Теперь требуется найти матрицу H размера ![]() , имеющую фиксированную комбинаторную структуру и вектор
, имеющую фиксированную комбинаторную структуру и вектор ![]() такие, что система
такие, что система
![]()
совместна и ![]() .
.
Предположим, что некоторый вектор x и матрица H(a) заданы. Рассмотрим вектор невязок исследуемой системы линейных алгебраических уравнений
![]() .
.
Исходная задача может быть сформулирована как задача условной минимизации вида
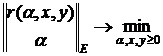 (4)
(4)
Так как ![]() , то
, то ![]() , а
, а ![]() . Подвергнув векторы x, y и a линейным приращениям Dx, Dy и Da, с учетом
. Подвергнув векторы x, y и a линейным приращениям Dx, Dy и Da, с учетом ![]() и отбрасывая слагаемое H(Da)Dx как величину второго порядка малости, получим:
и отбрасывая слагаемое H(Da)Dx как величину второго порядка малости, получим:
![]() . (5)
. (5)
Используя соотношения (4) и (5), для решения задачи 2 применим алгоритм обобщенной наименьшей нормы (TLN-алгоритм):
Вход: векторы ![]()
Выход: векторы aopt, yopt, xopt
1. Сформировать ![]()
2. Положить ![]() сформировать X(x),
сформировать X(x), ![]()
3. Повторять
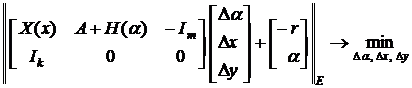
![]() ,
, ![]() ,
, ![]()
Сформировать H(a), X(x), ![]()
пока не выполнится ![]()
![]() ,
, ![]() .
.
Алгоритм TLN непосредственно не применим для задачи коррекции левой части системы, т. е. с условием h=0. Поэтому для решения такой задачи необходимо применить процедуру штрафования функции нормы вектора невязки.
Очевидно, что на практике встречаются различные условия функционирования структур комбинаторного вида, следовательно, и системы их описывающие также могут быть различными: смешанными, содержащими ограничения на коррекцию отдельных строк и столбцов и т.п. Мы рассмотрели базовые алгоритмы и преобразования, необходимые для работы таких алгоритмов. Рассмотрим теперь некоторые примеры применения таких систем.
3. Применение систем комбинаторного типа к задачам распознавания.
Одна из самых распространенных задач, которые человеку приходится решать в повседневной жизни – это распознавание образов (объектов, сигналов, явлений). Все чаще для решения этой задачи человек применяет технические средства. Соответственно возникает вопрос обучения устройства отделению по некоторым признакам одних объектов от других. Распознавание находит применение во многих видах деятельности: автоматическое чтение текстов, идентификация речи, задачи медицинской диагностики, геологического прогнозирования, оценки экономических и политических ситуаций, обнаружение и прогнозирование свойств химических соединений и другие. С точки зрения математики существенного различия в этих проблемах нет. В общем качественном виде задача сводится к следующей постановке: имеется некоторая совокупность объектов или явлений, в соответствии с выбранным принципом классификации она подразделена на ряд классов, разработан априорный словарь признаков, на языке которого описывается каждый класс, определена цель и описывающий ее показатель эффективности процесса распознавания. С учетом имеющихся ограничений по ресурсам и возможностям создания средств измерения признаков выбирается оптимальный набор признаков и строится алгоритм (решающее правило), позволяющий сопоставить апостериорные данные о неизвестном объекте с априорной информацией и на основе сопоставления определить, к какому классу он может быть отнесен.
Существуют разные модели решения классификационных задач [7]. Нас интересует модель, в которой разделение объектов на классы осуществляется с использованием разделяющей гиперплоскости.
Сформулируем проблему построения разделяющей гиперплоскости на примере разделения объектов двух классов.
Пусть в пространстве ![]() заданы w точек, относящихся к двум различным классам K1 и K2:
заданы w точек, относящихся к двум различным классам K1 и K2: ![]() ,
, ![]() ,
, ![]() . . Требуется построить для двух данных множеств разделяющую гиперплоскость вида
. . Требуется построить для двух данных множеств разделяющую гиперплоскость вида

(если объект принадлежит классу K1 выполняется ![]() , если
, если ![]() , то
, то ![]() ), т. е. найти коэффициенты
), т. е. найти коэффициенты ![]() такие, что
такие, что
![]()
![]()
Таким образом, имеем систему, совместность которой говорит о существовании разделяющей гиперплоскости.
Предположим теперь, что необходимо построить гиперплоскость вида 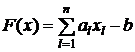 , разделяющую два данных множества с учетом возможного отсутствия некоторых значений параметров в задании объектов. Рассмотрим первый объект, относящийся к классу K1, во всевозможных подпространствах n-мерного пространства (всего их
, разделяющую два данных множества с учетом возможного отсутствия некоторых значений параметров в задании объектов. Рассмотрим первый объект, относящийся к классу K1, во всевозможных подпространствах n-мерного пространства (всего их ![]() ). Предположим, что при отсутствии измерений некоторых признаков, их значения полагаются равными нулю, что идентично операции проектирования на соответствующее подпространство. Будем формулировать задачу кластеризации таким образом, чтобы одно решающее правило работало во всех подпространствах признакового пространства, включая его самого. Тогда для отделения объекта необходимо решить относительно вектора a и числа b систему комбинаторного типа вида:
). Предположим, что при отсутствии измерений некоторых признаков, их значения полагаются равными нулю, что идентично операции проектирования на соответствующее подпространство. Будем формулировать задачу кластеризации таким образом, чтобы одно решающее правило работало во всех подпространствах признакового пространства, включая его самого. Тогда для отделения объекта необходимо решить относительно вектора a и числа b систему комбинаторного типа вида:

Построив для каждого объекта из представленной выборки такую систему, получим систему следующего вида:
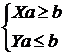 , (6)
, (6)
где 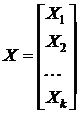 ,
, 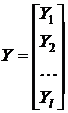 , Xi – матрицы комбинаторного типа, содержащие координаты i-го объекта класса K1, Yj – аналогичные матрицы для класса K2,
, Xi – матрицы комбинаторного типа, содержащие координаты i-го объекта класса K1, Yj – аналогичные матрицы для класса K2, ![]() .
.
Необходимо найти коэффициенты ![]() такие, что система (6) является совместной.
такие, что система (6) является совместной.
Каждая матрица Xi, Yj содержит в общем случае ![]() строк, следовательно, всего в системе (6) будет содержаться
строк, следовательно, всего в системе (6) будет содержаться ![]() неравенств. Таким образом, имеем переопределенную систему линейных неравенств комбинаторного типа. В случае совместности данной системы, можно говорить о существовании гиперплоскости с заданными свойствами. Однако наиболее вероятным видится случай, когда подобная система неравенств будет противоречива. Рассматривая задачу коррекции для такой системы, с помощью стандартного перехода от ограничений-неравенств к равенствам придем к системе линейных уравнений комбинаторного типа, для которой алгоритм нахождения минимальной матрицы и вектора коррекции был предложен ранее. В данной задаче имеем дополнительные ограничения на коррекцию: система (6) состоит из
неравенств. Таким образом, имеем переопределенную систему линейных неравенств комбинаторного типа. В случае совместности данной системы, можно говорить о существовании гиперплоскости с заданными свойствами. Однако наиболее вероятным видится случай, когда подобная система неравенств будет противоречива. Рассматривая задачу коррекции для такой системы, с помощью стандартного перехода от ограничений-неравенств к равенствам придем к системе линейных уравнений комбинаторного типа, для которой алгоритм нахождения минимальной матрицы и вектора коррекции был предложен ранее. В данной задаче имеем дополнительные ограничения на коррекцию: система (6) состоит из ![]() блоков по
блоков по ![]() строк. В каждом блоке имеем матрицу комбинаторного типа, в столбцах которой, в отличие от случая, рассмотренного ранее, находятся равные значения коэффициентов. Этому ограничению есть очевидное геометрическое объяснение: объекты выборки - суть точки n-мерного пространства, параметры (признаки) xij – координаты, очевидно, что каждая координата объекта определяется однозначно. Следовательно, в результате коррекции должны получить матрицу
строк. В каждом блоке имеем матрицу комбинаторного типа, в столбцах которой, в отличие от случая, рассмотренного ранее, находятся равные значения коэффициентов. Этому ограничению есть очевидное геометрическое объяснение: объекты выборки - суть точки n-мерного пространства, параметры (признаки) xij – координаты, очевидно, что каждая координата объекта определяется однозначно. Следовательно, в результате коррекции должны получить матрицу ![]() с теми же свойствами (т. е. и матрица коррекции H должна соответствовать указанным ограничениям, которые примем как условия на коррекцию).
с теми же свойствами (т. е. и матрица коррекции H должна соответствовать указанным ограничениям, которые примем как условия на коррекцию).
Таким образом, получаем новую задачу коррекции системы комбинаторного типа:
Дана несовместная система (6), которую запишем в виде:
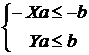
Необходимо найти матрицу 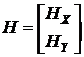 размера
размера ![]() и вектор
и вектор 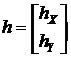 размера
размера ![]() , где
, где 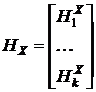 ,
, 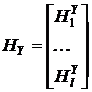 ,
, 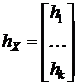 ,
, 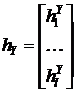 ,
, ![]() ,
, ![]() ,
,![]() такие, что система
такие, что система
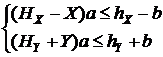
совместна и выполнено условие
![]() .
.
Решить такую задачу можно с помощью описанного ранее алгоритма обобщенной наименьшей нормы для системы линейных неравенств комбинаторного типа.
Заключение
Для математического моделирования работы некоторых технических устройств может использоваться понятие системы комбинаторного типа. Такие системы являются примером переопределенных систем и с большой вероятностью могут оказаться несовместными. Причинами несовместности любой модели могут быть неточность или неопределенность исходных данных, чрезмерное упрощение действительных связей, абсолютизация некоторых требований и другие причины. Противоречивость можно считать одним из факторов плохой формализуемости, которая является частым атрибутом реальных задач. Несовместная модель может быть отражением существующих противоречий, а способы ее корректирования – отражением действительных процедур разрешения реальных проблем.
Использование систем комбинаторного типа и возможности коррекции позволяют описывать взаимодействие различных объектов и на основе такого моделирования получать прогнозы и детальную картину влияний отдельных факторов (обнаруживать и предсказывать направления для устранения помех), получать информацию о минимальных затратах, которые необходимо осуществить для устранения проблемы.
Литература
1. Кувырков П.П., Темников Ф.Е. Комбинаторные системы. М.: Энергия, 1975. 152 с.
2. Еремин И.И., Мазуров В.Д., Астафьев Н.Н. Несобственные задачи линейного и выпуклого программирования. М.: Наука, 1983. 334 с.
3. Ватолин А.А. Несобственные задачи математического программирования и методы их коррекции: Дисс. … д-ра физ.-мат. наук. Екатеринбург, 1992. 232 с.
4. Горелик В.А., Ерохин В.И. Оптимальная матричная коррекция несовместных систем линейных алгебраических уравнений по минимуму евклидовой нормы. М.: ВЦ РАН, 2004. 193 с.
5. Горелик В.А., Ерохин В.И., Печенкин Р.В. Численные методы коррекции несобственных задач линейного программирования и структурных систем уравнений. М.: ВЦ РАН, 2006. 150 с.
6. Rosen J.B., Park H., Glick J. Structured nonlinear total least norm problems // UMSI reserch report. Minniapolis (Mn): Univ. of Minnesota. Supercomput. inst., 1995, 95/152, 11 p.
7. Журавлев Ю.И. Избранные научные труды. М.: Магистр, 1998. 420 с.
Публикации с ключевыми словами: компьютерное моделирование, комбинаторика
Публикации со словами: компьютерное моделирование, комбинаторика
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



