научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 06, июнь 2010
DOI: 10.7463/0610.0143964
dmitry_moor@mail.ru
karpenko@nog.ru
D.Mukhlisullina@mail.ru
МГТУ им. Н.Э.Баумана
Введение
В задаче многокритериальной оптимизации, или задаче многокритериального принятия решений (МКО-задачи) предполагается заданной вектор-функция ![]() , которая определена на множестве допустимых значений (множестве альтернатив)
, которая определена на множестве допустимых значений (множестве альтернатив) ![]() вектора варьируемых параметров X. Лицу, принимающему решение (ЛПР), желательно найти такую альтернативу, которая минимизирует (для определенности) все компоненты этой вектор-функции
вектора варьируемых параметров X. Лицу, принимающему решение (ЛПР), желательно найти такую альтернативу, которая минимизирует (для определенности) все компоненты этой вектор-функции ![]() , называемые частными критериями оптимальности.
, называемые частными критериями оптимальности.
В статье рассматривается метод решения МКО-задачи, который относится к классу адаптивных методов [1]. Каждая итерация этих методов включает в себя фазу анализа, выполняемую ЛПР, и фазу расчетов, выполняемую системой многокритериальной оптимизации (МКО-системой).
По характеру информации, получаемой МКО-системой от ЛПР на фазе анализа, выделяются несколько классов адаптивных методов. В даннойработе рассматриваются прямые адаптивные методы [1]. Эти методы основаны на том, что ЛПР может непосредственно выполнять оценку предлагаемых МКО-системой альтернатив (например, в терминах «лучше», «хуже», «одинаково»).
В основе прямых адаптивных методов решения МКО-задачи, лежит предположение о существовании «функции предпочтений ЛПР»![]() . Эта функция определена на множестве
. Эта функция определена на множестве![]() и выполняет его отображение на множество действительных чисел R. При этом задача многокритериальной оптимизации сводится к выбора вектора
и выполняет его отображение на множество действительных чисел R. При этом задача многокритериальной оптимизации сводится к выбора вектора ![]() такого, что
такого, что
![]() ,
, ![]() .
.
Предполагается, что при предъявлении ЛПР вектора параметров X, а также соответствующих значений всех частных критериев оптимальности ![]() , ЛПР может оценить соответствующее значение своейфункции предпочтений
, ЛПР может оценить соответствующее значение своейфункции предпочтений ![]() .
.
В работе [2] предложен класс прямых адаптивных методов решения МКО-задачи, основанных на аппроксимации функции предпочтений ЛПР ![]() . Использование нейронных сетей для аппроксимации функции
. Использование нейронных сетей для аппроксимации функции ![]() рассмотрено в работах [3, 4]. В данной работе аппроксимация функции предпочтений ЛПР
рассмотрено в работах [3, 4]. В данной работе аппроксимация функции предпочтений ЛПР ![]() выполняется с помощью аппарата нейро-нечеткого вывода ANFIS (AdaptiveNeuro-FuzzyInferenceSystem) [5].
выполняется с помощью аппарата нейро-нечеткого вывода ANFIS (AdaptiveNeuro-FuzzyInferenceSystem) [5].
Гибридные нейро-нечеткие системы находят существенно более широкую область применения, чем другие методы синтеза нечетких множеств и нейронных сетей [5]. Это связано с тем, что такие системы позволяют наиболее полно использовать «сильные» стороны нечетких систем (интерпретируемость накопленных знаний) и нейронных сетей (способность обучаться на данных). Характерной чертой гибридных систем является то, что они всегда могут быть рассмотрены как системы нечетких правил, при этом настройка функций принадлежности в предпосылках и заключениях правил на основе обучающего множества производится с использованием алгоритмов обучения нейронных сетей. Такие системы не только используют априорную информацию, но могут приобретать новые знания, являясь логически «прозрачными».
В первом разделе работы приводится постановка МКО-задачи. Во втором разделе представленасхема метода решения задачи. В третьем разделе обсуждается алгоритм и программная реализация метода. Четвертый раздел посвящен исследованию эффективности нейро-нечеткой аппроксимации функции предпочтений ЛПР. В заключение формулируются основные выводы.
1 Постановка МКО-задачи
Пусть X - вектор варьируемых параметров задачи. Множеством допустимых значений вектора Xявляется ограниченное и замкнутое множество ![]() , где
, где ![]() - «технологический» параллелепипед допустимых значений вектора параметров; множество
- «технологический» параллелепипед допустимых значений вектора параметров; множество ![]() формируют ограничивающие функции
формируют ограничивающие функции ![]() , так что
, так что ![]() ;
; ![]() - n-мерное арифметическое пространство.
- n-мерное арифметическое пространство.
Векторный критерий оптимальности ![]() со значениями в критериальном пространстве
со значениями в критериальном пространстве ![]() определен в параллелепипеде П. ЛПР стремится минимизировать на множестве
определен в параллелепипеде П. ЛПР стремится минимизировать на множестве ![]() каждый из частных критериев оптимальности
каждый из частных критериев оптимальности ![]() , что условно записывается в виде
, что условно записывается в виде
![]() ,
, ![]() , (1)
, (1)
где ![]() - искомое решение МКО-задачи. Полагаем, что все частные критерии оптимальности тем или иным образом нормализованы, так что
- искомое решение МКО-задачи. Полагаем, что все частные критерии оптимальности тем или иным образом нормализованы, так что![]() ,
, ![]() .
.
Обозначим ![]() операцию свертки частных критериев оптимальности, где
операцию свертки частных критериев оптимальности, где ![]() - вектор весовых множителей;
- вектор весовых множителей; ![]()
![]() - множество допустимых значений этого вектора.
- множество допустимых значений этого вектора.
При каждом фиксированном векторе ![]() метод скалярной свертки сводит решение задачи (1) к решению однокритериальной задачи глобальной условной оптимизации (ОКО-задачи)
метод скалярной свертки сводит решение задачи (1) к решению однокритериальной задачи глобальной условной оптимизации (ОКО-задачи)
![]() ,
, ![]() . (2)
. (2)
Отметим, что в случае аддитивной свертки ![]() вектор
вектор ![]() принадлежит множеству эффективных по Парето векторов [1]. Для произвольной скалярной свертки вектор
принадлежит множеству эффективных по Парето векторов [1]. Для произвольной скалярной свертки вектор ![]() , полученный в результате решения задачи (2), вообще говоря, не принадлежит множеству Парето.
, полученный в результате решения задачи (2), вообще говоря, не принадлежит множеству Парето.
Обозначим ![]() - критериальное множество (множество достижимости) задачи, т.е. множество, в которое векторный критерий оптимальности отображает множество
- критериальное множество (множество достижимости) задачи, т.е. множество, в которое векторный критерий оптимальности отображает множество ![]() . Ограничимся случаем, когда множество достижимости
. Ограничимся случаем, когда множество достижимости ![]() задачи (1) является выпуклым. Тогда при каждом
задачи (1) является выпуклым. Тогда при каждом ![]() решение задачи (2) единственно, и это условие (2) ставит в соответствие каждому из допустимых векторов
решение задачи (2) единственно, и это условие (2) ставит в соответствие каждому из допустимых векторов ![]() единственный вектор
единственный вектор ![]() , а также соответствующие значения частных критериев оптимальности
, а также соответствующие значения частных критериев оптимальности ![]() [1]. Данное обстоятельство позволяет полагать, что функция предпочтений ЛПР определена не на множестве
[1]. Данное обстоятельство позволяет полагать, что функция предпочтений ЛПР определена не на множестве ![]() , а на множестве
, а на множестве ![]() :
:
![]() .
.
В результате МКО-задача сводится к задаче выбора вектора ![]() такого, что
такого, что
![]() ,
, ![]() . (3)
. (3)
Поскольку обычно ![]() , переход от задачи (1) к задаче (3) важен с точки зрения уменьшения вычислительных затрат.
, переход от задачи (1) к задаче (3) важен с точки зрения уменьшения вычислительных затрат.
Если используется аддитивная свертка и множество достижимости ![]() является выпуклым, то выражение (2) задает взаимно однозначное отображение множества
является выпуклым, то выражение (2) задает взаимно однозначное отображение множества ![]() на фронт Парето задачи
на фронт Парето задачи ![]() [1]. При этом, как отмечалось, для любого
[1]. При этом, как отмечалось, для любого ![]() вектор
вектор ![]() , являющийся решением задачи (2), принадлежит множеству Парето
, являющийся решением задачи (2), принадлежит множеству Парето ![]() .
.
Отметим, что если вместо аддитивной свертки используется свертка Джоффриона, то взаимно однозначное отображение множества ![]() на множество
на множество ![]() имеет место и в случае, когда множество достижимости
имеет место и в случае, когда множество достижимости ![]() не является выпуклым [6].
не является выпуклым [6].
Величину ![]() будем считать лингвистической переменной со значениями от «Очень-очень плохо» до «Отлично». Ядро нечеткой переменной
будем считать лингвистической переменной со значениями от «Очень-очень плохо» до «Отлично». Ядро нечеткой переменной ![]() обозначим
обозначим ![]() , так что значению переменной
, так что значению переменной ![]() «Очень-очень плохо» соответствует
«Очень-очень плохо» соответствует ![]() , а значению «Отлично» -
, а значению «Отлично» - ![]() .
.
В результате МКО-задача сводится к задаче отыскания вектора ![]() , обеспечивающего максимальное значение дискретной функции
, обеспечивающего максимальное значение дискретной функции ![]() :
:
![]() ,
, ![]() . (4)
. (4)
2 Метод решения задачи
Общая схема рассматриваемого метода является итерационной и состоит из следующих основных этапов [7].
Этап «разгона» метода. МКО-система некоторым образом (например, случайно) последовательно генерирует ![]() векторов
векторов ![]() и для каждого из этих векторов выполняет следующие действия:
и для каждого из этих векторов выполняет следующие действия:
1) решает ОКО-задачу
![]() ,
, ![]() ,
, ![]() ; (5)
; (5)
2) предъявляет ЛПР найденное решение ![]() , а также соответствующие значение всех частных критериев оптимальности
, а также соответствующие значение всех частных критериев оптимальности ![]() ;
;
3) ЛПР оценивает эти данные и вводит в МКО-систему соответствующее значение своей функции предпочтений ![]() .
.
Первый этап. На основе всех имеющихся в МКО-системе значений ![]() вектора
вектора ![]() и соответствующих оценок функции предпочтений
и соответствующих оценок функции предпочтений ![]() МКО-система выполняет следующие действия:
МКО-система выполняет следующие действия:
1) строит функцию ![]() , аппроксимирующую функцию
, аппроксимирующую функцию ![]() в окрестности точек
в окрестности точек ![]() ;
;
2) отыскивает максимум функции ![]() – решает задачу
– решает задачу
![]() ,
, ![]() ;
;
3) с найденным вектором ![]() решает ОКО-задачу вида (5) – находит вектор параметров и соответствующие значения частных критериев оптимальности, а затем предъявляет их ЛПР; ЛПР оценивает указанные данные и вводит в систему соответствующее значение своей функции предпочтений
решает ОКО-задачу вида (5) – находит вектор параметров и соответствующие значения частных критериев оптимальности, а затем предъявляет их ЛПР; ЛПР оценивает указанные данные и вводит в систему соответствующее значение своей функции предпочтений ![]() .
.
Второй этап. На основе всех имеющихся в системе значений ![]() вектора
вектора ![]() и соответствующих оценок функции предпочтений
и соответствующих оценок функции предпочтений ![]() МКО-система выполняет аппроксимацию функции
МКО-система выполняет аппроксимацию функции ![]() в окрестности точек
в окрестности точек ![]() - строит функцию
- строит функцию ![]() и т.д. по схеме первого этапа до тех пор, пока ЛПР не примет решение о прекращении вычислений.
и т.д. по схеме первого этапа до тех пор, пока ЛПР не примет решение о прекращении вычислений.
На каждой итерации ЛПР может выполнить «откат» с целью изменения введенных ранее оценок своей функции предпочтений [3].
3 Алгоритм и программная реализация метода
Входами системы нечеткого вывода являются значения весов частных критериев оптимальности – нечеткие термы ![]() ,
, ![]() ,
, ![]() . Выходной переменной системы нечеткого вывода является лингвистическая переменная
. Выходной переменной системы нечеткого вывода является лингвистическая переменная ![]() , ядро которой
, ядро которой ![]() принимает значения 1, 2,…, 9.
принимает значения 1, 2,…, 9.
Взаимосвязь между входными и выходными переменными описывается нечеткими правилами вида
ЕСЛИ <значения входных переменных>, ТО
<значение выходной переменной>.
Совокупность значений указанных нечетких входных переменных, выходных лингвистических переменных, а также правил нечетких продукций образуют нечеткую базу знаний.
Используется адаптивная нейро-нечеткая система вывода ANFIS, функционально эквивалентная системам нечеткого вывода Сугено. Вывод выполняется за два шага. На первом шаге осуществляется формирование базы знаний и системы нечеткого вывода Сугено, а также грубая настройка модели ![]() . На втором шаге производится тонкая настройка модели
. На втором шаге производится тонкая настройка модели ![]() , заключающаяся в подборе таких параметров функций принадлежности, которые минимизируют различие между экспериментальной и желаемой» моделями.
, заключающаяся в подборе таких параметров функций принадлежности, которые минимизируют различие между экспериментальной и желаемой» моделями.
3.1 Формирование базы знаний и системы нечеткого вывода Сугено. Положим, что выполнено N экспериментов по определению значений лингвистической переменной ![]() . Пусть в
. Пусть в ![]() этих экспериментов переменная
этих экспериментов переменная ![]() приняла значение
приняла значение ![]() , в
, в ![]() опытах - значение
опытах - значение ![]() и т.д. до
и т.д. до ![]() и
и ![]() . Соответствующие входные векторы
. Соответствующие входные векторы ![]() обозначим
обозначим ![]() , где
, где ![]() ,
, ![]() .
.
Матрицу знаний ![]() можно представить в виде следующей системы логических высказываний
можно представить в виде следующей системы логических высказываний
ЕСЛИ ![]() и
и ![]() И … И
И … И ![]() ИЛИ
ИЛИ
![]() и
и ![]() И … И
И … И ![]() ИЛИ
ИЛИ
……….
![]() И
И ![]() И … И
И … И ![]() , ТО
, ТО ![]() .
.
С использованием операций объединения и пересечения множеств эта система высказываний может быть переписана в более компактном виде
![]() ,
, ![]() .
.
База знаний Сугено отличается от базы знаний Мамдани лишь тем, что заключения правил задаются не нечеткими термами, а линейной функцией входов [5].
Во введенных обозначениях нечеткий логический вывод Сугено включает в себя следующие операции.
1) Фаззификация. Для данного вектора ![]() определяем значение многомерной функции принадлежности
определяем значение многомерной функции принадлежности
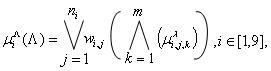
где ![]() - веса нечетких правил;
- веса нечетких правил; ![]() - символы логических операций «ИЛИ», «И»;
- символы логических операций «ИЛИ», «И»; ![]() - функция принадлежности весового множителя
- функция принадлежности весового множителя ![]() терму
терму ![]() .
.
2) Агрегирование – это операция определения степени истинности условий по каждому из правил системы нечеткого вывода. При вычислении значений функции принадлежности ![]() в качестве операций «И», «ИЛИ», «импликация» используем операции prod, max, min соответственно.
в качестве операций «И», «ИЛИ», «импликация» используем операции prod, max, min соответственно.
3) Активизация - нахождение степени истинности каждого из подзаключений правил нечетких продукций. Во-первых, находятся значения степеней истинности ![]() всех заключений правил нечетких продукций. Это выполняется с использованием метода min-активизации. Во-вторых, осуществляется расчет обычных (не нечетких) значений выходных переменных каждого правила.
всех заключений правил нечетких продукций. Это выполняется с использованием метода min-активизации. Во-вторых, осуществляется расчет обычных (не нечетких) значений выходных переменных каждого правила.
4) Аккумуляция - нахождение функции принадлежности для каждой из выходных лингвистических переменных. В данной задаче эта операция фактически отсутствует, поскольку расчеты осуществляются с обычными действительными числами ![]() .
.
5) Дефаззификация - нахождение обычного (не нечеткого) значения для каждой из выходных лингвистических переменных. Для дефаззификации используется метод центра тяжести для одноточечных множеств:
 .
.
Здесь n – общее количество активных правил нечетких продукций, в подзаключениях у которых присутствует выходная лингвистическая переменная ![]() .
.
3.2 Настройка параметров функций принадлежности. Тонкая настройка модели ![]() (параметрическая идентификация модели) заключается в настройке параметров функций принадлежности на основе обучающего множества с помощью нейронных сетей.
(параметрическая идентификация модели) заключается в настройке параметров функций принадлежности на основе обучающего множества с помощью нейронных сетей.
Система вывода ANFIS реализуется в виде нейроподобной структуры, состоящей из пяти слоев (рис. 1).
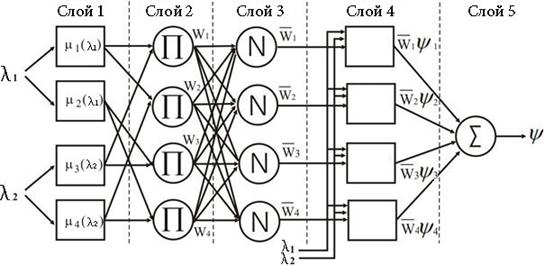
Рис. 1. Структура нейро-нечеткой сети ANFIS
Нейроны первого слоя служат для представления термов входных переменных. При конкретных (заданных) значениях входов на выходе слоя формируются значения функций принадлежности ![]() .
.
Нейроны второго слоя исполняют роль антецедентов (посылок) нечетких правил. Выходами этого слоя являются степени истинности предпосылок ![]() каждого правила базы знаний системы.
каждого правила базы знаний системы.
Нейроны третьего слоя служат для нормализации степеней выполнения правил. Выход ![]() i-го нейрона этого слоя представляет собой отношение степени истинности предпосылки i-го правила к сумме степеней предпосылок всех правил.
i-го нейрона этого слоя представляет собой отношение степени истинности предпосылки i-го правила к сумме степеней предпосылок всех правил.
Четвертый слой предназначен для вычисления заключений правил. Здесь
![]() ,
,
где ![]() – набор параметров данного слоя (так называемые параметры вывода).
– набор параметров данного слоя (так называемые параметры вывода).
Пятый слой выполняет агрегирование результата, полученного по различным правилам. Единственный нейрон этого слоя вычисляет выходное значение сети.
Для обучения сети ANFIS в работе используется гибридный градиентный метод_[5].
Для оценки погрешности нечеткой нейронной сети строится функция ошибки
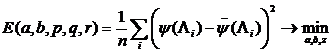 ,
, ![]() , (6)
, (6)
представляющая собой среднеквадратическое отклонение между фактическими значениями выходной переменной ![]() и точечной оценкой
и точечной оценкой ![]() , полученной на основе нечеткого вывода. Здесь a, b – параметры функций принадлежности первого слоя нечеткой нейронной сети; p, q, r– параметры четвертого слоя нечеткой нейронной сети.
, полученной на основе нечеткого вывода. Здесь a, b – параметры функций принадлежности первого слоя нечеткой нейронной сети; p, q, r– параметры четвертого слоя нечеткой нейронной сети.
3.3 Генерация нечетких правил. В процессе решения задачи система вывода ANFISимеет возможность приобретать новые знания, поэтому база знаний не остается фиксированной, а модернизируется по мере поступления экспериментальных данных. Поэтому топология нечеткой нейронной сети также меняется по мере приобретения новых знаний. Для модификации топологии нечеткой нейронной сети используется процедура, предложенная в работе [5].
Пусть исследуемый объект имеет на входе n-мерный вектор ![]() , на выходе - число y. Пусть кроме того «истинное» описание объекта имеет вид
, на выходе - число y. Пусть кроме того «истинное» описание объекта имеет вид
![]() ,
,
где f(x) – неизвестная функция, e– случайная аддитивная помеха. Предположим, что может быть реализован эксперимент, заключающийся в регистрации Nнаборов значений ![]() , i=1,…,N. При этом компоненты вектора x, измеряются без ошибок, значение величины N при необходимости допускает модификацию.
, i=1,…,N. При этом компоненты вектора x, измеряются без ошибок, значение величины N при необходимости допускает модификацию.
Алгоритм построения системы вывода ANFISимеет следующий вид.
ШАГ 1. Из m, (m < N) произвольных наборов значений ![]() составляется начальная база знаний модели.
составляется начальная база знаний модели.
![]()
ШАГ 2. Для каждого нового экспериментального набора ![]() определяется прогнозируемое значение
определяется прогнозируемое значение ![]() величины y.
величины y.
ШАГ 3. Проверяется неравенство
![]() ,
,
где ![]() – заданная константа, определяющая погрешность аппроксимации. При выполнении неравенства база знаний системы пополняется.
– заданная константа, определяющая погрешность аппроксимации. При выполнении неравенства база знаний системы пополняется.
ШАГ 4. Проверяется выполнение правила останова. Если это правило выполнено, то алгоритм завершается; если правило не выполнено, алгоритм переходит к шагу 2.
4 Оценка эффективности метода
Исследование выполнено для двух двумерных двухкритериальных задач и одной трехмерной трехкритериальной тестовых задач.
Задача 1. Двухкритериальная задача 1, имеющая выпуклый фронт Парето:
![]() ;
; ![]() ;
;
![]() .
.
Задача 2. Двухкритериальная задача 2 (невыпуклый фронт Парето) [8]:
![]() ;
; 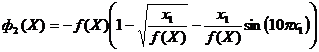 ;
;
![]() ;
;
![]() .
.
Задача 3. Трехкритериальная задача 3 (выпуклый фронт Парето):
![]() ;
; ![]() ;
;
![]() ;
;
![]() .
.
Частные критерии оптимальности нормализованы следующим образом:
![]() .
.
Здесь ![]() ,
, ![]() ;
; ![]() ,
, ![]() .
.
Приняты следующие обозначения:
· ![]() ,
, ![]() - время решения задачи (2) и (3) соответственно;
- время решения задачи (2) и (3) соответственно;
· ![]() - прочее время;
- прочее время;
· ![]() - время выполнения одной итерации метода,
- время выполнения одной итерации метода, ![]() =
=![]() +
+![]() +
+![]() ;
;
· ![]() -ошибка аппроксимации, вычисляемая по формуле (6).
-ошибка аппроксимации, вычисляемая по формуле (6).
Эксперименты выполнены на персональном компьютере, имеющем следующие значения основных параметров: процессор - IntelCore2 DuoE8400; 3.00 ГГц; оперативная память - 2.00 Гбайт.
4.1 Задача 1 (МКО-задача 1). Критериальное множество МКО-задачи 1 представлено на рис. 2. Исследование выполнено для ![]() «разгонных» значений
«разгонных» значений ![]() вектора
вектора ![]() . В процессе экспериментов ЛПР полагало, что «отличным» значениям его функции предпочтений соответствуют следующие значения критериев оптимальности:
. В процессе экспериментов ЛПР полагало, что «отличным» значениям его функции предпочтений соответствуют следующие значения критериев оптимальности: ![]() ,
, ![]() .
.
Процесс решения задачи иллюстрирует таблица 1, где ![]() - номер итерации, серым цветом выделены «разгонные» итерации;
- номер итерации, серым цветом выделены «разгонные» итерации; ![]() .
.
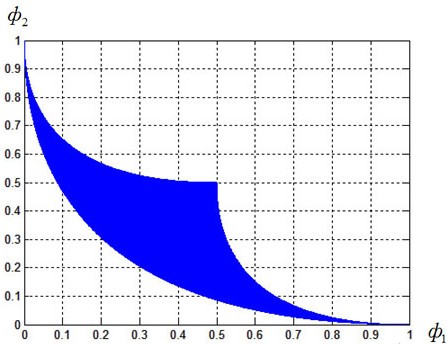
Рис. 2. Множество достижимости ![]() МКО-задачи 1
МКО-задачи 1
Вид функции ![]() после 7 итераций представляет рис. 3. Здесь и далее светлые кружки соответствуют значениям функции предпочтений ЛПР на промежуточных итерациях метода, которые образуют правые части нечеткой базы знаний.
после 7 итераций представляет рис. 3. Здесь и далее светлые кружки соответствуют значениям функции предпочтений ЛПР на промежуточных итерациях метода, которые образуют правые части нечеткой базы знаний.
Таблица 1. Результаты решения МКО-задачи 1
|
|
|
|
|
|
|
|
|
1 | 0.00 | 0.97 | 0.00 | 1 | 1.47 |
|
|
|
2 | 0.79 | 0.04 | 0.63 | 4 | 1.48 |
|
|
|
3 | 0.55 | 0.20 | 0.30 | 9 | 1.48 |
|
|
|
4 | 0.65 | 0.11 | 0.42 | 7 | 1.49 | 6.12 | 7.65 | 0 |
5 | 0.55 | 0.19 | 0.30 | 9 | 1.48 | 4.84 | 6.34 | 0 |
6 | 0.55 | 0.19 | 0.30 | 9 | 1.50 | 5.50 | 7.03 | 0 |
7 | 0.55 | 0.19 | 0.30 | 9 | 1.46 | 5.98 | 7.49 | 0 |
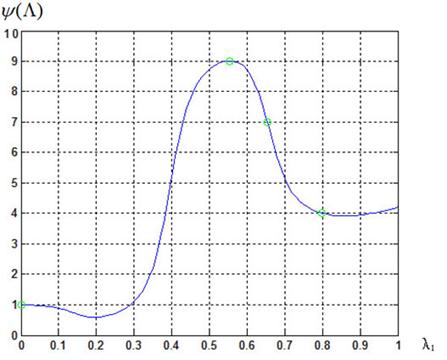
Рис. 3. Функция предпочтений ЛПР ![]() :
:
МКО-задача 1; число «разгонных» точек ![]() ; 7-я итерация
; 7-я итерация
Оптимальное решение было найдено всего за пять итераций (в этой и последующих задачах в число итераций включаются и «разгонные» итерации). Отметим, что висследовании [7] оптимальное решение этой же задачи было найдено за восемь итераций.
На рис. 4 представлена структура полученной нейро-нечеткой сети ANFIS. Здесь и далее для удобства слой 2 и слой 3 (см. рис. 1) объединены в один слой, узлы которого показаны синими кружками.
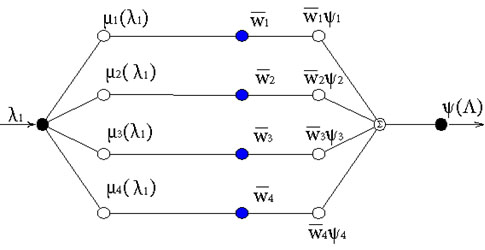
Рис. 4. Структура нейро-нечеткой сети ANFIS
4.2 Задача 2 (МКО-задача 2). На рис. 5 представлено критериальное множество МКО-задачи 2. В процессе экспериментов ЛПР полагало, что «отличным» значениям его функции предпочтений соответствуют следующие значения критериев оптимальности: ![]() ,
, ![]() .
.

Рис. 5. Множество достижимости ![]() МКО-задачи 2
МКО-задачи 2
Решение этой задачи потребовало семь итераций (для сравнения, в работе [7] для этого потребовалось 11 итераций). Процесс решения задачи иллюстрирует таблица 2, а результат решения – рис. 6. В данной задаче количество узлов первого слоя получилось равным семи (рис. 7).
Таблица 2. Результаты решения МКО-задачи 2
|
|
|
|
|
|
|
|
|
1 | 0.24 | 0.04 | 0.19 | 6 | 2.12 |
|
|
|
2 | 0.00 | 1.00 | 0.00 | 1 | 1.97 |
|
|
|
3 | 0.57 | 0.03 | 0.20 | 7 | 2.73 |
|
|
|
4 | 1.00 | 0.00 | 0.29 | 2 | 1.34 | 6.34 | 7.75 | 0 |
5 | 0.76 | 0.00 | 0.29 | 3 | 3.22 | 4.30 | 7.56 | 0 |
6 | 0.64 | 0.02 | 0.21 | 8 | 2.62 | 4.08 | 6.72 | 0 |
7 | 0.67 | 0.02 | 0.22 | 9 | 3.04 | 3.37 | 6.44 | 0 |
8 | 0.70 | 0.02 | 0.23 | 9 | 2.58 | 4.21 | 6.82 | 0 |
9 | 0.69 | 0.02 | 0.23 | 9 | 2.74 | 3.93 | 6.71 | 0.0040 |
10 | 0.69 | 0.02 | 0.23 | 9 | 2.80 | 3.36 | 6.20 | 0.0172 |

Рис. 6. Функция предпочтений ЛПР ![]() :
:
МКО-задача 2; число «разгонных» точек ![]() ; 10-я итерация
; 10-я итерация
На рис.7 представлена структура полученной нейро-нечеткой сети ANFIS.
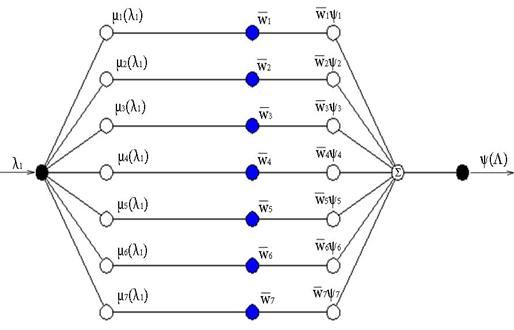
Рис.7. Структура нейро-нечеткой сети ANFIS
4.3 Задача 3 (МКО-задача 3). Критериальное множество МКО-задачи 3 представлено на рис. 8.
При ![]() «разгонных» точках решение задачи потребовало девять итераций (в исследовании [7] решение этой же задачи потребовало 14 итераций). Процесс решения задачи иллюстрирует таблица 3. Вид функции
«разгонных» точках решение задачи потребовало девять итераций (в исследовании [7] решение этой же задачи потребовало 14 итераций). Процесс решения задачи иллюстрирует таблица 3. Вид функции ![]() после 13 итераций представляет рис. 9 (напомним, что
после 13 итераций представляет рис. 9 (напомним, что ![]() ). На рис. 10 изображены линии уровня этой функции.
). На рис. 10 изображены линии уровня этой функции.
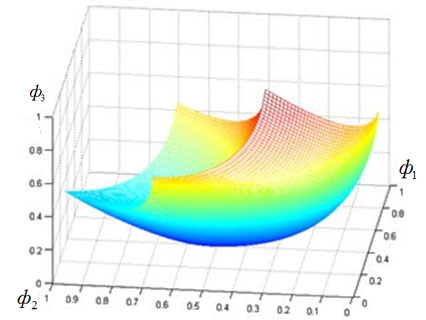
Рис. 8. Множество достижимости ![]() МКО-задачи 3
МКО-задачи 3
Таблица 3. Результаты решения МКО-задачи 3
|
|
|
|
|
|
|
|
|
|
|
1 | 0.14 | 0.45 | 0.36 | 0.16 | 0.19 | 6 | 2.11 | 0 | 0 | 0 |
2 | 0.35 | 0.27 | 0.20 | 0.26 | 0.19 | 8 | 2.08 | 0 | 0 | 0 |
3 | 0.21 | 0.46 | 0.31 | 0.14 | 0.23 | 8 | 2.10 | 0 | 0 | 0 |
4 | 0.22 | 0.58 | 0.32 | 0.08 | 0.35 | 7 | 2.04 | 14.75 | 23.26 | 0 |
5 | 0.19 | 0.80 | 0.43 | 0.02 | 0.56 | 3 | 2.20 | 7.47 | 16.67 | 0 |
6 | 0.23 | 0.47 | 0.29 | 0.13 | 0.26 | 8 | 2.03 | 11.69 | 21.32 | 0 |
7 | 0.37 | 0.27 | 0.19 | 0.26 | 0.21 | 8 | 2.00 | 15.28 | 24.88 | 0 |
8 | 0.36 | 0.25 | 0.20 | 0.27 | 0.19 | 7 | 2.11 | 19.06 | 28.79 | 0 |
9 | 0.35 | 0.31 | 0.21 | 0.23 | 0.22 | 9 | 2.04 | 11.79 | 22.32 | 0 |
10 | 0.34 | 0.33 | 0.21 | 0.22 | 0.23 | 9 | 2.13 | 14.41 | 26.01 | 0 |
11 | 0.22 | 0.47 | 0.30 | 0.14 | 0.25 | 8 | 2.14 | 12.45 | 24.10 | 0 |
12 | 0.34 | 0.32 | 0.21 | 0.22 | 0.22 | 9 | 2.12 | 17.88 | 29.52 | 0 |
13 | 0.33 | 0.31 | 0.22 | 0.23 | 0.21 | 9 | 2.08 | 19.42 | 31.03 | 0 |
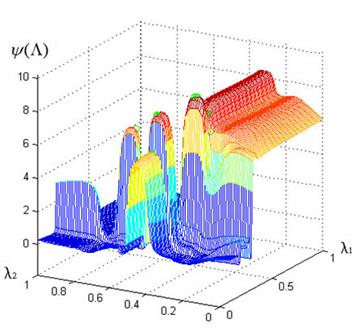
Рис. 9. Функция предпочтений ЛПР ![]() :
:
МКО-задача 3; число «разгонных» точек ![]() ; 13-я итерация
; 13-я итерация
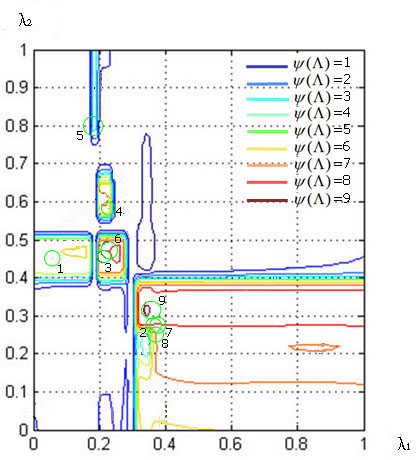
Рис. 10. Линии уровня функции предпочтений ЛПР ![]() :
:
МКО-задача 3; число «разгонных» точек ![]() ; 13-я итерация
; 13-я итерация
На рис. 11 изображена структура полученной нейро-нечеткой сети ANFIS.
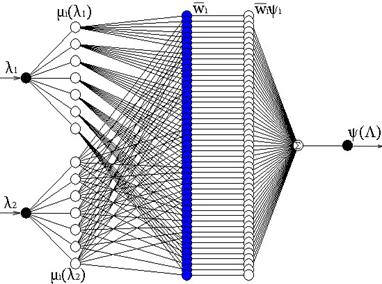
Рис.11. Структура нейро-нечеткой сети ANFIS
На рис. 12 показана зависимость времени выполнения одной итерации алгоритма от номера итерации. Из рисунка видно, что время выполнения итерации слабо зависит от ее номера. Здесь левая шкала относится к МКО-задаче 3, правая шкала – к МКО-задаче 1 и МКО-задаче 2.
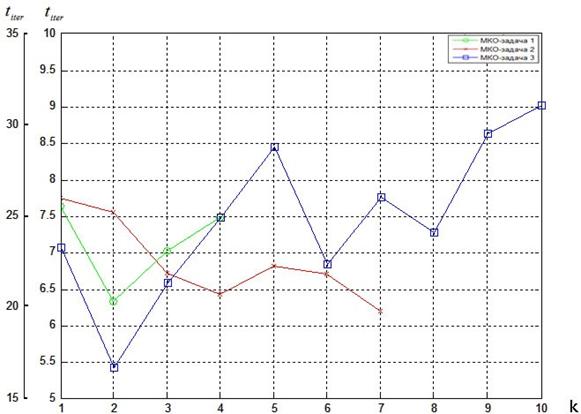
Рис. 12. Время выполнения одной итерации ![]() как функция номера итерации k
как функция номера итерации k
Заключение
Разработан прямой адаптивный метод решения МКО-задачи, основанный на аппроксимации функции предпочтений ЛПР с помощью аппарата нейро-нечеткого вывода. Выполнено исследование эффективности метода, показавшее перспективность его развития. Метод реализован в виде MatLab программы PREF-ANFIS.
Результаты исследования показывают, что для всех трех рассмотренных МКО-задач аппроксимация функции предпочтений ЛПР с помощью нечеткой логики позволяет найти решение задачи не более чем за 10 итераций. По сравнению с методом на основе нечеткой аппроксимации функции предпочтений ЛПР, рассмотренным в работе [7], данный метод позволяет получить решение МКО-задачи за меньшее число итераций. Это можно объяснить следующим образом. Теорема Ванга, являющаяся теоретической основой аппроксимации функций с помощью аппарата нечетких множеств, не накладывает никаких ограничений на параметры функций принадлежности переменных. В то же время в методе, рассмотренном в исследовании [7], такие ограничения наложены, что, естественно, сказывается на качестве аппроксимации. Таким образом, нейро-нечеткий вывод предоставляет собой более гибкий механизм для аппроксимации функции предпочтений. Другим достоинством данного метода является то, что время, необходимое для выполнения итерации в этом случае меньше по сравнению со временем, которое требуется для решения МКО-задач методом, предложенным в работе [7].
Литература
1. Лотов А.В. Введение в экономико-математическое моделирование / А.В. Лотов.-М.: Наука, 1984.-392 с.
2. Карпенко А.П. Один класс прямых адаптивных методов многокритериальной оптимизации / А.П. Карпенко, В.Г. Федорук // Информационные технологии.- 2009.- ╧5.- С.24-30.
3. Карпенко А.П. Нейросетевая аппроксимация функции предпочтений лица, принимающего решения, в задаче многокритериальной оптимизации / А.П. Карпенко, Д.Т. Мухлисуллина, В.А. Овчинниокв // Информационные технологии.- 2010 (в печати).
4. Мухлисуллина Д.Т. Исследование погрешности нейросетевой аппроксимации функции предпочтений лица, принимающего решения. [Электронный ресурс] / Д.Т. Мухлисуллина // Электронное научно-техническое издание: наука и образование. – 2009.- ╧12.(http://technomag.edu.ru).
5. Круглов В.В. Искусственные нейронные сети. Теория и практика / В.В. Круглов, В.В. Борисов.- М.: Горячая линия – Телеком, 2002. – 382 с.
6. Черноруцкий И.Г. Методы принятия решений / И.Г. Черноруцкий. – СПб.: БХВ-Петербург, 2005.-416 с.
7. Карпенко А.П. Многокритериальная оптимизация на основе нечеткой аппроксимации функции предпочтений лица, принимающего решения / А.П. Карпенко, Д.А. Моор, Д.Т. Мухлисуллина // Электронное научно-техническое издание: наука и образование.-2010.- ╧1 (http://technomag.edu.ru/doc/135375.html).
8. Лобарева И.Ф. Многоцелевая оптимизация формы лопасти гидротурбины / И.Ф. Лобарева, С.Г. Черный, Д.В. Чирков, В.А. Скороспелов, П.А. Турук // Вычислительные технологии, Том 11, ╧5, 2006. С.63 – 76.
9. Леоненков А. Нечеткое моделирование в среде MATLAB и FuzzyTECH / А. Леоненков.- СПб.: БВХ-Петербург, 2005.- 736 с.
10. Штовба С.Д. Введение в теорию нечетких множеств и нечеткую логику / С.Д. Штовба.- Режим доступа: http//www.matlab.exponenta.ru, свободный.
11. Штойер Р. Многокритериальная оптимизация. Теория, вычисления и приложения / Р. Штойер.– М.: Радио и связь, 1992.- 504 с.
Публикации с ключевыми словами: многокритериальная оптимизация, ANFIS
Публикации со словами: многокритериальная оптимизация, ANFIS
Смотри также:
- Исследование погрешности аппроксимации многомерной функции с помощью нейронных сетей с радиальными базисными функциями
- Информационная модель и основные функции программной системы многокритериальной оптимизации ╚Парето╩
- Разработка модуля однокритериальной оптимизации для системы многокритериальной оптимизации ╚Парето╩
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



