научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 04, апрель 2010
УДК 629.3.02
МГТУ имени Н.Э. Баумана.
E-mail sarach@yandex.ru
Важнейшей характеристикой, определяющей эффективность быстроходной гусеничной машины (БГМ), как и любого другого транспортного средства, является скорость движения, которая оказывает значительное влияние на динамические нагрузки силовой цепи машины при заданных дорожно-грунтовых условиях.
Скорость движения БГМ зависит от ее технических характеристик, внешних условий движения и квалификации водителя. Водитель в каждый момент времени стремится управлять машиной так, чтобы добиться максимальной скорости в данных условиях движения. Однако, несмотря на важную роль опыта водителя, в каждом конкретном случае существует верхняя не зависящая от водителя граница скорости, которая определяется техническими возможностями машины и внешними условиями движения. Эту скорость, являющуюся реальной скоростью машины в данных условиях при идеальном безошибочном управлении водителем, называют технической скоростью движения машины [1].
Техническая средняя скорость движения в каждых конкретных условиях дает возможность оценить потенциальные скоростные способности машины в данных условиях, а следовательно, и ее техническое совершенство как транспортного средства.
Средняя скорость движения БГМ по трассе определяется по формуле:
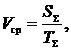
где SS – суммарный путь, пройденный машиной; TS – общее время, затраченное на движение по трассе, которое является суммой отрезков времени ti движения машины со скоростью Vi. Если принять, что Si – путь, пройденный машиной со скоростью Vi, тогда выражение для средней скорости примет вид:
 .
.
Разделим числитель и знаменатель полученного выражения на SS, и учитывая, что Si / SS = psi(V) – вероятность движения со скоростью Vi по пути, запишем:
 .
.
Переходя к непрерывным функциям через интегральную сумму в окрестности Vi, получим
psi(V) = dФs(V) = js(V) dv,
где Фs(V) – функция распределения скорости по пути, js(V) – плотность распределения скорости по пути.
Переходя от суммы к интегралу с пределами от 0 до Vmax, выражение для средней технической скорости примет вид:
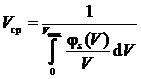 . (1)
. (1)
Как показывает опыт эксплуатации БГМ, их скорости при прямолинейном движении по неровностям в основном ограничиваются качеством системы подрессоривания. При плохой системе подрессоривания, вследствие жестких ударов балансиров катков в упоры, возникают вертикальные ускорения (более 3,5g [2]), заставляющие водителя снижать скорость. При отсутствии таких ударов, называющихся «пробоями» подвески, вертикальные ускорения обычно находятся в допустимых пределах. Поэтому основной характеристикой, оценивающей систему подрессоривания по влиянию на среднюю скорость БГМ, должна быть зависимость, отражающая возможность движения машины без «пробоев» подвески.
В качестве такой характеристики принимают скоростную характеристику системы подрессоривания – кривую, отражающую зависимость от скорости максимальной высоты неровностей, которые БГМ может преодолевать без «пробоев» подвески при самых неблагоприятных условиях движения по неровностям с гармоническим профилем [2]. Форма и, главным образом, высота расположения скоростной характеристики в координатах h и V определяет степень влияния системы подрессоривания на среднюю скорость БГМ. Иными словами, чем больше высота неровностей, которые БГМ преодолевает без «пробоев» во всем диапазоне скоростей, тем меньше система подрессоривания влияет на снижение средней скорости.
Покажем связь между средней скоростью движения БГМ и высотой «проходной» периодической неровности – высота периодических неровностей, которые БГМ может преодолевать без «пробоев» подвески или по ограничению предельных ускорений на месте водителя во всем скоростном диапазоне движения. Для этого представим скоростную характеристику системы подрессоривания БГМ в упрощенном виде (рис. 1), как это рекомендуется в [2]. Здесь на участке V £ V0 скоростная характеристика бесконечно возрастает, так как на низких скоростях (менее 10 км/ч) быстроходность гусеничной машины не ограничивается системой подрессоривания, а определяется только тягово-сцепными свойствами. На участке V0 £ V £ Vmax скоростная характеристика параллельна оси абсцисс и находится на высоте «проходной» периодической неровности h1 минимальной на всем скоростном диапазоне. Если реальная скоростная характеристика будет располагаться выше упрощенной, то влияние реальной системы подрессоривания на среднюю скорость БГМ будет меньше, чем влияние системы подрессоривания с упрощенной скоростной характеристикой.
При принятой скоростной характеристике функция быстроходности БГМ по системе подрессоривания имеет вид, показанный на рис. 2 [2], где Фs(h1) – вероятность встречи неровностей, высотой менее или равной h1. Например, на рис. 3 представлена функция распределения высот неровностей по пути для грунтовых дорог наезженных БГМ в средней полосе Европейской части России [2].
Известно, что функция быстроходности (вероятность того, что скорость движения будет больше заданной) при прямолинейном движении БГМ по неровностям, вследствие предположения о независимости ограничений скорости движения по плавности хода и по тяговым свойствам, определяется следующим образом [1]:
Fs(V) = Fsп(V)×Fsт(V),
где Fsп(V) – функция быстроходности по системе подрессоривания, Fsт(V) – функция быстроходности по тяговым свойствам.
Так как Fsп(V) = 1 – Фs(V) и dFs(V)/dv = – dФs(V)/dv = – js(V) [1], плотность распределения скорости по пути будет:
js(V) = jsп(V)×Fsт(V) + jsт(V)×Fsп(V).

Рис. 1. Упрощенная скоростная характеристика
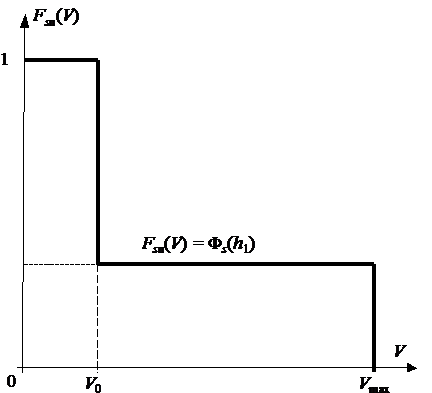
Рис. 2. Функция быстроходности по системе подрессоривания, соответствующая упрощенной скоростной характеристике рис. 1.

Рис. 3 Функции распределения вероятностей высоты неровностей по пути. 1 – трассы гусеничных машин; 2 – грунтовые дороги
Опуская промежуточные выкладки, в итоге получим выражение для средней технической скорости движения БГМ по неровностям [2]:
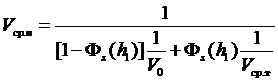 , (2)
, (2)
В [2] авторы называют эту скорость – средней скоростью, вычисленной с учетом ограничений по системе подрессоривания, и вводят безразмерный коэффициент качества системы подрессоривания

Вычисленная таким образом, средняя скорость по системе подрессоривания не может быть больше средней скорости по тяговым свойствам. В случае, если даже БГМ будет преодолевать все неровности без ограничения по плавности хода, то Фs(h1)=1, Kп=1. То есть для машин со «слабыми» тяговыми свойствами, посредственная система подрессоривания позволит получить высокий Kп. В то же время для энергооснащенных машин добиться высоких Kп практически невозможно.
Используемое понятие коэффициента качества системы подрессоривания не позволяет сравнивать технический уровень подвесок для машин с разной удельной мощностью. Вычисленная по формуле (2) Vср.п фактически является средней скоростью прямолинейного движения БГМ, то есть как с учетом тяговых свойств, так и ограничений по плавности хода и не подходит для определения направлений модернизации БГМ.
Если принять, что Vср.п – средняя скорость, определяемая только ограничениями по системе подрессоривания, то есть при отсутствии тяговых ограничений, в (2) надо вместо Vср.т подставить Vmax – максимальную скорость движения машины. Тогда выражение для Vср.п примет вид:
 (3)
(3)
Теперь коэффициент качества системы подрессоривания, для машин со «слабым» двигателем и «хорошей» подвеской, будет принимать значения более единицы. Полное соответствие между тяговыми свойствами и качеством системы подрессоривания достигается при Kп=1. Такая трактовка Kп позволяет определить пути модернизации БГМ.
Реальная скоростная характеристика системы подрессоривания существенно отличается от аппроксимированной ступенчатой характеристики и имеет явно выраженный участок плавного возрастания. Представим упрощенную скоростную характеристику в виде, показанном на рис. 4. Здесь на участке V £ V0 скоростная характеристика также бесконечно возрастает. На участке V0 £ V £ V1 реальная скоростная характеристика заменяется гиперболой с асимптотами V = V0 и h = h1. На участке V1 £ V £ Vmax скоростная характеристика параллельна оси абсцисс и находится на высоте «проходной» периодической неровности h1. Такая скоростная характеристика, в отличие от характеристики, представленной на рис. 1, позволяет учесть скорости движения, попадающие в заштрихованную область (рис. 4). Это представление позволяет получить более достоверную оценку средней скорости при ограничениях режимов движения по системе подрессоривания, что особо важно при определении нагруженности и долговечности элементов подвески БГМ.

Рис. 4. Предлагаемая упрощенная скоростная характеристика

Рис. 5 Новый вид функции распределения вероятностей высоты неровностей по пути
Для дальнейшего вывода формул и получения аналитического выражения, удобного для практического использования, необходимо сделать следующее допущение. Функция распределения высот неровностей по пути, представленная на рисунке 3, на участке h1 £ h £ h0 заменяется прямой линией. Новый вид функции распределения высот неровностей по пути представлен на рисунке 5.
Функцию быстроходности гусеничной машины по системе подрессоривания для новой скоростной характеристики и функции распределения высот неровностей по пути, определяем по известной методике [1, 2]. В прямоугольной системе координат (рис 6), в первом квадрате строится скоростная характеристика системы подрессоривания машины h=h(V), а во втором квадрате – функция распределения вероятностей высот неровностей по пути Фs(h1). Тогда функция быстроходности Fs(V) графически строится в четвертом квадрате выбранной системы координат. Ее окончательный вид, показан на рис. 7. Здесь при V £ V0 и V ³ V1 плотность распределения скорости по пути jsп(V) = |dFs(V)/dv| = 0.

Рис. 6. Определение функция быстроходности по системе подрессоривания БГМ
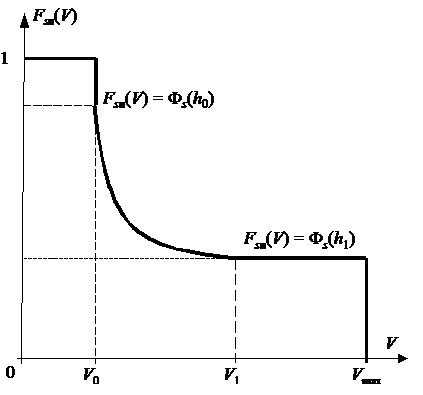
Рис. 7. Функция быстроходности по системе подрессоривания, соответствующая скоростной характеристике рис. 4 и функции распределения по пути высоты неровностей рис. 5
Интеграл из выражения (1) представим в виде суммы трех интегралов:
 .
.
Первый интеграл соответствует условиям движения со скоростями, не превышающими V0 по неровностям с максимальной высотой для решения задач плавности хода однозвенных БГМ h0 » 0,4м. Тогда вероятность того, что высота встречающиеся неровности будет больше чем h0, составит 1–Фs(h0).
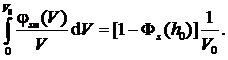 (4)
(4)
Третий интеграл соответствует условиям движения со скоростью Vmax по неровностям высотой менее h1. Он примет вид:
 (5)
(5)
Получим выражение для плотности распределения скорости по пути при ограничениях по системе подрессоривания на интервале скоростей
[V0; V1].
Используя гиперболический участок скоростной характеристики (рис. 4) можно записать
hi×Vi = const или h0×V0 = h1×V1.
То есть, если заданы три значения, например h1, V1 и h0, то всегда можно определить четвертое V0 = h1×V1 / h0.
Запишем выражение для функции быстроходности по системе подрессоривания в диапазоне скоростей V0 £ V £ V1, используя линейный участок функции распределения высот неровностей по пути (рис. 5).
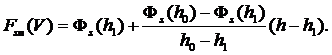
Опуская промежуточные преобразования, получим выражение для искомого интеграла:
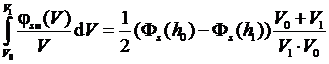 (6)
(6)
Используя (4), (5) и (6) запишем формулу для средней скорости по системе подрессоривания со скоростной характеристикой, представленной на рис. 4.
 (7)
(7)
По формуле (7) получим значения средних скоростей для различных БГМ, и сравним их со скоростями, вычисленными по формулам (2) и (3) и с данными эксперимента. При этом обозначим скорости вычисленные по формулам (2), (3) и (7) Vср.п1, Vср.п2 и Vср.п3 соответственно. По этим скоростям определим коэффициенты качества системы подрессоривания, показывающие влияние системы подрессоривания на возможную по тяговым свойствам среднюю скорость БГМ [2]:
Kп1 = Vср.п1/ Vср.т, Kп2 = Vср.п2/ Vср.т, Kп3 = Vср.п3/ Vср.т.
При расчете используем следующие исходные данные:
V0 – скорость БГМ (около 10 км/ч) по достижению которой необходимо начинать учитывать ограничения по системе подресоривания. До этой скорости, скорость БГМ определяется только тягово-сцепными свойствами. V0 рекомендуется определять по формуле V0 = h1×V1 / h0.
V1 – скорость БГМ на которой скоростная характеристика подвески имеет минимум: обычно соответствует резонансу по продольно-угловым или вертикальным колебаниям корпуса БГМ.
Vmax – максимальная скорость движения БГМ. Определяется из тактико-технических характеристик БГМ.
Vср.т – средняя техническая скорость по тяговым свойствам БГМ. Определяется по формуле: Vср.т = Nуг / f0 [1], где Nуг – удельная мощность БГМ, реализуемая на грунте; Nуг = (Nдв – DNвн) / G0; Nдв – мощность, развиваемая двигателем; DNвн – внутренние потери мощности в БГМ (при расчетах примем DNвн = 0,1 Nдв); G0 – вес БГМ; f0 – суммарный коэффициент сопротивления движению. Среднее значение суммарного коэффициента сопротивления движению для бездорожья составляет 0,12 [1].
h0 – максимальная высота периодических неровностей, учитывающихся при решении задач плавности хода однозвенных БГМ (h0 » 0,4м).
h1 – максимальная высота периодических неровностей, которые БГМ способна преодолевать во всем скоростном диапазоне. Соответствует минимуму скоростной характеристики подвески.
Фs(h0), Фs(h1) – вероятности встречи неровностей, высотой менее или равной h0 и h1 соответственно. Определяются функцией распределения вероятностей высот неровностей по пути (рис. 3) Для h0 = 0,4м Фs(h0) = 0,97.
Результаты расчетов занесены в таблицу.
Анализируя полученные результаты можно сделать вывод, что средние скорости при ограничениях режимов движения по системе подрессоривания, рассчитанные по формулам (3) и (7):
- более согласуются с результатами экспериментальных данных (средние скорости движения БГМ 1, БГМ 2 и БГМ 3 на маршах при контрольных испытаниях в средней полосе европейской части СССР составляют 29, 33 и 36 км/ч соответственно);
- в среднем на 10% и на 23% выше, средних скоростей, вычисленных по формуле (2).
Таким образом, использование уточненных формул позволяет получить более достоверную оценку средней скорости БГМ при ограничениях режимов движения по системе подрессоривания, что особо важно при определении нагруженности и долговечности элементов подвески БГМ. В тоже время использование формулы (2) дает гарантированный результат при оценке скорости прямолинейного движения на этапе проектирования.
Кроме того, значения коэффициентов качества системы подрессоривания для скоростей, вычисленных по формулам (3) и (7), позволяют судить о том, дает ли прирост средней скорости прямолинейного движения увеличение мощности двигателя. Если Kп < 1, то увеличивать мощность двигателя смысла не имеет, если Kп > 1 – увеличение мощности двигателя позволит повысить Vср при той же системе подрессоривания.
Таблица
Характеристики БГМ
|
|
m, т |
Nдв, кВт |
Vmax, км/ч |
Nуг, кВт/т |
Vср.т, км/ч |
h1, м |
Фs(h1) |
|
БГМ 1 |
42,4 |
515 |
60 |
12,15 |
33,4 |
0,15 |
0,65 |
|
БГМ 2 |
44,5 |
618 |
60 |
13,89 |
38,2 |
0,16 |
0,7 |
|
БГМ 3 |
46 |
919 |
70 |
19,98 |
55,0 |
0,17 |
0,75 |
Продолжение таблицы
|
V1, км/ч |
V0, км/ч |
Vср.п1, км/ч |
Kп1 |
Vср.п2, км/ч |
Kп2 |
Vср.п3, км/ч |
Kп3 |
|
25,9 |
9,72 |
18,0 |
0,54 |
21,3 |
0,63 |
0,75 |
0,64 |
|
32,4 |
13,0 |
24,1 |
0,63 |
28,7 |
41,2 |
35,0 |
27,4 |
|
32,4 |
13,8 |
31,4 |
0,57 |
34,6 |
0,75 |
0,92 |
0,82 |
Список литературы
1. Савочкин В.А., Дмитриев А.А. Статистическая динамика транспортных и тяговых гусеничных машин – М.: Машиностроение, 1993. – 320с.
2. Дмитриев А. А., Чобиток В. А., Тельминов А. В. Теория и расчет нелинейных систем подрессоривания гусеничных машин. – М.: Машиностроение, 1976. – 207 с.
Публикации с ключевыми словами: гусеничная машина, Коэффициент качества системы подрессоривания
Публикации со словами: гусеничная машина, Коэффициент качества системы подрессоривания
Смотри также:
- Оценка эффективности метода повышения быстроходности двухзвенной гусеничной машины, использующего управление углом складывания секций в вертикальной плоскости во время движения
- 77-30569/216198 Особенности моделирования электрической трансмиссии транспортного средства на примере линейного тягового электрического привода
- 77-30569/245694 Математическая модель гусеничного обвода
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



