научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 04, апрель 2010
МГТУ им. Н.Э. Баумана
Введение
В настоящее время при решении задач оптимизации все более широкое распространение получают стохастические поведенческие методы [1]. Одним из таких методов является метод роя частиц (Particle Swarm Optimization, PSO), основанный на закономерностях социального поведения [2-3]. Первоначальной целью исследований в области роя частиц было обнаружение базовых принципов, благодаря которым стая рыб или птиц синхронно меняет направление движения. К настоящему времени концепция роя частиц развилась в простой и перспективный оптимизационный многоагентный метод.
В методе PSO агентами являются частицы в пространстве параметров задачи оптимизации. В каждый момент времени (на каждой итерации) частицы имеют в этом пространстве некоторое положение и вектор скорости. Для каждого положения частицы вычисляется соответствующее значение целевой функции, и на этой основе по определенным правилам частица меняет свое положение и скорость в пространстве поиска [3].
Достаточно новым является применение метода PSO в задаче многокритериальной оптимизации (Multi-Objective Swarm Optimization, MOPSO) [1]. В работе рассматривается применение этого метода для приближенного построения множества Парето в указанной задаче.
1. Постановка задачи
Совокупность частных критериев оптимальности ![]() образует векторный критерием оптимальности
образует векторный критерием оптимальности ![]() , где
, где ![]() - вектор варьируемых параметров. Положим, что ставится задача минимизации каждого из частных критериев в одной и той же области допустимых значений
- вектор варьируемых параметров. Положим, что ставится задача минимизации каждого из частных критериев в одной и той же области допустимых значений ![]() . Запишем задачу многокритериальной оптимизации в виде
. Запишем задачу многокритериальной оптимизации в виде
![]() . (1)
. (1)
Положим, что частные критерии оптимальности нормализованы с использованием, например, относительных отклонений частных критериев от их минимальных значений:
![]() ,
,
где ![]() ,
, ![]() . Сохраним за нормализованными критериями прежние обозначения.
. Сохраним за нормализованными критериями прежние обозначения.
Введем понятие пространства критериев ![]() . Пространство критериев имеет размерность
. Пространство критериев имеет размерность ![]() (по числу частных критериев) и образуется
(по числу частных критериев) и образуется ![]() ортогональными осями координат, вдоль которых откладываются значения частных критериев оптимальности
ортогональными осями координат, вдоль которых откладываются значения частных критериев оптимальности ![]() .
.
Векторный критерий оптимальности ![]() выполняет отображение множества допустимых значений
выполняет отображение множества допустимых значений ![]() в некоторую область
в некоторую область ![]() , где
, где ![]() — пространство варьируемых параметров.
— пространство варьируемых параметров.
Введем на множестве ![]() отношение предпочтения
отношение предпочтения ![]() . Будем говорить, что вектор
. Будем говорить, что вектор ![]() предпочтительнее вектора
предпочтительнее вектора ![]() , и писать
, и писать ![]() , если среди равенств и неравенств
, если среди равенств и неравенств ![]() имеется хотя бы одно строгое неравенство [4].
имеется хотя бы одно строгое неравенство [4].
Аналогично, на множестве ![]() введем отношение доминирования: будем говорить, что векторный критерий оптимальности
введем отношение доминирования: будем говорить, что векторный критерий оптимальности ![]() доминирует векторный критерий оптимальности
доминирует векторный критерий оптимальности ![]() , и писать
, и писать ![]() , если
, если ![]() [4].
[4].
Выделим из множества ![]() подмножество
подмножество ![]() точек, для которых нет точек, их доминирующих. Это множество называется фронтом Парето (рис. 1). Множество
точек, для которых нет точек, их доминирующих. Это множество называется фронтом Парето (рис. 1). Множество ![]() , соответствующее множеству
, соответствующее множеству ![]() , называется множеством Парето (переговорным множеством, областью компромисса). Поскольку множество
, называется множеством Парето (переговорным множеством, областью компромисса). Поскольку множество ![]() на рисунке 1 является выпуклым, то множество
на рисунке 1 является выпуклым, то множество ![]() в данном случае представляет собой дугу AB, в которой точка A соответствует
в данном случае представляет собой дугу AB, в которой точка A соответствует ![]() , а точка B —
, а точка B — ![]() . Среди точек
. Среди точек ![]() нет доминируемых, поскольку
нет доминируемых, поскольку ![]() , но
, но ![]() .
.

Рис. 1. К определению фронта Парето (![]() )
)
Ставится задача приближенного построения множества Парето (а, тем самым, и фронта Парето) в задаче многокритериальной оптимизации (1).
2. Канонический метод роя частиц (PSO)
Множество частиц обозначим ![]() , где
, где ![]() – количество частиц в рое (размер популяции). В дискретный момент времени
– количество частиц в рое (размер популяции). В дискретный момент времени ![]() координаты частицы
координаты частицы ![]() определяются вектором
определяются вектором ![]() , а ее скорость - вектором
, а ее скорость - вектором ![]() . Множество частиц в дискретный момент времени обозначим
. Множество частиц в дискретный момент времени обозначим ![]() ;
; ![]() - количество итераций. Начальные координаты и скорости частицы
- количество итераций. Начальные координаты и скорости частицы ![]() равны
равны ![]() ,
, ![]() соответственно, где
соответственно, где ![]() - матрица случайных чисел,
- матрица случайных чисел, ![]() - нулевая матрица.
- нулевая матрица.
Итерации в каноническом методе PSO выполняются по следующей схеме:
![]() ; (2)
; (2)
![]() . (3)
. (3)
Здесь ![]() представляет собой
представляет собой ![]() -мерный вектор псевдослучайных чисел, равномерно распределенных в интервале
-мерный вектор псевдослучайных чисел, равномерно распределенных в интервале ![]() ;
; ![]() - символ покомпонентного умножения векторов;
- символ покомпонентного умножения векторов; ![]() - вектор координат частицы
- вектор координат частицы ![]() с наилучшим значением целевой функции
с наилучшим значением целевой функции ![]() за все время поиска
за все время поиска ![]() ;
; ![]() - вектор координат соседней с данной частицы с наилучшим за время поиска
- вектор координат соседней с данной частицы с наилучшим за время поиска ![]() значением целевой функции
значением целевой функции ![]() ;
; ![]() - свободные параметры алгоритма. Важнейшее в методе PSO понятие соседства частиц зависит от используемой топологии соседства и определено, например, в работе [2].
- свободные параметры алгоритма. Важнейшее в методе PSO понятие соседства частиц зависит от используемой топологии соседства и определено, например, в работе [2].
Пересчет координат частиц по формулам (2), (3) может происходить по синхронной схеме (обновление координат частиц выполняется только после определения текущих скоростей всех ![]() частиц) или по асинхронной схеме (расчет новых координат части производится до завершения указанных вычислений).
частиц) или по асинхронной схеме (расчет новых координат части производится до завершения указанных вычислений).
В процессе итераций вектор ![]() образует так называемый собственный путь (private guide) частицы
образует так называемый собственный путь (private guide) частицы ![]() , а вектор
, а вектор ![]() - локальный путь (local guide) этой частицы.
- локальный путь (local guide) этой частицы.
Свободный параметр ![]() определяет «инерционные» свойства частиц (при
определяет «инерционные» свойства частиц (при ![]() движение частиц замедляется). Рекомендуемое значение параметра
движение частиц замедляется). Рекомендуемое значение параметра ![]() равно 0,7298 [2]. В процессе оптимизации может быть эффективным постепенное уменьшение коэффициента
равно 0,7298 [2]. В процессе оптимизации может быть эффективным постепенное уменьшение коэффициента ![]() от 0.9 до 0.4. При этом большие значения параметра обеспечивают широкий обзор пространства поиска, а малые – точную локализацию минимума целевой функции. Рекомендуемые значения свободных параметров
от 0.9 до 0.4. При этом большие значения параметра обеспечивают широкий обзор пространства поиска, а малые – точную локализацию минимума целевой функции. Рекомендуемые значения свободных параметров ![]() равны 1,49618 [2].
равны 1,49618 [2].
Второй компонент в формуле (2) называется «когнитивным» компонентом (по социальной аналогии) и формализует тенденцию частицы вернуться в положение с минимальным значением целевой функции. Третий компонент в формуле (2) называется «социальным» компонентом. Компонент отражает влияние на данную частицу ее соседей.
3. Метод многокритериальной оптимизации роем частиц (MOPSO)
Важной частью метода MOPSO является определение глобально лучшей частицы (в смысле формулы (1)) для каждой частицы в популяции. В многокритериальной задаче глобально лучшую частицу следует искать на множестве Парето. С этой целью в методе MOPSO используется архив частиц ![]() . В нем хранятся координаты недоминируемых частиц
. В нем хранятся координаты недоминируемых частиц ![]() . Схема метода MOPSO представлена на рисунке 2.
. Схема метода MOPSO представлена на рисунке 2.
Шаг 1: t=0
Шаг 2 (инициализация):
Инициализация популяции ![]() :
:
For i=1 to ![]()
![]() ;
; ![]() ;
; ![]() =
= ![]()
End;
Инициализация архива частиц:
![]() ;
;
Шаг 3: Обновление архива частиц: ![]() ;
;
Шаг 4:
For i=1 to ![]()
Вычисление вектора глобально лучших частиц:
![]() ;
;
For j=1 to n
![]() ;
;
![]()
End;
If (![]() )
)
![]()
End;
End;
Шаг 6 (проверка критерия останова итераций):
t=t+1;
IF t![]() T
T
go to шаг 3;
End
Рис. 2. Схема алгоритма MOPSO
В результате работы алгоритма MOPSO на итерации ![]() происходит обновление архива
происходит обновление архива ![]() . Функция Update выполняет сравнение координат частиц из архива
. Функция Update выполняет сравнение координат частиц из архива ![]() с координатами частиц, полученными на текущей итерации t. Если некоторая частица текущего поколения
с координатами частиц, полученными на текущей итерации t. Если некоторая частица текущего поколения ![]() доминирует частицу
доминирует частицу ![]() из архива, то координаты частицы
из архива, то координаты частицы ![]() заменяя.т в архиве координаты частицы
заменяя.т в архиве координаты частицы ![]() . Если частица
. Если частица ![]() доминирует частицу
доминирует частицу ![]() , то частицу
, то частицу ![]() не добавляется в архив.
не добавляется в архив.
Заметим, что из приведенной схемы функции Update следует, что на первой итерации, когда архив пуст, функция Update добавляет в архив все частицы текущего поколения, которые не доминируют друг друга.
Выбор глобально лучшей частицы осуществляет функция FindGlobalBest. Существует несколько способов реализации этой функции. В данной работе используется метод «меняющихся» соседей» Хью и Эберхарта [5]. Рассмотрим суть этого метода на примере задачи двухкритериальной оптимизации. Поиск глобально лучшей частицы для каждой частицы популяции осуществляется в этом случае следующим образом: сначала вычисляем расстояние от частицы ![]() до других частиц архива
до других частиц архива ![]() , используя значения первого («фиксированного») критерия оптимальности
, используя значения первого («фиксированного») критерия оптимальности ![]() . Таким образом, для частицы
. Таким образом, для частицы ![]() находим k ее ближайших локальных соседей. Затем, используя второй критерий
находим k ее ближайших локальных соседей. Затем, используя второй критерий ![]() , находим наиболее оптимальную частицу из этих числа этих соседей частицы
, находим наиболее оптимальную частицу из этих числа этих соседей частицы ![]() . Это частица и принимается в качестве глобально лучшей частицы для частицы
. Это частица и принимается в качестве глобально лучшей частицы для частицы ![]() .
.
Итерации могут продолжаться до тех пор, пока множество недоминируемых решений не перестанет меняться, либо до достижения заданного числа итераций.
5. Исследование эффективности метода MOPSO
Исследование выполнено для следующей тестовой задачи:
· множество допустимых значений
![]() ; (4)
; (4)
· частные критерии оптимальности
 (5)
(5)
Известно, что множество ![]() для задачи (4), (5) имеет вид, представлены на рис. 3б, а множество Парето
для задачи (4), (5) имеет вид, представлены на рис. 3б, а множество Парето ![]() представляет собой отрезок прямой, соединяющий точки (0, 0), (1, 1) рис. 3а.
представляет собой отрезок прямой, соединяющий точки (0, 0), (1, 1) рис. 3а.

а) б)
Рис. 3. Точные множество Парето (а) и фронт Парето (б) для тестовой задачи
На основе большого количества экспериментов было установлено, что оптимальными для задачи (4), (5) являются следующие параметры метода MOPSO: размер популяции ![]() ; количество итераций
; количество итераций ![]() .
.
На рисунке 4 изображена аппроксимация множества Парето и соответствующая аппроксимация фронта Парето, полученные для задачи (4), (5) с помощью алгоритма MOPSO. Получение указанных результатов потребовало примерно 10 минут процессорного времени (расчеты производились на персональном компьютере с процессором 2,16 Гц и 2 ГБ опертивной памяти).
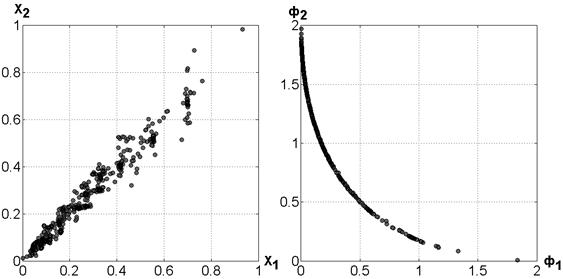
а) б)
Рис. 4. Аппроксимация множества Парето (а) и фронта Парето (б) для тестовой задачи
Необходимо отметить, что для вычислительно простых критериев оптимальности, решение задачи (1) полным перебором на достаточно точной сетке, покрывающей множество ![]() , требует затрат процессорного времени, сравнимых с указанным выше временем. Однако, при увеличении сложности критериев, метод MOPSO позволяет находить решение приемлемой точности за существенно меньшее время.
, требует затрат процессорного времени, сравнимых с указанным выше временем. Однако, при увеличении сложности критериев, метод MOPSO позволяет находить решение приемлемой точности за существенно меньшее время.
Поскольку известно точное решение тестовой задачи (4), (5), имеется возможность количественно оценить качество полученной аппроксимации множества Парето. Для этого было вычислено среднее отклонение частицы от идеального множества (отрезка прямой с концами в точках (0,0), (1,1), см. Рис.3а). На рисунке 5 приведены полученные результаты.
Сплошной линией на рисунке 5 показано среднее отклонение от точного решения (M), как функция числа итераций (t). Рисунок показывает, что метод сходится уже на первых 100-200 итерациях, после чего имеет место стагнация итерационного процесса.
Пунктиром на рисунке 5 показана величина среднего отклонения (σ) частиц от точного решения. Величина (σ) в некоторой степени демонстрирует то факт, что в архивном множестве ![]() нет частиц, которые расположены суперблизко и супердалеко от точного решения.
нет частиц, которые расположены суперблизко и супердалеко от точного решения.

Рис. 5. Оценка качества аппроксимации
Дополнительно было выполнено исследование производительности алгоритма. Для этого было выявлено, каким образом с течением итераций растет размер архива ![]() и как этот размер влияет на общее время решения задачи. Некоторые результаты экспериментов приведены на рисунке 6. На рисунке сплошная линия показывает размер архива
и как этот размер влияет на общее время решения задачи. Некоторые результаты экспериментов приведены на рисунке 6. На рисунке сплошная линия показывает размер архива ![]() в функции количества итераций (t), а пунктирная линия – время вычислений
в функции количества итераций (t), а пунктирная линия – время вычислений ![]() . Заметим, что в данном варианте алгоритма был использован архив
. Заметим, что в данном варианте алгоритма был использован архив ![]() , не имеющий ограничения на его размер. Это позволило накапливать в архиве
, не имеющий ограничения на его размер. Это позволило накапливать в архиве ![]() все Парето оптимальные точки. Для реальных задач многокритериальной оптимизации необходимо ограничивать размер архива, чтобы его неограниченный рост не привел к нехватке памяти компьютера.
все Парето оптимальные точки. Для реальных задач многокритериальной оптимизации необходимо ограничивать размер архива, чтобы его неограниченный рост не привел к нехватке памяти компьютера.
Заключение
Работа демонстрирует подход к приближенному построению множества Парето в задаче многокритериальной оптимизации с помощью метода MOPSO. Проведенное исследование показало, что данный метод, будучи относительно простым (как математически, так и в реализации), обеспечивает решение задачи с приемлемой точностью.

Рис. 6. Время вычислений τ и размер архива ![]() в функции количества итераций
в функции количества итераций ![]()
К недостаткам метода можно отнести то, что выбор глобально лучшей частицы сильно зависит от выбора «фиксированного» критерия [1]. Для преодоления этого недостатка планируется использовать модифицированные методы, приведенные, например, в статье [1]. В развитие работы планируется также реализация критерия останова метода, основанного на отсутствии роста размера архива в течение заданного количества итераций.
Авторы выражают благодарность Карпенко А.П. и Селиверстову Е.Ю. за плодотворные обсуждения постановки задачи и методов ее решения.
Литература
1. Mostaghim S., Teich, J. Strategies for Finding Good Local Guides in Multi-Objective Particle Swarm Optimization (MOPSO) // Swarm Intelligence Symposium: Proceeding, 2003. - pp. 26–33.
2. Карпенко А.П., Селиверстов Е.Ю. Глобальная оптимизация методом роя частиц. Обзор // Информационные технологии, 2010, ╧ 2, c. 25-34.
3. Субботин С.А., Олейник Ан.А., Олейник Ал.А. PSO-метод, «Интеллектуальные мультиагентные методы (Swarm Intelligence)», ╧3, 2006, с. 55-70.
4. Карпенко А.П. Методы оптимизации [Электронный ресурс].- (http://bigor.bmstu.ru).
5. Hu X., Eberhart R. Multiobjective optimization using dynamic neighborhood particle swarm optimization // World Congress on Computational Inelligence: Proceeding, 2002.- pp. 1677–1681.
Публикации с ключевыми словами: многокритериальная оптимизация, множество Парето, метод роя частиц, метод PSO
Публикации со словами: многокритериальная оптимизация, множество Парето, метод роя частиц, метод PSO
Смотри также:
- Эффективность оптимизации методом непрерывно взаимодействующей колонии муравьев (CIAC)
- Метод приближенного построения границы области достижимости многосекционного манипулятора типа ╚хобот╩
- Архитектура и программная реализация системы для оценки качества Парето-аппроксимации в задаче многокритериальной оптимизации
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



