научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 02, февраль 2010
УДК 536.75
Ташкентский Государственный педагогический университет
им. Низами, кафедра «методики преподавания физики»
tgpu_info@edu.uz
Введение
Принято считать, что теплопроводность сверхпроводников в области температур ![]() обусловлена релаксацией фононной подсистемы и носит в принципе такой же характер, что и в диэлектриках. Однако прекращение роста и следующее вслед за этим резкое уменьшение решеточной составляющей
обусловлена релаксацией фононной подсистемы и носит в принципе такой же характер, что и в диэлектриках. Однако прекращение роста и следующее вслед за этим резкое уменьшение решеточной составляющей ![]() однозначно указывают на существование дополнительного механизма рассеяния, роль которого может быть определяющей, начиная с
однозначно указывают на существование дополнительного механизма рассеяния, роль которого может быть определяющей, начиная с ![]() (рис. 1).
(рис. 1).

Таким механизмом, по-видимому, является резонансное рассеяние квазичастиц (обычных электронов). На фоне рассеяния фононов примесями, дефектами и границами образца резонансное рассеяние как бы «ускоряет» динамику падения![]() , внося тем самым определенный вклад в обеспечение стационарности режима падения (в том, что в области спада
, внося тем самым определенный вклад в обеспечение стационарности режима падения (в том, что в области спада ![]() могло накопиться необходимое для этого число квазичастиц можно объяснить, например, эффектом «увлечения обычных электронов фононами»).
могло накопиться необходимое для этого число квазичастиц можно объяснить, например, эффектом «увлечения обычных электронов фононами»).
Характерная длина волны квазичастицы![]() в актуальной области температур на несколько порядков превышает радиус действия поля примеси
в актуальной области температур на несколько порядков превышает радиус действия поля примеси ![]() (т.е.
(т.е. ![]() Å), что позволяет ограничиться
Å), что позволяет ограничиться ![]() волнами при исследовании влияния резонансного рассеяния на динамику спада
волнами при исследовании влияния резонансного рассеяния на динамику спада ![]() .
.
Минимальная длина когерентности ![]() на порядок превышает
на порядок превышает ![]() (где
(где ![]() эффективный радиус резонансного уровня
эффективный радиус резонансного уровня ![]() ), соответственно средняя вероятность резонансного рассеяния обычных электронов на порядок превышает вероятность их
), соответственно средняя вероятность резонансного рассеяния обычных электронов на порядок превышает вероятность их ![]() спаривания. В этом смысле можно сказать, что резонансное рассеяние как бы «блокирует»
спаривания. В этом смысле можно сказать, что резонансное рассеяние как бы «блокирует» ![]() спаривание квазичастиц, препятствуя их переходу в сверхпроводящее состояние. Величина щели
спаривание квазичастиц, препятствуя их переходу в сверхпроводящее состояние. Величина щели ![]() мэВ одного порядка с величиной
мэВ одного порядка с величиной ![]() в полупроводниках [2,3] (переход в сверхпроводящее состояние не влияет на состояние
в полупроводниках [2,3] (переход в сверхпроводящее состояние не влияет на состояние ![]() ), так что подавляющая часть квазичастиц вблизи пФ подвержена резонансному рассеянию при одновременном выполнении условий:
), так что подавляющая часть квазичастиц вблизи пФ подвержена резонансному рассеянию при одновременном выполнении условий:![]() и
и ![]() . В то же время, не исключена возможность положительной корреляции между резонансным рассеянием и сверхпроводимостью [4]. Резонансный уровень при этом играет роль центра захвата квазичастиц с последующим их
. В то же время, не исключена возможность положительной корреляции между резонансным рассеянием и сверхпроводимостью [4]. Резонансный уровень при этом играет роль центра захвата квазичастиц с последующим их ![]() спариванием. Легко, однако, показать, что вероятность такого процесса весьма мала. Отмеченная выше положительная корреляция имеет место только при концентрациях
спариванием. Легко, однако, показать, что вероятность такого процесса весьма мала. Отмеченная выше положительная корреляция имеет место только при концентрациях ![]() .
.
В предлагаемой работе на основе допущения о выполнении вышеуказанных условий в рамках изотропной модели БКШ рассматривается метод определения возможного резонансного уровня в сверхпроводящих образцах, содержащих небольшие концентрации примеси (![]() ). При этом, разумеется, исключается область температур, близких к абсолютному нулю, где число квазичастиц экспоненциально мало:
). При этом, разумеется, исключается область температур, близких к абсолютному нулю, где число квазичастиц экспоненциально мало: ![]() .
.
Методика расчета ![]()
Тепловой поток определяется соотношением
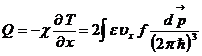 , (1)
, (1)
где ![]() возмущенная функция распределения квазичастиц, находящихся под действием температурного градиента и взаимодействующих с атомами примеси. Для ее нахождения запишем соответствующее кинетическое уравнение:
возмущенная функция распределения квазичастиц, находящихся под действием температурного градиента и взаимодействующих с атомами примеси. Для ее нахождения запишем соответствующее кинетическое уравнение:
![]() . (2)
. (2)
Здесь ![]() энергия квазичастицы,
энергия квазичастицы, ![]() энергия квазичастицы в нормальном металле, отсчитанная от пФ;
энергия квазичастицы в нормальном металле, отсчитанная от пФ; ![]() ,
,![]() время релаксации квазичастиц на примесях.
время релаксации квазичастиц на примесях.
С левой стороны вместо ![]() подставим равновесную функцию
подставим равновесную функцию ![]() . Тогда уравнение (2) приводится к виду
. Тогда уравнение (2) приводится к виду
![]() . (3)
. (3)
Нахождение ![]() осуществляется следующим образом. Запишем гамильтониан взаимодействия квазичастиц с атомами примеси в представлении вторичного квантования
осуществляется следующим образом. Запишем гамильтониан взаимодействия квазичастиц с атомами примеси в представлении вторичного квантования
![]() , (4)
, (4)
где ![]() и
и ![]() ферми-операторы рождения и уничтожения квазичастиц,
ферми-операторы рождения и уничтожения квазичастиц, ![]() матричный элемент плавной части
матричный элемент плавной части ![]() , который при слабых возбуждениях можно аппроксимировать формулой
, который при слабых возбуждениях можно аппроксимировать формулой
![]()
![]() , (5)
, (5)
где ![]() нормировочный объем,
нормировочный объем, ![]() ,
, ![]() квазиимпульс [5].
квазиимпульс [5].
Выполняя стандартное ![]() преобразование Боголюбова, гамильтониан (4) (с учетом (5)) можно привести к виду
преобразование Боголюбова, гамильтониан (4) (с учетом (5)) можно привести к виду
![]() , (6)
, (6)
описывающему сверхпроводящее состояние (![]() число квазичастиц).
число квазичастиц).
Далее с помощью формулы ![]() находим величину
находим величину ![]() :
:

![]() . (7)
. (7)
Подставляя полученное выражение для ![]() в уравнение (3), находим искомую функцию распределения
в уравнение (3), находим искомую функцию распределения ![]() , а затем вычисляем коэффициент теплопроводности
, а затем вычисляем коэффициент теплопроводности ![]() :
:
![]()
![]() ,
,
 ,
,  . (8)
. (8)
Сравнивая обе части (8) при общем множителе ![]() , получим
, получим

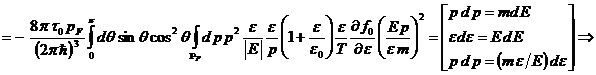
![]()
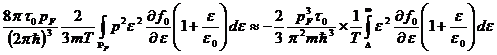 .
.
В результате имеем
![]() , (9)
, (9)

Если положить![]() , то отсюда следует квадратичный закон изменения величины
, то отсюда следует квадратичный закон изменения величины ![]() :
:
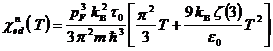 . (10)
. (10)
Наличие квадратичного члена в уравнении (9) с учетом знака ![]() приводит к тому, что функция
приводит к тому, что функция ![]() имеет максимум при
имеет максимум при ![]() . Подобные максимумы действительно наблюдаются для благородных металлов [6, стр.227].
. Подобные максимумы действительно наблюдаются для благородных металлов [6, стр.227].
В пределе при ![]() из (9) следует результат Бардина, Рикайзена и Тевордта соответствующий модели непроницаемых сфер:
из (9) следует результат Бардина, Рикайзена и Тевордта соответствующий модели непроницаемых сфер:
![]() .
.
Формула (9) в том виде, в котором она приведена выше, не вполне удобна для теоретических расчетов, поэтому целесообразно придать ей более компактную форму. С помощью формулы

и последующего суммирования рядов, функцию ![]() можно привести к виду
можно привести к виду
 . (11)
. (11)
Следовательно
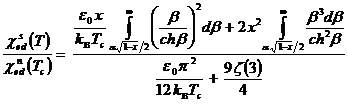 . (12)
. (12)
Здесь учтено, что ![]() ,
, ![]() ,
, ![]() . В итоге приходим к формуле
. В итоге приходим к формуле
 . (13)
. (13)
Пороговые значения проявления резонансного рассеяния для ниобия равны [1] ![]() ,
, ![]() (рис.1). Подставляя эти значения в формулу (13), получим
(рис.1). Подставляя эти значения в формулу (13), получим ![]() мэВ. Это значение
мэВ. Это значение ![]() по порядку величин согласуется с результатами измерения резонансного уровня в полупроводниках [2,3].
по порядку величин согласуется с результатами измерения резонансного уровня в полупроводниках [2,3].
Заключение
Основным результатом настоящей работы являются формулы (7), (10) и формула (13), позволяющие вычислить, соответственно, среднее время релаксации, значение резонансного уровня в благородных металлах и в сверхпроводниках.
Спад теплопроводности обусловлен не столько рассеянием фононов на границах и дефектах кристалла, сколько резонансным рассеянием обычных ![]() электронов (строго говоря, в принципе возможны и другие механизмы релаксации, однако мы акцентируем внимание именно на резонансном рассеянии).
электронов (строго говоря, в принципе возможны и другие механизмы релаксации, однако мы акцентируем внимание именно на резонансном рассеянии).
Наличие острого максимума на экспериментальной кривой теплопроводности однозначно указывает на появление резонансного рассеяния, специфика которого отражается ходом кривой: при незначительном понижении температуры наблюдается аномально высокий прирост теплового сопротивления
В актуальной области интегралы в (12) не очень чувствительны к функции ![]() , что позволяет получить нижнюю оценку
, что позволяет получить нижнюю оценку ![]() :
:
![]() .
.
Тогда для верхнего предела сечения рассеяния получим
![]() см²,
см²,
для среднего времени задержки -
![]() с.
с.
Полученное значение ![]() соответствует «shape»-резонансам в случае газовой фазы. Соответственно для аппроксиманты
соответствует «shape»-резонансам в случае газовой фазы. Соответственно для аппроксиманты ![]() (с учетом
(с учетом![]() и других возможных механизмов релаксации) имеем
и других возможных механизмов релаксации) имеем
![]() .
.
Таким образом, каждый последующий учет какого либо возможного механизма релаксации дает график, все ближе прилегающий к экспериментальной кривой, восстанавливая тем самым истинный ход спада![]() и подчеркивая при этом его резонансный характер в окрестности максимума.
и подчеркивая при этом его резонансный характер в окрестности максимума.
Предложенную методику расчета можно легко обобщить на случай сверхпроводящих низкоразмерных структур с квантовыми ямами на основе методики предложенной в работе [7].
Литература
1. М. Коэн, Г. Глэдстоун, М. Йенсен, Дж. Шриффер. Сверхпроводимость полупроводников и переходных металлов. Мир, М. (1972). 316 с.
2. В.Н. Александров, Е.М. Гершензон, А.П. Мельников, Н.А. Серебрякова. ЖЭТФ, 70, 4, 586 (1976).
3. В.Ф. Банная, Л.И. Веселова, Е.М. Гершензон. ФТП 23, 2, 338 (1989).
4. С.А. Немов, П.А. Осипов, В.И. Прошин, Р.В. Парфеньев, Д.В. Шамшур, Н.П. Шайнова. ФТТ 42, 7, 1180 (2000).
5. A. Blom, M.A. Odnoblyudov, I.N. Yassievich, K.A. Chao. Phys. Rev. B, V.65, 155302 (2002).
6. Ф. Блатт. Физика электронной проводимости в твердых телах. Мир, М. (1971). 472 с.
7. I.N. Yassievich, A. Blom, A.A. Prokofiev, M.A. Odnoblyudov, K.A. Chao. Physica B 308-310, 1129 (2001).
Публикации с ключевыми словами: сверхпроводники, резонансное рассеяние
Публикации со словами: сверхпроводники, резонансное рассеяние
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



