научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 03, март 2010
УДК 519.6
МГТУ им. Н.Э. Баумана,
105005, Москва, 2-я Бауманская ул., д.5.
Введение
Работа является продолжением серии работ, посвященных адаптивным методам решения непрерывной конечномерной задачи многомерной многокритериальной оптимизации (МКО-задачи), основанным на аппроксимации функции предпочтений лица, принимающего решение (ЛПР) [1]. Работа посвящена одному из методов этого класса – методу, основанному на аппроксимации функции предпочтения ЛПР с помощью многослойных персептронных сетей (MultiLayer Perceptron, MLP-сети), а также с помощью нейронных сетей с радиально-базисными функциями (Radial Basis Function Network, RBF-сети). Отметим, что методологической основой аппроксимации функций указанными сетями являются теоремы об универсальной аппроксимации [2].
В первом разделе работы представлена постановка и метод решения МКО-задачи. Во втором разделе рассматриваются особенности нейросетевой аппроксимации функции предпочтения ЛПР. Программная реализация адаптивного метода решения МКО-задачи приводится в третьем разделе. Четвертый раздел посвящен исследованию эффективности нейросетевой аппроксимации функции предпочтения ЛПР. В заключение сформулированы основные выводы и перспективы ее развития.
- Постановка и метод решения задачи
Формально непрерывную МКО – задачу можно условно записать в виде
![]() , (1)
, (1)
где ![]() - ограниченное и замкнутое в
- ограниченное и замкнутое в ![]() -мерном арифметическом пространстве
-мерном арифметическом пространстве ![]() множество допустимых значений вектора варьируемых параметров,
множество допустимых значений вектора варьируемых параметров, ![]() - векторный критерий оптимальности,
- векторный критерий оптимальности, ![]() - искомое решение МКО-задачи. Положим, что частные критерии
- искомое решение МКО-задачи. Положим, что частные критерии ![]() тем или иным образом нормализованы [1].
тем или иным образом нормализованы [1].
Множество достижимости задачи, т.е. множество, в которое векторный критерий оптимальности ![]() отображает множество
отображает множество ![]() , обозначим
, обозначим ![]() . Фронт Парето задачи (1) обозначим
. Фронт Парето задачи (1) обозначим ![]() , а множество Парето, т.е. множество векторов
, а множество Парето, т.е. множество векторов ![]() , которые порождают фронт Парето, обозначим
, которые порождают фронт Парето, обозначим ![]() .
.
Рассматривается метод решения поставленной МКО-задачи, который относится к классу прямых адаптивных методов. В этих методах ЛПР выполняет только оценку, например, в терминах «отлично», «очень хорошо», «хорошо» и т.д. предлагаемых программной системой многокритериальной оптимизации (МКО-системой) решений [3].
Метод основан на предположении существования функции предпочтений ЛПР ![]() , которая определена на множестве
, которая определена на множестве ![]() и выполняет его отображение во множество действительных числе R, т.е.
и выполняет его отображение во множество действительных числе R, т.е.
![]() .
.
При этом задача многокритериальной оптимизации сводится к задаче выбора вектора ![]() такого, что
такого, что
![]() ,
, ![]() .
.
Отметим, что функция предпочтений ЛПР заранее не известна и может быть приближенно сформирована только в процессе диалога ЛПР с МКО-системой. Предполагается, что при предъявлении ЛПР вектора параметров X, а также соответствующих значений всех критериев оптимальности ![]() , ЛПР может оценить соответствующее значение функции предпочтений
, ЛПР может оценить соответствующее значение функции предпочтений ![]() .
.
Задачу (1) решаем методом скалярной свертки. Способ свертки не фиксируется – это может быть аддитивная свертка, мультипликативная свертка, свертка Джоффриона и другие свертки [3].
Обозначим операцию свертки ![]() , где
, где ![]() - вектор весовых множителей,
- вектор весовых множителей, ![]()
![]() - множество допустимых значений этого вектора.
- множество допустимых значений этого вектора.
При каждом фиксированном векторе ![]() метод скалярной свертки сводит решение задачи (1) к решению однокритериальной задачи (ОКО-задачи) глобальной условной оптимизации
метод скалярной свертки сводит решение задачи (1) к решению однокритериальной задачи (ОКО-задачи) глобальной условной оптимизации
![]() ,
, ![]() . (2)
. (2)
В силу ограниченности и замкнутости множества ![]() решение этой задачи существует [3].
решение этой задачи существует [3].
Если при каждом ![]() решение задачи (2) единственно, то это условие ставит в соответствие каждому из допустимых векторов
решение задачи (2) единственно, то это условие ставит в соответствие каждому из допустимых векторов ![]() единственный вектор
единственный вектор ![]() и соответствующие значения частных критериев оптимальности
и соответствующие значения частных критериев оптимальности ![]() . Это обстоятельство позволяет полагать, что функция предпочтений ЛПР определена не на множестве
. Это обстоятельство позволяет полагать, что функция предпочтений ЛПР определена не на множестве ![]() , а на множестве
, а на множестве ![]() :
:
![]() .
.
В результате МКО-задача сводится к задаче выбора вектора ![]() такого, что
такого, что
![]() ,
, ![]() . (3)
. (3)
Поскольку обычно ![]() , переход от задачи (1) к задаче (3) важен с точки зрения уменьшения вычислительных затрат.
, переход от задачи (1) к задаче (3) важен с точки зрения уменьшения вычислительных затрат.
Заметим, что если используется аддитивная свертка и множество достижимости ![]() является выпуклым, то выражение (2) задает взаимно однозначное отображение множества
является выпуклым, то выражение (2) задает взаимно однозначное отображение множества ![]() во множество
во множество ![]() . В этих условиях для любого
. В этих условиях для любого ![]() вектор
вектор ![]() , являющийся решением задачи (2), принадлежит множеству Парето
, являющийся решением задачи (2), принадлежит множеству Парето ![]() . Если вместо аддитивной свертки используется свертка Джоффриона, то для получения того же результата не требуется выпуклость множества достижимости [3].
. Если вместо аддитивной свертки используется свертка Джоффриона, то для получения того же результата не требуется выпуклость множества достижимости [3].
Величина ![]() в работе полагается лингвистической переменной со значениями от «Очень-очень плохо» (
в работе полагается лингвистической переменной со значениями от «Очень-очень плохо» (![]() ) до «Отлично» (
) до «Отлично» (![]() ), где
), где ![]() - ядро нечеткой переменной
- ядро нечеткой переменной ![]() [1].
[1].
В результате МКО-задача сводится к задаче отыскания вектора ![]() , обеспечивающего максимальное значение дискретной функции
, обеспечивающего максимальное значение дискретной функции ![]() :
:
![]() ,
, ![]() . (4)
. (4)
Общая схема рассматриваемого метода является итерационной и состоит из следующих основных этапов.
Этап «разгона» метода. МКО-система некоторым образом (например, случайно) последовательно генерирует ![]() векторов
векторов ![]() и для каждого из этих векторов выполняет следующие действия:
и для каждого из этих векторов выполняет следующие действия:
1) решает задачу однокритериальной оптимизации (ОКО-задачу)
![]() ,
, ![]() ; (5)
; (5)
2) предъявляет ЛПР найденное решение ![]() , а также соответствующие значение всех частных критериев оптимальности
, а также соответствующие значение всех частных критериев оптимальности ![]() ;
;
3) ЛПР оценивает эти данные и вводит в систему соответствующее значение своей функции предпочтений ![]() .
.
Первый этап. На основе всех имеющихся в МКО-системе значений ![]() вектора
вектора ![]() и соответствующих оценок функции предпочтений
и соответствующих оценок функции предпочтений ![]() МКО-система выполняет следующие действия:
МКО-система выполняет следующие действия:
1) строит функцию ![]() , аппроксимирующую функцию
, аппроксимирующую функцию ![]() ;
;
2) отыскивает максимум функции ![]() – решает ОКО-задачу
– решает ОКО-задачу
![]() ,
, ![]() ; (6)
; (6)
3) с найденным вектором ![]() решает ОКО-задачу вида (5) – находит вектор параметров и соответствующие значения частных критериев оптимальности, а затем предъявляет их ЛПР.
решает ОКО-задачу вида (5) – находит вектор параметров и соответствующие значения частных критериев оптимальности, а затем предъявляет их ЛПР.
ЛПР оценивает указанные данные и вводит в систему соответствующее значение своей функции предпочтений ![]() .
.
Второй этап. На основе всех имеющихся в системе значений ![]() вектора
вектора ![]() и соответствующих оценок функции предпочтений
и соответствующих оценок функции предпочтений ![]() МКО-система выполняет аппроксимацию функции
МКО-система выполняет аппроксимацию функции ![]() - строит функцию
- строит функцию ![]() и т.д. по схеме первого этапа до тех пор, пока ЛПР не примет решение о прекращении вычислений. На всех этапах ЛПР имеет возможность переоценить ранее введенные им оценки.
и т.д. по схеме первого этапа до тех пор, пока ЛПР не примет решение о прекращении вычислений. На всех этапах ЛПР имеет возможность переоценить ранее введенные им оценки.
2. Особенности нейросетевой аппроксимации функции предпочтения ЛПР
Аппроксимация функции предпочтения ЛПР нейронными сетями имеет в работе ту особенность, что процесс обучения нейронных сетей происходит в условиях малой обучающей выборки. Это обстоятельство обусловлено тем, что количество «разгонных» итераций не должно быть слишком большим, иначе ЛПР просто прекратит процесс вычислений, не получив окончательного решения. Как следствие, для аппроксимации функции предпочтения ЛПР в работе используются только двухслойные MLP и RBF нейронные сети, архитектура которых представлена на рисунке 1.
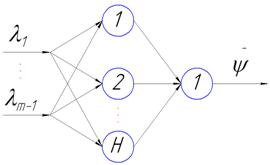
Рис. 1. Архитектура используемых нейронных сетей: (m - 1) - количество входов сети;
![]() - количество нейронов скрытого слоя
- количество нейронов скрытого слоя
Поскольку на компоненты вектора весовых множителей ![]() наложено ограничение
наложено ограничение ![]() , один из весовых множителей (пусть это будет множитель
, один из весовых множителей (пусть это будет множитель ![]() ) можно выразить через остальные множители:
) можно выразить через остальные множители: ![]() . Вследствие этого, в качестве входов нейронных сетей рассматриваются только компоненты
. Вследствие этого, в качестве входов нейронных сетей рассматриваются только компоненты ![]() ,
, ![]()
![]() вектора
вектора ![]() .
.
ЛПР в процессе решения МКО–задачи может переоценивать результаты предыдущих итераций, указанные им оценки могут быть противоречивы. Это требует постоянной корректировки обучающих данных. В работе была принята следующая стратегия корректировки.
1) Если для текущего вектора ![]() имеет место ситуация
имеет место ситуация ![]() , где
, где ![]() , и
, и ![]() , то вектор
, то вектор ![]() не включается в обучающую выборку, а генерируется новый вектор
не включается в обучающую выборку, а генерируется новый вектор ![]() . Здесь
. Здесь ![]() - некоторая положительная константа,
- некоторая положительная константа, ![]() - символ евклидовой нормы,
- символ евклидовой нормы, ![]() - некоторая целочисленная константа. Иначе говоря, если текущий вектор
- некоторая целочисленная константа. Иначе говоря, если текущий вектор ![]() оказывается слишком «близким» к некоторому вектору
оказывается слишком «близким» к некоторому вектору ![]() из обучающей выборки, и вектору
из обучающей выборки, и вектору ![]() при этом соответствует значение функции предпочтений ЛПР, далекое от решения задачи, то вместо вектора
при этом соответствует значение функции предпочтений ЛПР, далекое от решения задачи, то вместо вектора ![]() генерируется новый вектор
генерируется новый вектор ![]() . Такая стратегия призвана обеспечить выход процесса поиска из точки локального экстремума функции
. Такая стратегия призвана обеспечить выход процесса поиска из точки локального экстремума функции ![]() , аппроксимирующей функцию предпочтений (рис. 2). Величины
, аппроксимирующей функцию предпочтений (рис. 2). Величины ![]() ,
, ![]() являются свободными параметрами алгоритма.
являются свободными параметрами алгоритма.
2) Если для текущего вектора ![]() имеет место ситуация
имеет место ситуация ![]() ,
, ![]() , но
, но ![]() , то из обучающей выборки исключаются вектор
, то из обучающей выборки исключаются вектор ![]() , а также соответствующая оценка
, а также соответствующая оценка ![]() . Здесь
. Здесь ![]() - некоторая положительная константа,
- некоторая положительная константа, ![]() - вектор, содержащийся в текущий момент времени в обучающей выборке. Другими словами, если для двух совпадающих или «близко» расположенных векторов
- вектор, содержащийся в текущий момент времени в обучающей выборке. Другими словами, если для двух совпадающих или «близко» расположенных векторов ![]() заданы не совпадающие оценки функции предпочтений ЛПР, то в обучающей выборке остаются только последний по времени вектор
заданы не совпадающие оценки функции предпочтений ЛПР, то в обучающей выборке остаются только последний по времени вектор ![]() и соответствующая оценка функции предпочтений. Величина
и соответствующая оценка функции предпочтений. Величина ![]() является свободным параметром алгоритма.
является свободным параметром алгоритма.

Рис. 2. К стратегии корректировки обучающей выборки: ![]()
3. Программная реализация метода
Средствами известного программного комплекса MatLab 7.0 [4] разработана программа PREF-NNW, реализующая рассматриваемый метод решения МКО-задачи. Реализация нейронных сетей выполнена с использованием функций пакета «Neural Network Toolbox».
Для обучения MLP–сети использовался один из самых эффективных и одновременно простых методов обучения - модифицированный метод обратного распространения ошибки RPROP (Resilent back PROPagation). Отметим, что этот метод предполагает пакетный режим обучения (batch mode или offline режим), который состоит в том, что корректировка весов нейронной сети производится после обработки всех примеров обучающей выборки (эпохи) [5].
Суть метода, используемого для обучения RBF-сети, состоит в добавлении на каждой итерации в скрытый слой по одному нейрону до тех пор, пока не будет достигнут допустимый уровень ошибки обучения. Максимальное количество нейронов ограничивается размером обучающей выборки.
В качестве функции ошибки обучения для обеих сетей использовалась среднеквадратическая ошибка.
ОКО-задачи глобальной условной оптимизации (5) и (6) решались методом последовательного квадратичного программирования SQP (Sequential Quadratic Programming), из пакета «Optimization Toolbox» программного комплекса MatLab, в комбинации с методом мультистарта (из 100 случайных начальных точек) [4].
Программа PREF-NNW предоставляет в распоряжение ЛПР механизм просмотра и корректировки сделанных им ранее оценок функции предпочтений. Например, ЛПР может понизить или повысить свои оценки, «откатиться» на заданное количество итераций и пр. Для интерактивного взаимодействия программы PREF-NNW с ЛПР реализован графический интерфейс.
4. Исследование эффективности метода
С помощью программы PREF-NNW выполнено исследование погрешности нейросетевой аппроксимации функции предпочтений ЛПР для двух двумерных двухкритериальных задач и одной трехмерной трехкритериальной задачи. В качестве критерия останова было выбрано условие достижения максимума функции предпочтения с максимальной оценкой равной 9. В качестве допустимого уровня ошибки обучения во всех случаях использовалась величина 0.1.
Исследование вышеперечисленных МКО–задач проводилось на MLP-сетях с тремя, пятью, семью, девятью нейронами в скрытом слое и RBF–сети, которые далее обозначаются NN_MLP3, NN_MLP5, NN_MLP7, NN_MLP9 и NN_RBF, соответственно. Для каждой двухкритериальной и трехкритериальной задачи использовалось три (k=3) и пять (k=5) «разгонных» векторов ![]() .
.
Напомним, что для двухкритериальной задачи вектор ![]() , а для трехкритериальной -
, а для трехкритериальной - ![]() .
.
Приняты следующие обозначения:
· NN – вариант исследуемой сети (например, NN_MLP3, NN_ MLP5 и т.д.);
· I – количество итераций;
· ![]() – время обучения нейронной сети, с;
– время обучения нейронной сети, с;
· ![]() – время оптимизации аддитивной свертки частных критериев оптимальности, с;
– время оптимизации аддитивной свертки частных критериев оптимальности, с;
· ![]() – время оптимизации аппроксимированной функции предпочтения, с;
– время оптимизации аппроксимированной функции предпочтения, с;
· ![]() – оценка математического ожидания величины
– оценка математического ожидания величины ![]() ;
;
· ![]() – оценка математического ожидания величины
– оценка математического ожидания величины ![]() ;
;
· ![]() – оценка математического ожидания величины
– оценка математического ожидания величины ![]() ;
;
· ![]() – оценка математического ожидания количества эпох, которое потребовалось для обучения исследуемой MLP – сети;
– оценка математического ожидания количества эпох, которое потребовалось для обучения исследуемой MLP – сети;
· ![]() – абсолютная ошибка аппроксимации на i – ой итерации
– абсолютная ошибка аппроксимации на i – ой итерации ![]() ;
;
· ![]() – оценка математического ожидания величины
– оценка математического ожидания величины![]() ;
;
· ![]() – оценка математического ожидания абсолютной ошибки аппроксимации
– оценка математического ожидания абсолютной ошибки аппроксимации
![]() ,
,
где i – номер итерации, ![]() – размер обучающей выборки на i – ой итерации;
– размер обучающей выборки на i – ой итерации;
· ![]() – оценка математического ожидания величины
– оценка математического ожидания величины ![]() ;
;
· ![]() – максимальное значение абсолютной ошибки, достигнутой на итерациях
– максимальное значение абсолютной ошибки, достигнутой на итерациях
![]() ,
,
где i – номер итерации, j – номер примера из обучающей выборки, ![]() .
.
4.1. Двухкритериальная задача 1:
![]() ;
; ![]() ;
;
![]() .
.
Заметим, что задача имеет выпуклый фронт Парето (рис. 3).

Рис. 3. Множество достижимости ![]() задачи 1
задачи 1
В качестве оптимальных решений ЛПР рассматривал те решения, при которых значения критериев оптимальности принадлежат следующим диапазонам:
![]() ;
; ![]() .
.
Результаты исследования задачи 1 сведены в таблицы 1, 2, которые иллюстрируют рисунки 4, 5.
На рисунках 4, 5 и аналогичных последующих рисунках, если не оговорено противное, приняты следующие обозначения: число рядом с графиком – номер итерации; темный кружок соответствует значению функции предпочтения ЛПР на конечной итерации; белый кружок – значению функции предпочтения ЛПР на промежуточных итерациях, в число которых входят и «разгонные» итерации.
Таблица 1. Результаты исследования задачи 1 при k=3
|
НС |
I |
|
|
|
|
|
|
|
|
NN_MLP3 |
9 |
1.5 |
0.7 |
13.6 |
5 |
5.7 |
0.4 |
1.4 |
|
NN_MLP5 |
5 |
1.2 |
1.0 |
19.2 |
6 |
3.4 |
0.5 |
1.6 |
|
NN_MLP7 |
10 |
1.5 |
0.7 |
15.7 |
6 |
1.3 |
0.4 |
1.1 |
|
NN_MLP9 |
9 |
1.9 |
0.8 |
16.9 |
5 |
0.5 |
0.3 |
0.9 |
|
NN_RBF |
5 |
1.6 |
0.3 |
10.0 |
- |
4.8 |
0.7 |
2.8 |
Таблица 2. Результаты исследования задачи 1 при k=5
|
НС |
I |
|
|
|
|
|
|
|
|
NN_MLP3 |
7 |
1.3 |
10.0 |
14.9 |
100 |
2.3 |
0.7 |
1.3 |
|
NN_MLP5 |
7 |
1.0 |
1.0 |
14.7 |
7 |
2.5 |
0.5 |
1.8 |
|
NN_MLP7 |
6 |
1.0 |
2.0 |
15.2 |
12 |
1.9 |
0.5 |
1.9 |
|
NN_MLP9 |
7 |
0.9 |
2.1 |
18.2 |
16 |
2.3 |
0.5 |
1.9 |
|
NN_RBF |
6 |
1.0 |
1.1 |
20.0 |
- |
0.9 |
0.0 |
0.9 |

Рис. 4. Результаты исследования задачи 1: MLP-сеть c 5 нейронами; k=3

Рис. 5. Результаты исследования задачи 1: MLP-сеть с 9 нейронами; k=3
Результаты исследования показывают следующее.
1) Максимальное количество итераций, которое потребовалось для решения задачи 1 при трех «разгонных» векторах ![]() равно 10, при пяти – 7 итераций.
равно 10, при пяти – 7 итераций.
2) Для MLP-сети при k=3 «разгонных» векторах величина ![]() изменяется от ~0.9 до ~1.6. При k=5 эта величина находится в пределах от ~1.3 до ~1.9, что практически не отличается от результатов, полученных при k=3.
изменяется от ~0.9 до ~1.6. При k=5 эта величина находится в пределах от ~1.3 до ~1.9, что практически не отличается от результатов, полученных при k=3.
3) При решении задачи 1 на MLP–сетях с числом нейронов в скрытом слое больше 5 начинает сказываться эффект «переобучения» нейронной сети (рис. 5).
4.2. Двухкритериальная задача 2:
![]() ;
;  ;
;
![]() ;
; ![]() .
.
Задача представляет собой одну из задач стандартного тестового набора для многокритериальной оптимизации [6]. Множество достижимости этой задачи имеет сложную структуру, фронт Парето невыпуклый (рис. 6).
В качестве оптимальных решений в задаче 2 ЛПР рассматривал значения критериев, принадлежащие следующим диапазонам:
![]() ;
; ![]() .
.

Рис. 6. Множество достижимости ![]() задачи 2
задачи 2
Аналогично результатам, полученным в задаче 1, результаты исследования задачи 2 сведены в таблицы 3, 4, которые иллюстрируют рисунки 7, 8.
Таблица 3. Результаты исследования задачи 2 при k=3
|
NN |
i |
|
|
|
|
|
|
|
|
NN_MLP3 |
6 |
2.3 |
1.6 |
11.2 |
14 |
1.3 |
0.3 |
0.9 |
|
NN_MLP5 |
5 |
1.9 |
0.7 |
10.3 |
4 |
5.0 |
0.6 |
2.5 |
|
NN_MLP7 |
7 |
2.0 |
0.6 |
7.1 |
5 |
1.3 |
0.3 |
0.6 |
|
NN_MLP9 |
5 |
1.9 |
1.5 |
9.7 |
10 |
1.1 |
0.7 |
2.6 |
|
NN_RBF |
6 |
3.3 |
0.2 |
10.3 |
- |
186.9 |
13.0 |
64.4 |
Таблица 4. Результаты исследования задачи 2 при k=5
|
NN |
i |
|
|
|
|
|
|
|
|
NN_MLP3 |
6 |
2.0 |
3.8 |
19.1 |
26 |
0.5 |
0.2 |
0.1 |
|
NN_MLP5 |
6 |
2.2 |
2.5 |
15.8 |
18 |
0.6 |
0.3 |
0.3 |
|
NN_MLP7 |
8 |
2.32 |
2.0 |
13.1 |
15 |
7.5 |
0.9 |
5.0 |
|
NN_MLP9 |
15 |
2.0 |
1.1 |
19.6 |
9 |
7.9 |
0.4 |
1.9 |
|
NN_RBF |
7 |
2.2 |
0.3 |
15.0 |
- |
2.8 |
0.3 |
1.8 |
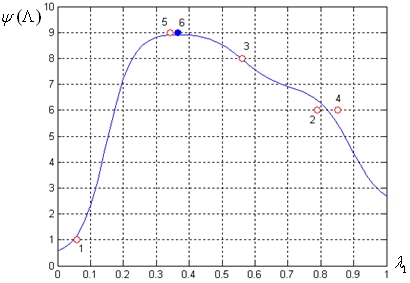
Рис. 7. Результаты исследования задачи 2: MLP-сеть c 3 нейронами; k=3
Для задачи 2 были проведены дополнительные исследования, в которых оценивалось влияние «разгонных» векторов ![]() на результаты решения задачи. Проведено три эксперимента при трех различных векторах
на результаты решения задачи. Проведено три эксперимента при трех различных векторах ![]() . В качестве нейронной сети, рассматривалась MLP–сеть с тремя нейронами в скрытом слое (NN_MLP3). Результаты исследования сведены в таблицу 5.
. В качестве нейронной сети, рассматривалась MLP–сеть с тремя нейронами в скрытом слое (NN_MLP3). Результаты исследования сведены в таблицу 5.
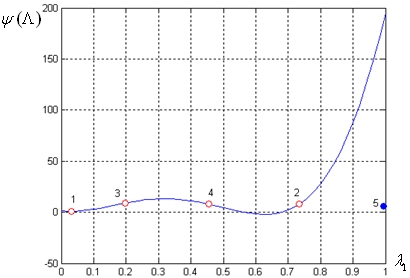
Рис. 8. Результаты исследования задачи 2: RBF-сеть; k=3; итерации ╧ 5
Исследование показало, что для рассмотренного набора векторов ![]() величина
величина ![]() изменяется незначительно от ~2.2 до ~4, а величина
изменяется незначительно от ~2.2 до ~4, а величина ![]() изменяется более существенно - от ~0.4 до ~1.4. Для каждого из рассмотренных векторов
изменяется более существенно - от ~0.4 до ~1.4. Для каждого из рассмотренных векторов ![]() потребовалось провести от 5 до 7 итераций. Таким образом, как и ожидалось, различные «разгонные» вектора
потребовалось провести от 5 до 7 итераций. Таким образом, как и ожидалось, различные «разгонные» вектора ![]() могут оказывать существенное влияние на ход решения задачи.
могут оказывать существенное влияние на ход решения задачи.
Таблица 5. Влияние «разгонных» векторов в задаче 2
|
╧ |
NN |
i |
|
|
|
|
|
|
|
|
1 |
NN_MLP3 |
5 |
2.0 |
5.9 |
10.8 |
54 |
2.2 |
0.5 |
1.4 |
|
2 |
NN_MLP3 |
6 |
2.0 |
0.8 |
12.0 |
5 |
4.0 |
1.5 |
0.4 |
|
3 |
NN_MLP3 |
7 |
1.8 |
7.0 |
16.1 |
70 |
3.1 |
0.6 |
0.4 |
В целом, по задаче 2 можно сформулировать следующие выводы.
1) Максимальное количество итераций, которое потребовалось для решения задачи при трех «разгонных» векторах равно 7, при пяти «разгонных» векторах – 15. Увеличение количества этих векторов не всегда улучшает результат решения задачи 2.
2) Большая погрешность аппроксимации RBF–сети связана с плохими экстраполяционными свойствами этих сетей (рис. 8).
4.3. Трехкритериальная задача 3:
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Отметим, что данная задача имеет выпуклый фронт Парето.
В данной задаче в качестве оптимальных решений ЛПР рассматривал значения критериев оптимальности, принадлежащие следующим диапазонам:
![]() ;
; ![]() ;
; ![]() .
.
Результаты исследования сведены в таблицы 6 и 7. Линии уровня аппроксимирующих функций представлены на соответствующих рисунках 9, 10.
Результаты исследования задачи 3 показывают следующее.
1) Максимальное количество итераций, которое потребовалось для решения задачи 3 при трех «разгонных» векторах равно 13, при пяти векторах – 17.
2) При пяти «разгонных» векторах максимальная ошибка аппроксимации достигнута на RBF–сети, что, как было отмечено выше, связано с плохими экстраполяционными свойствами этих сетей.
3) Решения задачи 3 на MLP–сетях потребовало больше итераций, чем на RBF-сети (рис. 9, 10).
Таблица 6. Результаты исследования задачи 3 при ![]()
|
NN |
I |
|
|
|
|
|
|
|
|
NN_MLP3 |
7 |
1.0 |
1.0 |
35.9 |
10 |
2.9 |
0.4 |
1.2 |
|
NN_MLP5 |
13 |
1.2 |
2.9 |
20.6 |
22 |
4.0 |
0.4 |
1.2 |
|
NN_MLP7 |
13 |
1.1 |
3.5 |
43.3 |
31 |
4.0 |
0.5 |
1.6 |
|
NN_MLP9 |
8 |
1.0 |
0.4 |
39.8 |
3 |
0.6 |
0.3 |
0.5 |
|
NN_RBF |
5 |
1.1 |
0.3 |
32.9 |
- |
2.1 |
0.3 |
1.1 |
Таблица 7. Результаты исследования задачи 3 при ![]()
|
NN |
I |
|
|
|
|
|
|
|
|
NN_MLP3 |
17 |
1.2 |
6.1 |
41.0 |
50 |
3.8 |
0.3 |
1.2 |
|
NN_MLP5 |
7 |
1.3 |
1.8 |
28.9 |
12 |
2.3 |
0.5 |
1.6 |
|
NN_MLP7 |
13 |
1.2 |
1.4 |
17.4 |
11 |
4.9 |
0.3 |
2.4 |
|
NN_MLP9 |
8 |
1.2 |
1.5 |
35.4 |
10 |
2.4 |
0.5 |
1.8 |
|
NN_RBF |
7 |
1.1 |
0.3 |
21.4 |
- |
97.7 |
8.5 |
51.1 |

Рис. 9. Результаты исследования задачи 3: RBF–сеть; k=3
Заключение
Исследование погрешности нейросетевой аппроксимации функции предпочтений ЛПР показало, что для решения двухкритериальной задачи наиболее подходящими являются MLP–сети с тремя и пятью нейронами в скрытом слое, а для трехкритериальной задачи – MLP–сеть с пятью нейронами. Для двухкритериальной задачи достаточным оказалось три «разгонных» вектора, для трехкритериальной задачи – пять векторов. Все сети, обеспечили нахождение максимума функции предпочтений. Максимальная ошибка аппроксимации была получена на RBF–сети, что связано с плохими экстраполяционными свойствами этих сетей.

Рис. 10. Результаты исследования задачи 3: MLP–сеть с 7 нейронами; k=5
В развитии работы предполагается сравнить эффективность нейросетевой аппроксимации функции предпочтений с эффективностью аппроксимации этой функции симплекс – планами, регрессионными планами второго порядка, а также нечеткими функциями. Кроме того, планируется сравнить эффективность рассматриваемого метода с эффективностью других адаптивных методов решения МКО-задачи (например, метода, реализованного в известной МКО-системе NIMBUS [7]), а также провести апробацию метода на реальной, практически значимой МКО–задаче.
Автор сердечно благодарит своего научного руководителя д.ф.-м.н., профессора МГТУ им. Н.Э. Баумана Карпенко А.П. за всестороннюю помощь и поддержку в процессе работы.
Литература
1. Карпенко, А.П., Федорук, В.Г. Адаптивные методы решения задачи многокритериальной оптимизации, использующие аппроксимацию функции предпочтений лица, принимающего решения // Наука и образование: электронное научно-техническое издание, 2008, 8, (http://technomag.edu.ru/doc/101804.html).
2. Хайкин, С. Нейронные сети. Полный курс.– М.: ООО «И.Д.Вильямс», 2008.- 415 с.
3. Лотов, А.В. Введение в экономико-математическое моделирование. – М.: Наука, 1984.- 392 с.
4. The MathWorks. Documentation. Documentation for MathWorks products, R2009b. Режим доступа: http://www.mathworks.com/access/helpdesk/help/helpdesk.html, свободный.
5. Riedmilller, M. and Braun, H. A direct adaptive method for faster backpropagation learning: The RPROP algorithm. In Proceedings of the IEEE International Conference on Neural Networks 1993 (ICNN 93), San Francisco – USA, 1993, p. 586-591.
6. Лобарева, И.Ф. и др. Многоцелевая оптимизация формы лопасти гидротурбины // Вычислительные технологии, Том 11, ╧5, 2006, С.63 – 76.
7. Карпенко, А.П., Федорук, В.Г. Обзор программных систем многокритериальной оптимизации. Отечественные системы //Информационные технологии, 2008, ╧1, С. 15-22.
Публикации с ключевыми словами: аппроксимация, многокритериальная оптимизация, нейронные сети
Публикации со словами: аппроксимация, многокритериальная оптимизация, нейронные сети
Смотри также:
- Аппроксимация функции предпочтений лица, принимающего решения, в задаче многокритериальной оптимизации. Методы на основе планов первого порядка
- 77-30569/280351 Исследование быстродействия нейросетевого распознавателя почерка.
- Исследование погрешности аппроксимации многомерной функции с помощью нейронных сетей с радиальными базисными функциями
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



