научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 03, март 2010
`
Синтез рационального маршрута обработки детали может быть одна из наиболее упоминаемых задач из области технологической подготовки машиностроительного производства. Она многократно обсуждалась в работах основоположников автоматизации технологического проектирования и в современных работах данной тематики [1,4,10].
Вербальная постановка задачи очень проста. Пусть дана некоторая машиностроительная деталь и выбрана технологическая система для ее производства. Достаточно легко определяется проектное решение, которое в технологической среде принято называть объемом или массивом обработки. Это совокупность технологических операторов, реализация которых в данной технологической системе, позволяет получить заданный геометрический образ и все конструкторские характеристики. Массив обработки представляет собой неупорядоченное множество технологически операторов, которое можно найти методом замощения геометрического образа детали элементарными обрабатываемыми поверхностями [10]. Для генерации технологического маршрута требуется получить построить линейное упорядочение множества технологических операторов, которое удовлетворяет многочисленным конструктивно-технологическим ограничениям.
Известны попытки описать и решить эту задачу средствами теории графов [10], при помощи аппарата математической логики [11] или как задачу дискретного математического программирования [4]. Эти постановки не были вполне корректными, поскольку неполнота, нечеткость и противоречивость исходных данных находится в очевидном противоречии с жесткой формализацией предлагаемых моделей. В работе предлагается иной подход – задача синтеза рационального технологического маршрута формулируется в терминах теории принятия решений.
Постановка задачи
Технологическая практика знает множество эвристических правил упорядочения, большая часть которых формулируется как бинарные отношения на совокупности технологических операций. Это могут быть универсальные рекомендации, прошедшие глубокую проверку на большой совокупности технологических экспериментов. В качестве примеров можно назвать предпочтения, которые следуют из принципа единства баз, принципа кратчайшей размерной цепи, разбиения процесса на этапы черновой и чистовой обработки. Некоторый предпорядок на множестве операций индуцирует способ простановки размеров, выбранные схемы базирования и величины снимаемого припуска. В любой проектной ситуации существует множество специализированных рекомендаций, учитывающих особенности конкретной детали и выбранной технологической системы.
Неупорядоченное множество технологических операторов X = {xi}, ![]() , необходимых для обработки детали будем называть исходным множеством альтернатив. Пусть на этом множестве задана исходная структура предпочтений, описывающая представления лица принимающего решение (ЛПР) о технологически корректной последовательности реализации пар операторов. В качестве ЛПР может выступать любой источник достоверных знаний, компетентность которого не подлежит обсуждению, в частном случае, это эксперт-технолог или экспертный коллектив.
, необходимых для обработки детали будем называть исходным множеством альтернатив. Пусть на этом множестве задана исходная структура предпочтений, описывающая представления лица принимающего решение (ЛПР) о технологически корректной последовательности реализации пар операторов. В качестве ЛПР может выступать любой источник достоверных знаний, компетентность которого не подлежит обсуждению, в частном случае, это эксперт-технолог или экспертный коллектив.
В этой работе мы не обсуждаем способы извлечения, представления и оценки достоверности экспертной информации. Будем считать, что итоги экспертизы представлены в виде матрицы парных сравнений ![]() порядка n. Это числовая матрица, в которой элемент aij ≥ 0, стоящий на пересечении строки i и столбца j, задает степень предпочтительности оператора xi над оператором xj. Для элементов матрицы выполняется соотношение aij ≥ aji тогда и только тогда, когда xi ≥ xj. Более точно, симметричные элементы матрицы парных сравнений aij и aji должны быть равны, если соответствующие объекты равноценны или несравнимы, обозначим эту ситуацию xi ~ xj. Если xi > xj , то должно быть aij > aji. Кроме этих оценочных условий, на элементы матрицы A обычно накладываются дополнительные калибровочные ограничения, связывающие попарно симметричные элементы aij и aji. Матрица парных сравнений формируется на основе экспертной информации ЛПР, поэтому значения aij зависят от типа экспертной процедуры и должны подчиняться так называемым калибровочным условиям. Рассмотрим основные типы калибровок.
порядка n. Это числовая матрица, в которой элемент aij ≥ 0, стоящий на пересечении строки i и столбца j, задает степень предпочтительности оператора xi над оператором xj. Для элементов матрицы выполняется соотношение aij ≥ aji тогда и только тогда, когда xi ≥ xj. Более точно, симметричные элементы матрицы парных сравнений aij и aji должны быть равны, если соответствующие объекты равноценны или несравнимы, обозначим эту ситуацию xi ~ xj. Если xi > xj , то должно быть aij > aji. Кроме этих оценочных условий, на элементы матрицы A обычно накладываются дополнительные калибровочные ограничения, связывающие попарно симметричные элементы aij и aji. Матрица парных сравнений формируется на основе экспертной информации ЛПР, поэтому значения aij зависят от типа экспертной процедуры и должны подчиняться так называемым калибровочным условиям. Рассмотрим основные типы калибровок.
- Простая структура (ПС) или простая калибровка (ПК):

Диагональные элементы при этом обычно не фиксируются и могут быть любыми. Если "i aii = ½, то ПС является разновидностью турнирной калибровки, которая рассматривается далее. Интерпретация простой калибровки достаточно прозрачна: aij – это значения факта предпочтительности одного объекта над другим или их равноценности (несравнимости).
- Турнирная калибровка (Т):
![]()
В этой калибровке aij – рассматривается как «число очков», набранных объектом xi в единоборствах с объектом xj. Число c = const при этом может интерпретироваться как количество таких встреч. Нередко дополнительно требуется целочисленность матрицы парных сравнений A.
- Степенная калибровка (С):
![]()
Эта калибровка имеет следующее толкование: объект xi превосходит в парном сравнении объект xj в aij раз.
4) Кососимметрическая калибровка (К):
![]()
Калибровка имеет следующее толкование: объект xi превосходит в парном сравнении объект xj на aij.
5) Вероятностная калибровка (В):
![]()
Толкование: aij – вероятность превосходства xi над хj.
Можно утверждать, что вероятностная калибровка – это самое популярное калибровочное условие в теории принятия решений. Это объясняется ее простотой и возможностью различных интерпретаций. В частности, численные значения парных предпочтений можно рассматривать не только как оценки вероятностей предпочтительности объектов, но и в качестве значений функции принадлежности некоторого нечеткого отношения доминирования. Для обработки таких структур предпочтений можно применить развитый аппарат теории вероятности, математической статистики и теории нечетких множеств.
Опыт технологической экспертизы показал, что для задачи упорядочения технологических операторов естественными видами калибровок будут следующие: ПК, Т и В. Вероятностная калибровка применяется особенно часто, поскольку эксперту проще оценить вероятность предпочтительности одной одного объекта над другим, нежели разность или отношение предпочтительности альтернатив.
Итак, элементы матрицы ![]() рассчитываются по итогам экспертиза, а предпочтительность операторов x понимается как предшествование в технологическом маршруте. Любую матрицу парных сравнений
рассчитываются по итогам экспертиза, а предпочтительность операторов x понимается как предшествование в технологическом маршруте. Любую матрицу парных сравнений ![]() с неотрицательными элементами ai,j ≥ 0 можно представить в виде ориентированного графа G = (X, D), в котором вершинами служат альтернативы, и две вершины xi и xj связаны дугой d=(xi, xj) Î D c весом ai,j тогда и только тогда, когда ai,j > 0. Будем называть его графом предпочтений. Очевидно, что этот граф не содержит петель и кратных дуг.
с неотрицательными элементами ai,j ≥ 0 можно представить в виде ориентированного графа G = (X, D), в котором вершинами служат альтернативы, и две вершины xi и xj связаны дугой d=(xi, xj) Î D c весом ai,j тогда и только тогда, когда ai,j > 0. Будем называть его графом предпочтений. Очевидно, что этот граф не содержит петель и кратных дуг.
В задаче принятия решений (ЗПР) требуется найти такой линейный порядок на исходном множестве альтернатив X, который является наилучшим приближением (аппроксимантой) исходной структуры предпочтений, представленной в виде матрицы парных сравнений A или графа предпочтений G.
Существует множество практических приложений, которые формулируется в терминах синтеза наилучшего линейного приближения некоторой графовой структуры, поэтому число работ данного направления очень велико. Авторами работ по теории принятия решений было предложено множество методов упорядочения [2,3,5,7,8,9], поэтому рекомендации по обоснованному выбору модели много важнее предложений по разработке новой или существенной модификации одной из существующих моделей.
Рассмотрим подход, основанный на оценке качества моделей линейного упорядочения по степени удовлетворения ими некоторых постулированных свойств [2]. Эти свойства не должны считаться аксиомами: их выполнение лишь желательно, но не обязательно, но многие из них имеют столь ясную и хорошо согласующуюся с интуицией формулировку, что их нарушение с трудом сочетается с представлениями о разумности модели упорядочения.
Произвольное линейное упорядочение объектов из Х далее будем записывать в виде вектора номеров I= (i1, ..., in), обозначая через Nm(I) номер места объекта xm в упорядочении I. Множество всевозможных упорядочений (перестановок) над Х обозначим I*. Если задана матрица парных сравнений и некоторая модель упорядочения, множество оптимальных с ее точки зрения упорядочений будет обозначаться I*opt(A); |I*opt (A)| ³ 1.
Свойства моделей упорядочения
Рассмотрим в первую очередь возможные изменений множества I*opt(A) в зависимости от допустимых изменений исходной матрицы парных сравнений А.
Свойство 1. Инвариантность к растяжению (ИР). Умножение всех элементов A на положительную константу не изменяет оптимальных упорядочений:
![]()
Свойство 2. Инвариантность к сдвигу (ИС). Замена всех элементов aij на аij+b, где b — произвольная положительная константа, не влияет на множество оптимальных упорядочений:
![]()
Свойство 3. Транспонируемость (Т). Замена всех предпочтений на «прямо противоположные», т. е. инверсия всех дуг в структуре предпочтений, должна приводить к тотальной инверсии оптимальных упорядочений:
![]()
где AT – транспонированная матрица парных сравнений, описывающая инвертированную структуру предпочтений, а IT — зеркально инвертированное упорядочение I (если I= (i1, ..., in), то IT=(in,...,i1)).
Свойство 4. Устойчивость «в малом» (УМ). Достаточно малые допустимые изменения матрицы A должны сохранять оптимальность хотя бы одного элемента из I*opt (А).
Свойство 5. Положительная реакция (ПР). Изменение результата отдельного парного сравнения между хi, и xj в пользу хi не должно приводить к ухудшению места, занимаемого объектом xi в оптимальном упорядочении. Если I Î I*opt(A) и матрица B отличается от A только элементами bij и bji, причем bij³ аij и bji£ аij, то найдется такое I'ÎI*opt(В), что Ni(I') £ Ni(I).
Ряд следующих свойств связан с доминированием объектов в исходной структуре предпочтений.
Свойство 6. Сохранение доминирования (СД). Будем говорить, что объект xi строго доминирует над объектом хj в данной структуре предпочтений (обозначая это хi>>xj), если во всех парных сравнениях объект хi проявляет себя хотя бы не хуже, чем xj, и хотя бы в одном – строго лучше:
![]()
причем хотя бы одно из этих неравенств – строгое.
Очевидно, что «разумная» модель линейного упорядочения должна в подобном случае помещать доминирующий объект выше подчиненного, т.е. сохранять доминирование.
Свойство СД также выглядит весьма естественным и желательным, так что отсутствие его у той или иной модели следует считать серьезным недостатком.
Свойство 7. Сегментируемость по бикомпонентам (СБ). Если структура предпочтений G = (V, U) не является сильно связным орграфом, то в ней можно выделить отдельные бикомпоненты (компоненты сильной связности), которые оказываются односторонне связанными между собой. Пусть V1, ..., Vm — множества вершин, относящихся к различным бикомпонентам, то они могут быть пронумерованы так, чтобы дуги из бикомпонент с большими номерами в бикомпоненты с меньшими номерами отсутствовали. При этом естественно заключить, что объекты бикомпоненты с меньшим номером в целом предпочтительнее объектов из бикомпоненты с большим номером и в оптимальном упорядочении должны им предшествовать.
Назовем оптимальное упорядочение кусочно-оптимальным, если отбрасывание произвольного количества объектов с самого начала или с самого конца его сохраняет оптимальность оставшегося фрагмента, т. е. произвольный связный фрагмент Irt=(ir,...,it) оптимального упорядочения I=(i1,...,ir,...,it,...,in) сам является оптимальным для соответствующей подматрицы.
Свойство 8. Кусочная оптимальность (КО). Для любой матрицы парных сравнений А любое упорядочение IÎI*opt(A) кусочно-оптимально.
Рассмотрим еще одно свойство, тесно связанное с кусочной оптимальностью. Следуя, введем на множестве Х отношение группового доминирования ![]() , определив
, определив
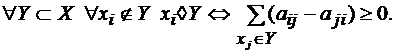
Таким образом, объект xi доминирует над группой Y, если баланс его парных сравнений с объектами из этой группы неотрицателен. Заметим, что введение такого отношения осмысленно не при любой калибровке матрицы А (например, при степенной калибровке типа понятие баланса парных сравнений, видимо, теряет смысл).
Упорядочение I=(i1,...,in) (не обязательно оптимальное) назовем локально-сбалансированным, если любой объект в нем доминирует в над любой непосредственно следующей за ним группой:
![]() (*)
(*)
Свойство 9. Локальная сбалансированность (ЛС). Любое оптимальное линейное упорядочение должно быть локально-сбалансированным.
Свойство 10. Количественная оценка важности объектов (ОВО). Построение линейного упорядочения объектов представляет собой не что иное, как получение глобальных оценок их «важности» (ценности, предпочтительности, силы и т. п.) не друг относительно друга, а в единой порядковой шкале.
В тех случаях, когда множество I*opt(A) не одноэлементно, возникает и вопрос о том, насколько сходны между собой различные оптимальные упорядочения. Для исследования его, в принципе, возможно ввести некоторую метрику на множестве I* и проанализировать, насколько далеки друг от друга различные элементы I*opt(A). Здесь же мы рассмотрим иной подход к определению понятия сходства.
Свойство 11. Сходство различных оптимальных упорядочений (СУ).
Это свойство толкуется следующим образом. Рассматривая построение линейного упорядочения как аппроксимацию исходной структуры, можно заключить, что наличие сразу нескольких оптимальных линейных упорядочений служит косвенным указанием на то, что в исходную структуру вносятся слишком большие искажения, т.е. имевшегося в структуре «внутреннего порядка» недостаточно для построения линейного упорядочения.
Свойство 12. Оценка качества аппроксимации (ОКА). В некоторых случаях, кроме поиска оптимального упорядочения, оказывается важной возможность сравнить два различных упорядочения, аппроксимирующих исходную структуру по-разному. Если в рамках некоторой модели оказывается возможным естественным образом количественно оценить качество аппроксимации исходной структуры произвольным упорядочением (тем самым оптимальным оказывается упорядочение, получающее самую высокую оценку), то это позволяет дать ответ на вопрос, насколько одно упорядочение лучше другого, а в тех случаях, когда поиск оптимума слишком сложен и трудоемок, – рассмотреть вопрос о субоптимальных или приближенных решениях.
Технологическая обоснованность свойств упорядочения
Статус свойств моделей упорядочения можно уподобить аксиоматике данной проблемной области. Их нельзя доказать или свести к совокупности более простых качеств, справедливость которых очевидна. Подобно постулатам формальных систем они принимаются как, отвечающие базовым представлениям или закономерностям. Попробуем привести аргументы в пользу технологической обоснованности перечисленных свойств, ориентируясь на упомянутую в начале статьи постановку задачи рационального упорядочения множества технологических операторов.
Представляется почти очевидным, что метод упорядочения, который не соответствует свойствам 1 – 6, имеет мало оснований считаться доброкачественным. Инвариантность к растяжению и сдвигу, а также транспонируемость – это базовые свойства любой корректной процедуры измерения. Действительно, свойство ИР можно сравнить с растяжением или сжатием (в зависимости от коэффициента) некоей многомерной шкалы, что может изменить числовые значения измерения, но сохраняет взаимное положение измеряемых точек. Свойство ИС аналогично смещению точки отсчета многомерной шкалы, что не должно повлиять на результаты качественных измерений.
Выполнимость свойств устойчивости в малом, положительной реакции и сохранения доминирования весьма желательна. Во-первых, они хорошо согласуются с интуитивными представлениями лица принимающего решение о «хороших» методах упорядочения, во-вторых, особенность решаемой задачи не противоречит перечисленным аксиомам.
Рассмотрим свойство сегментируемости по бикомпонентам. Практика показывает, что для принятия рационального решения об упорядочении технологических операторов необходимо принять учесть большой массив данных о конструкции детали и свойствах производственной системы. Это значит, что граф, описывающий структуру ЛПР, получит плотную структуру с большим числом взвешенных дуг. С очень высокой вероятностью этот граф будет сильно-связным, не допускающим разбиение на бикомпоненты. Таким образом, выполнимость свойства сегментируемости является желательным, но не обязательным.
В авторитетных публикациях по теории принятия решений [8] говорится о том, что выполнимость свойств кусочной оптимальности и локальной сбалансированности являются весьма желательным, но трудно выполнимым делом. Распространим эту оценку и на задачу синтеза рационального маршрута. Наконец, последние три свойства (ОВО, СУ и ОКА) необходимы для количественной оценки полученных решений, что можно считать необязательным для поставленной задачи.
Итак, для решения задачи синтеза технологического маршрута требуется получить метод линейного упорядочения, который гарантирует выполнение свойств 1-6, и опционально выполнимость свойств 8-9. Свойства 7, 10, 11 и 12 не будем использовать для оценки доброкачественности метода упорядочения.
Модели линейного упорядочения «спортивного типа»
В работах по автоматизации технологического проектирования в основном обсуждаются модели упорядочения, в которых используются различные варианты статистической обработки матриц парных сравнений. Каждому объекту xi сопоставляется некоторый интегральный показатель pi, оценивающий итоги его сравнений с остальными объектами, а далее объекты ранжируются по убыванию или возрастания значений этого показателя. Если же несколько объектов имеют одинаковые показатели, то для их упорядочивания могут использоваться дополнительные факторы, либо в рациональное упорядочение допускается включение этих объектов по выбору ЛПР. По причине очевидных аналогий со спортивными состязаниями, за методами этого типа в теории принятия решений закрепилось название моделей «спортивного типа». Рассмотрим несколько примеров.
В простейшем случае в качестве ранжирующего фактора используется набранная объектом «сумма очков», строчная суммы матрицы парных сравнений:

В наиболее распространенной турнирной модели объекты непосредственно упорядочиваются по убыванию таких строчных сумм. Сама обрабатываемая матрица парных сравнений А при этом может иметь калибровку типа Т или ПС, а поскольку свойства инвариантности очевидным образом выполняются, модель пригодна и для кососимметрической калибровки. Использование же ее для произвольных взвешенных структур представляется недостаточно обоснованным. Если игроки провели разное количество встреч, то набранные ими очки не отражают их реальной силы.
Широкая распространенность и популярность турнирной модели объясняется ее исключительной простотой и алгоритмической легкостью генерации оптимального упорядочения. В тех случаях, когда несколько объектов имеют одинаковые суммы очков, используются дополнительные ранжирующие показатели и коэффициенты типа количества «чистых побед» (число единиц в строке матрицы парных сравнений с вероятностной калибровкой) и др.
Легко видеть, что турнирная модель обладает положительной реакцией, сегментируемостью по бикомпонентам и полностью сохраняет доминирование, а свойствами КО, ЛС, ОКА не обладает. В тех случаях, когда |I*opt(A)|>1, все оптимальные упорядочения оказываются сходно порожденными, выполнение же свойств ИР, ИС, УМ и Т гарантируется лишь в нескольких специальных случаях. Действительно, если в оптимальном выделенном упорядочении объект xi, предшествует хj, только по дополнительным показателям, то и для матрицы AT xi также может по тем же показателям предшествовать xj (нарушение свойства Т); равенство же si=sj при сколь угодно малых изменениях в исходной матрице A может перейти в si<sj (нарушение свойства УМ). Поэтому применение турнирной модели (и ее многочисленных модификаций) для решения задачи синтеза технологического маршрута можно считать недостаточно обоснованным.
В публикациях по теории принятия решения обсуждаются многочисленные альтернативы турнирной модели, в которых вместо одношаговой процедуры оптимизации предлагаются многоступенчатые алгоритмы генерации. Рассмотрим несколько популярных многошаговых процедур.
Метод последовательного вычленения лидеров (ПВЛ) – это метод упорядочения, в котором ранжировка строится в результате многократного выбора лидера. На первом шаге в качестве лучшего выбирается объект с максимальной строчной суммой. Он помещается на первое место в итоговом упорядочении, а из матрицы парных сравнений вычеркиваются соответствующие строка и столбец, а строчные суммы пересчитываются. Далее выбирается объект, занявший вторе место, и т.д.
По основным свойствам модель ПВЛ от турнирной не отличается, однако если оптимальное упорядочение – выделенное, то гарантировать сохранение доминирования нельзя. В то же время если I=(i1, ..., in) Î I*opt(A). то и фрагменты (i2,...,in), (i3,...,in) и т. д. также оптимальны для соответствующих подматриц, так что свойство cndjерпеКО частично выполняется. Частично выполняется и свойство ЛС, ибо
![]()
т. е. любой объект доминирует над следующим за ним продолжением.
В задачах упорядочения используются и другие многоступенчатые процедуры ранжировки. Рассмотрим популярную на практике схему последовательного, когда множество Х вначале разбивается на линейно упорядоченные между собой слои, далее каждый слой сам подвергается подобному расслоению и т.д. Самый простой реализацией этого подхода является метод последовательной дихотомии (ПД), в котором исследуемый слой всякий раз делится надвое, полученные «лучшая» и «худшая» части вновь дробятся пополам и т.д.
В модели ПД к «лучшим» обычно относятся объекты с большими строчными суммами в соответствующей подматрице; при этом либо мощность подмножества лучших фиксируется, либо в него заносятся объекты, суммы очков которых превышают некий пороговый уровень. И тот и другой варианты по своим свойствам мало отличаются от остальных моделей спортивного типа, однако не обладают свойствами УМ. и ПР, что следует считать крупным недостатком.
Действительно, в первом варианте модели обычна ситуация, когда отбор объектов в «лучшую» часть производится по дополнительным показателям, но малейшие допустимые изменения в исходной матрице при этом могут такую ситуацию нарушить и привести к отбору совсем иных объектов, так что устойчивость в малом очевидным образом отсутствует. Во втором варианте к аналогичному выводу приводит анализ ситуации, в которой сумма очков объекта равна пороговому уровню. В то же время и для первого, и для второго варианта модели вполне реальна ситуация, когда изменение в пользу xi результата его сравнения с хj приводит к тому, что хj ранее попадавший в «лучшую» часть, перестает туда попадать (или заменяется на xk), что плохо сказывается на итоговом месте xi, – так что свойство ПР также отсутствует.
В рассмотренных выше моделях спортивного типа в качестве ранжирующего фактора выступала сумма набранных очков (во всей матрице или в отдельных подматрицах), и объекты упорядочивались по убыванию значений этого фактора. Можно предложить минимаксный аналог спортивных моделей, в котором сила объекта оценивается по наиболее крупному его проигрышу. Рассмотрим модель, использующую функцию доминируемости (ФД) и предназначенную для обработки нечетких предпочтений.
Если aijÎ[0,1] – степень принадлежности пары (xi, xj) к нечёткому отношению предпочтения, заданному на X, то функция доминируемости
![]()
характеризует максимальную силу, с которой объект xi доминируется остальными объектами множества X. При lX (xi) = 0 xi абсолютно не доминируется, при lX (xi) = 1 – абсолютно доминируется, при 0<lX(xi)<1 – слабо доминируется. Ранжирование объектов выполнятся по следующему простому правилу x < y, если lX(x) > lX(y).
упорядочивая объекты по убыванию соответствующих ее значений
Модель ФД предназначена для обработки матриц в калибровке В, однако ее можно адаптировать и для матриц с калибровками Т, С, К. Наличие свойств ИР и ИС совершенно очевидно, а вот свойство Т не выполняется даже при выполнении условия обратимости aij+aji=1. Справедливость свойства УМ (при обычных оговорках) сомнений не вызывает, не требуют доказательства и свойства ПР и СД, В то же время приведенный пример показывает, что модель ФД слабо допускает, Говорить о наличии свойств КО и ЛС поэтому также не приходится. Очевидно, что алгоритмическая реализация метода ФД очень проста, он сохраняет большую часть важных для задачи синтеза маршрута свойств, что делает его перспективным для применения. Это предварительное заключение, которое требует глубокой практической проверки.
Модель максимального согласования
Простейшая модель максимального согласования (МС) первоначально была предложена Слейтером для анализа матриц парных сравнений с простой калибровкой и без равноценных элементов. Подробное описание этого важного метода можно найти в [2], здесь приведем основные идеи и приемы.
Говорят, что линейный порядок I имеет элементарное рассогласование с матрицей A, если существует пара объектов (хi, xj), такая, что хi>хj, т.е. аij=1, аji=0, однако хj предшествует xi в I. Оптимальным считается максимально согласованное с A линейное упорядочение объектов, т.е. упорядочение с минимальным числом рассогласований.
Если обозначить через nA(I) – слейтерово число рассогласований I с А, а через B(I) – матрицу линейного порядка, задаваемую I, то очевидно, что
![]()
где ![]() расстояние между матрицами по Хеммингу.
расстояние между матрицами по Хеммингу.
Слейтерово число несогласий nA(I) может быть представлено и в виде  , поэтому задача отыскания оптимального упорядочения может быть записана в канонической форме:
, поэтому задача отыскания оптимального упорядочения может быть записана в канонической форме:
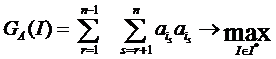 (**)
(**)
Это задачу можно интерпретировать как поиск такой перестановки строк и столбцов матрицы A, которая максимизирует сумму наддиагональных элементов. Эта задача известна под названием задачи о наилучшей приближенной триангуляции (нп-триангуляции) матрицы А. Сам же показатель GA(I) (наддиагональная сумма) может использоваться как показатель качества аппроксимации исходной структуры линейным упорядочением.
Опираясь на формальную постановку (**), модель можно обобщить и для турнирной и вероятностной калибровок, считая оптимальным (наиболее согласованным) линейное упорядочение, осуществляющее нп-триангуляцию матрицы A, т.е. максимизирующее функционал ga(i) (равный разности между суммарным весом оставляемых и отбрасываемых дуг или отличающийся от этой разности лишь на константу), смысл которого, как оценки качества аппроксимации, вполне сохраняется. Поскольку такое упорядочение является максимально согласованным, то оно остается ближайшим к исходной структуре предпочтений.
Справедливость свойств ИР и ИС для модели очевидна, а такие свойства, как ПР и Т, легко доказываются от противного. Свойство УМ сразу вытекает из того факта, что оптимальное упорядочение – ближайшее к исходной структуре предпочтений: в случае когда оно единственно, малые изменения в A оставят его ближайшим; если же таких упорядочений несколько, малые изменения в A оставят ближайшим хотя бы одно из них. Наличие у модели МС свойств СБ, КО и ЛС также легко доказывается.
В рамках модели МС возможно существование оптимальных упорядочений, не сохраняющих доминирования. Действительно, пусть I=(i1, ..., in) ÎI*opt(A), причем ![]() , однако
, однако ![]() . Тогда перестановка
. Тогда перестановка ![]() и
и ![]() приведет к иному упорядочению, не сохраняющему доминирования, однако имеющему тот же показатель качества GA, что и I, а значит, тоже оптимальному. В то же время, оптимальное упорядочение, сохраняющее доминирование, всегда найдется: если $r, s: xr>>xs, а IÎI*opt(А) не сохраняет этого доминирования, то, поменяв местами хr и хs, получим упорядочение с заведомо не худшим показателем, сохраняющее доминирование. Итак, доминирование в модели МС сохраняется частично.
приведет к иному упорядочению, не сохраняющему доминирования, однако имеющему тот же показатель качества GA, что и I, а значит, тоже оптимальному. В то же время, оптимальное упорядочение, сохраняющее доминирование, всегда найдется: если $r, s: xr>>xs, а IÎI*opt(А) не сохраняет этого доминирования, то, поменяв местами хr и хs, получим упорядочение с заведомо не худшим показателем, сохраняющее доминирование. Итак, доминирование в модели МС сохраняется частично.
Показатель GA(I), как уже отмечалось, в модели МС выступает в роли оценки качества аппроксимации, поддиагональная же сумма преобразованной (нп-триангулированной) матрицы, тесно связанная с расстоянием до ближайшего линейного порядка, может использоваться, как оценка искажений, вносимых в исходную структуру при равномерной аппроксимации, или оценка уже имеющегося в этой структуре «внутреннего» порядка.
Основное затруднение при практическом использовании модели МС состоит в том, что задача нп-триангуляции, эквивалентна известной NP-трудной проблеме о множестве дуг, разрезающих контуры, поэтому также является NP-трудной, так что получение ее оптимального решения для больших п может потребовать слишком значительного времени. Разумным при этом выглядит ограничиться локально-оптимальным решением, понимая под ним, такое упорядочение I, показатель качества GA(I) которого не может быть улучшен за счет одиночного перемещения любого объекта. Так получаемая локальная модель максимального согласования (ЛМС) обладает всеми свойствами модели МС.
Несложно убедиться в том, что локально-оптимальное упорядочение должно удовлетворять приведенному ранее соотношению (*), указывающему на невыгодность перемещения объектов сверху вниз, и двойственному соотношению
![]() (***)
(***)
указывающему на невыгодность перемещения снизу вверх. Поиск такого упорядочения весьма прост и может осуществляться в два этапа. Вначале строится некоторое начальное упорядочение, далее в нем ищутся фрагменты, на которых нарушаются соотношения (*) или (***). В первом случае объект xs помещается после xt, во втором случае xt ставится перед xs. Далее поиск продолжается и заканчивается, когда таких фрагментов не остается. Даже для больших п такая процедура быстро приводит к получению локально-оптимального упорядочения, причем разница в показателях качества искомого оптимального и так построенного локально-оптимального упорядочений обычно очень невелика (и даже более того, так построенное упорядочение нередко само оказывается оптимальным).
Для построения оптимальных упорядочений в модели МС было предложено большое число алгоритмов, использовавших идеи целочисленного линейного программирования, динамического программирования и метода ветвей и границ [2].
Выводы:
1. Задача синтеза рационального технологического маршрута обработки детали ставится как задача принятия решений. Исходная структура предпочтений формируется на основе экспертной информации об упорядоченности пар технологических операторов. Эти данные сохраняются в форме матрицы парных сравнений с простой, турнирной или вероятностной калибровками. Требуется найти линейное упорядочение операторов, которое вносит минимальные искажения в исходную структуру предпочтений.
2. Задача линейного упорядочения активно обсуждается специалистами в области теории принятия решений, теории управления, математической экономике и многих других областях знания. Предложено большое число различных моделей упорядочения: от самых простых, в которых ранжирование выполняется по строчной сумме матрицы парных сравнений, до требующих громоздких вычислений моделей, использующих статистические показатели качества и различные метрики. Выбор подходящей для решения поставленной задачи модели трудно решить простой проверкой, по причине изобилия подходов к проблеме синтеза рационального линейного упорядочения. Вслед за [2] предлагается использовать подход, основанный на постулировании свойств.
3. Проведен анализ технологической обоснованности свойств моделей линейного упорядочения, выбрано подмножество аксиом, выполнение обязательно для задачи синтеза технологического маршрута.
4. Показано, что модели «спортивного типа» и их многочисленные модификации, которые часто применяются в технологической подготовке производства, не обеспечивают выполнения некоторых важных свойств упорядочения.
5. максимального согласования сохраняет все важные для задачи синтеза технологического маршрута свойства. Алгоритмическое обеспечение этой модели поддержано многочисленными разработками. Эта классическая труднорешаемая задача имеет облегченную постановку, допускающую эффективное решение задач высокой размерности.
Литература
1. Аверченков В.И., Каштальян И.А., Пархутик А.П. САПР технологических процессов, приспособлений, и режущих инструментов. – Минск.: Вышейшая школа, 1993.
2. Белкин А.Р., Левин М.Ш. Принятие решений: комбинаторные модели аппроксимации информации. – М.: Наука, 1990.
3. Глотов В.А., Павельев В.В. Векторная стратификация. – М.: Наука, 1984.
4. Кондаков А.И. САПР технологических процессов – М.: Издательский центр Академия, 2007.
5. Ларичев О.И. Теория и методы принятия решений – М.: Логос, 2006.
6. Левченков В.С. Алгебраический подход к теории выбора. – М.: Наука, 1990.
7. Миркин Б.Г. Анализ качественных признаков и структур. М.: Статистика, 1980.
8. Орлов А.И. Теория принятия решений. – М.: Экзамен, 2006.
9. Садовский Л.Е. Садовский А.Л. Математика и спорт – М.: Наука, 1985.
10. Цветков В.Д. Системно-структурное моделирование и автоматизация проектирования технологических процессов – Минск.: Наука и техника, 1979.
11. Челищев Б.Е., Боброва И.В., Гонсалес-Сабатер А. Автоматизация проектирования технологии в машиностроении – М.: Машиностроение, 1987.
Публикации с ключевыми словами: упорядоченный поиск проектных решений
Публикации со словами: упорядоченный поиск проектных решений
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



