научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 02, февраль 2010
УДК 621.391.535.8
Задача синтеза динамически устойчивого движения двуногого шагающего робота чрезвычайно сложна. Насколько можно судить, к настоящему времени в общем виде она не решена. Однако управление динамической ходьбой можно осуществить, используя различные частные подходы. В данной статье представлены принцип и результаты синтеза программных траекторий движения двуногого шагающего робота по ровной горизонтальной поверхности в режиме динамической ходьбы при помощи упрощённой математической модели.
Воспользуемся моделью, представляющей робот состоящим из двух стержневых ног, обладающих массой и моментом инерции, и корпуса в виде точечной массы. Возмущениями, возникающими от движения ног в коленных шарнирах, а также при подъёме стоп при ходьбе, пренебрежём. Кроме того, представление корпуса точечной массой заставляет синтезировать лишь такие движения, при которых моменты инерции корпуса не проявляются, т.е. движения с постоянной ориентацией корпуса. Однако, именно такие движения представляют большой практический интерес. Также будем считать углы отклонения ног от вертикали малыми. Это позволит использовать линейные дифференциальные уравнения.
Рассматриваемая кинематическая схема представлена на рис. 1.
Примем следующие обозначения:
m1, m2 - массы опорной и переносимой ног,
J1, J2 - моменты инерции опорной и переносимой ног относительно их центров масс (примем их равными, как в сагиттальной, так и фронтальной плоскостях),
M - масса корпуса,
xk , yk – горизонтальные координаты корпуса,
xc , yc - горизонтальные координаты переносимой стопы.

Рис. 1. Принятая в данной модели кинематическая схема робота
Движения в сагиттальной и фронтальной плоскостях будем рассматривать независимо (благодаря отсутствию проскальзывания между опорной стопой и опорной поверхностью). В качестве обобщённых координат выберем горизонтальные координаты корпуса и переносимой стопы. Уравнения движения запишем, используя уравнение Лагранжа второго рода. Примем, что опорная точка находится в начале координат. Уравнения плоского движения двухзвенного механизма с одной опорной точкой при принятых допущениях и ограничениях примут вид:
система уравнений движения вдоль x

вдоль оси y
 .
.
В этих уравнениях


В форме Коши уравнения имеют вид:
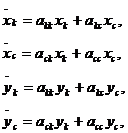
где

Биквадратное характеристическое уравнение данной системы дифференциальных уравнений имеет два действительных и два комплексных корня. Действительные корни
 .
.
Вещественная часть комплексных корней
![]() ,
,
где

![]() .
.
В этих выражениях
 .
.
Решение системы запишем в следующем виде:
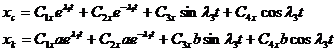 ,
,
 .
.
где
 .
.
Скорости стопы и корпуса

Для начальных условий t=0, ![]()
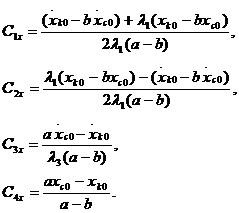

Если координаты опорной точки (xот, yот)Т, а начальные условия заданы для момента времени t0, то

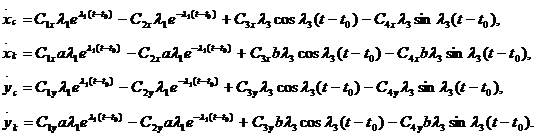
Рассмотрим симметричный относительно критической точки (корпус над опорной стопой, обе ноги вертикальны) шаг, при помощи которого реализуется ходьба с постоянной средней скоростью. В этом случае стопа и корпус проходят критическую точку одновременно. Положим, также, в начальный момент времени t=0. Зададимся средней скоростью движения vср, и коэффициентом двухопорности K.
Найдём такие начальные скорости vk0 , vc0 и время движения T, чтобы к концу одноопорной фазы при заданной средней скорости выполнялось соотношение
![]() ,
,
а скорость движения переносимой стопы равнялась нулю vc1=0.
Для этого необходимо решить следующую систему уравнений:
 .
.
Для того, чтобы решать её численно методом Ньютона необходимы следующие частные производные:


Спустя время T1 от критического начинается двухопорная фаза движения. В двухопорной фазе переносимая стопа неподвижна. Пусть опорная точка находится в начале координат. Соответствующие уравнения движения корпуса имеют вид:
![]()
![]() .
.
Коэффициенты этого уравнения вычисляются по прежним формулам.
Однородное уравнение движения корпуса вдоль оси x имеет вид:
![]() .
.
Его характеристическое уравнение имеет два корня l2 и -l2,
где
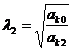 .
.
Если в начальный момент времени t=t0, а координаты опорной точки (xот,yот), уравнения движения корпуса вдоль оси x в двухопорной фазе запишем в виде:

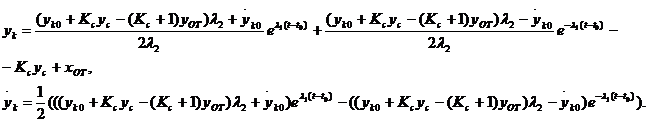
где
![]() .
.
Продолжительность двухопорной фазы T2 (время, за которое корпус переходит из положения xk1 в положение xk2 = xc1/2)

Пусть сагиттальная плоскость ориентирована вдоль оси x, фронтальная, соответственно вдоль оси y. Тогда приведенные уравнения движения вдоль оси х позволяют синтезировать движение в сагиттальной плоскости, рассчитать длительность (от критического положения) T1 одноопорной фазы и T2 двухопорной фазы (до момента смены опорной ноги). Общая длительность полушага Tп равна их сумме
![]() .
.
Если ширина следовой дорожки постоянна, можно принять, что движение переносимой стопы вдоль оси x совершается в вертикальной плоскости, параллельной оси x. Таким образом, на протяжении всего шага координата y переносимой стопы остаётся неизменной, и для синтеза движения робота вдоль y на протяжении всего Tп можно использовать уравнения, полученные для двухопорной фазы.
Для обеспечения периодического движения с постоянной скоростью вдоль x необходимо, чтобы в начале шага скорость корпуса вдоль y была такой, чтобы за время Tп корпус достигал критического положения (максимальное отклонение по y, при нулевой скорости вдоль y). Тогда, благодаря симметрии принятого движения в конце шага, корпус снова окажется в среднем положении и с той же скоростью, но направленной в другую сторону. Для расчёта необходимой начальной (из среднего положения) скорости вдоль y примем, что в начальный момент времени t=0 корпус находится в критическом положении, а y отсчитывается от опорной стопы (рис. 2).
Положение корпуса по y в критической точке
 .
.
Скорость, спустя время Tп
![]() .
.
 |
Рис. 2. Критическое положение корпуса во фронтальной плоскости
Знак, вычисленной таким образом начальной скорости, принимается в зависимости от того, какая нога опорная. Скорость должна быть направлена к опорной стопе.
Полученные выше соотношения позволяют сформировать управление на основном шаге, а также сформулировать задачу на стартовом шаге. На стартовом шаге из состояния покоя, когда корпус находится над опорной стопой, необходимо начать движение и сформировать его таким образом, чтобы к концу одноопорной фазы стартового шага (в момент времени Tc) опорная стопа достигла положения xcc=xc2=xc1 с нулевой скоростью (vcc=0), а корпус пришел в положение xkc=xk1 со скоростью vkc=vk1.
Управление движением на стартовом шаге реализуем, выбирая подходящую зависимость координаты переносимой стопы от времени (рис. 3). Сначала запишем уравнение движения корпуса, если движение стопы – известная функция времени. Для этого используем первое уравнение из системы, полученной для свободного движения робота в одноопорной фазе
![]() ,
,
в котором коэффициенты имеют прежние значения. Соответствующее однородное уравнение имеет вид
![]() .
.
 |
Рис. 3. Зависимость y(t) на стартовом шаге
Его характеристическое уравнение имеет два корня. Обозначим их l2 и -l2. Здесь, как и прежде
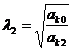 .
.
Зависимость движения переносимой стопы от времени назначим в следующем виде:

В процессе движения реального робота это движение будет обеспечиваться приводами в следящем по положению режиме.
Граничные условия:
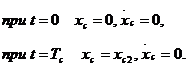
Для обеспечения требуемых параметров движения в конце стартового шага будем варьировать Tc и C2, а C1 и С3 определим из граничных условий
Введем параметр
![]() .
.
и запишем уравнения движения корпуса в следующем виде:
 ,
,
где

Далее для формирования управления роботом необходимо найти такие Kн и Tc , чтобы выполнялись условия

Для численного решения этой задачи используем следующие зависимости: 

где

Для расчёта положения и скорости корпуса в реальном времени удобно использовать следующие выражения

в которых постоянные на шаге коэффициенты равны

К концу стартового шага (к моменту времени Tc+T2) необходимо, чтобы во фронтальной плоскости корпус развил скорость y'кп. Один из возможных вариантов достичь этого следующий. Разгон до необходимой скорости производится от положения y0 относительно опорной стопы ровно по тому же закону, что и на основном шаге. В исходном положении робот стоит на двух ногах, корпус робота расположен посередине. Из этого положения корпус должен достичь положения y0 с нулевой скоростью, причем время, не меньшее Tc-T1, он должен двигаться, опираясь на ногу, которая является опорной в фазе разгона в сагиттальной плоскости. Значит время tторм, большее, чем Tc-T1 он должен тормозить по обратному закону, а отрезок времени ty-2…ty-1 - разгоняться на другой ноге из исходного положения. Таким образом, необходимо отыскать положение корпуса, при котором необходимо сменить опорную ногу, и соответствующий момент времени ty-1. Для этого воспользуемся свойством непрерывности скорости.
Определим зависимость скорости от коррдинаты при следующих условиях:
- начальная скорость корпуса равна нулю,
- координата корпуса отн. опорной точки равна y0,
- на всем интервале скорость переносимой стопы равна нулю,
- расстояние от переносимой стопы до опорной точки равно B.
Тогда

Подставив в полученное соотношение в качестве начального условия y0 и B/2, получим два варианта его правой части, приравняв которые, получим уравнение. Его решение и есть искомая точка переключения yп, измеренная относительно опорной стопы. Решать это уравнение будем численно. Зная yп, по следующей формуле найдем момент времени, в который надо производить переключение

(время отсчитано от момента ty-2).
Полученные выше соотношения, приближённо описывают один из множества возможных способов движения ДШР в режиме динамической ходьбы. Получены они, исходя из условия нулевых шарнирных моментов, что обеспечивает минимизацию мощности, расходуемой на движение реального робота. Однако, их не целесообразно использовать при больших углах отклонения ног от вертикали (по оценкам авторов – не более 200). Данные соотношения не могут быть использованы для управления роботом непосредственно, так как не учитывают множества факторов (например, удары, вертикальные движения стоп, изгиб ног в коленях). Однако, они могут быть использованы в качестве "отправной точки" для синтеза реальных реализуемых роботом законов управления, что было с успехом проделано авторами применительно к лабораторному образцу ДШР, разрабатываемому на каф. Э-10 совместно с МИПК МГТУ им. Н.Э.Баумана (Рис.4). Исполнительный механизм робота имеет 12 управляемых степеней подвижности, электрогидравлический следящий привод, рост 2,2 м и массу 200 кг. Приведённые в программном обеспечении системы управления роботом зависимости, аппроксимируются достаточно простыми функциями с малым числом параметров - отрезками прямых и синусоид. Затем, полученные кривые, оптимизируются по небольшому числу параметров, с


Рис. 4. Лабораторный ДШР; вид спереди и сзади
целью минимизации динамических возмущений, возникающих в процессе ходьбы. Далее спроектированное таким способом движение отрабатывается реальным многостепенным исполнительным механизмом робота и реализуется его динамическая ходьба по ровной горизонтальной поверхности.
Список литературы
1. Белецкий В.В. Двуногая ходьба. М.: Наука, 1984. 287 с.
2. Вукобратович М. Шагающие роботы и антропоморфные механизмы. М.: Мир, 1976. 541 с.
3. Ковальчук А.К., Семёнов С.Е. Кинематический алгоритм управления движением двуногого шагающего робота // Вестник МГТУ им. Н.Э.Баумана. Приборостроение. М.: Изд-во МГТУ им. Н.Э.Баумана, 1996. ╧ 1. С.57-69.
4. Ковальчук А.К., Кулаков Д.Б., Семёнов С.Е.. Принципы построения программного обеспечения системы управления антропоморфным шагающим роботом // Автоматизация и современные технологии. М.: Машиностроение, 2007. ╧ 2.
5. Ковальчук А.К., Кулаков Д.Б., Семёнов С.Е., Горина Г.Ю. История и развитие антропоморфных шагающих роботов – как нового класса робототехнических средств для экстремальных условий // Наука и образование: электронное научно-техническое издание. М., 2006. ╧ 12.
6. Ковальчук А.К., Кулаков Д.Б., Семёнов С.Е. Математическое описание кинематики и динамики исполнительных механизмов роботов с древовидной кинематической структурой // Известия вузов. Машиностроение. М., 2008. ╧ 11. С.13-25.
7. Ковальчук А.К., Кулаков Д.Б., Семёнов С.Е. Блочно-матричные уравнения движения исполнительных механизмов роботов с древовидной кинематической структурой // Известия вузов. Машиностроение. М., 2008. ╧ 12. С.5-21.
Публикации с ключевыми словами: автономный электрогидравлический следящий привод, шагающий робот
Публикации со словами: автономный электрогидравлический следящий привод, шагающий робот
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



