научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 01, январь 2010
DOI: 10.7463/0110.0135944
УДК 519.6
МГТУ им. Н.Э.Баумана, 105005, Москва, 2-я Бауманская ул., д.5.,
karpenko@nog.ru
dimidia@mail.ru
Введение
Во многих приложениях, использующих модели исследуемых объектов в виде обыкновенных дифференциальных уравнений (ОДУ), возникает задача построения области достижимости соответствующей динамической системы. Например, такая задача возникает при решении проблемы траекторной безопасности летального аппарата [1], при решении близкой задачи о посадке вертолета на подвижный носитель [2]. Важной особенностью задачи построения области достижимости является то, что ее часто приходится решать в режиме реального времени.
Аналитическое построение области достижимости удается лишь в простейших случаях, не представляющих практического интереса. Поэтому для построения этой области приходится использовать численные методы.
Дискретную аппроксимацию области достижимости динамической системы можно построить путем многократного интегрирования модельной системы ОДУ при различных управлениях (метод мультифиниша). В практических задачах типичной является ситуация, когда основные вычислительные затраты при построении области достижимости этим методом обусловлены затратами на интегрирование указанной системы ОДУ. Поэтому ускорить вычисления можно за счет параллельного интегрирования этой системы ОДУ.
К параллельным методам интегрирования ОДУ относятся блочные методы, а также методы на основе геометрической схемы декомпозиции системы ОДУ.
Методы первого класса основаны на использовании одношаговых и многошаговых блочных формул интегрирования ОДУ, например, формулы Адамса-Башфорта [3]. В вычислительной практике обычно используются не более чем 4-х точечные блочные методы. Поэтому потенциальный параллелизм этой группы методов невелик.
Идея методов второго класса состоит в разбиении модельной системы ОДУ на подсистемы, количество которых равно количеству используемых процессоров вычислительной системы, и интегрировании каждой из подсистем на своем процессоре. В силу, как правило, относительно невысокой размерности вектора фазовых координат исследуемой динамической системы, данные методы также принципиально не могут обеспечить значительное ускорение.
Если не оговорено противное, в работе полагается, что, используемая многопроцессорная вычислительная система (МВС) представляет собой однородную MIMD-систему с общей или распределенной памятью [4]. Поскольку метод мультифиниша использует интегрирование совокупности систем модельных ОДУ, естественным в данном случае является распараллеливание на основе разделения этой совокупности на наборы, количество которых равно количеству процессоров в используемой МВС. В работе рассматривается проблема балансировки загрузки МВС при распараллеливании метода мультифинаша по указанной схеме, получены оценки эффективности параллельных вычислений.
Даже при вычислениях на однопроцессорной ЭВМ значительное ускорение при построении области достижимости можно обеспечить на основе аппроксимации векторного поля модельной системы ОДУ [2]. При этом область допустимых значений вектор-функции, соответствующей правым частям системы ОДУ, покрывается некоторой сеткой. Предварительно во всех узлах этой сетки вычисляются значения указанной вектор-функции и сохраняются в оперативной памяти ЭВМ. При интегрировании модельной системы ОДУ используются эти значения или их подходящая аппроксимация. В работе получены оценки объема требуемой оперативной памяти, а также оценки ускорения данного метода.
Очевидной является идея использовать метод мультифиниша с заменой модельной системы ОДУ ее некоторой нейросетевой аппроксимацией. Поскольку диапазон начальных условий рассматриваемой динамической системы и ее управлений могут быть весьма широки, для обеспечения требуемой точности аппроксимации в данном случае может оказаться необходимым использование нескольких нейронных сетей. Кроме того, данный метод не дает кардинального сокращения времени построения области достижимости. Указанные обстоятельства не позволяют считать перспективным метод построения области достижимости на основе нейросетевой аппроксимации исследуемой динамической системы, и этот метод не рассматривается в работе.
В работе используется другой подход к построению области достижимости с использованием нейронных сетей – подход, основанный на построении нейронной сети, выходами которой являются непосредственно координаты точек, принадлежащие области достижимости или ее границе.
В качестве примера рассмотрена задача построения области достижимости для летального аппарата, описываемого системой ОДУ шестого порядка. Рассмотрено решение задачи с помощью метода мультифиниша, метода аппроксимации векторного поля этой системы ОДУ, а также нейросетевого метода.
В разделе 1 дана постановка задачи, в разделе 2 рассмотрены методы мультифиниша, в разделе 3 – методы на основе аппроксимации векторного поля, в разделе 4 – нейросетевые методы. Раздел 5 содержит пример использования указанных методов для построения границы области достижимости летального аппарата. В заключении сформулированы основные выводы.
1. Постановка задачи
Рассмотрим динамическую систему
 (1)
(1)
где ![]() - n-мерный вектор фазовых переменных системы,
- n-мерный вектор фазовых переменных системы, ![]() - m-мерный вектор управлений,
- m-мерный вектор управлений, ![]() - n-мерный вектор начальных условий,
- n-мерный вектор начальных условий, ![]() . На вектор фазовых переменных
. На вектор фазовых переменных ![]() и вектор управления
и вектор управления ![]() наложены ограничения
наложены ограничения
![]() ,
, ![]() , (2)
, (2)
где ![]() - некоторое пространство m-мерных функций, определенных на интервале
- некоторое пространство m-мерных функций, определенных на интервале ![]() , например, пространство функций, интегрируемых с квадратом на этом интервале.
, например, пространство функций, интегрируемых с квадратом на этом интервале.
Для компактности записи используем векторную форму системы (1)
![]() ,
, ![]() , (3)
, (3)
где ![]() - n-мерная вектор-функция.
- n-мерная вектор-функция.
Среди фазовых переменных ![]() выделим
выделим ![]() переменных. Не ограничивая общности, положим, что эти переменные образуют
переменных. Не ограничивая общности, положим, что эти переменные образуют ![]() -мерный вектор
-мерный вектор
![]() .
.
Областью достижимости ![]() системы (3) назовем множество всех возможных значений вектора
системы (3) назовем множество всех возможных значений вектора ![]() , которые принимаются на решениях системы (3) при начальных условиях
, которые принимаются на решениях системы (3) при начальных условиях ![]() и выполнении ограничений (2).
и выполнении ограничений (2).
Ставим следующую прямую задачу: при заданном векторе начальных условий ![]() и конечном времени
и конечном времени ![]() построить область достижимости
построить область достижимости ![]() системы (3). Рассмотрим также обратную задачу: при заданных векторе начальных условий
системы (3). Рассмотрим также обратную задачу: при заданных векторе начальных условий ![]() , конечном времени
, конечном времени ![]() и точке
и точке ![]() , принадлежащей области достижимости
, принадлежащей области достижимости ![]() , найти управление
, найти управление ![]() , переводящее систему (3) в эту точку.
, переводящее систему (3) в эту точку.
Для решения прямой задачи, очевидно, достаточно построить границу ![]() области достижимости
области достижимости ![]() . В некоторых случаях удается найти множество допустимых управлений
. В некоторых случаях удается найти множество допустимых управлений ![]() , принадлежащих классу управлений
, принадлежащих классу управлений ![]() , которые приводят систему (3) на эту границу [1]. В этом случае прямая задача сводится к построению границы
, которые приводят систему (3) на эту границу [1]. В этом случае прямая задача сводится к построению границы ![]() .
.
Сделаем следующие допущения. Во всех случаях при интегрировании системы ОДУ (3) используется алгоритм с постоянным шагом интегрирования ![]() , где
, где ![]() - количество шагов интегрирования. Каждый из шагов интегрирования требуется
- количество шагов интегрирования. Каждый из шагов интегрирования требуется ![]() вычислений значения функции
вычислений значения функции ![]() , вычислительная сложность которой (количество арифметических операций, необходимых для однократного вычисления значения этой функции) не зависит от аргументов
, вычислительная сложность которой (количество арифметических операций, необходимых для однократного вычисления значения этой функции) не зависит от аргументов ![]() и равна
и равна ![]() . Вычислительная сложность затрат на реализацию алгоритма интегрирования на одном шаге интегрирования равна
. Вычислительная сложность затрат на реализацию алгоритма интегрирования на одном шаге интегрирования равна ![]() .
.
2. Методы мультифиниша
2.1. Схема методов. Покроем множество ![]() некоторой сеткой с узлами
некоторой сеткой с узлами ![]() , где
, где ![]() - общее количество узлов сетки. Поставим в соответствие системе (3) совокупность
- общее количество узлов сетки. Поставим в соответствие системе (3) совокупность ![]() систем ОДУ с указанными управлениями:
систем ОДУ с указанными управлениями:
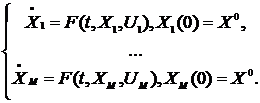 (4)
(4)
Тогда схему приближенного решения прямой задачи методами мультифиниша можно представить в следующем виде.
1) Путем интегрирования совокупности систем ОДУ (4) находим множество точек ![]() , представляющее собой дискретную аппроксимацию области
, представляющее собой дискретную аппроксимацию области ![]() .
.
2) Запоминаем полученные наборы значений ![]() ,
, ![]() .
.
3) Во множестве ![]() находим граничные точки
находим граничные точки ![]() , представляющие собой дискретную аппроксимацию границы
, представляющие собой дискретную аппроксимацию границы ![]() области достижимости.
области достижимости.
4) Запоминаем соответствующие наборы значений ![]() ,
, ![]() .
.
5) На основе точек ![]() строим подходящую непрерывную аппроксимацию
строим подходящую непрерывную аппроксимацию ![]() границы
границы ![]() .
.
Задача построения дискретной или непрерывной аппроксимации границы ![]() представляет собой классическую задачу вычислительной геометрии – задачу построения оболочки облака точек. Методы решения этой задачи хорошо разработаны (см., например, [5]), известно значительное количество программных систем, реализующих такие методы (см., например, [6]). Поэтому в данной работе рассматривается только шаг 1, приведенной схемы приближенного решения прямой задачи.
представляет собой классическую задачу вычислительной геометрии – задачу построения оболочки облака точек. Методы решения этой задачи хорошо разработаны (см., например, [5]), известно значительное количество программных систем, реализующих такие методы (см., например, [6]). Поэтому в данной работе рассматривается только шаг 1, приведенной схемы приближенного решения прямой задачи.
Обратная задача в методах мультифиниша может быть решена по следующей схеме.
1) Во множестве точек ![]() находим точку
находим точку ![]() , которая является в используемой метрике ближайшей к заданной точке
, которая является в используемой метрике ближайшей к заданной точке ![]() .
.
2) В качестве искомого управления принимаем управление, соответствующее точке ![]() .
.
2.2. Схема распараллеливания вычислений имеет следующий вид:
1) процессор ![]() ,
, ![]() получает от
получает от ![]() - процессора векторы
- процессора векторы ![]() ;
;
2) интегрирует при этих управлениях систему ОДУ (3) - находит множество точек ![]() ;
;
3) передает координаты этих точек ![]() - процессору.
- процессору.
Здесь ![]() - количество процессоров в используемой МВС;
- количество процессоров в используемой МВС;  ,где
,где ![]() - символ ближайшего целого большего v.
- символ ближайшего целого большего v.
При параллельном построении множества достижимости по указанной схеме в допущениях раздела 1 проблема балансировки загрузки МВС не возникает. При построении границы ![]() области достижимости
области достижимости ![]() ситуация может быть иной. Рассмотрим для примера случай, когда класс функций
ситуация может быть иной. Рассмотрим для примера случай, когда класс функций ![]() представляет собой класс релейных функций с не более чем одной точкой переключения. Положим, что одна из границ множества достижимости формируется управлениями этого класса, в которых все компоненты вектора управления, кроме одного, постоянны, а один из компонентов имеет одну точку переключения. Пусть, например,
представляет собой класс релейных функций с не более чем одной точкой переключения. Положим, что одна из границ множества достижимости формируется управлениями этого класса, в которых все компоненты вектора управления, кроме одного, постоянны, а один из компонентов имеет одну точку переключения. Пусть, например,

![]()
где ![]() - момент времени, когда происходит переключение управления
- момент времени, когда происходит переключение управления ![]() [1].
[1].
2.3. Равномерная декомпозиция точек переключения. Покроем интервал ![]() равномерной сеткой с шагом
равномерной сеткой с шагом ![]() и узлами
и узлами ![]() ,
, ![]() . Положим, что шаг
. Положим, что шаг ![]() кратен шагу
кратен шагу ![]() , так что
, так что ![]() , где
, где ![]() - целое число. При этом множество управлений
- целое число. При этом множество управлений ![]() естественно сформировать в виде
естественно сформировать в виде
![]() ,
, ![]() .
.
Таким образом, схема распараллеливания имеет вид, представленный на рисунке 1.

Рис. 1. Схема распараллеливания при равномерной декомпозиции точек переключения
В соответствии с этой схемой на процессоре ![]() выполняется интегрирование системы ОДУ (3) при управлениях
выполняется интегрирование системы ОДУ (3) при управлениях ![]() , на процессоре
, на процессоре ![]() - при управлениях
- при управлениях ![]() и т.д. до процессора
и т.д. до процессора ![]() , который выполняет интегрирование при управлениях
, который выполняет интегрирование при управлениях ![]() .
.
Вычисления на процессоре ![]() организуем следующим образом.
организуем следующим образом.
Шаг 0 (этап «разгона»). Исходя из начальных условий ![]() , выполняем интегрирование системы (3) при управлении
, выполняем интегрирование системы (3) при управлении ![]() от момента времени
от момента времени ![]() до момента времени
до момента времени ![]() и запоминает значения компонентов векторов
и запоминает значения компонентов векторов ![]() ,
, ![]() ,…,
,…, ![]() .
.
Шаг 1. Исходя из начальных условий ![]() , выполняем интегрирование системы (3) при управлении
, выполняем интегрирование системы (3) при управлении ![]() от момента времени
от момента времени ![]() до момента времени
до момента времени ![]() .
.
Шаг 2. Исходя из начальных условий ![]() , выполняем интегрирование системы (3) при управлении
, выполняем интегрирование системы (3) при управлении ![]() от момента времени
от момента времени ![]() до момента времени
до момента времени ![]() .
.
· …
Шаг ![]() . Исходя из начальных условий
. Исходя из начальных условий ![]() , выполняем интегрирование системы (3) при управлении
, выполняем интегрирование системы (3) при управлении ![]() от момента времени
от момента времени ![]() до момента времени
до момента времени ![]() .
.
Замечание. В рассмотренной схеме каждый из последующих процессоров повторяет шаг 0 своего предыдущего процессора и только затем выполняет интегрирование системы (3) на «своем» интервале ![]() . Если вычислительные затраты на интегрирование системы (3) велики, то может оказаться целесообразной более «тонкая» организация вычислений на этапе разгона – однократное интегрирование системы (3) на интервале
. Если вычислительные затраты на интегрирование системы (3) велики, то может оказаться целесообразной более «тонкая» организация вычислений на этапе разгона – однократное интегрирование системы (3) на интервале ![]() при управлении
при управлении ![]() на одном процессоре и передача значений необходимых компонентов векторов
на одном процессоре и передача значений необходимых компонентов векторов ![]() ,
, ![]() ,…,
,…,![]() остальным процессорам вычислительной системы. Однако, если
остальным процессорам вычислительной системы. Однако, если ![]() , что можно считать типичной ситуацией, выигрыш от такой организации вычислений не может быть существенным.
, что можно считать типичной ситуацией, выигрыш от такой организации вычислений не может быть существенным.
Оценим ускорение рассмотренной схемы распараллеливания. В сделанных допущениях время выполнения процессором ![]() этапа «разгона» равно
этапа «разгона» равно
![]() ; (5)
; (5)
время выполнения j-го шага, где ![]() , можно оценить величиной
, можно оценить величиной
![]() . (6)
. (6)
Таким образом, общее время решения задачи процессором ![]() равно
равно
![]() . (7)
. (7)
Здесь и далее ![]() - время выполнения арифметической операции на одном процессоре используемой МВС.
- время выполнения арифметической операции на одном процессоре используемой МВС.
Поскольку загрузка первого процессора ![]() в данном случае, очевидно, максимальна, время параллельного решения задачи определяется выражением
в данном случае, очевидно, максимальна, время параллельного решения задачи определяется выражением
![]() =
=![]()
![]() ,
,
где учтено, что ![]() . Аналогично, время последовательного решения задачи на одном процессоре оценим величиной
. Аналогично, время последовательного решения задачи на одном процессоре оценим величиной
![]()
![]() .
.
Отсюда имеем
Утверждение 1. Ускорение ![]() параллельного метода на основе равномерной декомпозиции точек переключения управления
параллельного метода на основе равномерной декомпозиции точек переключения управления ![]() оценивается величиной
оценивается величиной
![]() .
.
Из утверждения 1 следует, что равномерная декомпозиция точек переключения управления ![]() не может обеспечить ускорение, превышающее 50% от максимального потенциально возможного ускорения, равного
не может обеспечить ускорение, превышающее 50% от максимального потенциально возможного ускорения, равного ![]() .
.
Лучшей балансировки загрузки многопроцессорной вычислительной системы можно добиться за счет неравномерной декомпозиции точек переключения управления ![]() .
.
2.4. Неравномерная декомпозиция точек переключения. Положим, что процессор ![]() выполняется интегрирование системы ОДУ (3) при управлениях
выполняется интегрирование системы ОДУ (3) при управлениях ![]() , а процессор
, а процессор ![]() - при управлениях
- при управлениях ![]() ,
, ![]() . Потребуем, чтобы времена решения задачи процессорами
. Потребуем, чтобы времена решения задачи процессорами ![]() ,
, ![]() были равны, т.е. чтобы выполнялось равенство
были равны, т.е. чтобы выполнялось равенство ![]() ,
, ![]() . Из выражений (5) – (7) следует, что для этого необходимо выполнение равенства
. Из выражений (5) – (7) следует, что для этого необходимо выполнение равенства
![]() =
=![]()
или, что то же самое, равенства
![]() . (8)
. (8)
Отсюда вытекает квадратное уравнение для определения величины ![]()
![]() при известных значениях величин
при известных значениях величин ![]() :
:
![]() . (9)
. (9)
Если для процессора ![]() задаться величинами
задаться величинами ![]() ,
, ![]() , то из выражения (9) легко найти последовательно управления, которые должны обрабатывать процессоры
, то из выражения (9) легко найти последовательно управления, которые должны обрабатывать процессоры ![]()
Рассмотрим для примера случай ![]() ,
, ![]() . Из (9) вытекает, что в данном случае можно обеспечить загрузку 6 процессоров (таблица 1). Отметим, что здесь количество точек переключения
. Из (9) вытекает, что в данном случае можно обеспечить загрузку 6 процессоров (таблица 1). Отметим, что здесь количество точек переключения ![]() вычислено по остаточному принципу и не удовлетворяет уравнению (9).
вычислено по остаточному принципу и не удовлетворяет уравнению (9).
Таблица 1. Пример неравномерной декомпозиции точек переключения
Процессор |
|
|
|
| 0 | 100 | 100 |
| 101 | 212 | 111 |
| 213 | 342 | 129 |
| 343 | 504 | 151 |
| 505 | 756 | 251 |
| 757 | 1000 | 243 |
Оценим ускорение рассматриваемого метода. Положим, что в последовательном режиме задача решается по схеме, аналогичной рассмотренной выше (с этапом «разгона»). Тогда время последовательного решения задачи можно оценить величиной
![]()
![]() .
.
Поскольку в данном случае вычислительная загрузка всех используемых процессоров (исключая, быть может, последний процессор) примерно одинакова, оценка времени параллельного решения задачи следует из выражения (8) и равна
![]() =
=![]() .
.
Таким образом, имеем
Утверждение 2. Ускорение ![]() параллельного метода на основе неравномерной декомпозиции точек переключения управления
параллельного метода на основе неравномерной декомпозиции точек переключения управления ![]() оценивается величиной
оценивается величиной
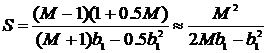 .
.
Из утверждения 2 следует, что для рассмотренного выше примера ускорение равно
![]() .
.
Заметное отличие ускорения от максимально возможного (равного 6) объясняется тем, что загрузка последнего процессора ![]() далека от оптимальной загрузки.
далека от оптимальной загрузки.
Рассмотрим другой пример. Пусть ![]() . Тогда по формуле (9) получим
. Тогда по формуле (9) получим ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Поскольку при этом все шесть процессоров загружены практически равномерно, ускорение равно
. Поскольку при этом все шесть процессоров загружены практически равномерно, ускорение равно
![]() .
.
Явное решение рекуррентного уравнения (8) не удается. Поэтому количество точек переключения ![]() , обрабатываемых процессором
, обрабатываемых процессором ![]() , приходится подбирать таким образом, чтобы вычислительная загрузка всех процессоров, включая последний процессор, была примерно одинакова. При этом критерий окончания перебора удобно строить, исходя из того, что при несбалансированности загрузки процессора
, приходится подбирать таким образом, чтобы вычислительная загрузка всех процессоров, включая последний процессор, была примерно одинакова. При этом критерий окончания перебора удобно строить, исходя из того, что при несбалансированности загрузки процессора ![]() корни уравнения (9) оказываются комплексными.
корни уравнения (9) оказываются комплексными.
3. Методы на основе аппроксимации векторного поля системы ОДУ
3.1. Схема методов. Идея методов этой группы состоит в следующем.
1). Предварительно множество ![]() покрываем некоторой сеткой
покрываем некоторой сеткой ![]() с узлами
с узлами ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
2). Предварительно во всех узлах указанной сетки вычисляем значения функции ![]() и запомним эти значения.
и запомним эти значения.
3). Поочередно для ![]() тем или иным методом численно интегрируем систему ОДУ (3) при управлении
тем или иным методом численно интегрируем систему ОДУ (3) при управлении ![]() , используя в качестве требуемых значений функции
, используя в качестве требуемых значений функции ![]() соответствующие интерполяции или аппроксимации запомненных значений этой функции.
соответствующие интерполяции или аппроксимации запомненных значений этой функции.
Ускорение вычислений в методах данного класса достигается из-за того, что этапы 1, 2 выполняются предварительно, а при выполнении этапа 3 не требуется вычислять значения правых частей системы ОДУ (3).
Для того чтобы использовать весь потенциал данных методов значения функции ![]() в узлах сетки
в узлах сетки ![]() следует хранить в оперативной памяти компьютера. Примем, что длина вещественного числа равна 4 байтам. Тогда с учетом того факта, что общее количество узлов сетки
следует хранить в оперативной памяти компьютера. Примем, что длина вещественного числа равна 4 байтам. Тогда с учетом того факта, что общее количество узлов сетки ![]() равно
равно ![]() , имеем
, имеем
Утверждение 3. Требуемый объем памяти для хранения значений функции ![]() в узлах сетки
в узлах сетки ![]() равен
равен
![]() байт.
байт.
Из утверждения 3 следует, что если, например, ![]() ,
, ![]() ,
, ![]() , то
, то ![]() байт
байт![]() 20 Гбайт.
20 Гбайт.
3.2. Кусочно-постоянная интерполяция функции ![]() . Рассмотрим прежде случай, когда в качестве значения
. Рассмотрим прежде случай, когда в качестве значения ![]() используется значение этой функции в ближайшем узле сетки
используется значение этой функции в ближайшем узле сетки ![]() . Такая схема вычислений применима при построении области
. Такая схема вычислений применима при построении области ![]() в грубом приближении и означает использование кусочно-постоянной интерполяции функции
в грубом приближении и означает использование кусочно-постоянной интерполяции функции ![]() .
.
Оценим ускорение, которое обеспечивает метод в этом случае. Вычислительные затраты при численном интегрировании ОДУ состоят из затрат на вычисление значений функции ![]() и затрат на реализацию собственно используемого алгоритма интегрирования. В допущениях раздела 1 время приближенного построения области
и затрат на реализацию собственно используемого алгоритма интегрирования. В допущениях раздела 1 время приближенного построения области ![]() путем интегрирования системы ОДУ (3) без предварительного вычисления значений функции
путем интегрирования системы ОДУ (3) без предварительного вычисления значений функции ![]() может быть оценено величиной
может быть оценено величиной ![]() . Это же время при кусочно-постоянной интерполяции функции
. Это же время при кусочно-постоянной интерполяции функции ![]() оценивается величиной
оценивается величиной ![]() . Таким образом, имеет место
. Таким образом, имеет место
Утверждение 4. Ускорение ![]() последовательного метода на основе кусочно-постоянной интерполяции функции
последовательного метода на основе кусочно-постоянной интерполяции функции ![]() равно
равно
 . (10)
. (10)
Поскольку обычно ![]() , из утверждения 4 следует, что ускорение в данном случае можно принять равным
, из утверждения 4 следует, что ускорение в данном случае можно принять равным  .
.
Заметим, что оценка (10) получена в предположении, что при интегрировании системы ОДУ (3), как без предварительного вычисления значений функции ![]() , так и с таким вычислением, применяется один и тот же метод интегрирования и с одним и тем же шагом интегрирования. Вообще говоря, из соображений обеспечения заданной точности приближенного построения области
, так и с таким вычислением, применяется один и тот же метод интегрирования и с одним и тем же шагом интегрирования. Вообще говоря, из соображений обеспечения заданной точности приближенного построения области ![]() , в первом случае можно было бы использовать больший шаг интегрирования. Однако аналитические оценки величины этого шага не удаются.
, в первом случае можно было бы использовать больший шаг интегрирования. Однако аналитические оценки величины этого шага не удаются.
3.3. Кусочно-линейная интерполяция функции ![]() . При том же количестве узлов сетки
. При том же количестве узлов сетки ![]() большую точность вычислений можно обеспечить путем использования линейной интерполяции функции
большую точность вычислений можно обеспечить путем использования линейной интерполяции функции ![]() на узлах этой сетки. При этом рассмотренная выше идея последовательных методов существенно изменяется. Дело в том, что построение интерполирующей функции, даже в том случае, когда она является линейной, требует значительных вычислительных затрат. Поэтому в данном случае целесообразно хранить не значения функции
на узлах этой сетки. При этом рассмотренная выше идея последовательных методов существенно изменяется. Дело в том, что построение интерполирующей функции, даже в том случае, когда она является линейной, требует значительных вычислительных затрат. Поэтому в данном случае целесообразно хранить не значения функции ![]() в узлах сетки
в узлах сетки ![]() , а заранее строить интерполирующие функции для каждой из ячеек этой сетки и хранить коэффициенты этих функций.
, а заранее строить интерполирующие функции для каждой из ячеек этой сетки и хранить коэффициенты этих функций.
В ячейке ![]() сетки
сетки ![]() , ограниченной узлами
, ограниченной узлами ![]() ,
, ![]() ,
, ![]() ,
,![]() построим линейную интерполирующую функцию
построим линейную интерполирующую функцию
![]() ,
,
(11)
где ![]() -
- ![]() -вектор неизвестных коэффициентов,
-вектор неизвестных коэффициентов, ![]() - такой же вектор аргументов функции
- такой же вектор аргументов функции ![]() ,
, ![]() - символ скалярного произведения векторов. Коэффициенты
- символ скалярного произведения векторов. Коэффициенты ![]() при этом находятся из системы линейных алгебраических уравнений (СЛАУ)
при этом находятся из системы линейных алгебраических уравнений (СЛАУ)
 (12)
(12)
где ![]() ,
, ![]() - узлы ячейки
- узлы ячейки ![]() . Отметим, что общее количество узлов ячейки
. Отметим, что общее количество узлов ячейки ![]() равно, очевидно,
равно, очевидно, ![]() .
.
Утверждение 5. Объем памяти, необходимый для хранения коэффициентов ![]() линейной интерполяции функции
линейной интерполяции функции ![]() на сетке
на сетке ![]() , равен
, равен
![]() байт.
байт.
Из утверждения 5 следует, что если, например, ![]() ,
, ![]() ,
, ![]() , то
, то ![]() байт
байт![]()
![]() 16 Гбайт.
16 Гбайт.
Ускорение последовательного метода на основе кусочно-линейной интерполяции функции ![]() определяется так же, как в методе на основе кусочно-постоянной интерполяции - см. выражение (10).
определяется так же, как в методе на основе кусочно-постоянной интерполяции - см. выражение (10).
Отметим, что функция ![]() в общем случае не является непрерывной.
в общем случае не является непрерывной.
3.4. Кусочно-линейная аппроксимация функции ![]() . Известной проблемой интерполяции многомерных функций является проблема невозможности использования произвольных сеток. Так для двумерной функции и интерполяции по трем узлам, для обеспечения невырожденности системы (12) эти узлы не могут быть расположены на одной прямой. Аналогично, при интерполяции той же функции по шести узлам, эти узлы не могут быть расположены на одной кривой второго порядка и т.д. Поэтому в вычислительной практике при построении множества
. Известной проблемой интерполяции многомерных функций является проблема невозможности использования произвольных сеток. Так для двумерной функции и интерполяции по трем узлам, для обеспечения невырожденности системы (12) эти узлы не могут быть расположены на одной прямой. Аналогично, при интерполяции той же функции по шести узлам, эти узлы не могут быть расположены на одной кривой второго порядка и т.д. Поэтому в вычислительной практике при построении множества ![]() целесообразно использовать не интерполяцию функции
целесообразно использовать не интерполяцию функции ![]() , а ее аппроксимацию на основе метода наименьших квадратов (МНК).
, а ее аппроксимацию на основе метода наименьших квадратов (МНК).
Для кусочно-линейной аппроксимирующей функции в этом случае имеем следующую СЛАУ относительно неизвестных коэффициентов ![]() :
:

В соответствии с методикой МНК, решение этой системы имеет вид
![]() , (13)
, (13)
где ![]() -векторы и
-векторы и ![]() -матрица равны, соответственно,
-матрица равны, соответственно,
![]() ,
, ![]() ;
; ![]() ;
;
![]() . Важно, что кроме вырожденного случая, когда все точки
. Важно, что кроме вырожденного случая, когда все точки ![]() лежат в одной плоскости, решение СЛАУ (13) существует и единственно.
лежат в одной плоскости, решение СЛАУ (13) существует и единственно.
Объем памяти, необходимый для хранения коэффициентов ![]() кусочно-линейной аппроксимации функции
кусочно-линейной аппроксимации функции ![]() на сетке
на сетке ![]() , определяется утверждением 5. Ускорение последовательного метода на основе кусочно-линейной аппроксимации функции
, определяется утверждением 5. Ускорение последовательного метода на основе кусочно-линейной аппроксимации функции ![]() определяется утверждением 4.
определяется утверждением 4.
Отметим, что, как и в предыдущем пункте, функция ![]() , вообще говоря, не является непрерывной.
, вообще говоря, не является непрерывной.
3.5. Другие методы аппроксимация функции ![]() . Большое количество вариантов рассмотренного в предыдущем пункте подхода к кусочно-линейной аппроксимации функции
. Большое количество вариантов рассмотренного в предыдущем пункте подхода к кусочно-линейной аппроксимации функции ![]() , можно получить с привлечением результатов теории планирования эксперимента. Так каждый из узлов сетки
, можно получить с привлечением результатов теории планирования эксперимента. Так каждый из узлов сетки ![]() можно использовать в качестве центральной точки для построения регрессионного плана эксперимента первого порядка, удовлетворяющего критерию D-оптимальности, А-оптимальности, E- оптимальности и т.д. [7]. СЛАУ (13) при этом сохраняет свою структуру.
можно использовать в качестве центральной точки для построения регрессионного плана эксперимента первого порядка, удовлетворяющего критерию D-оптимальности, А-оптимальности, E- оптимальности и т.д. [7]. СЛАУ (13) при этом сохраняет свою структуру.
Повысить точность аппроксимации функции ![]() можно за счет использования в пределах каждой из ячеек
можно за счет использования в пределах каждой из ячеек ![]() квадратичной аппроксимации. При этом естественно ориентироваться на планы эксперимента второго порядка такие, как центрально-композиционные планы, композиционные планы Хартли и Вестлейка [8].
квадратичной аппроксимации. При этом естественно ориентироваться на планы эксперимента второго порядка такие, как центрально-композиционные планы, композиционные планы Хартли и Вестлейка [8].
В алгоритмическом отношении для аппроксимации удобно использовать композицию одномерных полиномов (метод Брандона) [9].
3.6. Распараллеливание вычислений.Дальнейшего уменьшения времени решения задачи можно добиться путем организации параллельных вычислений. Схема распараллеливания при этом не отличается от схемы, рассмотренной в п. 2.4.
4. Нейросетевые методы
Для аппроксимации многомерных функций чаще всего используют многослойные нейронные сети прямого распространения (многослойные персептроны) [10]. В качестве аппроксиматора функций могут использоваться также радиальные нейронные сети. При прочих равных условиях аппроксимация этими сетям требуется на порядки больше нейронов, чем аппроксимация многослойными персептронами. Поэтому радиальные нейронные сети в работе не рассматриваются.
Для решения прямой и обратной задачи построения области достижимости используем нейронные сети НС1, НС2 соответственно. Входами нейронной сети НС1 являются вектор начальных условий ![]() , конечный момент времени
, конечный момент времени ![]() и совокупность управлений
и совокупность управлений ![]() , а выходами - вектор
, а выходами - вектор ![]() - см. рисунок 2а. Нейронная сеть НС2 имеет в качестве входов величины
- см. рисунок 2а. Нейронная сеть НС2 имеет в качестве входов величины ![]() ,
, ![]() ,
, ![]() , а в качестве выходов - вектор
, а в качестве выходов - вектор ![]() - см. рисунок 2б.
- см. рисунок 2б.
В случае, когда известно множество допустимых управлений ![]() , приводящих систему (3) на границу области достижимости
, приводящих систему (3) на границу области достижимости ![]() , можно использовать сети, аналогичные сетям НС1, НС2. Отличие состоит в том, что здесь управления
, можно использовать сети, аналогичные сетям НС1, НС2. Отличие состоит в том, что здесь управления ![]() должны принадлежать множеству
должны принадлежать множеству ![]() , а вектор
, а вектор ![]() - границе
- границе ![]() . Кроме того, в случае сложной топологии границы
. Кроме того, в случае сложной топологии границы ![]() может оказаться необходимым использование различных нейронных сетей для аппроксимации различных фрагментов этой границы.
может оказаться необходимым использование различных нейронных сетей для аппроксимации различных фрагментов этой границы.

Рис. 2. К нейросетевой аппроксимации области достижимости
5. Пример
5.1. Постановка задачи.Рассмотрим летальный аппарат, уравнения движения центра масс которого в нормальной земной системе координат ![]() описываются системой нелинейных дифференциальных уравнений
описываются системой нелинейных дифференциальных уравнений
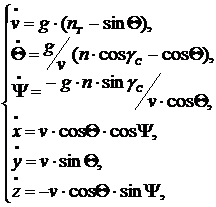 (14)
(14)
где ![]() – скорость летательного аппарата,
– скорость летательного аппарата, ![]() – угол наклона траектории,
– угол наклона траектории, ![]() – угол поворота траектории,
– угол поворота траектории, ![]() – высота летательного аппарата,
– высота летательного аппарата, ![]() – тангенциальная перегрузка,
– тангенциальная перегрузка, ![]() – нормальная перегрузка,
– нормальная перегрузка, ![]() – скоростной угол крена,
– скоростной угол крена, ![]() – ускорение свободного падения [1].
– ускорение свободного падения [1].
Управлениями летательного аппарата являются тангенциальная перегрузка, нормальная перегрузка и скоростной угол крена, так что ![]() . На управления наложены ограничения
. На управления наложены ограничения
![]()
![]()
![]()
![]()
![]()
![]()
В работе [1] показано, что дальняя, ближняя и боковая границы области достижимости системы (14) формируются управлениями, принадлежащими классу кусочно-постоянных управлений. Ограничимся рассмотрением дальней границы области достижимости. Для каждого допустимого ![]() структура управлений, формирующих эту границу, представлена на рисунках 3а, 3б [1].
структура управлений, формирующих эту границу, представлена на рисунках 3а, 3б [1].

Рис. 3. Структура управлений, формирующих дальнюю границу области достижимости
5.2. Метод мультифиниша.
Для экспериментального исследования эффективности метода мультифиниша разработана MPI-программа [4], реализующая этот метод. Эксперименты выполнены на виртуальном кластере, созданном с помощью программной системы VMware [11] и функционирующим под управлением свободно распространяемой операционной системы Ubuntu [12]. Результаты экспериментов иллюстрирует рисунок 4, который показывает, что на числе процессоров от 2 до 10 достигается ускорение, близкое к расчетному.

Рис. 4. Ускорение метода мультифиниша
Приведенные на рисунке 4 экспериментальные результаты получены при следующих значениях параметров задачи: ![]() м/с;
м/с; ![]() ;
; ![]() ;
; ![]() ;
; ![]() м;
м; ![]() ;
; ![]() с.
с.
5.3. Аппроксимация векторного поля системы ОДУ. Рассмотрим «плоскую» задачу (14), когда ![]() ,
, ![]() . Время
. Время ![]() положим равным 30 с. Область фазового пространства
положим равным 30 с. Область фазового пространства ![]() системы (14), положим, определяется неравенствами
системы (14), положим, определяется неравенствами
![]() ,
, ![]()
![]() ,
,
![]() м,
м, ![]() м,
м, ![]() .
.
Здесь ![]() м/с- скорость звука в воздухе. Начальные условия летального аппарата примем следующими:
м/с- скорость звука в воздухе. Начальные условия летального аппарата примем следующими: ![]() м/с;
м/с; ![]() ;
; ![]() ;
; ![]() ;
; ![]() м;
м; ![]() ;
; ![]() .
.
В соответствии с методикой, рассмотренной в разделе 3, покроем интервал времени ![]() равномерной сеткой с 20 узлами. Указанную выше область
равномерной сеткой с 20 узлами. Указанную выше область ![]() фазового пространства системы (14) покроем равномерной сеткой так, что количество шагов этой сетки равно 18, 20, 20, 18 по измерениям
фазового пространства системы (14) покроем равномерной сеткой так, что количество шагов этой сетки равно 18, 20, 20, 18 по измерениям ![]() ,
, ![]() ,
, ![]() ,
, ![]() соответственно. Наконец, в качестве моментов времени
соответственно. Наконец, в качестве моментов времени ![]() переключения управления
переключения управления ![]() рассмотрим
рассмотрим ![]() узлов равномерной сетки, покрывающей интервал времени
узлов равномерной сетки, покрывающей интервал времени ![]() (рисунок 3а).
(рисунок 3а).
Численные эксперименты выполнены для кусочно-постоянной аппроксимации функции ![]() на указанной сетке (рисунок 5).
на указанной сетке (рисунок 5).
Эксперименты показали, что метод обеспечивает погрешность в определении расстояния от начала координат до границы области достижимости, не превышающую 4%. В качестве точного положения границы области достижимости принималось положение, полученное путем численного интегрирования системы (14) при соответствующем управлении.

Рис. 5. Дальняя граница области достижимости («плоская» задача):
![]() - точная граница;
- точная граница; ![]() - приближенная граница
- приближенная граница
5.4. Нейросетевая аппроксимация. В данном случае начальный угол поворота траектории ![]() и начальные координаты
и начальные координаты ![]() ,
, ![]() ,
, ![]() летательного аппарата полагаются равными нулю. Так что исходное положение летательного аппарата определяется начальной скоростью
летательного аппарата полагаются равными нулю. Так что исходное положение летательного аппарата определяется начальной скоростью ![]() и начальным углом наклона траектории
и начальным углом наклона траектории ![]() :
: ![]() ;
; ![]() . Варьируемыми параметрами являются точки переключения
. Варьируемыми параметрами являются точки переключения ![]() нормальной перегрузки
нормальной перегрузки ![]() и значения скоростного угла крена
и значения скоростного угла крена ![]() . Полагается, что
. Полагается, что ![]() , где
, где ![]() с; поскольку область достижимости симметрична относительности плоскости
с; поскольку область достижимости симметрична относительности плоскости ![]() , полагается, что
, полагается, что ![]()
Для указанной задачи были построены нейронные сети НС1, НС2 (раздел 4). Во всех случаях обучающая выборка состояла из 4500 элементов, из которых 20% случайно выбранных точек использовались в качестве проверочных для определения момента окончания обучения. Начальные веса и пороговые значения нейронов слоя устанавливались в соответствии с алгоритмом инициализации Нгуен-Видроу (Nguyen-Widrow) [10]. Обучение каждой сети выполнялось в среднем 10 раз с различными начальными весами и пороговыми значениями, на основе чего выбиралась сеть с минимальным значением ошибки. Для исследования точности обученной сети использовалась тестовая выборка, содержащей более 20000 элементов. Все эксперименты выполнены в среде программной системы MatLab 6 [10].
Сеть НС1. Входной слой сети НС1 состоит из пяти элементов, соответствующих величинам ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Сеть содержит два скрытых слоя, содержащих одинаковое количество нейронов с функцией активации – гиперболический тангенс. Выходной слой сети состоит из трех нейронов с линейной функцией активации, соответствующих координатам
. Сеть содержит два скрытых слоя, содержащих одинаковое количество нейронов с функцией активации – гиперболический тангенс. Выходной слой сети состоит из трех нейронов с линейной функцией активации, соответствующих координатам ![]()
![]()
![]() конечного положения летательного аппарата.
конечного положения летательного аппарата.
Исследование показало, что при количестве нейронов в сети, равном 22, максимальная относительная ошибка определения нейронной сетью НС1 координат точек границы области достижимости не превышает 12%. С ростом количества нейронов эта ошибка быстро уменьшается и при 40 нейронах не превышает 4%. Результаты исследования иллюстрирует рисунок 6, на котором показана аппроксимация дальней границы области достижимости нейронной сетью НС1 с 32 нейронами для случая ![]() с,
с, ![]()
![]() .
.
Сеть НС2 аналогична сети НС1. Входной слой сети НС2 состоит из пяти элементов, соответствующих величинам ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , где
, где ![]() ,
, ![]() - углы, задающие требуемое направление в пространстве. Выходной слой состоит из двух нейронов, соответствующих положению точки переключения
- углы, задающие требуемое направление в пространстве. Выходной слой состоит из двух нейронов, соответствующих положению точки переключения ![]() и значения скоростного угла крена
и значения скоростного угла крена ![]() .
.

Рис. 6. Нейросетевая аппроксимация дальней границы области достижимости
Для оценки точности аппроксимации сети определяются координаты точек ![]() границы области достижимости, соответствующие управлению, получаемому на выходе нейронной сети, и сравниваются с эталонными координатами этих точек, вычисленными с помощью интегрирования системы ОДУ (14), как показано на рисунке 7.
границы области достижимости, соответствующие управлению, получаемому на выходе нейронной сети, и сравниваются с эталонными координатами этих точек, вычисленными с помощью интегрирования системы ОДУ (14), как показано на рисунке 7.
Исследование показало, что максимальная относительная ошибка определения нейронной сетью НС2 координат точек границы области достижимости при 22 нейронах в сети не превышает 9%, а при 40 нейронах - ~3%.
Детально результаты исследования метода нейросетевой аппроксимации границы области достижимости летального аппарата приведены в работах [13, 14].

Рис. 7. Схема определения точности аппроксимации нейронной сетью НС2
Заключение
В работе рассмотрены три метода построения области достижимости динамической системы – метод мультифиниша, метод на основе аппроксимации векторного поля соответствующей системы ОДУ, а также метод на основе нейронных сетей. Предложены соответствующие последовательные и параллельные алгоритмы, последние из которых ориентированы на вычислительные системы класса MIMD. Эффективность указанных методов исследована на примере построения области достижимости летательного аппарата (точнее, границы этой области).
Проведенное исследование показало перспективность практического использования всех рассмотренных методов. Тот или иной метод могут быть рекомендованы в зависимости от вычислительной сложности правых частей системы ОДУ, описывающей исследуемую динамическую систему, а также от располагаемых вычислительных ресурсов.
Кроме рассмотренных методов, интерес представляет использование для приближенного построения области достижимости нечетких множеств. Отметим также целесообразность исследования метода, основная идея которого состоит в следующем: для представительного множества начальных условий динамической системы тем или иным образом строим совокупность областей достижимости; границу каждой из этих областей аппроксимируем подходящей функцией; функциональную зависимость коэффициентов этой функции от начальных условий аппроксимируем, например, с помощью нейронной сети. Можно ожидать, что такой метод позволит получить приемлемую точность аппроксимации множества достижимости для широкого набора начальных условий.
Авторы благодарят Трофимова А.Г. за идею использования нейронных сетей для аппроксимации непосредственно области достижимости, а также К.О. Вишневецкого и Д.С. Кулеша за проведение вычислений с использованием методов мультифиниша и аппроксимации векторного поля соответственно.
Литература
1. Воронов, Е.М. Алгоритм оценки границ области достижимости летательного аппарата с учетом тяги / Е.М.Воронов, А.А.Карпунин // Вестник МГТУ. Сер. Приборостроение.- 2007.- ╧4(69).- С. 81-99.
2. Гурман, В.И. Приближенные методы оптимизации управления летальным аппаратом / В.И.Гурман, В.И.Квоков, М.Ю.Ухин // Автоматика и телемеханика.- 2008.- ╧4.-С. 191–201.
3. Ортега, Дж. Введение в численные методы решения дифференциальных уравнений / Дж.Ортега, У.Пул: пер.с англ.; под редакцией А.А.Абрамова - М.: Наука, 1986.- 288 с.
4. Воеводин, В.В. Параллельные вычисления / В.В.Воеводин.– СПб.: БХВ-Петербург, 2004.– 608 с.
5. Скворцов, А.В. Обзор алгоритмов построения триангуляции Делоне / А.В.Скворцов // Вычислительные методы и программирование.- 2002.-Т.3.-С. 14 – 39.
6. DirectoryofComputationalGeometrySoftware [Электронный ресурс]. (//http://www.geom.uiuc.edu/software/cglist/).
7. Карпенко, А.П. Аппроксимация функции предпочтений лица, принимающего решения, в задаче многокритериальной оптимизации. 1. Методы на основе планов первого порядка [Электронный ресурс] / А.П.Карпенко, В.Г.Федорук // Электронное научно-техническое издание: наука и образование.- 2008.- ╧3. (http://technomag.edu.ru/doc/82725.html).
8. Карпенко, А.П. Аппроксимация функции предпочтений лица, принимающего решения, в задаче многокритериальной оптимизации. 2. Методы на основе планов второго порядка [Электронный ресурс] / А.П.Карпенко, В.Г.Федорук // Электронное научно-техническое издание: наука и образование.- 2008.- ╧3. (http://technomag.edu.ru/doc/83356.html).
9. Хохлов, С.Ф. Применение метода Брандона для обработки экспериментальных данных / С.Ф.Хохлов, О.И.Школа // Вопросы химии и химической технологов.-1973.- Вып. 28.- с. 204—207.
10. Медведев, В.С. Нейронные сети. Matlab 6 // В.С.Медведев, В.Г.Потемкин.– М.: Диалог-МИФИ, 2001.– 496 с.
11. VM ware [Электронный ресурс]. (http://www.vmware.com/)
12. Ubuntu [Электронный ресурс]. (http://www.ubuntu.com/)
13. Козлова, О.Г. Нейросетевая аппроксимация границы области достижимости летательного аппарата [Электронный ресурс] / О.Г.Козлова // Электронное научно-техническое издание: наука и образование.- 2009.- ╧7. (http://technomag.edu.ru/doc/129990.html).
14. Козлова, О.Г. Нейросетевая аппроксимация границы области достижимости летательного аппарата. Трехмерный случай [Электронный ресурс] / О.Г.Козлова // Электронное научно-техническое издание: наука и образование.- 2009.- ╧8. (http://technomag.edu.ru/doc/130282.html).
Публикации с ключевыми словами: динамическая система, нейросетевая аппроксимация, область достижимости динамической системы
Публикации со словами: динамическая система, нейросетевая аппроксимация, область достижимости динамической системы
Смотри также:
- Нейросетевая аппроксимация границы области достижимости летательного аппарата. 2. Трехмерный случай
- Нейросетевая аппроксимация границы области достижимости летательного аппарата
- Нейросетевая аппроксимация векторного поля динамической системы в задаче приближенного построения области достижимости летательного аппарата
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



