научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 01, январь 2010
МГТУ им Н.Э.Баумана,
Chuchueva@yandex.ru
В июле 2009 года в издании «Наука и образование» была опубликована статья «Экстраполяция псевдослучайных процессов по максимуму подобия», в которой подробно рассматривалась основа модели. В настоящей статье продолжаем обзор и пояснения предлагаемого метода экстраполяции и более подробно представляем результаты экстраполяции.
Кратко напомним, что экстраполяция по максимуму подобия (далее ЭМП), выполняется на основании приведенных зависимостей.
Пусть есть исходная последовательность ![]() длины T. Для этой последовательности необходимо решить задачу экстраполяции в точках
длины T. Для этой последовательности необходимо решить задачу экстраполяции в точках ![]() на основании максимума подобия. Обращаем внимание, что верхним индексом определяется длина вектора, а нижним его начало на оси времени.
на основании максимума подобия. Обращаем внимание, что верхним индексом определяется длина вектора, а нижним его начало на оси времени.
В качестве меры подобия двух векторов внутри одной псевдослучайной последовательности используем линейную корреляцию Пирсона.
![]() (1)
(1)
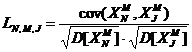 , (2)
, (2)
где ![]() — ковариация исходных векторов, а
— ковариация исходных векторов, а![]() и
и ![]() их дисперсии. Причем при N=J
их дисперсии. Причем при N=J ![]() .
.
Тогда функция подобия
![]() (3)
(3)
возвращает вектор значений модулей коэффициентов линейной корреляции со всеми векторами длины M, лежащими левее ![]() на оси времени. Результирующий вектор L(i) имеет длину N-1, назовём его вектором подобия.
на оси времени. Результирующий вектор L(i) имеет длину N-1, назовём его вектором подобия.
Тогда вектор ![]() , соответствующий максимальному значению L(i)
, соответствующий максимальному значению L(i)
![]() (4)
(4)
назовем максимумом подобия для исходного вектора![]() .
.
Далее введем предположение о том, что если ![]() и
и ![]() имеют высокое подобие, то есть модуль линейного коэффициента корреляции Пирсона близок к 1, то вектора
имеют высокое подобие, то есть модуль линейного коэффициента корреляции Пирсона близок к 1, то вектора ![]() и
и ![]() будут также иметь высокое подобие. Данное рассуждение назовем предположением о подобии. На основании предположения о подобии решается задача экстраполяции вектора
будут также иметь высокое подобие. Данное рассуждение назовем предположением о подобии. На основании предположения о подобии решается задача экстраполяции вектора ![]() в точках
в точках ![]() .
.
В связи с тем, что в качестве меры подобия был использован коэффициент линейной корреляции, то экстраполированные значения будут определяться линейной зависимостью:
![]() (5)
(5)
Согласно предположению о подобии в качестве ![]() берем вектор
берем вектор ![]() , то есть вектор, лежащий на оси времени сразу за вектором максимума подобия. Решение задачи нахождения матрицы A подробно описано в указанной статье «Экстраполяция псевдослучайных процессов по максимуму подобия». Положения упомянутых векторов наглядно представлены на рис 1.
, то есть вектор, лежащий на оси времени сразу за вектором максимума подобия. Решение задачи нахождения матрицы A подробно описано в указанной статье «Экстраполяция псевдослучайных процессов по максимуму подобия». Положения упомянутых векторов наглядно представлены на рис 1.

Рис 1. Положения векторов ![]() ,
,![]() ,
,![]() и
и![]() на оси времени
на оси времени
Таким образом, экстраполированные значения исходной последовательности определяются согласно (6):
![]() (6)
(6)
Если переписать равенство (6) формально, то получаем определение модели ЭМП (MLE = maximum likeness extrapolation).
![]() (7)
(7)
Введенная модель ЭПМ имеет один параметр – длина векторов M. Влияние этого параметра на точность экстраполяции будет продемонстрировано ниже.
Для оценки работы модели были взяты 2 ряда потребления и 2 ряда цен на ОРЭМ:
1) Потребление ценовой зоны Европы (ТГ по первой ценовой зоне)
2) Цена РСВ (рынок на сутки вперед) ценовой зоны Европы
3) Потребление ценовой зоны Сибири (ТГ по второй ценовой зоне)
4) Цена РСВ (рынок на сутки вперед) ценовой зоны Сибири
Каждый ряд содержит почасовые значения в диапазоне: 01.09.2006 до 30.09.2009 (около 27000 значений). Результаты оценивались при помощи двух видов ошибок MAE и MAPE. MAE (mean absolute error) – средняя абсолютная ошибка, определяемая по формуле:
![]() (8)
(8)
MAPE (mean absolute percentage error) – средняя абсолютная ошибка в процентах, определяемая по формуле:
![]() (9)
(9)
Схема расчетов представлена ниже.

Рис 2. Алгоритм идентификации модели и последующей экстраполяции
Каждый рассмотренный временной ряд был разделен на три непересекающихся отрезка: базовый, исследовательский и контрольный. Кроме того, для каждого временного ряда проводилась экстраполяция агрегированных данных для дополнительной проверки работоспособности алгоритма. Вся агрегация проводилась внутри суток, путем суммирования (для потребления) или осреднения (для цен) значений в зависимости от степени агрегации (см. таблицу 1).
Таблица 1. Виды агрегации
|
Тип ряда
|
Тип агрегации
|
Исходное кол-во значений внутри суток
|
Результирующее кол-во значений внутри суток
|
Кол-во экстраполируемых значений (параметр P)
|
Обозначение M* на рис 1.
|
|
Потребление
|
Без агрегации
|
24
|
24
|
24
|
M1*
|
|
Сумма 2-х часов
|
24
|
12
|
12
|
M2*
|
|
|
Сумма 3-х часов
|
24
|
8
|
8
|
M3*
|
|
|
Сумма 4-х часов
|
24
|
6
|
6
|
M4*
|
|
|
Сумма 6-и часов
|
24
|
4
|
4
|
M6*
|
|
|
Сумма 12-и часов
|
24
|
2
|
2
|
M12*
|
|
|
Сумма 24-х часов
|
24
|
1
|
1
|
M24*
|
|
|
Цена
|
Без агрегации
|
24
|
24
|
24
|
M1*
|
|
Среднее 2-х часов
|
24
|
12
|
12
|
M2*
|
|
|
Среднее 3-х часов
|
24
|
8
|
8
|
M3*
|
|
|
Среднее 4-х часов
|
24
|
6
|
6
|
M4*
|
|
|
Среднее 6-и часов
|
24
|
4
|
4
|
M6*
|
|
|
Среднее 12-и часов
|
24
|
2
|
2
|
M12*
|
|
|
Среднее 24-х часов
|
24
|
1
|
1
|
M24*
|
Далее, проводилась экстраполяция исследовательского отрезка при различных значениях параметрах M; базовый отрезок выступал в качестве исторических данных. В результате экстраполяции мы получали зависимость абсолютной ошибки MAE от параметра M. Пример такой зависимости представлен на рис 3.

Рис 3. Зависимость точности экстраполяции исследовательского отрезка от параметра M
По результатам экстраполяции мы получали значение M*, соответствующее минимуму ошибки для каждого исследуемого ряда и всех его агрегаций.
В связи с тем, что алгоритм способен работать как со стационарными рядами, так и с нестационарными, то дополнительно каждый из рядов (изначально не стационарный) приводился к стационарности первого порядка двумя алгоритмами (10), (11).
![]() (10)
(10)
![]() (11)
(11)
В первом случае бралась разность соседних значений; во втором значение N зависело от степени агрегации ряда: для разрешения 24 значения в сутки N = 24, для разрешения 12 значений в сутки N = 12 и т.д. Таким образом, во втором варианте ряд приводился к стационарности путем получения разности значений в соответствующие часы соседних суток. Обращаем внимание на то, что при агрегации данных до единого значения в сутки формулы (10) и (11) становятся идентичными.
В завершении проводилась экстраполяции контрольного отрезка на основании значений M*, полученных в результате исследований. Результаты экстраполяций представлены в таблицах ниже.
1) Потребление ценовой зоны Европы (ТГ по первой ценовой зоне)
Таблица 2. Результаты экстраполяции
|
Тип стационарности
|
Тип агрегации
|
M*
|
MAE, МВт.ч
|
MAPE,
%
|
Время исследований, час
|
Время экстраполяции, час
|
|
Исходные данные (нестационарные)
|
Без агрегации
|
216
|
1347
|
1.8035
|
18.4
|
1.80
|
|
Сумма 2-х часов
|
60
|
2008
|
1.3443
|
14.2
|
1.10
|
|
|
Сумма 3-х часов
|
40
|
3079
|
1.3689
|
9.9
|
0.61
|
|
|
Сумма 4-х часов
|
30
|
4192
|
1.4039
|
9.2
|
0.43
|
|
|
Сумма 6-и часов
|
17
|
5433
|
1.2116
|
4.7
|
0.25
|
|
|
Сумма 12-и часов
|
12
|
10270
|
1.1442
|
4.2
|
0.11
|
|
|
Сумма 24-х часов
|
6
|
19736
|
1.0984
|
2.8
|
0.15
|
|
|
Стационарность
по типу 1
|
Без агрегации
|
216
|
916
|
1.2204
|
-
|
3.40
|
|
Сумма 2-х часов
|
60
|
1944
|
1.2746
|
-
|
1.12
|
|
|
Сумма 3-х часов
|
40
|
3044
|
1.3194
|
-
|
0.67
|
|
|
Сумма 4-х часов
|
30
|
3792
|
1.2463
|
-
|
0.42
|
|
|
Сумма 6-и часов
|
17
|
5741
|
1.2620
|
-
|
0.26
|
|
|
Сумма 12-и часов
|
12
|
9803
|
1.0917
|
-
|
0.14
|
|
|
Сумма 24-х часов
|
6
|
27267
|
1.4905
|
-
|
0.05
|
|
|
Стационарность по типу 2
|
Без агрегации
|
216
|
781
|
1.0378
|
-
|
3.55
|
|
Сумма 2-х часов
|
60
|
1755
|
1.1654
|
-
|
1.16
|
|
|
Сумма 3-х часов
|
40
|
2559
|
1.1345
|
-
|
0.56
|
|
|
Сумма 4-х часов
|
30
|
3368
|
1.1193
|
-
|
0.35
|
|
|
Сумма 6-и часов
|
17
|
6279
|
1.3544
|
-
|
0.20
|
|
|
Сумма 12-и часов
|
12
|
12569
|
1.3600
|
-
|
0.10
|
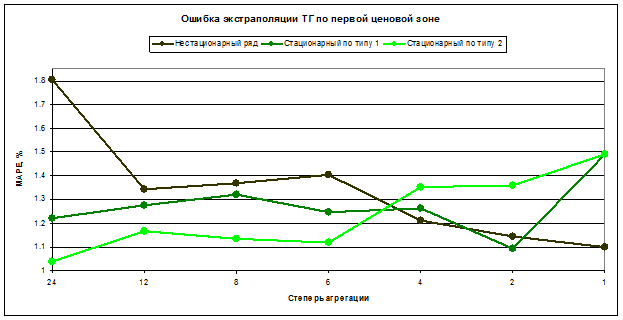
Рис 4. График зависимости точности экстраполяции от типа стационарности и вида агрегации
На приведенном выше графике заметно, что по мере большей интеграции данных по потреблению точность экстраполяции увеличивается, что закономерно. Кроме того, стоит отметить, что при приведении ряда к стационарности первого порядка на основании (11) точность экстраполяции существенно возрастает при низкой степени агрегации данных.
2) Цена РСВ ценовой зоны Европы (Црсв по первой ценовой зоне)
Таблица 3. Результаты экстраполяции
|
Тип стационарности
|
Тип агрегации
|
M*
|
MAE, Руб/МВт.ч
|
MAPE,
%
|
Время исследований, час
|
Время экстраполяции, час
|
|
Исходные данные (нестационарные)
|
Без агрегации
|
360
|
49.54
|
9.1561
|
42.90
|
2.10
|
|
Среднее 2-х часов
|
78
|
42.67
|
7.9390
|
32.86
|
1.06
|
|
|
Среднее 3-х часов
|
52
|
41.54
|
7.3055
|
21.78
|
0.54
|
|
|
Среднее 4-х часов
|
39
|
40.25
|
6.9081
|
16.16
|
0.34
|
|
|
Среднее 6-и часов
|
28
|
38.37
|
6.5862
|
10.92
|
0.20
|
|
|
Среднее 12-и часов
|
30
|
38.50
|
6.3386
|
5.39
|
0.10
|
|
|
Среднее 24-х часов
|
16
|
34.50
|
5.5754
|
2.79
|
0.04
|
|
|
Стационарность
по типу 1
|
Без агрегации
|
360
|
47.08
|
8.5243
|
-
|
4.70
|
|
Среднее 2-х часов
|
78
|
48.23
|
8.5991
|
-
|
1.28
|
|
|
Среднее 3-х часов
|
52
|
44.38
|
7.8799
|
-
|
0.60
|
|
|
Среднее 4-х часов
|
39
|
43.44
|
7.4189
|
-
|
0.37
|
|
|
Среднее 6-и часов
|
28
|
39.98
|
6.8292
|
-
|
0.20
|
|
|
Среднее 12-и часов
|
30
|
34.10
|
5.6411
|
-
|
0.10
|
|
|
Среднее 24-х часов
|
16
|
29.85
|
4.8102
|
-
|
0.05
|
|
|
Стационарность по типу 2
|
Без агрегации
|
360
|
38.76
|
7.0019
|
-
|
4.71
|
|
Среднее 2-х часов
|
78
|
39.90
|
7.0900
|
-
|
1.28
|
|
|
Среднее 3-х часов
|
52
|
39.56
|
6.7733
|
-
|
0.61
|
|
|
Среднее 4-х часов
|
39
|
40.01
|
6.6974
|
-
|
0.36
|
|
|
Среднее 6-и часов
|
28
|
38.12
|
6.4190
|
-
|
0.20
|
|
|
Среднее 12-и часов
|
30
|
32.33
|
5.3125
|
-
|
0.10
|

Рис 5. График зависимости точности экстраполяции от типа стационарности и вида агрегации
3) Потребление ценовой зоны Сибири (ТГ по второй ценовой зоне)
Таблица 4. Результаты экстраполяции
|
Тип стационарности
|
Тип агрегации
|
M*
|
MAE, МВт.ч
|
MAPE,
%
|
Время исследований, час
|
Время экстраполяции, час
|
|
Исходные данные (нестационарные)
|
Без агрегации
|
24
|
378
|
1.8640
|
13.29
|
4.20
|
|
Сумма 2-х часов
|
30
|
583
|
1.4401
|
11.84
|
1.19
|
|
|
Сумма 3-х часов
|
24
|
875
|
1.4428
|
7.63
|
0.57
|
|
|
Сумма 4-х часов
|
18
|
1129
|
1.3924
|
6.30
|
0.38
|
|
|
Сумма 6-и часов
|
30
|
1632
|
1.3354
|
3.91
|
0.20
|
|
|
Сумма 12-и часов
|
13
|
3213
|
1.3212
|
1.88
|
0.10
|
|
|
Сумма 24-х часов
|
8
|
7727
|
1.5797
|
0.79
|
0.05
|
|
|
Стационарность
по типу 1
|
Без агрегации
|
24
|
385
|
1.8981
|
-
|
3.64
|
|
Сумма 2-х часов
|
30
|
597
|
1.4610
|
-
|
1.44
|
|
|
Сумма 3-х часов
|
24
|
892
|
1.4648
|
-
|
0.72
|
|
|
Сумма 4-х часов
|
18
|
1207
|
1.4912
|
-
|
0.40
|
|
|
Сумма 6-и часов
|
30
|
1444
|
1.1845
|
-
|
0.22
|
|
|
Сумма 12-и часов
|
13
|
3115
|
1.2831
|
-
|
0.10
|
|
|
Сумма 24-х часов
|
8
|
7098
|
1.4389
|
-
|
0.05
|
|
|
Стационарность по типу 2
|
Без агрегации
|
24
|
439
|
2.1590
|
-
|
3.74
|
|
Сумма 2-х часов
|
30
|
708
|
1.7398
|
-
|
1.12
|
|
|
Сумма 3-х часов
|
24
|
1153
|
1.8914
|
-
|
0.62
|
|
|
Сумма 4-х часов
|
18
|
1475
|
1.8133
|
-
|
0.39
|
|
|
Сумма 6-и часов
|
30
|
1639
|
1.3426
|
-
|
0.21
|
|
|
Сумма 12-и часов
|
13
|
3507
|
1.4416
|
-
|
0.05
|
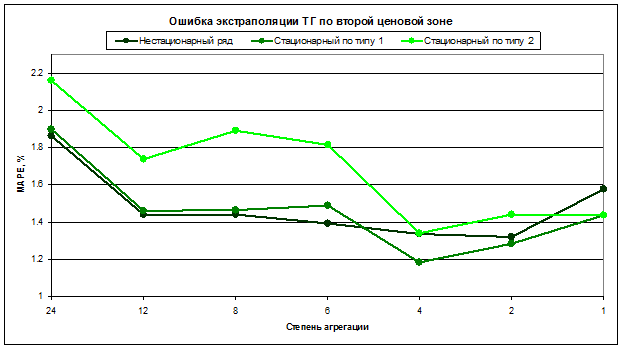
Рис 6. График зависимости точности экстраполяции от типа стационарности и вида агрегации
4) Цена РСВ ценовой зоны Сибири (Црсв по второй ценовой зоне)
Таблица 5. Результаты экстраполяции
|
Тип стационарности
|
Тип агрегации
|
M*
|
MAE, Руб/МВт.ч
|
MAPE[1],
%
|
Время исследований, час
|
Время экстраполяции, час
|
|
Исходные данные (нестационарные)
|
Без агрегации
|
84
|
65.90
|
43.7431
|
20.20
|
4.93
|
|
Среднее 2-х часов
|
60
|
68.17
|
43.6596
|
14.15
|
1.25
|
|
|
Среднее 3-х часов
|
28
|
68.70
|
43.2658
|
8.71
|
0.63
|
|
|
Среднее 4-х часов
|
72
|
64.19
|
44.1970
|
7.28
|
0.41
|
|
|
Среднее 6-и часов
|
40
|
64.09
|
41.4060
|
3.99
|
0.22
|
|
|
Среднее 12-и часов
|
25
|
62.99
|
38.9923
|
2.20
|
0.10
|
|
|
Среднее 24-х часов
|
30
|
60.39
|
38.6383
|
0.82
|
0.04
|
|
|
Стационарность
по типу 1
|
Без агрегации
|
84
|
64.91
|
39.7805
|
-
|
5.09
|
|
Среднее 2-х часов
|
60
|
67.05
|
42.2671
|
-
|
1.34
|
|
|
Среднее 3-х часов
|
28
|
67.39
|
42.1989
|
-
|
0.65
|
|
|
Среднее 4-х часов
|
72
|
70.04
|
37.4172
|
-
|
0.40
|
|
|
Среднее 6-и часов
|
40
|
67.82
|
36.8110
|
-
|
0.21
|
|
|
Среднее 12-и часов
|
25
|
62.50
|
33.1753
|
-
|
0.10
|
|
|
Среднее 24-х часов
|
30
|
62.52
|
32.9309
|
-
|
0.04
|
|
|
Стационарность по типу 2
|
Без агрегации
|
84
|
84.57
|
44.7243
|
-
|
5.09
|
|
Среднее 2-х часов
|
60
|
80.42
|
42.8597
|
-
|
1.32
|
|
|
Среднее 3-х часов
|
28
|
82.23
|
43.0731
|
-
|
0.63
|
|
|
Среднее 4-х часов
|
72
|
67.02
|
38.2477
|
-
|
0.37
|
|
|
Среднее 6-и часов
|
40
|
69.99
|
36.3611
|
-
|
0.20
|
|
|
Среднее 12-и часов
|
25
|
67.36
|
33.9110
|
-
|
0.01
|
Рис 7. График зависимости точности экстраполяции от типа стационарности и вида агрегации
В завершении данной статьи обращаем внимание читателей на два момента.
В-первых, отметим, что все представленные расчеты проводились на одном расчетном ядре, особенности каждого отдельного ряда не учитывались при экстраполяции. Существует несколько способов повышения точностей, которых уже удалось добиться при помощи реализации базового алгоритма. Указанные ниже способы детально не рассматриваются в представленной статье, однако их применение является дальнейшим развитием и адаптацией модели для конкретных задач и предметных областей:
1. Определять M* не для ряда целиком, а на каждый месяц, день недели, час дня в зависимости от тех результатов, которые мы получаем в процессе исследовательских расчетов.
2. Применение фильтрации, например, популярного скользящего среднего (moving average), которое сглаживает пиковые значения цен.
3. Участие в расчете не только временного ряда, который необходимо экстраполировать, но и внешних переменных, учет которых возможен благодаря регрессионной основе рассматриваемой модели.
Во-вторых, отмечаем, что представленные результаты экстраполяции показывают состоятельность предлагаемого метода прогнозирования для кривых ОРЭМ. В дальнейших публикациях планируется продемонстрировать результаты экстраполяции кривых из другой предметной области для выполнения оценки того, насколько базовый алгоритм готов работать с временными рядами, имеющими иной характер.
Литература
1. Э.Е. Тихонов, «Прогнозирование в условиях рынка», Невинномысск, 2006 г.
2. В. И. Суслов, Н. М. Ибрагимов, Л. П. Талышева, А. А. Цыплаков, «Эконометрия», И: Новосибирский государственный университет, 2005 г.
3. А.А. Грешилов, В.А. Стакун, А.А. Стакун, «Математические методы построения прогнозов», И: Москва, Радио и связь, 1997 г.
4. Дж. Бокс, Г. Дженкинс, «Анализ временных рядов», 1967 г.
5. Prajakta S. Kalekar, «Time series Forecasting using Holt-Winters and Exponential Smoothing», Kanwal Rekhi School of Information Technology, 2004
6. Uwe Hassler and JÄurgen Wolters, «Autoregressive Distributed Lag Models and Cointegration», 2005
7. Reinaldo C. Garcia, «A GARCH Forecasting Model to Predict Day-Ahead Electricity Prices», German Institute of Economic Research, DIW (Berlin), Germany, 2003
8. M. Sc. Jingfei Yang, «Power System Short-term Load Forecasting», Elektrotechnik und Informationstechnik der Technischen Universität Darmstadt, 2006
9. Herve Abdi, Multiple Correlation Coefficient, The University of Texas at Dallas, 2007
[1] При расчете MAPE нулевые значения Црсв заменялись на 0.01 Руб/МВт.ч во избежание возникновения деления на ноль.
Публикации с ключевыми словами: прогнозирование, Экстраполяция, временные ряды
Публикации со словами: прогнозирование, Экстраполяция, временные ряды
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



