научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 01, январь 2010
УДК: 62-408
kolobov@laspace.ru,
МГТУ им. Н.Э.Баумана
Задача оптимизации пространственной ориентации заготовки часто возникает при обработке заготовок с большими отклонениями формы для минимизации величины отходов при обработке заготовки, например, при черновой обработке.
Особую важность эта задача приобретает при центрировании чурака в фанерном производстве. От точности центрирования чурака зависит качество и объём получаемого шпона.
Задача центрирования чурака или определения его экономической оси сводится к задаче нахождения вписанного цилиндра (определения максимального диаметра идеального цилиндра и положения его оси в пространстве).
Для практического решения этой задачи необходим аналитический анализ отклонений формы и расположения чурака. При этом возникает необходимость в дифференциации комплексных показателей отклонений формы.
По отношению к цилиндрической поверхности различать совокупность отклонений всей поверхности, т.е. отклонение от цилиндричности и совокупность отклонений в сечениях, например, в поперечном – отклонения от круглости, в продольном – наклон или непрямолинейность образующей.
Введя цилиндрические координаты, можно уравнение реальной поверхности чурака представить в виде
![]() или
или ![]() ,
,
где r - радиус-вектор; j - угловая координата; z – осевая координата.
Уравнения профиля можно получить в виде сечений реальной цилиндрической поверхности плоскостями j0=const или z0=const. Тогда уравнения профилей будут иметь вид
![]() или
или ![]()
Если для поверхности идеального цилиндра ввести обозначения r0 – радиус цилиндра и l – длина цилиндра, то отклонение от цилиндричности можно представить в виде
![]() ,
,
где f – функция, описывающая поверхность чурака.
Соответственно, для отклонений от круглости получим
![]() или
или ![]() ,
,
а для отклонения от прямолинейности образующей
![]() или
или ![]() .
.
Разлагая функцию погрешностей в ряд Фурье, получим
![]() ,
,
где ak, bk – коэффициенты ряда Фурье; k – номер гармоники.
Введя обозначения ![]() и
и ![]() функцию погрешностей можно представить в виде
функцию погрешностей можно представить в виде
![]()
где k – номер гармоники; j - угловая координата; jk – фазовый угол для k-ой гармоники (фаза); сk – амплитуда k-ой гармоники.
Коэффициенты ряда Фурье в общем случае определяются по формулам
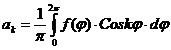

В реальных задачах при аппроксимации периодических функций вместо бесконечных рядов используются ряды с конечным количеством членов:
![]() .
.
С ростом количества членов ряда погрешность уменьшается.
Нулевой член ряда Фурье с0/2 является средним значением функции f(j) за период или постоянной составляющей отклонений текущего размера чурака.
Первый член ряда ![]() соответствует эксцентриситету.
соответствует эксцентриситету.
Второй член ряда Фурье ![]() характеризует овальность.
характеризует овальность.
Так как за величину овальности принимается разность между наибольшим и наименьшим диаметрами, то овальность равна учетверенной величине второго члена ряда - ![]() .
.
Так как эксцентриситет характеризуется амплитудой и фазой, его можно представить в виде вектора. Источниками возникновения эксцентриситета могут быть причины различного характера. В случае центрирования чурака это могут быть, например:
погрешности, вызванные схемой центрирования (например, центрирование на неподвижных призмах при наличии разброса диаметров чураков);
погрешности, вызванные неточностью изготовления центрирующего устройства (например, эксцентриситет, возникающий из-за неравенства углов опорных призм, т.е. погрешности изготовления центрирующего устройства);
погрешности из-за эксцентриситета центрирующего устройства и центров лущильного станка (сюда можно отнести и погрешности сборки);
погрешности формы чурака (например, овальность) и др.
Эксцентриситеты, возникающие от разных причин, можно определять по раздельности. Результирующий эксцентриситет определяется путем суммирования по правилам сложения векторов с учетом их фаз.
Например при сложении двух эксцентриситетов, возникающих по разным причинам, выражение для результирующего эксцентриситета имеет вид
![]() ,
,
а для фазового угла

На практике аппроксимация профиля поперечного сечения объекта, имеющего отклонения от круглости, тригонометрическим полиномом осуществляется методами численного гармонического анализа.
Для аппроксимации функции f(j) на интервале (0, 2p) тригонометрическим полиномом
![]()
так, чтобы минимизировать сумму квадратов отклонений ![]() необходимо знать m значений функции f(jk)=yk при jk=2p/m. При этом должно быть
необходимо знать m значений функции f(jk)=yk при jk=2p/m. При этом должно быть ![]() .
.
Коэффициенты ak и bk определяются по формулам
![]()
![]() .
.
Формулы значительно упрощаются, если ограничится определением только первых трех гармоник. Этого вполне достаточно для нахождения экономического центра сечения чурака.
В этом случае необходимо знать значения функции поверхности в 12 точках с интервалом (p/12) и в четырех дополнительных точках (p/4), (3p/4), (5p/4), (7p/4):
6а0 = у0 + у1 + у2 + … + у11;
6а3 = у0 – у2 + у4 – у6 + у8 – у10;
4а2 = у0 – у3 + у6 – у9;
6b3 = у1 – у3 + у5 – у7 + у9 – у11;
a1 = ½( у0 – у6) + a3;
b1 = ½( у3 – у9) + b3;
4b2 = y(p/4) - y(3p/4) + y(5p/4) - y(7p/4).
В качестве примера рассмотрим гармонический анализ чурака, имеющего профиль поперечного сечения в виде смещенного и повернутого эллипса, представленного на .рисунке 1. Размер большой оси эллипса 2а = 98,5 мм, малой – 2b = 73 мм. Эллипс повернут на 30° и смещен на 12 мм.
|
|
|
Рис.1. Координаты поперечного сечения чурака
|
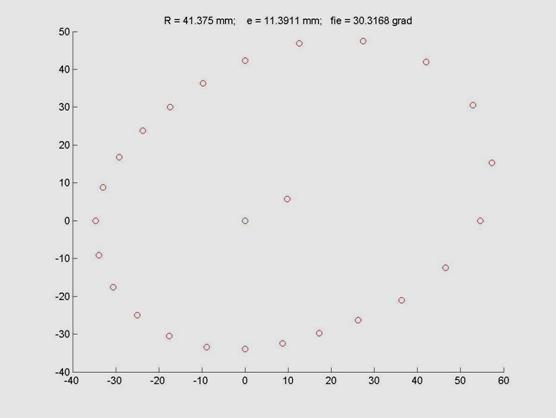
Поверхность чурака, аппроксимированная по результатам гармонического анализа с определением трех первых членов ряда, показана на рисунке 2. Синей точкой показан центр координат, красной – положение центра сечения по результатам гармонического анализа.
В результате получено значение эксцентриситета е = 11,3911 мм. Фазовый угол эксцентриситета - jе = 30,3168°.
Расхождение с исходными данными вызвано вычислительными погрешностями и погрешностями метода..
|
|
|
Рис.2 Аппроксимированное сечение чурака
|
Назовем линию, проходящую через координаты центра поперечного сечения чурака, определенные методами гармонического анализа, осью чурака.
При сканировании поверхности чурака в N сечениях по длине с последующим гармоническим анализом поперечных сечений чурака получаем массив из N эксцентриситетов поперечных сечений и массив фазовых углов эксцентриситетов. Эти два массива описывают положение в пространстве оси чурака.
При простой кривизне эта кривая представляет собой кривую второго порядка, расположенную в плоскости, проходящей через ось центров устройства проворота чурака при сканировании. При сложной кривизне чурака кривая будет описываться многочленом более высокого порядка.
Предлагается оптимизацию положения чурака в пространстве свести к двум независимым процедурам:
ü аппроксимации оси чурака, полученной в результате сканирования, прямой линией;
ü совмещении аппроксимирующей прямой с осью центров лущильного станка.
Наиболее распространенным способом сглаживания (аппроксимации) экспериментальных данных является метод наименьших квадратов, разработанный Гауссом.
Если при известном массиве пар экспериментальных данных ![]() ищется аппроксимирующая функция
ищется аппроксимирующая функция ![]() , то критерием выравнивания будет выражение
, то критерием выравнивания будет выражение
![]() .
.
При выравнивании прямыми ![]() необходимым и достаточным условием того, чтобы точки массива экспериментальных данных
необходимым и достаточным условием того, чтобы точки массива экспериментальных данных ![]() лежали на прямой, является пропорциональность разностей
лежали на прямой, является пропорциональность разностей ![]() и
и ![]() (i = 2, 3,…n), т.е.
(i = 2, 3,…n), т.е. ![]() .
.
При использовании для выражений суммирования обозначения ![]() выражения для определения коэффициентов a и b прямой имеют вид
выражения для определения коэффициентов a и b прямой имеют вид
![]()

При решении пространственной задачи аппроксимацию можно, без снижения точности аппроксимации, проводить раздельно в двух плоскостях XZ и YZ (ось Z – продольная ось чурака).
Блок-схема алгоритма оптимизации представлена на рисунке 3.
|
|
|
Рис.3 Блок-схема алгоритма оптимизации положения чурака в пространстве
|
В качестве примера рассмотрим оптимизацию положения в пространстве чурака 2 сорта, имеющего сложную кривизну с максимальной стрелой прогиба 48мм и конусность ![]() . Массив эксцентриситетов, полученных в результате сканирования в 7 сечениях и последующего гармонического анализа, - e=[0, 26.0, 45.5, 54.0, 49.5, 34.0, 12.0], массив фазовых углов - fi=[0, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0].
. Массив эксцентриситетов, полученных в результате сканирования в 7 сечениях и последующего гармонического анализа, - e=[0, 26.0, 45.5, 54.0, 49.5, 34.0, 12.0], массив фазовых углов - fi=[0, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0].
Результатом оптимизации явились следующие координаты оптимальных положений центров проворотного устройства (т.е. координаты центров после коррекции): одного торца - (22.0177, 13.4185, 0.0) и другого - (24.8058, 28.0880, 1600.0).
Исходная ось чурака и аппроксимирующая прямая представлены на рисунке 4.
|
|
|
Рис.4. Пример оптимизации положения чурака в пространстве
|
Литература:
1. Справочник по математике для инженеров и учащихся втузов. Бронштейн И.Н., Семендяев К.А. –М.: Наука. 1981.
2. ГОСТ 9462-88 Лесоматериалы круглые лиственных пород. Технические условия.
Публикации с ключевыми словами: точность, оптимизация
Публикации со словами: точность, оптимизация
Смотри также:
- Методика повышения точности системы позиционирования металлорежущих станков
- Возможности применения параллельных методов вычисления в системе программирования на языке S-FLOGOL
- Разработка программной среды для моделирования и оптимизации складской политики двухэшелонных многопродуктовых цепей поставки
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||