научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 01, январь 2010
Московский государственный текстильный университет
имени А.Н. Косыгина
В наследственной теории для описания нелинейной вязкоупругости металлов [1] и текстильных материалов [2-4,5] применяются ядра ползучести типа![]() и
и ![]() . Что касается ядер ползучести типа
. Что касается ядер ползучести типа ![]() , то возможность их применения в интегральных уравнениях для описания вязкоупругих свойств пряжи не была рассмотрена. Однако необходимо отметить, что при выборе ядер типа
, то возможность их применения в интегральных уравнениях для описания вязкоупругих свойств пряжи не была рассмотрена. Однако необходимо отметить, что при выборе ядер типа ![]() или
или ![]() для описания нелинейной вязкоупругости пряжи возникает вопрос, связанный с учетом активирующего действия напряжения на процесс деформации пряжи. Для его решения, при аналитическом описании вязкоупругих свойств полимерных материалов c использованием наследственной теории, активирующее влияние напряжения на процесс деформирования нитей и пряжи учитывается введением зависимости времени запаздывания
для описания нелинейной вязкоупругости пряжи возникает вопрос, связанный с учетом активирующего действия напряжения на процесс деформации пряжи. Для его решения, при аналитическом описании вязкоупругих свойств полимерных материалов c использованием наследственной теории, активирующее влияние напряжения на процесс деформирования нитей и пряжи учитывается введением зависимости времени запаздывания ![]() от напряжения
от напряжения ![]() :
:![]() , где
, где ![]() ,
, ![]() - энергия активации, определяемая из экспериментов на ползучесть исследуемого объекта при одноступенчатом нагружении,
- энергия активации, определяемая из экспериментов на ползучесть исследуемого объекта при одноступенчатом нагружении, ![]() – энергетическая константа. В частности, при неизменном механизме деформации в области малых напряжений зависимость энергии активации от напряжения имеет вид
– энергетическая константа. В частности, при неизменном механизме деформации в области малых напряжений зависимость энергии активации от напряжения имеет вид ![]() , где
, где ![]() - активационный объем [6,7]. При таком представлении о влиянии нагрузки на процесс деформации пряжи возникает вопрос, связанный с зависимостью изменения энергии активации от режимов деформирования. Очевидно, что одно и то же напряжение
- активационный объем [6,7]. При таком представлении о влиянии нагрузки на процесс деформации пряжи возникает вопрос, связанный с зависимостью изменения энергии активации от режимов деформирования. Очевидно, что одно и то же напряжение ![]() в образце можно получить при различных режимах нагружения, например: при нагружении образца в режиме ползучести, при нагружении в режиме релаксации напряжения, при нагружении в режиме с постоянной скоростью деформации. Также возникает вопрос, что является постоянной при достижении напряжения
в образце можно получить при различных режимах нагружения, например: при нагружении образца в режиме ползучести, при нагружении в режиме релаксации напряжения, при нагружении в режиме с постоянной скоростью деформации. Также возникает вопрос, что является постоянной при достижении напряжения ![]() при неизменном механизме деформации и при различных одностадийных режимах нагружения образца, энергия активации
при неизменном механизме деформации и при различных одностадийных режимах нагружения образца, энергия активации ![]() или
или ![]() и
и ![]() . Ответы на этот вопросы находятся в поле теоретических представлений о механизме деформации исследуемого объекта. К тому же, величину энергии активации исследуемого объекта можно определить только при проведении экспериментов на ползучесть при одноступенчатом нагружении.
. Ответы на этот вопросы находятся в поле теоретических представлений о механизме деформации исследуемого объекта. К тому же, величину энергии активации исследуемого объекта можно определить только при проведении экспериментов на ползучесть при одноступенчатом нагружении.
Приведенный материал, связанный с выбором ядер и с энергией активации, определяет разветвление в развитии аналитического описания пряжи с применением наследственной теории, и, соответственно, различие в решениях применяемых интегральных уравнений для описания нелинейной вязкоупругости исследуемого объекта, так как ядра ползучести интегральных уравнений являются функциями не только от времени, но и от энергии активации, и, следовательно, от времени запаздывания. Поэтому, целью данной работы является проведение исследований, связанных с возможностью применения интегральных уравнений с ядром ползучести ![]() , которое в преобразованной временной шкале представляется видом
, которое в преобразованной временной шкале представляется видом ![]() для описания и прогнозирования нелинейной вязкоупругости пряжи, с положением о независимости энергии активации от режимов деформации пряжи при её одностадийном нагружении до наперед заданного напряжения.
для описания и прогнозирования нелинейной вязкоупругости пряжи, с положением о независимости энергии активации от режимов деформации пряжи при её одностадийном нагружении до наперед заданного напряжения.
В качестве объекта исследования использовалась многокомпонентная пряжа (хлопок-30%, лен-20%, лавсан-50%). Линейная плотность пряжи -29 текс. Испытания на ползучесть проводили на релаксометре деформации конструкции каф. сопротивления материалов Санкт-Петербургского Государственного Университета Технологии и Дизайна. Испытания на растяжение с постоянной скоростью проводили на разрывной многофункциональной машине модели Инстрон – 1122. Испытания проводились при температуре ![]() . База – 100мм.
. База – 100мм.
Опираясь на основные положения наследственной теории изложенной в работе [1], допустили, что величина деформации в момент времени ![]() , возникающая за счет напряжений, действующих до момента времени
, возникающая за счет напряжений, действующих до момента времени ![]() , равна
, равна
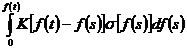 . (1)
. (1)
С учетом упругой деформации и выражения (1), интегральное уравнение связывающее деформацию и напряжение примет вид:
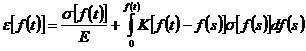 (2)
(2)
или
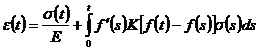 (3)
(3)
Уравнение (3) является линейным интегральным уравнением в преобразованной временной шкале относительно функции![]() с ядром ползучести
с ядром ползучести ![]() , а интегральное уравнение (2) является линейным уравнением в реальной временной шкале относительно функции
, а интегральное уравнение (2) является линейным уравнением в реальной временной шкале относительно функции ![]() с ядром ползучести
с ядром ползучести ![]() .
.
Исходя из представлений, что причиной релаксационных процессов является микроползучесть (такое представление определяет необходимость введения в математическое описание модели положения о независимости энергии активации ![]() от режимов деформирования, определяемое из экспериментов на ползучесть), и, учитывая активирующее действие напряжения на процесс деформации материала, интегральное уравнение (2) с ядром ползучести
от режимов деформирования, определяемое из экспериментов на ползучесть), и, учитывая активирующее действие напряжения на процесс деформации материала, интегральное уравнение (2) с ядром ползучести 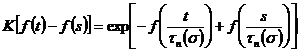 примет вид:
примет вид:
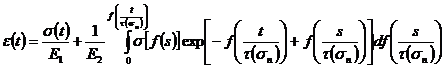 , (4)
, (4)
где ![]() и
и ![]() - упругие характеристики модели,
- упругие характеристики модели, ![]() и
и![]() - постоянные,
- постоянные, ![]() - деформация в момент времени
- деформация в момент времени ![]() ,
, ![]() - напряжение в момент времени
- напряжение в момент времени ![]() ,
, ![]() - напряжение, зависящее от текущего времени
- напряжение, зависящее от текущего времени ![]() ,
, ![]() - среднестатистическое время запаздывания, зависящее от напряжения
- среднестатистическое время запаздывания, зависящее от напряжения ![]() , определяемое из экспериментов на ползучесть,
, определяемое из экспериментов на ползучесть, ![]() - энергия активации,
- энергия активации, ![]() - сило-временной аргумент,
- сило-временной аргумент, ![]() .
.
Интегральное уравнение (4) в реальной временной шкале является интегральным уравнением с ядром ползучести ![]() .
.
Уравнение ползучести модели, которое вытекает из интегрального уравнения (4) при ![]() и вычисления интеграла стоящего в правой части уравнения (4) примет вид:
и вычисления интеграла стоящего в правой части уравнения (4) примет вид:
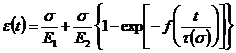 (5)
(5)
Индекс ![]() при напряжении
при напряжении ![]() в уравнении (5) опущен, так как рассматривается режим деформирования пряжи при постоянном напряжении.
в уравнении (5) опущен, так как рассматривается режим деформирования пряжи при постоянном напряжении.
Из уравнения ползучести (5) следует, что при ![]() ,
, ![]() - упругая деформация. При
- упругая деформация. При ![]() ,
, ![]() - предельная суммарная деформация.
- предельная суммарная деформация.
В работе [5], для количественного описания ползучести лавсановых нитей было применено уравнение ползучести с нормированной функцией арктангенс от степенного аргумента, которое имеет вид:
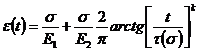 (6)
(6)
При 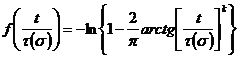 , где
, где ![]() ,
, ![]() и
и ![]() из уравнения (4) выводится уравнение (5).
из уравнения (4) выводится уравнение (5).
Уравнение (6) не применялось ранее для описания ползучести пряжи. Разрешая уравнение (4) относительно ![]() , получим интегральное уравнение с резольвентой
, получим интегральное уравнение с резольвентой ![]() , которое представим в виде:
, которое представим в виде:
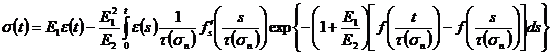 (7)
(7)
Из уравнения (7), при ![]() , выводится уравнение для описания релаксации напряжения модели в изотермических условиях испытания:
, выводится уравнение для описания релаксации напряжения модели в изотермических условиях испытания:
 (8)
(8)
При 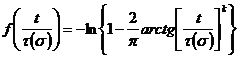 , уравнение (8) примет вид:
, уравнение (8) примет вид:
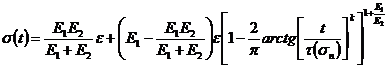 (9)
(9)
Следует отметить, что в уравнения (8) и (9) для описания релаксации напряжения входит время запаздывания ![]() , а не время релаксации
, а не время релаксации ![]() , определяемое из кривых релаксации напряжения.
, определяемое из кривых релаксации напряжения.
Представляет определенный интерес установление взаимосвязи времени запаздывания ![]() определяемого из кривых ползучести и временем релаксации напряжения
определяемого из кривых ползучести и временем релаксации напряжения ![]() , определяемого из кривых релаксации напряжения. Так как
, определяемого из кривых релаксации напряжения. Так как ![]() при применении уравнений (9) для описания релаксации напряжения является возрастающей функцией от времени, то для введения времени релаксации в уравнение (9), предположим, что время запаздывания связано со временем релаксации напряжения следующим равенством:
при применении уравнений (9) для описания релаксации напряжения является возрастающей функцией от времени, то для введения времени релаксации в уравнение (9), предположим, что время запаздывания связано со временем релаксации напряжения следующим равенством:
![]() , (10)
, (10)
где ![]() ,
, ![]() ,
, ![]() .
.
После подстановки (10) в (9) получим уравнение для описания релаксации напряжения пряжи, включающее в себя время релаксации напряжения, определяемое непосредственно из кривой релаксации напряжения:
 (11)
(11)
Из вывода уравнения (11) следует, что постоянная ![]() определенная из семейства кривых ползучести, должна превышать значение постоянной
определенная из семейства кривых ползучести, должна превышать значение постоянной ![]() определенной из кривых релаксации напряжения, то есть
определенной из кривых релаксации напряжения, то есть ![]() . Из последнего неравенства следует зависимость величины
. Из последнего неравенства следует зависимость величины ![]() и
и ![]() от режима нагружения.
от режима нагружения.
При применении уравнения (7) для описания релаксационных процессов в пряже при одностадийном ее нагружении в изотермических условиях, например, для описания семейства кривых релаксации напряжения или семейства диаграмм растяжения, величина времени запаздывания определяется из ![]() - той кривой ползучести соответствующей напряжению
- той кривой ползучести соответствующей напряжению ![]() . Поэтому, для описания кривых релаксации напряжения, соответствующих различным численным значениям деформации, при одностадийном нагружении пряжи или для описания диаграмм растяжения, соответствующих различным скоростям нагружения пряжи, должно выполняться равенство
. Поэтому, для описания кривых релаксации напряжения, соответствующих различным численным значениям деформации, при одностадийном нагружении пряжи или для описания диаграмм растяжения, соответствующих различным скоростям нагружения пряжи, должно выполняться равенство ![]() , где
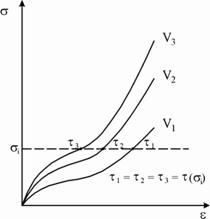
, где ![]() - определяется из экспериментов на ползучесть. На рис.1 отображено соответствие между временем запаздывания и напряжением для различных режимов нагружения пряжи.
- определяется из экспериментов на ползучесть. На рис.1 отображено соответствие между временем запаздывания и напряжением для различных режимов нагружения пряжи.
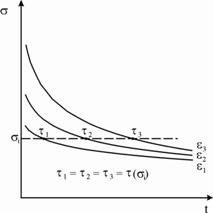
а) б)
Рис.1. Схематические изображения кривых релаксации напряжения и диа-
грамм растяжения и соответствие времен запаздывания: а) кривые
релаксации напряжения, ![]() ; б) диаграммы растяжения,
; б) диаграммы растяжения,
![]() .
.
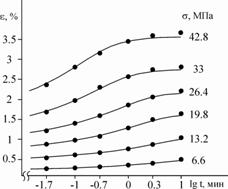
На рис.2а. приведены кривые ползучести исследуемой пряжи. Как следует из приведенного графика, семейство кривых ползучести в координатах ![]() характеризуется различными формами, включая
характеризуется различными формами, включая ![]() - образную форму.
- образную форму.
Для количественного описания семейства кривых ползучести применили уравнение (6). Численные значения упругих и вязких характеристик, входящие в (6) определяли графо-аналитическим методом с применением напряжено-временной аналогии [5]. Для определения упругих характеристик, входящих в уравнение (6), применялась методика, в основе которой лежит возможность построения обобщенной кривой. Для вычисления ![]() и
и ![]() были использованы выведенные формулы:
были использованы выведенные формулы:
 , (12)
, (12)
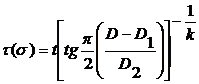 , (13)
, (13)
где ![]()
![]() ,
, ![]() .
.
Расчет ![]() проводился по формуле (13) при
проводился по формуле (13) при ![]()
На рис.2а приведены экспериментальные и расчетные кривые ползучести для пряжи. Расчетные кривые получены с применением уравнения (7). Из сопоставления экспериментальных и расчетных кривых наблюдается их хорошее соответствие.

а) б)
Рис.2 – кривые ползучести пряжи и зависимость ![]() от
от ![]()
а) - кривые ползучести; · - эксперимент, ¾¾ - расчет; б) зависимость ![]() от
от ![]() ;
;
Расчетные кривые ползучести для пряжи получены при значениях ![]() ,
, ![]() =
=![]() =0.319
=0.319 ![]() ,
,![]() =
=![]() =0.712
=0.712![]() и зависимости
и зависимости ![]() , приведенной на рис.2б. Численные значения характеристик вычислены с применением принципа напряженно-временной аналогии по методике приведенной в работе [5]. На рис.3 приведены диаграммы растяжения пряжи, соответствующие различным скоростям деформации.
, приведенной на рис.2б. Численные значения характеристик вычислены с применением принципа напряженно-временной аналогии по методике приведенной в работе [5]. На рис.3 приведены диаграммы растяжения пряжи, соответствующие различным скоростям деформации.
Для прогнозирования диаграмм растяжения по кривым ползучести использовалось уравнение, которое выводится из (7) при ![]() и
и ![]() с применением зависимости
с применением зависимости 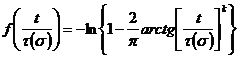 , где
, где ![]() и зависимость
и зависимость ![]() (рис. 2б) определяются из кривых ползучести.
(рис. 2б) определяются из кривых ползучести.
 , (14)
, (14)
где 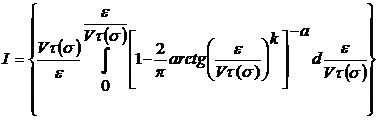 , (15)
, (15)
где ![]()

Рис.3 – Участки диаграмм растяжения соответствующие различным скоро-
стям деформации пряжи:
1 - V=0,0498 ![]() 2 - V=4.98
2 - V=4.98 ![]() ; ¾ - эксперимент, -·- и -│ё-
; ¾ - эксперимент, -·- и -│ё-
расчет.
Следует отметить, что в методологическом аспекте, из полученного уравнения для описания диаграммы растяжения рассчитывается величина деформации ![]() при заданной скорости деформации и известных значениях
при заданной скорости деформации и известных значениях ![]() , зависимости
, зависимости ![]() от
от ![]() , определяемых из экспериментов на ползучесть. После вычисления деформации производится построение графика в координатах
, определяемых из экспериментов на ползучесть. После вычисления деформации производится построение графика в координатах ![]() -
- ![]() . Для решения уравнения (14) написана специальная компьютерная программа.
. Для решения уравнения (14) написана специальная компьютерная программа.
Из сопоставления расчетных и экспериментальных диаграмм растяжения следует их достаточно хорошее соответствие (рис.3), что позволяет заключить о возможности применения предлагаемых интегральных уравнений, и соответственно разработанной методики для прогнозирования диаграмм растяжения пряжи по ее кривым ползучести.
Выводы
· Получены интегральные уравнения для описания нелинейной вязкоупругости пряжи с ядром ползучести ![]() и резольвентой
и резольвентой ![]() , с использованием положения о независимости энергии активации от режимов деформации при одностадийном нагружении пряжи до заданного напряжения.
, с использованием положения о независимости энергии активации от режимов деформации при одностадийном нагружении пряжи до заданного напряжения.
· На основе полученных интегральных уравнений разработана методика прогнозирования поведения пряжи под нагрузкой по кривым ползучести.
· Применимость разработанной методики прогнозирования показана на примере расчетов диаграмм растяжения пряжи по кривым ползучести.
ЛИТЕРАТУРА.
1. Малинин Н. Н. Прикладная теория пластичности и ползучести. – М. «Машиностроение», 1968 г. 400 c.
2. Сталевич А.М. // Проблемы прочности. 1981 г., ‡‚12, С. 95 – 98.
3. Сталевич А.М. // Известия вузов. ТЛП. – 1989 г., ‡‚ 3, С. 23 – 29.
4. Сталевич А.М. // Проблемы прочности, 1985 г., ‡‚2, С. 40-42.
5. Саркисов В.Ш., Автореферат диссертации на соискание ученой степени доктора технических наук. 2001г.
6. Бартенев Г.М., Зеленев Ю.В., Физика и механика полимеров-М. Высшая школа , 1983 г. 319 с.
7. Москин И.В., Бекина А.А., Саркисов В.Ш. // Известия ВУЗов, ТТП, 2007 г., ‡‚4, С. 109-113
Публикации с ключевыми словами: ползучесть, интегральные уравнения
Публикации со словами: ползучесть, интегральные уравнения
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



