научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 12, декабрь 2009
УДК: 62-408
kolobov@laspace.ru , victorfa@mail.ru
МГТУ им.Н.Э.Баумана
В массовом производстве контроль отклонений от цилиндричности и прямолинейности оси деталей типа валов можно осуществлять в автоматизированном режиме, используя сканирующие устройства, которые расположены в N сечениях по длине детали.
Оценим точность и методологию автоматизированного измерения отклонений от прямолинейности оси цилиндрических деталей на примере центрирования чурака в центрирующем загрузочном устройстве лущильного станка автоматической линии для производства фанерного шпона.
Назовем линию, проходящую через координаты центров поперечных сечений детали осью детали.
При сканировании поверхности детали в N сечениях по длине с последующим гармоническим анализом профиля поперечных сечений получаем массив из N эксцентриситетов поперечных сечений и массив фазовых углов эксцентриситетов. Эти два массива описывают положение в пространстве оси детали.
При простой кривизне в одной плоскости эта кривая представляет собой кривую второго порядка, расположенную в плоскости, проходящей через ось центров устройства проворота детали при сканировании. При сложной кривизне детали кривая будет описываться многочленом более высокого порядка.
Наиболее распространенным способом аппроксимации экспериментальных данных применяющимся в практике является метод наименьших квадратов, разработанный Гауссом.
Если при известном массиве пар экспериментальных данных ![]() ищется аппроксимирующая функция
ищется аппроксимирующая функция ![]() , то критерием выравнивания будет выражение
, то критерием выравнивания будет выражение
![]() .
.
При выравнивании прямыми ![]() необходимым и достаточным условием того, чтобы точки массива экспериментальных данных
необходимым и достаточным условием того, чтобы точки массива экспериментальных данных ![]() лежали на прямой, является пропорциональность разностей
лежали на прямой, является пропорциональность разностей ![]() и
и ![]() (i = 2, 3,…n), т.е.
(i = 2, 3,…n), т.е. ![]() .
.
При использовании для записи выражений суммирования ![]() выражения для определения коэффициентов a и b прямой имеют вид
выражения для определения коэффициентов a и b прямой имеют вид
![]()
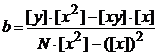
Оценим точность аппроксимации реальной оси чурака прямой линией, параметры которой определены методом наименьших квадратов (по алгоритму Гаусса).
Оценку проводим для чурака круглого сечения с осью, лежащей в одной плоскости. По ГОСТ 9462-88 допускается величина простой кривизны детали 2-го сорта до 3% от длины чурака. При длине чурака 1600мм максимальная кривизна составит 48мм.
В первом приближении принимаем, что реальная ось чурака описывается синусоидой. При простой кривизне чурака можно рассматривать плоскую задачу, ограничиваясь аппроксимацией, например, в плоскости XZ.
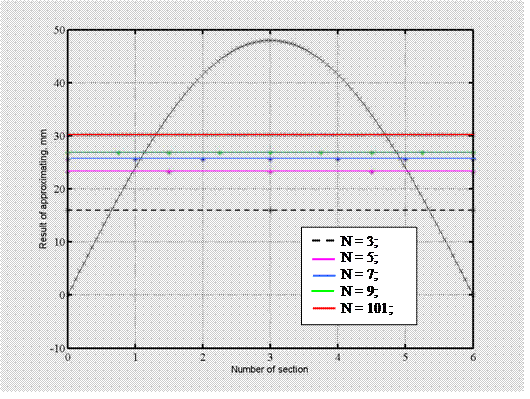
На рисунке 1 представлены результаты аппроксимации синусоидальной оси детали прямой линией при различном числе сканируемых сечений по длине. Для простоты сечения равномерно располагаются по длине чурака.
 |
||
|
Рис.1. Аппроксимирующие прямые осевой линии детали при различном числе сечений сканирования |
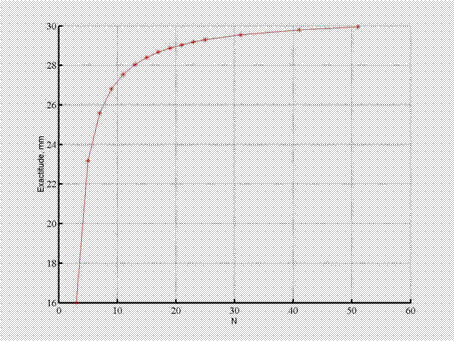
Численные значения эксцентриситета аппроксимирующей прямой относительно оси проворота детали приведены в таблице 1.
Таблица 1
|
N |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
|
e, мм |
16.0 |
23.17 |
25.59 |
26.81 |
27.55 |
28.04 |
28.40 |
|
N |
17 |
19 |
21 |
23 |
31 |
41 |
51 |
|
e, мм |
28.66 |
28.87 |
29.04 |
29.17 |
29.54 |
29.79 |
29.94 |
График динамики сходимости метода представлен на рисунке 2.
|
|
|
Рис.2. Динамика сходимости метода аппроксимации осевой линии детали прямой в зависимости от числа N сечений сканирования |
При круглом сечении и искривлении оси детали по синусоидальному закону диаметр фанерной зоны равен ![]() (см. рис.3), а оптимальная коррекция оси детали – 0,5е.
(см. рис.3), а оптимальная коррекция оси детали – 0,5е.
|
|
|
Рис.3. Уменьшение фанерной зоны при искривлении оси детали. |
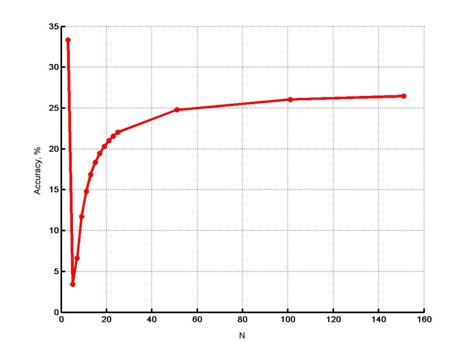
График погрешности метода представлен на рисунке 4. За точное значение положения аппроксимирующей прямой относительно оси проворотного устройства (или оси лущильного станка) принято значение, равное 0,5е.
|
|
|
Рис.4. Зависимость точности аппроксимации от количества сечений N по длине детали |
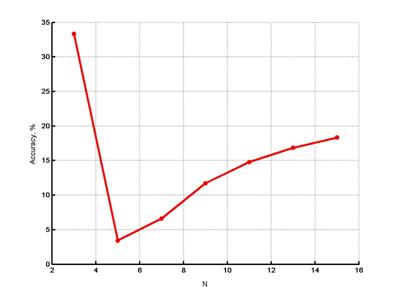
Эта же зависимость в более крупном масштабе представлена на рисунке 5.
|
|
|
Рис.5. Зависимость точности аппроксимации от количества сечений N по длине детали для 3£N£15 |
Из графиков видно, что зависимость точности аппроксимации оси детали прямой линией методом наименьших квадратов от количества сканирующих устройств имеет экстремум, соответствующий 5 сканирующим устройствам. Погрешность метода при этом составляет около 3,4%.
При неравномерном расположении сканирующих головок по длине детали точность метода можно повысить. Покажем это на примере сканирования 5 лазерными головками.
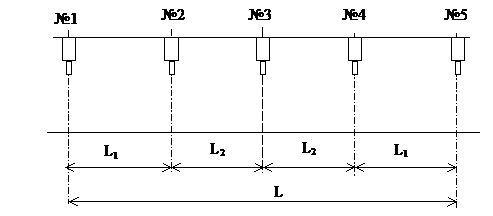
Сместим головки ╧2 и ╧4 от середины детали (см. рис.6).
|
|
|
Рис.6. Схема размещения сканирующих головок |
Коэффициент смещения ![]() .
.
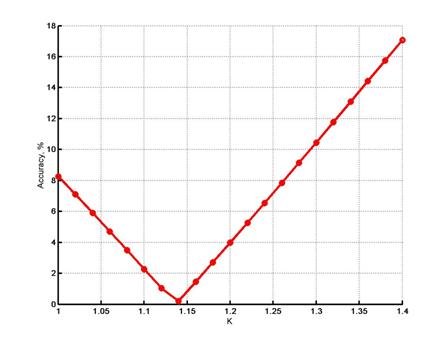
График зависимости погрешности метода оптимизации от величины коэффициента смещения представлен на рисунке 7.
|
|
|
Рис.7. Зависимость ошибки оптимизации от величины коэффициента смещения К для 5 сканирующих устройств |
Зависимость имеет минимум, равный 0,2% при К = 1,14.
Литература:
1. Справочник по математике для инженеров и учащихся втузов. Бронштейн И.Н., Семендяев К.А. –М.: Наука. 1981.
2. ГОСТ 9462-88 Лесоматериалы круглые лиственных пород. Технические условия.
Публикации с ключевыми словами: автоматизированные измерения
Публикации со словами: автоматизированные измерения
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||