научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 12, декабрь 2009
УДК 621.941.1
.
e-mail: grusv@yandex.ru
МГТУ им. Н.Э. Баумана
Кафедра "Инструментальная техника и технологии"
Статья подготовлена по результатам работ, проведенных в рамках проекта Российского фонда фундаментальных исследований ╧07-08-92103
Современные наукоемкие машины и приборы характеризуются ростом требований по точности и качеству составляющих деталей. Например, предельные требования по макроотклонениям для поверхностей оптических элементов, входящих в лазерные резонаторы и системы транспортировки и фокусировки излучения, определяются типом лазера, длиной волны излучения l и составляют:
- непрерывный режим работы (l = 10,6 мкм) - l/5÷l/10;
- непрерывный или импульсный (l = 2,6÷3,6 мкм) - l/15÷l/20;
- импульсный (l = 0,13÷0,35 мкм) - l/40÷l/50.
Отражательная способность металлооптической поверхности должна характеризоваться коэффициентом зеркального отражения до 0,99 и выше, коэффициентом поглощения менее 0,01, и следует учитывать, что диффузная составляющая отражения пропорциональна величине (Rq/l)2, где Rq – средняя квадратичная величина шероховатости.
Наиболее широкое применение металлические зеркала находят в лазерных технологических установках, предназначенных для резки, сварки, закалки и других технологических процессов. В этом случае усредненные технические требования к металлическим отражателям составляют: отклонение формы N = 2 интерференционных кольца (N = 0,55 мкм) на диаметре пробного стекла, местная ошибка DN = 0,3 интерф. кол., средняя квадратичная величина шероховатости менее 12 нм, отклонение радиуса сферической поверхности от номинала менее 1%, коэффициент зеркального отражения более 0,97, местная тепловая деформация поверхности при эксплуатации не более 1 мкм, ресурс работы не менее 100 часов.
Традиционным методом чистовой обработки металлооптических элементов являются чистовое шлифование и окончательное полирование свободным абразивом, что позволяет достичь наилучшего прилегания обрабатываемой поверхности к идеальной сферической или плоской поверхности. По существу метод основан на взаимном притирании инструмента и детали через слой абразивной суспензии. Инструментом служит полировальник с рабочим слоем из полировальной смолы. Предельно высокая точность обработки в этом случае достигается за счет многократной правки полировальника и перенастройки станка, и во многом зависит от квалификации полировщика. Помимо этого на качество поверхностного слоя отрицательно влияет шаржирование микрометрическими абразивными частицами и загрязнение поверхности полировальным составом. Трудоемкость полирования возрастает при обработке крупногабаритных и в особенности асферических металлооптических поверхностей, и может составить десятки и сотни часов.
В последние десятилетия находит развитие и применение метод лезвийной обработки – алмазное точение (АТ или "микроточение" – АМТ), как метод автоматизированной обработки поверхностей металлооптики алмазными монокристаллическими резцами на специальных особо точных станках. Основное преимущество метода заключается в существенном увеличении производительности по сравнению с традиционными методами, в особенности при обработке крупногабаритных, асферических поверхностей и металлических зеркал сложной формы для высокоэнергетических лазерных установок. Поверхностный слой после алмазного точения имеет повышенное качество и лучшее металлографическое состояние, чем полированный, а оптические поверхности – более высокий порог разрушения под действием лазерного излучения.
Кинематическая схема АТ металлооптических поверхностей приведена на рис. 1. На кинематической схеме показано, что заготовка вращается вокруг оси О1 с частотой вращения w, обеспечивая главное движение резания Dr . Резец находится в относительном движении подачи, перемещаясь по дуге окружности радиуса Rc относительно центра О2 со скоростью vc , град/с, обеспечивая вспомогательное движение подачи Ds . Каждый станок характеризуется своим значением кинематического параметра Rc, а также максимальным значением радиуса R0 обрабатываемой поверхности.
|
|
|
Рис. 1. Кинематическая схема алмазного точения на сверхточном станке |
В расчетной части модели общая схема косоугольного несвободного резания для резца с радиусной вершиной представлена схемой обобщенного плоского состояния в направлении схода стружки – рис. 2.
|
|
|
Рис. 2. Схема косоугольного несвободного резания при алмазном точении |
Угол действия wd и коэффициент утолщения (усадки) определены через известные выражения:
![]() ,
, ![]() ,
,
где ![]() - угол сдвига, передний и задний углы в направлении схода стружки.
- угол сдвига, передний и задний углы в направлении схода стружки.
Сила стружкообразования, действующая в условной плоскости сдвига, равна
 ,
,
где tp – касательные напряжения в плоскости сдвига, ![]() - эффективная (средняя) толщина и ширина срезаемого слоя.
- эффективная (средняя) толщина и ширина срезаемого слоя.
Отсюда следуют выражения для расчета сил на передней поверхности инструмента (рис. 2):
![]() - трения;
- трения;
![]() - нормальная;
- нормальная;
![]() ,
, ![]() - составляющие тангенциальная и нормальная в системе координат
- составляющие тангенциальная и нормальная в системе координат![]() ;
;
![]() ,
, ![]() ,
,
(1)
![]() - составляющие силы резания в системе координат
- составляющие силы резания в системе координат ![]() .
.
На задней поверхности определены силы:
- нормальная ![]() ,
,
- тангенциальная ![]() ,
,
где ![]() – длина контакта по задней поверхности инструмента.
– длина контакта по задней поверхности инструмента.
Величина коэффициента трения на задней поверхности алмазного резца определяется в основном молекулярной составляющей и находится в пределах 0,06 ÷ 0,07.
Тогда суммарные силы, действующие на резец со стороны передней и задней поверхностей в направлении осей координат ![]() равны сумме соответствующих составляющих:
равны сумме соответствующих составляющих:
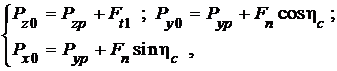 (2)
(2)
где силы на передней поверхности рассчитаны по (1).
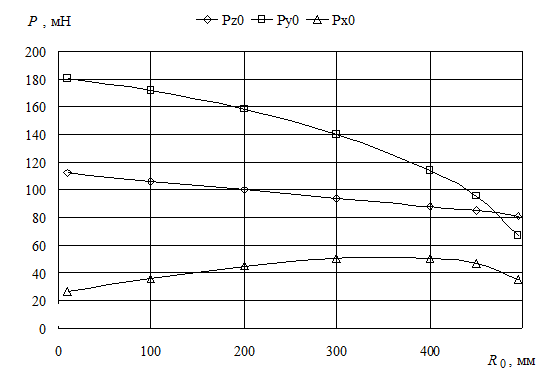
Расчеты показывают, что составляющие силы резания изменяются при движении резца от периферии к центру вращения заготовки, причем значительно возрастает радиальная составляющая Py0 вследствие изнашивания резца – рис. 3. Следует обратить внимание на малую величину сил резания при АТ, которые изменяются в пределах от десятых до сотых долей Ньютона. Вместе с тем, учитывая жесткие требования, предъявляемые на операции АТ к значениям допустимых макроотклонений обрабатываемых поверхностей, деформация технологической системы под действием сил резания может иметь существенное значение.
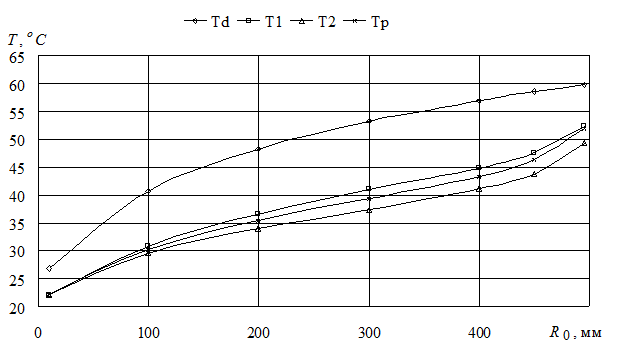
Рассчитаны параметры, характеризующие тепловую напряженность процесса: температура деформации Td , средние температуры на передней T1 и задней T2 поверхностях, средняя температура резания Tp. Изменение температуры деформации, температур на контактных поверхностях, температуры резания при обработке алюминиевой поверхности и движении резца от периферии к центру в зависимости от текущего радиуса показано на рис. 4 (все расчетные температуры прибавлены к температуре окружающей среды 20 оС).
|
|
|
Рис. 3. Изменение составляющих силы при обработке алюминиевой поверхности от периферии к центру заготовки; t = 4 мкм, w = 150 об/мин, vs = 1,37 мм/мин |
|
|
|
Рис. 4. Изменение температур при точении алюминиевой поверхности от периферии к центру; t = 4 мкм, w = 150 об/мин, vs = 1,37 мм/мин |
Анализ результатов расчетов подтверждает, что низкие значения сил резания и коэффициента трения определяют малую тепловую напряженность зоны резания. Так, температура резания даже для периферийной зоны поверхности диаметром 1000 мм не превышает 60 оС.
При анализе тепловых деформаций инструмента принято допущение, что термоупругие напряжения в рабочей части резца пренебрежимо малы и взаимовлияние термоупругих перемещений инструментального материала в различных направлениях несущественно. Тогда основное изменение размеров рабочей части резца происходит по закону линейного расширения. Закон распределения температуры по длине инструмента в момент времени t составит
![]() ,
,
где безразмерная функция, характеризующая закон распределения температуры по длине инструмента, имеет вид:
 ,
,
![]() - коэффициент температуропроводности инструментального материала,
- коэффициент температуропроводности инструментального материала, ![]() - время, прошедшее с начала процесса резания, Tp – температура резания.
- время, прошедшее с начала процесса резания, Tp – температура резания.
Общее удлинение рабочей части резца, жестко закрепленного в державке с вылетом ![]() , в момент времени t составит:
, в момент времени t составит:
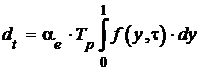 , или
, или ![]() ,
,
где функция  задана графиком [2],
задана графиком [2], ![]() - безразмерная длина,
- безразмерная длина, 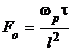 - критерий Фурье, ae – эквивалентный коэффициент линейного расширения для алмаза и материала державки, h1 – длина алмаза, h2 – длина державки от опоры. Текущее время равно
- критерий Фурье, ae – эквивалентный коэффициент линейного расширения для алмаза и материала державки, h1 – длина алмаза, h2 – длина державки от опоры. Текущее время равно 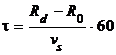 , где Rd – наибольший радиус поверхности, R0 – текущий радиус обработки.
, где Rd – наибольший радиус поверхности, R0 – текущий радиус обработки.
Анализ величины тепловой деформации алмазного резца показывает, что она может составлять существенное значение при обработке крупногабаритной поверхности, а снижение тепловой деформации возможно за счет уменьшения вылета инструмента и замены материала державки на инвар, имеющий коэффициент линейного расширения, близкий к алмазу.
При анализе общего макроотклонения ![]() обработанной поверхности учтены составляющие:
обработанной поверхности учтены составляющие:
- деформации технологической системы под действием радиальной составляющей силы ![]() где j - жесткость технологической системы;
где j - жесткость технологической системы;
- hr – радиальный износ резца;
- dt – тепловая деформация (удлинение) резца.
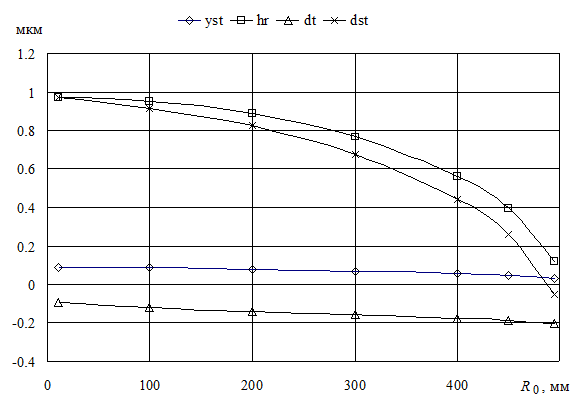
На рис. 5 приведены графики составляющих и общей погрешности обработки dst в зависимости от текущего радиуса при обработке поверхности диаметром 1000 мм. Установлено преобладающее влияние радиального износа и теплового удлинения резца на погрешность обработки. С увеличением жесткости до значения 20 Н/мкм и более деформация технологической системы практически не оказывает влияния на общую погрешность обработки.
|
|
|||
|
Рис. 5. Влияние текущего радиуса заготовки на составляющие погрешности при алмазном точении алюминиевой поверхности от периферии к центру; t = 4 мкм, w = 150 об/мин, vs = 1,37 мм/мин, j = 2 Н/мкм |
На основании проведенного анализа отмечена возможность достижения высокой точности обработки крупногабаритных поверхностей (в приведенном примере расчетные макроотклонения поверхности диаметром 1000 мм составляют менее 1,0 мкм).
Следует отметить возможность существенного увеличения погрешностей при прерывистом характере обработки, например, при внеосевом расположении заготовок на планшайбе станка.
Процесс резания при прерывистом характере обработки имеет особенности, оказывающие существенное влияние на макроотклонения обработанной поверхности. Количественный анализ проведен для случая внеосевого расположения трех деталей радиусом Rd = 203 мм на планшайбе станка как показано на рис. 6. Рассмотрен общий случай колебания технологической системы с одной степенью свободы около положения устойчивого равновесия, когда на приведенную массу действуют силы: возмущающие, восстанавливающие и сопротивления. Под возмущающей силой понимается сила резания, действующая во время контакта резца с обрабатываемой поверхностью. Переходные процессы во время врезания и выхода резца из контакта с заготовкой не существенны в связи с малыми величинами снимаемого припуска и сечения срезаемого слоя.
Уравнение колебаний, вызванных постоянной обобщенной силой, приложенной к системе и действующей в течении некоторого промежутка времени ![]() контакта резца с заготовкой имеет вид
контакта резца с заготовкой имеет вид
![]()
или
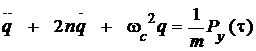 , (3)
, (3)
где  - коэффициент инерции (приведенная масса);
- коэффициент инерции (приведенная масса); ![]() – круговая собственная частота незатухающих колебания;
– круговая собственная частота незатухающих колебания; ![]() - коэффициент демпфирования или
- коэффициент демпфирования или ![]() ;
; ![]() - безразмерный коэффициент затухания. Для обработки деталей по схеме рис. 6 частота круговых колебаний будет составлять
- безразмерный коэффициент затухания. Для обработки деталей по схеме рис. 6 частота круговых колебаний будет составлять ![]() , где w - частота вращения шпинделя, об/мин; kd = 3 – число деталей на планшайбе.
, где w - частота вращения шпинделя, об/мин; kd = 3 – число деталей на планшайбе.
|
|
|
Рис. 6. Схемы прерывистого АТ трех внеосевых поверхностей, импульсов силы и деформации технологической системы |
В соответствии с технологической схемой обработки kd – деталей расположены на планшайбе станка, центры деталей находятся на радиусе ![]() относительно центра вращения. Вращение планшайбы задает главное движение резания Dr, движение подачи Ds имеет резец по дуге окружности радиуса Rc .
относительно центра вращения. Вращение планшайбы задает главное движение резания Dr, движение подачи Ds имеет резец по дуге окружности радиуса Rc .
В соответствии со схемой действия импульсов сил и деформаций технологической системы при контакте резца с каждой заготовкой начальные условия по деформации и скорости деформации приведенной массы имеют вид: ![]() ;
; ![]() - на первом импульсе;
- на первом импульсе; ![]() ;
; ![]() - на последующих импульсах, когда возмущающая сила начинает действовать в момент времени t1 , равном периоду на текущем радиусе обработки R0. Общее решение дифференциального уравнения (3) в случае малого сопротивления могут быть найдены по известным из теории колебаний соотношениям. Разработанная программа AT_din осуществляет расчет деформации и скорости деформации по всем импульсам, начиная с первого на радиусе обработки
- на последующих импульсах, когда возмущающая сила начинает действовать в момент времени t1 , равном периоду на текущем радиусе обработки R0. Общее решение дифференциального уравнения (3) в случае малого сопротивления могут быть найдены по известным из теории колебаний соотношениям. Разработанная программа AT_din осуществляет расчет деформации и скорости деформации по всем импульсам, начиная с первого на радиусе обработки ![]() и оканчивая последним на радиусе
и оканчивая последним на радиусе ![]() .
.
В качестве примера на рис. 7 показаны расчетные значения деформаций технологической системы для текущего радиуса обработки ![]() мм. Исходные данные для расчетов были приняты: глубина резания
мм. Исходные данные для расчетов были приняты: глубина резания ![]() мкм, подача
мкм, подача ![]() мкм/об, частота вращения шпинделя станка
мкм/об, частота вращения шпинделя станка ![]() мин –1, коэффициент затухания
мин –1, коэффициент затухания ![]() , жесткость
, жесткость ![]() Н/мкм, приведенная масса
Н/мкм, приведенная масса ![]() Нс2/м. Для этих условий значения частот колебаний составили, с -1: круговой
Нс2/м. Для этих условий значения частот колебаний составили, с -1: круговой ![]() , собственной
, собственной ![]() .
.
Общее макроотклонение в каждой расчетной точке по обрабатываемой поверхности помимо деформации технологической системы также учитывает радиальный износ и тепловую деформацию резца: ![]() . Тогда общая погрешность обработки по всей поверхности составляет сумму минимального и максимального макроотклонений по всем расчетным точкам:
. Тогда общая погрешность обработки по всей поверхности составляет сумму минимального и максимального макроотклонений по всем расчетным точкам: ![]() .
.
|
|
|
Рис. 7. Графики, иллюстрирующие аналитическое решение дифференциального уравнения вынужденных колебаний технологической системы; текущий радиус обработки |
Дифференциальное уравнение (3) помимо аналитического решения может иметь решение путем моделирования в компьютерной системе MATLAB – SIMULINK [3]. На рис. 8 показана визуализация процесса решения с приведенными выше исходными данными. Здесь задан источник импульсного сигнала радиальной составляющей силы ![]() Н длительностью
Н длительностью ![]() с и периодом
с и периодом ![]() с, соответствующий текущему радиусу обработки
с, соответствующий текущему радиусу обработки ![]() мм. Начальные условия приняты: по деформации
мм. Начальные условия приняты: по деформации ![]() м, по скорости деформации
м, по скорости деформации ![]() м/с. Процесс построения модели представляет последовательность выбора необходимых блоков из соответствующих библиотек и соединение их связями.
м/с. Процесс построения модели представляет последовательность выбора необходимых блоков из соответствующих библиотек и соединение их связями.
|
|
|
Рис. 8. Simulink- модель решения дифференциального уравнения вынужденных колебаний |
На схеме рисунка показаны блоки:
- сумматор, имеющий три входа, соответствующих правой части преобразованного уравнения (3) ![]() ;
;
- два интегратора "1/s", на выходе которых получают значения первой производной и самой деформации;
-осциллограф "Scope" - позволяет графически представить возмущающую силу, скорость деформации и деформацию технологической системы как функции времени;
- графопостроитель "XYGraph" - позволяет получить фазовую траекторию решения дифференциального уравнения.
Характерно, что полученные деформации путем моделирования практически соответствуют оптимальному решению, представленному в виде графиков на рис. 7. Simulink- модель легко позволяет проследить влияние исходных данных (приведенной массы, жесткости, коэффициента демпфирования) на деформацию технологической системы.
Графики составляющих и общей погрешности обработки алюминиевых отражателей по схеме рис. 6 приведены на рис. 9 в зависимости от текущего радиуса обработки (резец движется от периферии к центру вращения заготовки). Здесь общая погрешность обработки по всей поверхности составляет ~ 2040 нм.
|
|
|
Рис. 9. Графики составляющих и общей погрешности обработки алюминиевых отражателей: 1 – тепловое удлинение резца; 2 – статическая деформация технологической системы; 3 – радиальный износ резца; 4 – общая погрешность обработки |
По результатам проведенного анализа намечены пути снижения макроотклонений обработанных АТ металлооптических поверхностей: рациональный выбор параметров, характеризующих технологическую систему; использование кристаллов алмазов повышенного качества и размеров, обеспечивающих повышение износостойкости алмазных резцов и снижение величины радиального износа инструмента; применение материалов и конструкций инструмента, обеспечивающих снижение тепловых деформаций; управление режимными параметрами и коррекция текущей погрешности с использованием системы управления станком в режиме реального времени.
Список литературы
1. Дун Гоцзюнь, С.В. Грубый. Анализ закономерностей процесса алмазного точения и точности обработки поверхностей металлооптики/ Технология металлов, 2008, ╧2, с. 26-32.
2. Резников А.Н., Резников Л.А. Тепловые процессы в технологических системах. - М.: Машиностроение, 1990. – 288 с.
3. Мещеряков В.В. Задачи по математике с MATLAB & SIMULINK. – М.: ДИАЛОГ –МИФИ. 2007. – 528 с.
4. Программа для ЭВМ "RegAMT (Алмазное точение (АТ) металлооптических элементов. Параметры процесса, погрешности обработки)". – Регистрационное свидетельство МНИИ "Интеграл" ╧0000430 от 18.11.2009 г.
5. Программа для ЭВМ "AT_din (Прерывистое алмазное точение поверхностей металлооптики (АТ), расчет импульсов, расчет погрешностей обработки)". – Регистрационное свидетельство МНИИ "Интеграл" ╧0000428 от 18.11.2009 г.
Публикации с ключевыми словами: алмазное точение, металлооптика
Публикации со словами: алмазное точение, металлооптика
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||