научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2009
Московский Государственный Университет Прикладной Биотехнологии,
109316, Москва, ул. Талалихина, дом 33.
zhirkovandrew@gmail.com
Введение
Современные рыночные условия становятся все более жесткими для предприятий. Требования потребителей постоянно растут, и предприятиям приходится особое внимание уделять ассортименту и качеству производимой продукции. Широкий ассортимент, низкие цены и хорошее качество продукции - это конечный результат эффективности воспроизводства основных фондов и как следствие залог успеха любого предприятия.
Важную роль играют внутренние факторы воспроизводства основных фондов. Они зависят от принятой учетной политики на предприятиях, от принятых методов амортизации, от уровня квалификации персонала и т.д. В современных быстроразвивающихся условиях, конечно же, более эффективной будет политика направленная на ускоренную амортизацию. Так, в развитых странах средний срок полного обновления основного капитала не превышает 15 - 20 лет, причем в США срок обновления активной части основного капитала составляет 12 - 14 лет, а в Японии - 8 - 10 лет из-за более облегченной структуры воспроизводства, специализированной на информационных и наукоемких технологиях. В СССР средний срок обновления основных производственных фондов равнялся 20 - 25 годам [6]. Анализ существующих подходов к управлению процессом воспроизводства основных фондов показал, что до сих пор существует ряд нерешенных проблем.
Воспроизводство с целью повышения экономического положения предприятия - это капитальные вложения на замену изношенных основных средств необходимые в связи с тем, что с течением времени основные средства физически изнашиваются, и соответственно снижается объем и качество выпускаемой продукции, производительность труда, увеличиваются простои машин и оборудования. С целью их сохранения, хотя бы на первоначальном уровне, предприятию необходимо периодически осуществлять вложения в модернизацию, среднесрочный и капитальный ремонт машин и оборудования, реконструкцию производства, замену физически непригодных основных средств. К примеру, режим простого воспроизводства можно организовать без внешних инвестиций и только на определенную часть от прибыли, полученную от деятельности предприятия.
Производственная функция простого режима воспроизводства предприятия
В процессе производства, с одной стороны, осуществляются капиталовложения и ввод основных производственных фондов (ОПФ) в эксплуатацию. Этим процессом обусловлено увеличение количества производственных фондов. С другой стороны, происходит уменьшение производственных фондов в результате амортизации и выбытия. Если в качестве модели движения производственных фондов принять инерционное звено первого порядка, у которого внешнее воздействие I(t) – интенсивность потока капиталовложений, S(t) – интенсивность потока амортизации и T – лаг эксплуатации производственных фондов, тогда текущая стоимость производственных фондов определяется операторным уравнением (применение метода преобразования Лапласа [5]):
![]() , (1)
, (1)
где F0 – начальная стоимость производственных фондов.
Запишем изображение процесса амортизации в виде:
![]() , (2)
, (2)
то есть амортизация пропорциональна текущей стоимости производственных фондов и составляет постоянную ее долю. Доля амортизированных фондов n – норма амортизации. Подставив реакцию A(s) в (1) и решив это уравнение относительно F(s), получим следующую зависимость накопленного количества производственных фондов от капиталовложений:
![]() . (3)
. (3)
Предположим теперь, что производственная функция зависит только от стоимости производственных фондов, то есть является однофакторной. В данном случае абстрагируемся от трудовых ресурсов и прочих параметров, так как они не влияют на окончательный результат. Запишем однофакторную динамическую производственную функцию сельхозпредприятия:
![]() , (4)
, (4)
где m – фондоотдача.
Подставив в (4) полученное выражение (3), получим зависимость интенсивности выпуска от интенсивности потока капиталовложений в операторной форме:
![]() ,
, ![]() , (5)
, (5)
где F(s) – передаточная функция производственной функции простого режима воспроизводства предприятия.
Математическая модель простого режима воспроизводства предприятия
В синтезе модели отдельного предприятия будем исходить из того, что объем произведенной и реализованной продукции зависит от остаточной стоимости ОПФ, которая может увеличиваться или уменьшаться. Она возрастает в зависимости от капиталовложений и уменьшается в результате амортизации и выбытия некоторой части основных средств. Следовательно, рост объемов выпуска может быть обеспечен в том случае, если капиталовложения превышают количество изношенных ОПФ, тогда и текущая их стоимость увеличивается. При снижении стоимости ОПФ рост объема выпуска может быть достигнут за счет повышения фондоотдачи, то есть влияния научно-технического прогресса. Эти явления отражает модель производства в виде однофакторной динамической производственной функции.
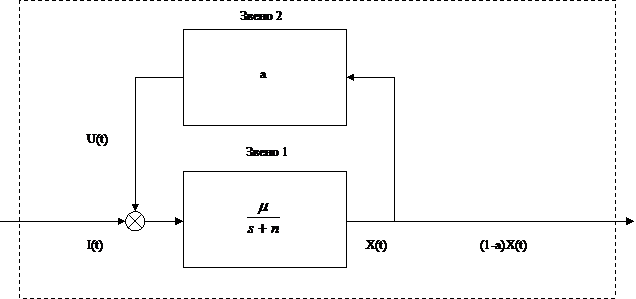 Капиталовложения слагаются из централизованных средств I(t) и отчислений от дохода U(t). Предположим, что отчисления регламентируются нормативом a < 1. Тогда функциональную структуру развития предприятия можно представить в виде модели с положительной обратной связью, состоящей из двух звеньев. Усилительное звено 2 отражает процесс выделения собственных капиталовложений при нормативе отчислений от объема реализации продукции a. Вместе с централизованными капиталовложениями собственные средства воздействуют на звено производства 1, изменяя стоимость ОПФ и объем дохода от реализации продукции X(t) в виде динамической производственной функции.
Капиталовложения слагаются из централизованных средств I(t) и отчислений от дохода U(t). Предположим, что отчисления регламентируются нормативом a < 1. Тогда функциональную структуру развития предприятия можно представить в виде модели с положительной обратной связью, состоящей из двух звеньев. Усилительное звено 2 отражает процесс выделения собственных капиталовложений при нормативе отчислений от объема реализации продукции a. Вместе с централизованными капиталовложениями собственные средства воздействуют на звено производства 1, изменяя стоимость ОПФ и объем дохода от реализации продукции X(t) в виде динамической производственной функции.
Рис.1.
Чтобы найти передаточную функцию системы необходимо разрешить следующую систему уравнений относительно X(s):
 (6)
(6)
где n – норма амортизации,
F0 – начальное значение стоимости ОПФ,
m – фондоотдача в единицах измерения остаточной стоимости ОПФ,
a – норматив отчислений в фонд развития производства,
n – норма амортизации.
В результате получим:
![]() , (7)
, (7)
где первое слагаемое – вынужденная, а второе – свободная составляющая; x0 – начальное значение интенсивности производства и реализации продукции. Передаточная функция системы равна ![]() .
.
Структура системы с такой передаточной функцией показана на рис.1.
Заключение
Получена математическая модель простого режима воспроизводства предприятия. Данная модель развития предприятия пригодна для анализа сложных систем, в которые эта модель может входить как составной элемент.
Литература
1. Кибернетика: прошлое для будущего., М.: Наука, 1989. – (Серия «Кибернетика – неограниченные возможности и возможные ограничения»), 135 с.
2. Кибернетика. Современное состояние., М.: Наука, 1980. – (Серия «Кибернетика – неограниченные возможности и возможные ограничения») , 72 с.
3. Неймарк Ю.И. Математические модели естествознания и техники. Нижний Новгород: ННГУ, 1994. Вып. 1. 83 с.; 1996. Вып. 2. 154 с.
4. Н.П. Бутов, д.т.н. ВНИПТИМЭСХ, В.Н. Чекарь, инженер АЧГАА, «Экономико-математическая модель оптимизации дилерского предприятия»,УДК 631.173.6, г. Зеленоград, журнал "Механизация и электрификация сельского хозяйства" ╧2 2001г.
5. http://ru.wikipedia.org/wiki/Преобразование_Лапласа
6. Новицкий И. Выбор инвестиционной стратегии на новом этапе реформ // Экономист. 2001. ╧ 6
Публикации с ключевыми словами: математическая модель, передаточная функция
Публикации со словами: математическая модель, передаточная функция
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



