научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 10, октябрь 2009
Россия, Москва,
Московский Авиационный Институт
dyanishev@list.ru
Введение
Расчеты нестационарных тепловых и гидродинамических процессов становятся в ряд определяющих при разработке новых образцов техники в различных областях - в двигателестроении, авиации и космонавтике, энергетике, судостроении, криогенной технике, химической технологии и т. д.
Экспериментальные и теоретические исследования показывают существенное отличие коэффициентов теплоотдачи и гидродинамического сопротивления в нестационарных условиях от данных квазистационарного расчета. Оно может достигать 3-х - 4-х кратного значения. Под квазистационарным расчётом здесь и далее будем понимать расчёт с использованием эмпирических зависимостей, полученных для стационарных условий.
-
Анализ экспериментальных данных
К настоящему времени накоплены значительные экспериментальные данные по нестационарным турбулентным потокам в каналах. Данные Э.К. Калинина и д.р. [1], С.Б. Маркова [2], Г.А. Дрейцера и В.М. Краева [3] показали, что при ускорении течения профиль скорости становится более заполненным у стенки и менее заполненным у оси. При замедлении течения наблюдается обратная картина. Качественно это показано на Рис. 1.

Рис. 1. Качественное изменение профиля скорости при ускорении и замедлении потока в трубе по данным [1].
Профиль турбулентной вязкости при ускорении и замедлении изменяется подобным образом (см. Рис. 2).

Рис. 1. Качественное изменение профиля турбулентной вязкости при ускорении и замедлении потока в трубе по данным [1].
Экспериментально авторами [3] было установлено, что замедление потока приводит к увеличению по сравнению с квазистационарными значениями коэффициента трения (гидродинамического сопротивления) ξ и числа Nu. Замедления течения приводит к противоположному результату.
В качестве основного критерия, характеризующего нестационарность течения в [3] был принят:
 (1)
(1)
В качестве временного параметра был выбран приведённый критерий гомохронности Ho.
 (2)
(2)
где ![]() соответствует текущему времени процесса, а Ho0- общему времени процесса.
соответствует текущему времени процесса, а Ho0- общему времени процесса.
Экспериментальные данные по изменению коэффициента трения ξ и числа Nu для различных значений Kg* представлены на Рис. 3-6.
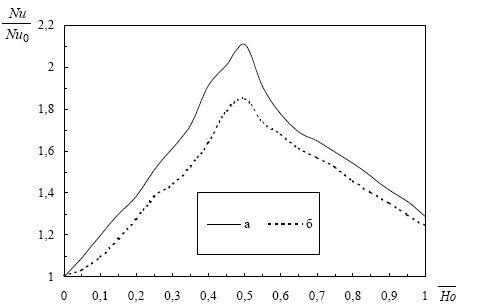
Рис. 3. Влияние ускорения течения на теплообмен, Re=3100…9300, Tw/Tf=1.18, а- Kg*max =0.111, б- Kg*max =0.088.

Рис. 4. Влияние замедления течения на теплообмен, Re=3100…9300, Tw/Tf=1.18, а- Kg*min = -0.111, б- Kg*min = -0.044.

Рис. 5. Влияние ускорения течения на коэффициент трения, Re=3100…9300, Tw/Tf=1, а- Kg*max =0.111, б- Kg*max =0.088.

Рис. 6. Влияние замедления течения на коэффициент трения, Re=3100…9300, Tw/Tf=1, а- Kg*min = -0.111, б- Kg*min = -0.044.
Также авторами [3] было установлено, что повышения числа Рейнольдса снижает влияние ускорения или замедления потока на интегральные характеристики течения. Поэтому при достаточно больших числах Рейнольдса влиянием нестационарности на течение можно пренебречь.
-
Оптимизация кривой расхода
Из экспериментальных данных видно, что гидравлическое сопротивление при ускорении потока тем больше, чем больше критерий гидродинамической нестационарности. Отсюда вытекает задача о нахождении оптимальной кривой изменения расхода с G1 до G2 за время τ0. Решить такую задачу можно, минимизировав среднеквадратичное значение критерия гидродинамической нестационарности Kg*:
 (3)
(3)
Эта задача представляет собой классическую задачу минимизации функционала. После её решения и подстановки соответствующих граничных условий можно получить следующее выражение для кривой расхода:
 (4)
(4)
Исходя из условий Лежандра [10], найденная функция расхода отвечает минимуму среднеквадратичного значения критерия нестационарности. Таким образом, ускорение течения по данной кривой расхода является оптимальной с точки зрения гидравлических потерь.
Характерной особенностью этой кривой является тот факт, что критерий гидродинамической нестационарности во время ускорения/замедления течения остаётся постоянным:
 (5)
(5)
На Рис. 7-8 приведено сравнение полученной оптимизированной кривой расхода с синусоидальным законом увеличения расхода.

Рис. 7. Кривая расхода Gopt(τ) в сравнении с синусоидальным законом увеличения расхода G(τ)

Рис. 8. Критерий гидродинамической нестационарности в случаях кривой расхода Gopt(τ) в сравнении с критерием нестационарности в случае синусоидального закона увеличения расхода G(τ)
Далее мы рассмотрим вопросы моделирования переходных процессов при турбулентном течении в каналах в случае изменения во времени массового расхода.
-
Одномерное описание течения
При одномерном способе описании течения используют понятие среднерасходной скорости:
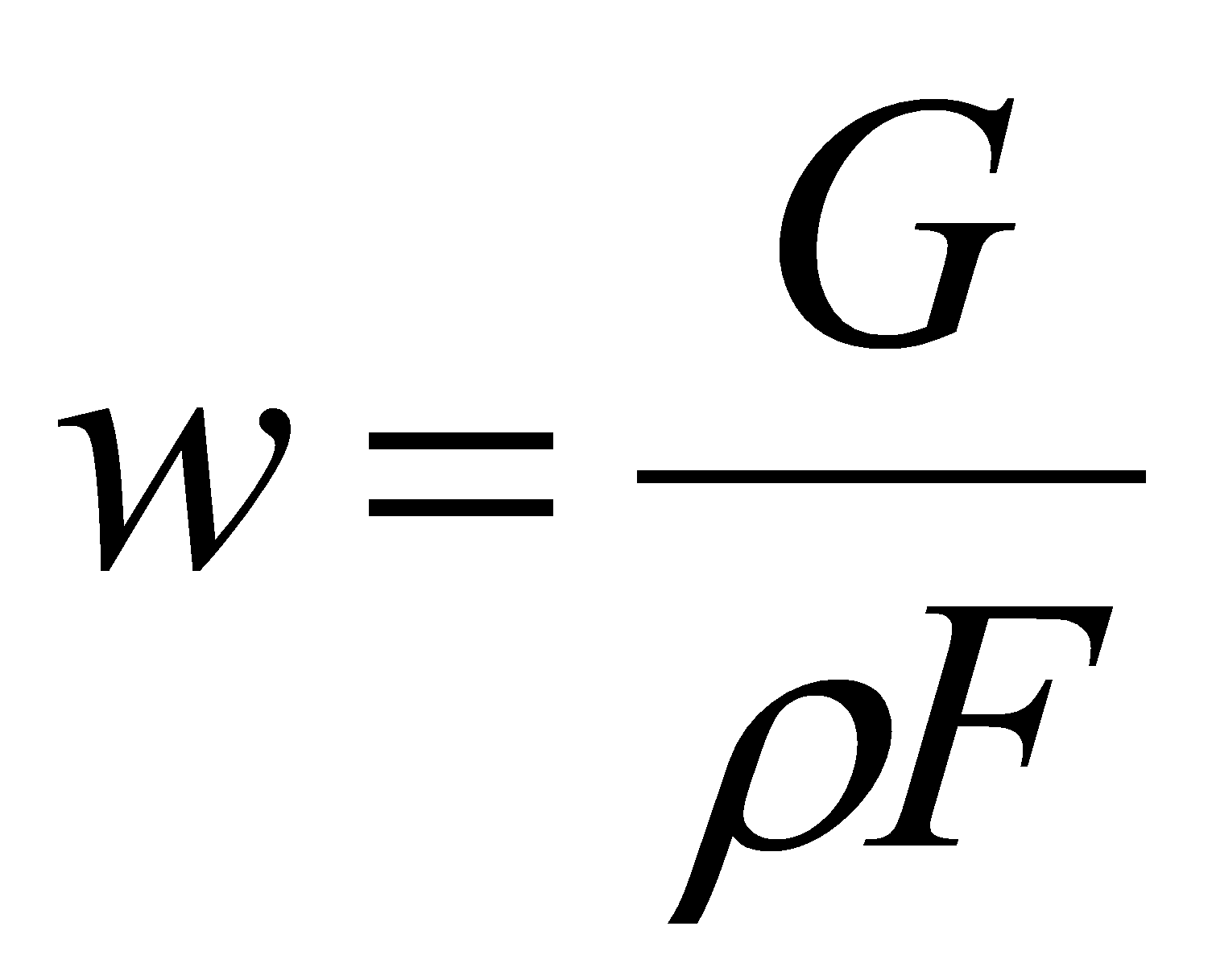 (6)
(6)
Тогда систему уравнений для неизотермического течения жидкости в канале можно записать следующим образом:
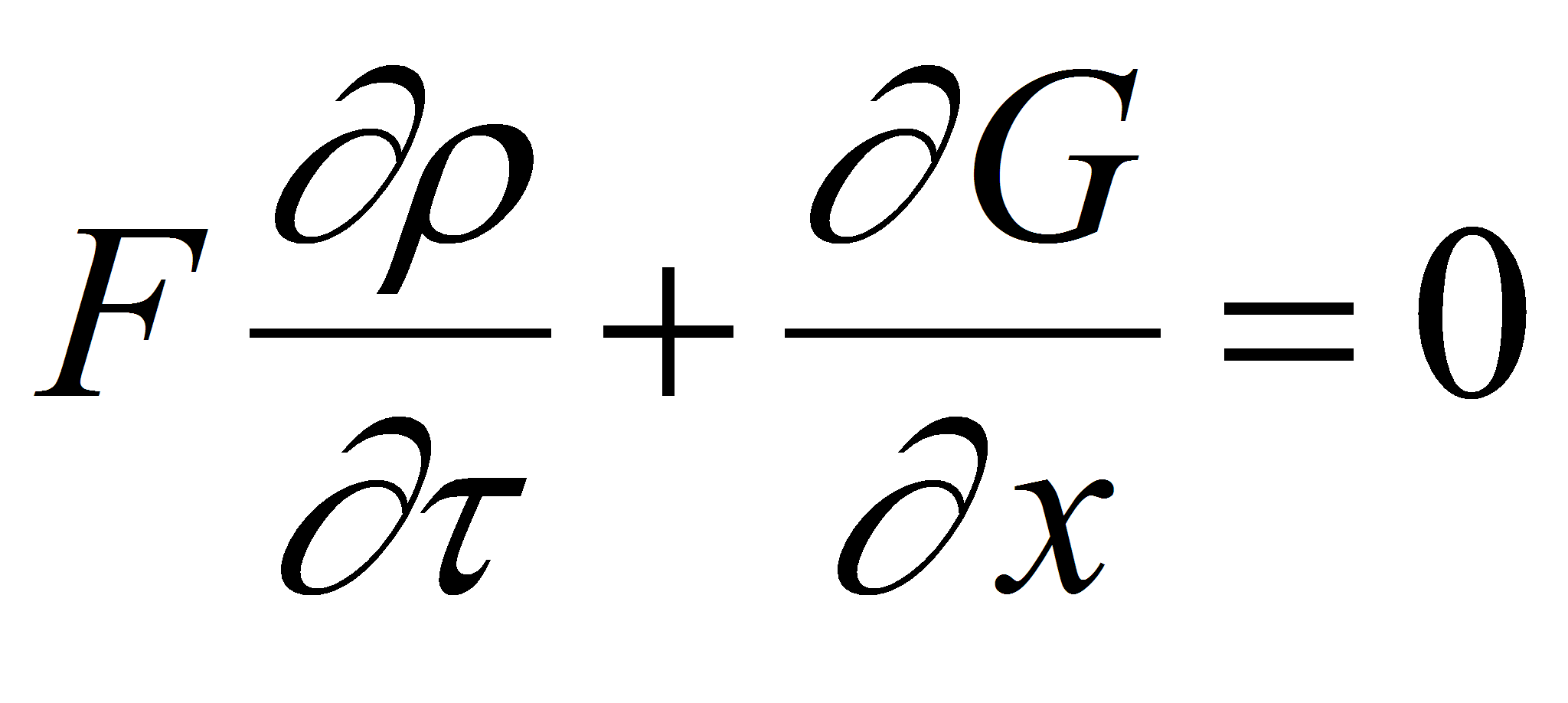 (7)
(7)
 (8)
(8)
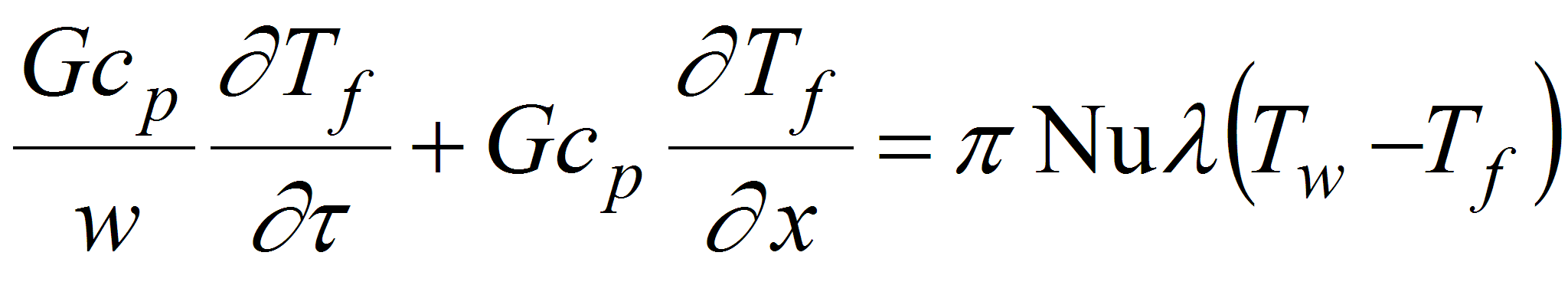 (9)
(9)
При этом ξ и Nu вычисляются по эмпирическим зависимостям (приведённым, например, в [3]).
Этот подход хорош своей простотой, однако полученные на сегодняшний день экспериментальные данные оказываются недостаточными для расчёта многих режимов течения. В частности для течений в условиях гидродинамической нестационарности пока что существует очень мало данных о степени влияния на течение температурного фактора (Tw/Tf).
Для предварительных расчётов, когда необходимо оценить лишь мощность на прокачку в нестационарном режиме при известной зависимости расхода от времени, можно воспользоваться следующей упрощённой формулой:
 (10)
(10)
Здесь 0 – коэффициент трения, рассчитанный по квазистационарной зависимости (например, по формуле Блаузиуса). Эта формула может быть легко получена из (8) в предположении стабилизации течения, отсутствия массовых сил и квазистационарном распределении давления по каналу. Вопросы, связанные с влиянием изменения расхода на турбулентную структуру в данном случае не рассматривается.
Зная зависимость для коэффициента трения, можно получить зависимость для числа Нуссельта, исходя из предположения, что турбулентное число Прандтля равно 1. Для круглых труб эта зависимость выглядит следующим образом [9]:
 (11)
(11)
Хотя предложенная методика является достаточно грубой, но она согласуется с опытом на качественном уровне (хотя и несколько по сравнению с опытом величины коэффициента трения и числа Нуссельта). При этом из формулы (10) отчётливо видно, что при больших числах Рейнольдса влияние нестационарности на гидравлическое сопротивление канала (а, следовательно, и на теплообмен) снижается (что было найдено авторами [3] опытным путём).
-
Аналитическое выражение для коэффициента трения
Известно, что в случае стационарного турбулентного течения в трубе, исходя из универсального профиля скорости, может быть получено следующее выражение для коэффициента трения [11,12]:
![]() (12)
(12)
Впервые это уравнение было получено Л. Прандтлем в 1932 г.
Видно, что в обычных функциях явно выразить нельзя, поэтому приходится использовать зависимости Блазиуса, Никурадзе и т.д., которые применимы только к своим достаточно узким диапазонам чисел Рейнольдса. При переходе из одного диапазона в другой может терпеть разрыв первого рода. Таким образом, при решении системы (7)-(9) или расчёта по (10) в случае перехода из одного диапазона чисел Рейнольдса в другой, функции скорости и температуры могут испытывать нефизичный скачок.
Избежать этого можно, если получить точное решение уравнения (12). Это можно сделать, используя предложенную в [13] функцию Ламберта W(x).
Данная функция является определяется как обратная функция к f(w) = wew, для комплексных w. Для любого комплексного z она определяется функциональным уравнением [13]:
![]() (13)
(13)
W-функция Ламберта нашла широкое применение в математической физике (см. например [14]).
Исходя из вышеизложенного, точное аналитическое выражение для (12) может быть записано в виде:
 (14)
(14)
-
Многомерное описание течения
По причинам, упомянутым выше, часто возникает необходимость в расчёте с использованием многомерного подхода. При этом решается система уравнений Навье-Стокса.
Как известно, если поток турбулентный, решить эти уравнения напрямую достаточно сложно и это требует больших вычислительных мощностей (хотя этот подход последнее время применяется всё чаще). Самым распространённым методом решения является применение осреднения по Рейнольдсу (в случае несжимаемого течения) или по Фавру (сжимаемое течение) [4, 5]. При этом для замыкания системы требуются дополнительные уравнения, так называемая модель турбулентности.
Авторами [6] применялась для расчётов модифицированная двухпараметрическая модель k-ε. В работе [7] автор использовал для анализа турбулентного течения в трубе как двухпараметрическую модель, так и уравнения для вторых моментов флуктуаций скорости.
Результаты, приведенные в [6, 7] прямо противоположны результатам экспериментальных исследований. Согласно им, увеличение во времени расхода газа ведёт к снижению по сравнению с квазистационарными коэффициента трения и теплоотдачи и наоборот. Скорее всего, причиной этого является рассмотрение в данных работах лишь стабилизированного участка течения со стандартным профилем скорости по Карману в качестве граничного условия на входе. Автор [7] предположил возможность локальной деформации профиля скорости вблизи стенки вследствие конструктивных особенностей впускного устройства, обеспечивающего изменение расхода во времени. В свете этой гипотезы он продемонстрировал, что теории, представленные в [6, 7] могут приводить к результатам, сходным с результатами опытов.
Подход, использованный в [6, 7], когда течение полагается полностью стабилизированным, а в качестве граничного условия используется квазистационарный турбулетный профиль скорости, представляется не совсем корректным, как было показано в [1], профиль скорости при ускорении и замедлении потока существенно отличается от квазистационарного. При этом указанное в [7] возмущение профиля, названное там «искусственным», на самом деле оказывается вполне естественным. Профиль скорости деформируется ещё на начальном участке течения.
Расчёты, выполненные в МАИ, проводились с учётом начального участка. При расчётах использовалась система уравнений Рейнольдса:
 (15)
(15)
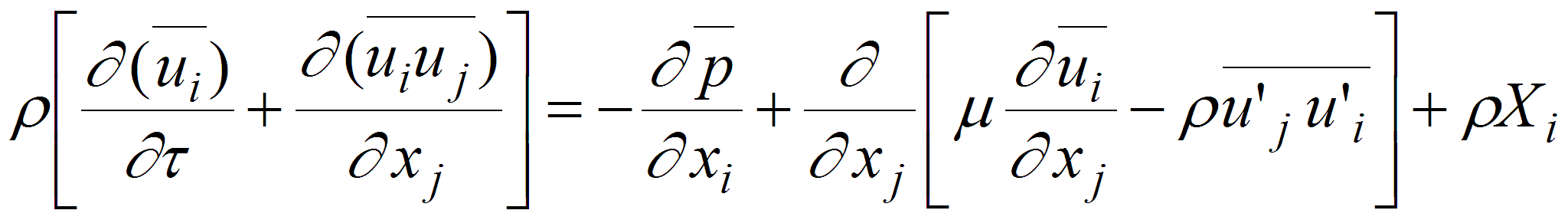 (16)
(16)
 (17)
(17)
Геометрия канала в расчётах соответствовала геометрии реальной, применявшейся в экспериментах [3] трубы (диаметр 42.8 мм, длина – 3 м). На входе в канал в качестве граничного условия был установлен расход как функция от времени, на выходе – атмосферное давление. В качестве моделей турбулентности использовались стандартная k-ε модель и двухслойная модель Ментера [8]. Задача решалась в двумерной постановке. Дискретизация уравнений (15)-(17) производилась на основе метода конечных объёмов. Использовалась сетка с ячейками прямоугольной формы 200x3000, сетка сгущалась по направлению к стенке таким образом, что безразмерное расстояние от стенки y+ пристеночного узла было меньше 1.
Применение модели k-ε не привело к удовлетворительным результатам – была получена квазистационарная картина. Возможно дело в том, что стандартная k-ε модель является моделью высокорейнольдсовского типа. Применение же модели Ментера позволило получить результаты, сходные с результатами экспериментов (см. Рис. 9). Также в ходе расчетов было замечено некоторое увеличение длины начального участка течения. При расчётах неизотермического течения тепловой стабилизации потока в рассчитываемом канале не происходило вовсе (см. Рис. 10).

Рис. 9. Сравнение результатов расчёта с использованием модели Ментера влияния ускорения потока на коэффициент трения с экспериментальными данными [3]. Режимные параметры: Re=3100…9300, Tw/Tf=1, Kg*max =0.088.

Рис. 10. Рассчитанное распределение приведенной температуры по оси канала при ![]() Re=3100…9300, Kg*max =0.088.
Re=3100…9300, Kg*max =0.088.
При расчёте неизотермического течения данные по теплоотдаче не сходились с экспериментами [3] – в результате расчётов зависимость по теплоотдаче получалась сходная с квазистационарной (коэффициент теплоотдачи рассчитывался по градиенту температуры на стенке). Этому было найдено следующее объяснение: в экспериментах [3] авторы производили измерения только в одном сечении трубы (на расстоянии 2.5 метра от входа), в котором, как они считали, течение стабилизировано. Число Нуссельта рассчитывалось ими с помощью интеграла Лайона (который предполагает стабилизацию течения):
 (18)
(18)
Данные расчётов показывают, что тепловой стабилизации в указанном сечении не происходит. Однако, если подставить рассчитанный профиль скорости в формулу (18), то число Нуссельта с точностью до 20% совпадает с данными [3]. Таким образом, повышение рассчитанного коэффициента теплоотдачи могло быть вызвано аксиальными тепловым потоком.
Работа выполнена при содействии Гранта президента РФ по поддержке молодых докторов наук (МД-2246) и Гранта Российского фонда фундаментальных исследований (08-08-00226-а).
Список литературы
-
Калинин Э.К. Методы расчёта сопряженных задач теплообмена / Э.К. Калинин, Г.А. Дрейцер, В.В. Костюк, И.И. Берлин. М: Машиностроение, 1983. 232 с.
-
Марков С. Б. Экспериментальное исследование скоростной структуры и гидравлических сопротивлений в неустановившихся напорных турбулентных потоках // Механика жидкости и газа. 1973. ╧2. С. 65-75
-
Дрейцер Г.А., Краев В.М. Турбулентные течения газа при гидродинамической нестационарности– Красноярск: САА, 2001.- 148 с.
-
Волков К.Н., Емельянов В.Н. Моделирование крупных вихрей в расчётах турбулентных течений. – М.: ФИЗМАТЛИТ, 2008. – 368 с.
-
И.А. Белов, С.А. Исаев. Моделирование турбулентных течений: Учебное пособие, Балт. гос. техн. ун-т. СПб., 2001. 108 с.
-
Валуева Е.П., Чэнь Лэй . Численное моделирование процессов теплообмена и гидродинамики при нестационарном турбулентном течении в трубе жидкости с переменными свойствами // Вестник МЭИ. 2000. ╧ 6. С. 38
-
Деревич И.В. О моделировании нестационарной гидродинамики при турбулентном течении в трубах // ТВТ, 2005, т. 43, ╧2, сс. 231-248.
-
Menter F.R., 1993 Zonal two equation k-ω turbulence models for aerodynamic flows, AIAA Paper, N93-2906, 21p.
-
Л.Г. Лойцянский. Механика жидкости и газа. Изд. 5-е, переработанное, Главная редакция физико-математической литературы издательства «Наука», М., 1978, 736 стр
-
А.Д. Мышкис. Прикладная математика для инженеров. Специальные курсы. М: ФИЗМАТЛИТ, 2007 – 688 с.
-
Кутателадзе С.С. Основы теории теплообмена. — Изд. 5-е перераб. и доп. — М: Атомиздат, 1979, 416 с.
-
Дрейцер Г.А. Основы конвективного теплообмена в каналах: Учебное пособие. – М.: Изд-во МАИ, 1989. – 84 с.
-
Corless R.M., Gonnet G.H., Hare D.E., Jeffrey D.J., Knuth D.E. On the Lambert W function. // Advances Computational Maths. 1996. Vol. 5, p. 329–359.
-
Дубинов А.Е., Дубинов И.Д., Сайков С.К. W-функция Ламберта и её применение в математических задачах физики: Учеб. пособие для вузов. – Саров: ФГУП «РФЯЦ-ВНИИЭФ», 2006, 160 с.
Публикации с ключевыми словами: гидродинамика
Публикации со словами: гидродинамика
Смотри также:
- Структурные характеристики двухфазных газожидкостных потоков в условиях действия периодических поперечных сил
- Влияние внешних гидродинамических параметров высокоскоростных подводных аппаратов на их тактико-технические характеристики
- Исследование гидродинамических источников колебаний в двухзавитковом спиральном отводе центробежного насоса НМ1250
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



