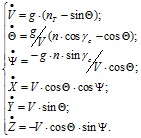научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 08, август 2009
УДК 519.6
МГТУ им. Н.Э. Баумана
Для летальных аппаратов (ЛА) разных классов актуальной является задача обеспечения их траекторной безопасности. Для решения этой задачи необходимо построение области достижимости ЛА в реальном времени, что, очевидно, может быть выполнено с помощью многократного интегрирования соответствующей системы обыкновенных дифференциальных уравнений. Однако такой подход требует неприемлемо больших вычислительных ресурсов. Целью работы является исследование возможности применения нейронных сетей для построения области достижимости ЛА. Работа является продолжением работы [1], в которой более детально приведены постановка задачи, а также описания используемых нейронных сетей.
1. Постановка задачи
Уравнения движения центра масс ЛА в нормальной земной системе координат ![]() описываются следующей системой нелинейных дифференциальных уравнений [2]:
описываются следующей системой нелинейных дифференциальных уравнений [2]:
|
|
(1)
|
,
где ![]() – скорость ЛА,
– скорость ЛА, ![]() – угол наклона траектории,
– угол наклона траектории, ![]() – угол поворота траектории,
– угол поворота траектории, ![]() – высота ЛА,
– высота ЛА, ![]() – тангенциальная перегрузка,
– тангенциальная перегрузка, ![]() – нормальная перегрузка,
– нормальная перегрузка, ![]() – скоростной угол крена,
– скоростной угол крена, ![]() – ускорение свободного падения.
– ускорение свободного падения.
Вектор управления ЛА задается вектором
![]()
Область достижимости ЛА определяется как множество значений вектора координат его центра масс в момент времени ![]() полученных при заданном начальном состоянии ЛА и всех возможных допустимых управлениях. Очевидно, что динамика области достижимости может быть описана динамикой ее границ.
полученных при заданном начальном состоянии ЛА и всех возможных допустимых управлениях. Очевидно, что динамика области достижимости может быть описана динамикой ее границ.
В работе [2] были получены структуры управлений, приводящих на границы области достижимости при фиксированным угле крена. Структура управления, приводящего на дальнюю границу области достижимости, имеет вид (рис. 1):
|
|
(2)
|
где ![]() – время перехода на особый участок управления
– время перехода на особый участок управления ![]() ,
, ![]() - длительность полета,
- длительность полета, ![]()
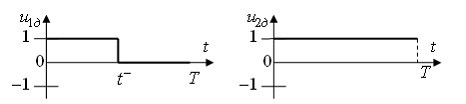
Рисунок 1 – Структура оптимальных управлений, приводящих на дальнюю границу области достижимости
2. Структура нейронных сетей
В работе рассматривается три нейронных сети [1].
Нейронная сеть 1 (НС1) определяет координаты границы области достижимости ЛА при задании граничного управления. Входной слой сети состоит из элементов ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() где
где ![]() – момент времени переключения нормальной перегрузки
– момент времени переключения нормальной перегрузки ![]() со значения
со значения ![]() до
до ![]() ,
, ![]() – угол крена ЛА. Сеть содержит два скрытых слоя, содержащих одинаковое количество персептронов с функцией активации – гиперболический тангенс. Выходной слой сети состоит из трех нейронов с линейной функцией активации, соответствующих координатам
– угол крена ЛА. Сеть содержит два скрытых слоя, содержащих одинаковое количество персептронов с функцией активации – гиперболический тангенс. Выходной слой сети состоит из трех нейронов с линейной функцией активации, соответствующих координатам ![]() и
и ![]() конечного положения ЛА (рисунок 2).
конечного положения ЛА (рисунок 2).

Рисунок 2 – Входы – выходы нейронной сети НС1
Нейронная сеть типа НС1, фактически, заменяет интегрирование системы обыкновенных дифференциальных уравнений, описывающих движение центра масс ЛА с граничными управлениями.
Нейронная сеть 2 (НС2) определяет расстояние до границы области достижимости в заданном направлении. Входной слой сети состоит из элементов ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() где
где ![]() ,
, ![]() – углы, которые определяют требуемое направление в пространстве. Выходом сети является длина радиус-вектора конечного положения ЛА на дальней границе области достижимости (рисунок 3).
– углы, которые определяют требуемое направление в пространстве. Выходом сети является длина радиус-вектора конечного положения ЛА на дальней границе области достижимости (рисунок 3).

Рисунок 3 – Входы – выходы нейронной сети НС2
Нейронная сеть 3 (НС3) определяет управление, приводящее ЛА на границу области достижимости в заданном направлении. Входной слой сети состоит из элементов ![]() ,
, ![]() ,
, ![]()
![]() , где
, где ![]() ,
, ![]() – углы, которые определяют требуемое направление в пространстве. Выходом сети являются параметры управления
– углы, которые определяют требуемое направление в пространстве. Выходом сети являются параметры управления![]() и
и ![]() где
где ![]() – момент времени переключения нормальной перегрузки
– момент времени переключения нормальной перегрузки ![]() со значения
со значения ![]() до значения
до значения ![]() ,
, ![]() – заданный угол крена ЛА (рисунок 4).
– заданный угол крена ЛА (рисунок 4).

Рисунок 4 – Входы – выходы нейронной сети НС3
3. Схема исследования
Рассматривается задача (5), в которой входные величины варьируются в следующих пределах:
![]() ,
,
![]() ,
,
![]() .
.
Здесь ![]() – скорость звука в воздухе.
– скорость звука в воздухе.
Обучающая выборка состоит из 4500 элементов. Из нее случайным образом выбирается 20% проверочных точек для определения момента окончания обучения. Начальные веса и пороговые элементы нейронов каждого слоя устанавливаются в соответствии с алгоритмом инициализации Нгуен-Видроу (Nguyen-Widrow) [3]. Данный алгоритм выбирает такие их значения, чтобы область выходных значений каждого нейрона в слое была приблизительно равномерно распределена по области входных значений слоя. При генерации этих значений используются случайные числа.
Обучение каждой из сетей выполняется в среднем 10 раз с различными начальными весами и пороговыми значениями; затем выбирается сеть с минимальным значением ошибки. Исследование точности аппроксимации обученной сети выполнено с использованием тестовой выборки, содержащей более 20000 элементов. Точность аппроксимации оценивается следующими величинами.
Средняя относительная погрешность
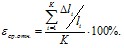
Здесь ![]() – мощность тестового множества,
– мощность тестового множества, ![]() – расстояние от тестовой точки до точки, полученной на выходе нейронной сети,
– расстояние от тестовой точки до точки, полученной на выходе нейронной сети, ![]() – расстояние от начальной точки
– расстояние от начальной точки ![]() до тестовой точки.
до тестовой точки.
Средняя абсолютная погрешность

Максимальная относительная погрешность

Максимальная абсолютная погрешность
![]()
Среднее квадратичное отклонение

Обучение и тестирование нейронных сетей выполнено в среде Matlab [4].
Исследуемые сети содержат два скрытых слоя, состоящих из одинакового количества персептронов с функцией активации – гиперболический тангенс. Выходной слой сети состоит из нейронов с линейной функцией активации. Для обучения используется метод Левенберга-Маркара (Levenberg-Marquardt Algorithm) [5].
4. Результаты исследования
В таблице 1 приведены результаты исследования точности аппроксимации дальней границы области достижимости сетями НС1 с различным количеством нейронов. Эта таблица и иллюстрирующая ее гистограмма, изображенная на рисунке 5, показывают, что с увеличением числа нейронов в сети погрешность аппроксимации стабильно уменьшается. Среднее и максимальное значение погрешности у сети из 22 нейронов равны 1.38% и 11.6%, а для сети из 40 нейронов - 0.55% и 3.12% соответственно.
Таблица 1 – Сравнение сетей НС1 с различным количеством нейронов
|
Количество нейронов
|
Средняя относительная погрешность
|
Средняя абсолютная погрешность, м
|
Среднее квадратичное отклонение
|
Максимальная
относительная погрешность
|
Максимальная
абсолютная погрешность, м
|
|
22
|
1.38 %
|
79.69
|
52.15
|
11.64 %
|
707.4
|
|
24
|
1.31 %
|
75.71
|
48.38
|
10.57 %
|
694.6
|
|
26
|
1.06 %
|
61.21
|
42.92
|
9.76 %
|
651.1
|
|
28
|
0.89 %
|
51.80
|
35.72
|
9.31 %
|
620.9
|
|
30
|
0.84 %
|
48.75
|
33.88
|
9.15 %
|
609.6
|
|
32
|
0.82 %
|
46.97
|
32.33
|
9.29 %
|
578.9
|
|
34
|
0.71 %
|
40.90
|
31.83
|
6.37 %
|
424.9
|
|
36
|
0.65 %
|
37.51
|
27.83
|
5.14 %
|
401.3
|
|
38
|
0.59 %
|
33.58
|
25.34
|
5.13 %
|
382.3
|
|
40
|
0.55 %
|
31.74
|
23.18
|
3.12 %
|
355.8
|

Рисунок 5 – Средняя погрешность аппроксимации дальней границы сетями НС1 с различным количеством нейронов
Пример аппроксимации дальней границы области достижимости, полученной с помощью сети НС1, приведен на рисунке 6.

Рисунок 6 – Аппроксимация дальней границы области достижимости, построенной при начальных условиях ![]()
![]() ,
, ![]() (использована нейронная сеть НС1, состоящей из 32 нейронов)
(использована нейронная сеть НС1, состоящей из 32 нейронов)
В таблице 2 приведены результаты исследования точности аппроксимации области достижимости сетями НС2 с различным количеством нейронов. Таблица 2 и гистограмма, изображенная на рисунке 7, показывают, что сеть НС2 аппроксимирует границу области достижимости более точно по сравнению с сетью НС1.
Таблица 2 – Сравнение сетей НС2 с различным количеством нейронов
|
Количество нейронов
|
Средняя относительная погрешность
|
Средняя абсолютная погрешность, м
|
Среднее квадратичное отклонение
|
Максимальная
относительная погрешность
|
Максимальная
абсолютная погрешность, м
|
|
22
|
0.25 %
|
14.43
|
12.70
|
3.75 %
|
302.1
|
|
24
|
0.21 %
|
12.08
|
10.51
|
3.36 %
|
294.6
|
|
26
|
0.18 %
|
10.31
|
9.18
|
2.86 %
|
252.8
|
|
28
|
0.17 %
|
9.26
|
8.15
|
2.52 %
|
240.4
|
|
30
|
0.15 %
|
8.60
|
7.65
|
2.48 %
|
220.7
|
|
32
|
0.15 %
|
8.52
|
7.41
|
2.11 %
|
219.4
|
|
34
|
0.14 %
|
7.97
|
6.89
|
2.24 %
|
195.9
|
|
36
|
0.12 %
|
6.92
|
6.09
|
1.80 %
|
173.6
|
|
38
|
0.11 %
|
6.35
|
5.63
|
1.69 %
|
167.4
|
|
40
|
0.09 %
|
5.20
|
4.64
|
1.53 %
|
152.4
|
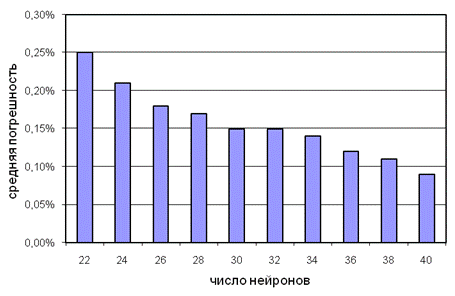
Рисунок 7 – Средняя погрешность аппроксимации дальней границы сетями НС2 с различным количеством нейронов
В таблице 3 приведены результаты исследования точности аппроксимации области достижимости сетями НС3 с различным количеством нейронов. Таблицу 3 иллюстрирует рисунок 8.
Таблица 3 – Сравнение сетей НС3 с различным количеством нейронов
|
Количество нейронов
|
Средняя относительная погрешность
|
Средняя абсолютная погрешность, м
|
Среднее квадратичное отклонение
|
Максимальная
относительная погрешность
|
Максимальная
абсолютная погрешность, м
|
|
22
|
0.83 %
|
47.03
|
52.73
|
8.21 %
|
593.2
|
|
24
|
0.77 %
|
43.85
|
48.24
|
7.31 %
|
463.0
|
|
26
|
0.63 %
|
35.77
|
38.35
|
6.96 %
|
415.5
|
|
28
|
0.53 %
|
30.58
|
33.64
|
5.94 %
|
401.4
|
|
30
|
0.50 %
|
28.56
|
31.42
|
5.47 %
|
395.1
|
|
32
|
0.49 %
|
27.98
|
30.78
|
5.41 %
|
350.0
|
|
34
|
0.43 %
|
24.52
|
26.97
|
4.29 %
|
346.9
|
|
36
|
0.41 %
|
22.21
|
25.44
|
4.80 %
|
322.2
|
|
38
|
0.35 %
|
20.19
|
22.21
|
3.12 %
|
280.2
|
|
40
|
0.34 %
|
18.46
|
20.71
|
3.06 %
|
275.4
|

Рисунок 8 – Средняя погрешность аппроксимации дальней границы области достижимости сетями НС3 с различным количеством нейронов
Из таблиц 1 – 3 можно сделать вывод, что сети НС3 аппроксимируют границу области достижимости лучше сетей НС1, но хуже сетей НС2.
В таблице 4 приведены результаты исследования точности аппроксимации последовательно соединенных сетей НС3 и НС1 (рисунок 9). Подобное объединение сетей позволяет осуществлять проверку допустимости входных данных - точка с координатами ![]() ,
, ![]() ,
, ![]() должна лежать вблизи прямой, задаваемой углами (α, β). На вход сети НС3 в этом случае поступают углы (α, β), задающие направление, вдоль которого должна быть найдена точка границы области достижимости. Выход нейронной сети НС3 аппроксимирует управление, приводящее в эту точку. Результат работы сети НС3 подается на вход сети НС1, которая уже аппроксимирует координаты точек на границе области достижимости. Количество нейронов в обеих сетях одинаково.
должна лежать вблизи прямой, задаваемой углами (α, β). На вход сети НС3 в этом случае поступают углы (α, β), задающие направление, вдоль которого должна быть найдена точка границы области достижимости. Выход нейронной сети НС3 аппроксимирует управление, приводящее в эту точку. Результат работы сети НС3 подается на вход сети НС1, которая уже аппроксимирует координаты точек на границе области достижимости. Количество нейронов в обеих сетях одинаково.

Рисунок 9 – Последовательно соединенные сети НС3 и НС1
Таблица 4 – Сравнение точности аппроксимации сетей НС1, НС3 с различным количеством нейронов
|
Количество нейронов
|
Средняя относительная погрешность
|
Средняя абсолютная погрешность, м
|
Среднее квадратичное отклонение
|
Максимальная относительная погрешность
|
Максимальная абсолютная погрешность, м
|
|
22
|
1.79 %
|
103.29
|
83.67
|
15.75 %
|
839.1
|
|
24
|
1.68 %
|
95.76
|
76.15
|
14.21 %
|
712.3
|
|
26
|
1.38 %
|
78.66
|
62.14
|
13.26 %
|
715.4
|
|
28
|
1.16 %
|
67.28
|
53.82
|
12.28 %
|
640.1
|
|
30
|
1.08 %
|
61.56
|
49.56
|
12.41 %
|
620.4
|
|
32
|
1.07 %
|
60.99
|
47.40
|
11.99 %
|
553.0
|
|
34
|
0.93 %
|
53.47
|
42.78
|
8.52 %
|
556.2
|
|
36
|
0.89 %
|
50.73
|
40.74
|
8.54 %
|
563.2
|
|
38
|
0.75 %
|
42.97
|
32.23
|
6.69 %
|
426.1
|
|
40
|
0.72 %
|
41.04
|
30.37
|
5.13 %
|
405.3
|
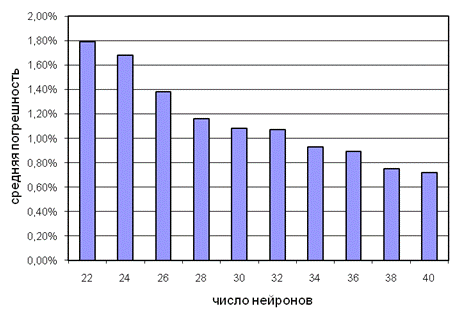
Рисунок 10 – Средняя погрешность аппроксимации дальней границы области достижимости сетями НС3, НС1 с различным количеством нейронов
Таблица 4 и соответствующая гистограмма, изображенная на рисунке 10, показывают, что результаты аппроксимации последовательно соединенными сетями НС3, НС1 несколько хуже, чем сетями НС1 (таблица 1). Например, при 22 нейронах значения средней погрешности равны 1.79% и 1.38%, а максимальной погрешности – 15.75% и 11.64% соответственно. Однако то, что указанные величины сравнимы, говорит о хорошей устойчивости сетей к погрешностям входных данных и позволяет сделать вывод о возможности их совместного использования.
Заключение
Для определения границы области достижимости требуется построить три сети типа НС1, аппроксимирующие ближнюю, дальнюю и боковую границы. Количество нейронов в сетях необходимо определить экспериментально, исходя из требований к точности аппроксимации. Данный тип сетей фактически заменяет интегрирование системы уравнений, описывающих движение центра масс ЛА с граничными управлениями.
В работе также предложено для каждой границы области достижимости строить дополнительно нейронные сети НС2, НС3, определяющие положение ЛА по заданному направлению и граничное управление, приводящее в соответствующую точку области достижимости.
Проведенное исследование подтвердило возможность применения нейронных сетей НС1 – НС3 для задачи аппроксимации трехмерной области достижимости ЛА. В ходе дальнейших работ планируется реализация и исследование эффективности других методов быстрого построения области достижимости.
Литература
- Козлова О.Г. Нейросетевая аппроксимация границы области достижимости летательного аппарата. 1. Двумерный случай // Наука и образование: электронное научно- техническое издание, www.technomag.edu.ru, июль, 2009.
- Воронов Е.М., Карпунин А.А. Алгоритм оценки границ области достижимости летательного аппарата с учетом тяги // Вестник МГТУ им. Н.Э.Баумана, Сер. «Приборостроение», ╧4 (69), 2007, С.81–99.
- Медведев, Потемкин В. Нейронные сети. Matlab 6. – М.: Диалог МИФИ, 2001. – 496 с.
- Медведев, Потемкин В. Нейронные сети. Matlab 6. – М.: Диалог МИФИ, 2001. – 507 с.
- Справочная информация для программного комплекса Matlab 7.7.0 (R2008b).
- Саймон Хайкин Нейронные сети: полный курс. 2-е издание. - М: "Вильямс", 2006 г. – 282 с.
Публикации с ключевыми словами: нейросетевая аппроксимация, область достижимости динамической системы
Публикации со словами: нейросетевая аппроксимация, область достижимости динамической системы
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||