научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 07, июль 2009
Скорнякова А., Суханова Д., Шарыпова С.
средняя школа ╧ 651, 9 класс
Научный руководитель:
Аксенова Елена Владимировна
учитель информатики средней школы ‡‚ 651
После изучения систем счисления на уроках информатики захотелось найти как можно больше информации о древних непозиционных системах счисления. Это так интересно увидеть и понять, как в древности люди писали цифры, какие для этого они применяли значки. Как из этих цифр они составляли числа. Особенно интересным для нас было выяснить, применяются ли древние системы счисления в современной жизни и как? Таким образом, сформировались цели и задачи нашей проектной работы.
Цель проекта: Изучение древних непозиционных систем счисления и выявление применения их в современных сферах деятельности человека.
Основные задачи:
1. Поиск информации о непозиционных системах счисления, как в библиотеке, так и в Интернете.
2. Изучение каждой системы счисления – правил составления чисел в них.
3. Исследование основных сфер деятельности современного человека (науки, образования, архитектуры, дизайна, и т. д.) и выявление связей с древними системами счисления.
4. Разработка дидактического материала для уроков информатики по непозиционным системам счисления.
Много интересного о разных системах нумерации на сайте «Всевозможные нумерации и системы счисления» и в книге «Три дня в Карликании» [1]. Подробно о древних цифрах и числах можно найти в книгах [3-5]. История нуля рассказана в статье «Триединый нуль» [6].
1. Цифры и системы счисления
«Все есть число», – говорили пифагорийцы (ученики древнегреческого математика Пифагора). Значит все можно обозначить числом. Так как многие предметы внешнего мира имеет схожую форму, возникла потребность их сосчитать. Например, сколько коров в стаде. Сколько добыто рыб, или зайцев. Т.е. число и арифметика возникли из практической деятельности человека. Так как многие народы в древности не общались друг другом, то у разных народов возникли разные системы счисления и представления чисел и цифр.
Число – это обобщение, так как разными числами можно подсчитать разные предметы.
Цифры – это значки, с помощью которых записывают числа. Система счисления или нумерация – это способ записи чисел с помощью цифр.
1.2. Позиционные и непозиционные системы счисления
Системы счисления бывают непозиционными (аддитивными) и позиционными (мультипликативными). Чтобы разобраться в этом рассмотрим для примера нашу «арабскую» систему счисления. Например, число 3333 – три тысячи триста тридцать три. Здесь каждая цифра «3» в зависимости от того, в каком месте находиться обозначает свое число.
Первая тройка слева, это три тысячи, вторая, три сотни, третья – три десятка, четвертая – три единицы. Т.е. это позиционная система. В таких же системах значение каждой цифры, зависит от ее положения (места, позиции) в записи числа. В непозиционных системах значение каждой цифры не зависит от ее положения (места, позиции) в записи числа. Число 3333 можно представить в таком виде 3×1000 + 3×100 + 3×10 + 3. Т.е. для представления этого числа используется умножение (по-английски multiplication), отсюда название этой системы – мультипликативная.
В непозиционных же системах для представления числа используется сложение всех цифр, по-английски сложение – add. Поэтому другое название этих систем – аддитивные.
1.3. Основание системы счисления
 Основание системы счисления – это число, на основе которого ведется счет. Например, если основание системы счисления равно десяти, то минимальная счетная группа этой системы счисления равна десяти, это значит, что, сосчитав какие-либо предметы до десяти, мы считаем снова с единицы, но при этом запоминаем число десятков. В нашей «арабской» системе основанием является число десять. Есть системы счисления и с другим основанием. Это такие системы счисления как пятеричная, двенадцатеричная, двадцатеричная, шестидесятеричная.
Основание системы счисления – это число, на основе которого ведется счет. Например, если основание системы счисления равно десяти, то минимальная счетная группа этой системы счисления равна десяти, это значит, что, сосчитав какие-либо предметы до десяти, мы считаем снова с единицы, но при этом запоминаем число десятков. В нашей «арабской» системе основанием является число десять. Есть системы счисления и с другим основанием. Это такие системы счисления как пятеричная, двенадцатеричная, двадцатеричная, шестидесятеричная.
 Десятеричная и пятеричная система возникла от того факта, что на одной руке человека пять пальцев, на обеих руках 10 пальцев.
Десятеричная и пятеричная система возникла от того факта, что на одной руке человека пять пальцев, на обеих руках 10 пальцев.
Так проще считать. Если добавить пальцы и на ногах, то будет понятная и двадцатеричная система. Происхождение двенадцатеричной системы тоже связано со счетом на пальцах. Считали большой палец руки и фаланги остальных четырех пальцев.
Если двенадцать умножить на пять, получим шестидесятеричную систему. Например, на одной руке загибаем пальцы, пока не получим, что отсчитано, пять штук, а на другой руке прикосновением большого пальца к суставам остальных четырех указываем количество этих пятерок.
В некоторых системах счисления используются для обозначения цифр буквы, такие системы счисления называются алфавитными.
Итак, бывают непозиционные (аддитивные) и позиционные (мультипликативные), пятеричные, десятичные, двенадцатеричные, двадцатеричные, шестидесятеричные и алфавитные системы счисления.
Вначале рассмотрим непозиционные (аддитивные) системы счисления.
2. Непозиционные системы счисления
2.1. Простая система счисления
 У первобытных людей не было даже чисел, они количество предметов отображали равным количеством каких-либо значков. Такими значками могли быть зарубки, черточки, точки, а так же узелки на веревках.
У первобытных людей не было даже чисел, они количество предметов отображали равным количеством каких-либо значков. Такими значками могли быть зарубки, черточки, точки, а так же узелки на веревках.
|
1 |
½ |
|
2 |
½½ |
|
3 |
½½½ |
|
4 |
½½½ |
|
5 |
½ ½ ½ ½ ½ и т. д. |
Это самая простая система счисления. В этой системе счисления для записи чисел используется только одна цифра. Ее можно изобразить в виде палочки ½, кружочка │›, или любой другой фигуры. Тогда числа будут записываться примерно так:
Такая система счисления использовалась, и до сих пор используется народами, не имеющими письменности.
Но иногда такой системой счисления пользуются и современные люди, например, отмечая зарубками количество прошедших дней, или карандашом отмечая черточками в тетради количество проданных товаров. И уж совсем не обойтись без такой системы счисления при обучении счету маленьких детей.


Позже, для облегчения счета, эти значки стали группировать по три или по пять. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу.
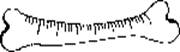 Но это удобно, пока числа небольшие. Вы только представьте себе число 1 000 записанное с помощью кучки камушков, а 1 000 000? Неудобно?
Но это удобно, пока числа небольшие. Вы только представьте себе число 1 000 записанное с помощью кучки камушков, а 1 000 000? Неудобно?
И люди начали изобретать системы счисления.
 2.2. Древнеегипетская десятичная
2.2. Древнеегипетская десятичная
Примерно в третьем тысячелетии до нашей эры древние египтяне придумали свою числовую систему, в которой для обозначения ключевых чисел 1, 10, 100 и т.д. использовались специальные значки – иероглифы.
Все остальные числа составлялись из этих ключевых при помощи операции сложения. Система счисления Древнего Египта является десятичной, но непозиционной и аддитивной.
|
|
1. Как и большинство людей для счета небольшого количества предметов Египтяне использовали палочки. |
|
|
Если палочек нужно изобразить несколько, то их изображали в два ряда, причем в нижнем ряду должно быть столько же палочек, сколько и в верхнем, или на одну больше. |
|
|
10. Такими путами египтяне связывали коров |
|
|
Если нужно изобразить несколько десятков, то иероглиф повторяли нужное количество раз. Тоже самое относится и к остальным иероглифам. |
|
|
100. Это мерная веревка, которой измеряли земельные участки после разлива Нила. |
|
|
1 000. Вы когда-нибудь видели цветущий лотос? Если нет, то вам никогда не понять, почему Египтяне присвоили такое значение изображению этого цветка. |
|
|
10 000. «В больших числах будь внимателен!» – говорит поднятый вверх указательный палец. |
|
|
100 000. Это головастик. Обычный лягушачий головастик. |
|
|
1 000 000. Увидев такое число, обычный человек очень удивится и возденет руки к небу. Это и изображает этот иероглиф |
|
|
10 000 000. Египтяне поклонялись Амону Ра, богу Солнца, и, наверное, поэтому самое большое свое число они изобразили в виде восходящего солнца |
Записывались цифры числа начиная с больших значений и заканчивая меньшими. Если десятков, единиц, или какого-то другого разряда не было, то переходили к следующему разряду.
![]()
![]()
![]()
![]() – 1205,
– 1205, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() – 1 023 029
– 1 023 029
Попробуйте сложить эти два числа, зная, что более 9 одинаковых иероглифов использовать нельзя, и вы сразу поймете, что для работы с этой системой нужен специальный человек. Обычному человеку это не под силу.
В современных жизни люди часто используют египетские иероглифы при оформлении интерьеров различных помещений, в декоре и даже в дизайнерском оформлении компьютерных головоломок.
 |
|||
 |
|||

 2.3. Римская пятеричная
2.3. Римская пятеричная
Это, наверное, самая известная система, после «арабской», она возникла более двух с половиной тысяч лет назад в Древнем Риме.
|
I |
1 |
|
V |
5 |
|
X |
10 |
|
L |
50 |
|
C |
100 |
|
D |
500 |
|
M |
1 000 |
Предполагаемое происхождение римских цифр
 Числа в этой системе, так же как и у нас записывались слева направо, от больших к меньшим. Например, XI = 11, XII = 12, XIII = 13, но следующее число уже особенное, так как такое число «XIIII» писать не удобно, римляне придумали сокращения, они стали писать так XIV = 14, т.е. 10+5-1 = 14. Т.е. если цифра с меньшим значением записывалась перед цифрой с большим значением, то происходило ее вычитание. Так же записывалось число 9 = IX. И кроме этого нельзя было писать четыре одинаковые цифры подряд, например, «XXXX» = XL (50-10) = 40.
Числа в этой системе, так же как и у нас записывались слева направо, от больших к меньшим. Например, XI = 11, XII = 12, XIII = 13, но следующее число уже особенное, так как такое число «XIIII» писать не удобно, римляне придумали сокращения, они стали писать так XIV = 14, т.е. 10+5-1 = 14. Т.е. если цифра с меньшим значением записывалась перед цифрой с большим значением, то происходило ее вычитание. Так же записывалось число 9 = IX. И кроме этого нельзя было писать четыре одинаковые цифры подряд, например, «XXXX» = XL (50-10) = 40.
О происхождении римских цифр достоверных сведений нет. В римской нумерации явственно сказываются следы пятеричной системы счисления. В языке же римлян, ни каких следов пятеричной системы нет. Значит, эти цифры были заимствованы римлянами у другого народа (скорее всего этрусков). Такая нумерация преобладала в Италии до XIII века, а в других странах Западной Европы – до XVI века.
 В Санкт-Петербурге стоит памятник Петру I. На гранитном постаменте памятника есть римское число: MDCCLXXXII = 1000 + 500 + 100 + 100 + 50 + 3*10 + 2 = 1782 год. Это год открытия памятника.
В Санкт-Петербурге стоит памятник Петру I. На гранитном постаменте памятника есть римское число: MDCCLXXXII = 1000 + 500 + 100 + 100 + 50 + 3*10 + 2 = 1782 год. Это год открытия памятника.
Римскими цифрами пользовались очень долго. Еще 200 лет назад в деловых бумагах числа должны были обозначаться римскими цифрами (считалось, что обычные арабские цифры легко подделать). С нею мы достаточно часто сталкиваемся в повседневной жизни. Это номера глав в книгах, указание века, числа на циферблате часов, и т. д.
2.4. Древнегреческая аттическая пятеричная
В древнейшее время в Греции была распространена так называемая Аттическая система счисления, название происходит от области Греции – Аттики со столицей Афины.
В этой системе числа 1, 2, 3, 4 изображались соответствующим количеством вертикальных полосок: ![]() ,
,![]() ,
,![]() ,
,![]() . Число 5 записывалось знаком
. Число 5 записывалось знаком ![]() (древнее начертание буквы «Пи», с которой начиналось слово «пять» – «пенте»). Числа 6, 7, 8, 9 обозначались сочетаниями этих знаков:
(древнее начертание буквы «Пи», с которой начиналось слово «пять» – «пенте»). Числа 6, 7, 8, 9 обозначались сочетаниями этих знаков: ![]()
Число 10 обозначалось ![]() - заглавной «Дельта» от слова «дека» – «десять». Числа 100, 1 000 и 10 000 обозначались H, X, M. Числа 50, 500, 5 000 обозначались комбинациями чисел 5 и 10, 5 и 100, 5 и 1 000, а именно:
- заглавной «Дельта» от слова «дека» – «десять». Числа 100, 1 000 и 10 000 обозначались H, X, M. Числа 50, 500, 5 000 обозначались комбинациями чисел 5 и 10, 5 и 100, 5 и 1 000, а именно:

Числа в пределах первого десятка тысяч записывались так:
![]()
2.5. Древнегреческая ионийская десятеричная алфавитная
Примерно в третьем веке до нашей эры аттическая система счисления в Греции была вытеснена другой, так называемой «Ионийской» системой (она возникла в Милеете – греческая малоазиатская колония Ионии). В ней числа 1-9 обозначаются первыми буквами древнегреческого алфавита:
![]() ,
,
числа 10, 20, … 90 изображались следующими девятью буквами:
![]() ,
,
числа 100, 200, … 900 последними девятью буквами:
![]()
Для обозначения тысяч и десятков тысяч пользовались теми же цифрами, но только с добавлением особого значка '. Любая буква с этим значком сразу же становилась в тысячу раз больше.
Для отличия цифр и букв писали черточки над цифрами.
![]()
Древние евреи, арабы и многие другие народы Ближнего Востока имели такие же системы счисления.
При ее помощи можно было просто записать числа до ста миллионов (100 000 000). Эта система по быстроте счета мало отличается от «арабской». И хоть она не позиционная, но в ней есть мультипликативность.
В современной науке эти цифры-буквы имеют широкое применение в математике и физике. Мы все знаем, что π = 3,14…, а не 80, как в древней Греции.
2.6. Славянская глаголическая десятеричная
Эта система была создана для обозначения чисел в священных книгах западных славян. Использовалась она нечасто, но достаточно долго. По организации она в точности повторяет греческую нумерацию. Использовалась она с VIII по XIII в.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Числа записывали из цифр так же слева, направо, от больших к меньшим цифрам. Если десятков, единиц, или какого-то другого разряда не было, то его пропускали. Такая запись числа аддитивная, то есть в ней используется только сложение:
![]()
![]()
![]() = 800+60+3 = 863
= 800+60+3 = 863
Для того чтобы не перепутать буквы и цифры, использовались титла – горизонтальные черточки над числами, или точки.
2.7. Славянская кириллическая десятеричная алфавитная
Эта нумерация была создана вместе со славянской алфавитной системой для перевода священных библейских книг для славян греческими монахами братьями Кириллом и Мефодием в IX веке. Эта форма записи чисел получила большое распространение в связи с тем, что имела полное сходство с греческой записью чисел. До XVII века эта форма записи чисел была официальной на территории современной России, Белоруссии, Украины, Болгарии, Венгрии, Сербии и Хорватии. До сих пор православные церковные книги используют эту нумерацию.


Числа записывали из цифр так же слева, направо, от больших к меньшим. Числа от 11 до 19 записывались двумя цифрами, причем единица шла перед десятком:
![]()
Читаем дословно «четырнадцать» – «четыре и десять». Как слышим, так и пишем: не 10+4, а 4+10, – четыре и десять. Числа от 21 и выше записывались наоборот, сначала писали знак полных десятков.
Запись числа, использованная славянами аддитивная, то есть в ней используется только сложение:
![]() = 800+60+3
= 800+60+3
Для того чтобы не перепутать буквы и цифры, использовались титла - горизонтальные черточки над числами, что мы видим на рисунке.
Для обозначения чисел больших, чем 900 использовались специальные значки, которые дорисовывались к букве. Так образовывались числа:
|
|
Тысяча |
1000 |
|
|
Тьма |
10 000 |
|
|
Легион |
100 000 |
|
|
Леодр |
1 000 000 |
|
|
Ворон |
10 000 000 |
|
|
Колода |
100 000 000 |
Славянская нумерация просуществовала до конца XVII столетия, пока с реформами Петра I в Россию из Европы не пришла позиционная десятичная система счисления.
2.8. Древнеиндийские системы счисления
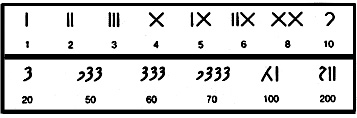
Система счисления кхарошти имела хождение в Индии между VI веком до нашей эры и III веком нашей эры. Эта была непозиционная аддитивная система счисления. О ней мало что известно, так как сохранилось мало письменных документов той эпохи. Система кхарошти интересна тем, что в качестве промежуточного этапа между единицей и десятью выбирается число четыре. Числа записывались справа налево.
Наряду с этой системой существовала в Индии еще одна система счисления брахми.
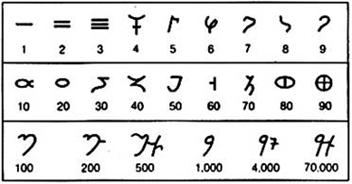
Числа брахми записывались слева направо. Однако в обеих системах было не мало общего. В частности первые три цифры очень похожи. Общим было то, что до сотни применялся аддитивный способ, а после мультипликативный. Важным отличием цифр брахми, было то, что цифры от 4 до 90, были представлены только одним знаком. Эта особенность цифр брахми в дальнейшем была использована при создании в Индии позиционной десятичной системы. В древней Индии так же была словесная система счисления. Она была мультипликативная, позиционная. Знак нуля произносился как «пустое», или «небо», или «дыра». Единица как «луна», или «земля». Двойка как «близнецы», или «глаза», или «ноздри», или «губы». Четыре как «океаны», «стороны света». Например, число 2441 произносилось так: глаза океанов стороны света луны.
3. Недостатки непозиционной системы счисления
Непозиционные системы счисления имеют ряд существенных недостатков:
1. Существует постоянная потребность введения новых знаков для записи больших чисел.
2. Невозможно представлять дробные и отрицательные числа.
3. Сложно выполнять арифметические операции, так как не существует алгоритмов их выполнения. В частности, у всех народов наряду с системами счисления были способы пальцевого счета, а у греков был счетная доска абак – что-то наподобие наших счетов.
Но мы до сих пор пользуемся элементами непозиционной системы счисления в обыденной речи, в частности, мы говорим сто, а не десять десятков, тысяча, миллион, миллиард, триллион.
Список использованных источников
1. Левшин В. Три дня в Карликании. – М., 1966.
2. Всевозможные нумерации и системы счисления (http://www.megalink.ru/~agb/n/numerat.htm)
3. Юшкевич А.П. История математики. – М., Т. 1. – 1970.
4. Глейзер Г.И. История математики в школе. – М., 1964.
5. Депман И.Я. История арифметики. – М., 1965.
6. Костинский А., Губайловский В. Триединый нуль (http://www.svoboda.org/programs/sc/2004/sc.011304.asp)
7. Кузьмищев В.А. Тайна жрецов майя. 2-е изд. – М.: Молодая гвардия, 1975.
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||





