научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 06, июнь 2009
УДК 621.396.679.4
МГТУ им. Н. Э. Баумана
Коллиматорный метод заключается в измерении характеристик направленности антенны, расположенной в поле, близком по структуре к полю плоской волны и создаваемом вспомогательной антенной – коллиматором, расположенным в непосредственной близости от испытуемой антенны, фактически в ближней зоне. Под ближней зоной подразумевается область пространства, расположенная между зоной реактивного поля и зоной дифракции Френеля, то есть ближняя зона характеризуется расстояниями до раскрыва антенны, лежащими в диапазоне от (1...3)![]() до
до ![]() , где
, где ![]() - максимальный поперечный размер раскрыва антенны. Качество коллиматорных стендов в первую очередь определяется величинами отклонений фаз и амплитуд поля в рабочей зоне (вблизи фокальной плоскости зеркала или вблизи раскрыва линзы) от равномерного и синфазного распределений. Область, в которой величины этих отклонений лежат в допустимых пределах, называется рабочей зоной коллиматора. В используемых на сегодняшний день коллиматорных стендах диаметр рабочей зоны в поперечной плоскости составляет не более (30…40)% от диаметра раскрыва зеркала коллиматора. При этом стоимость стенда во многом определяется стоимостью зеркала коллиматора, таким образом, актуальной представляется задача расширения рабочей зоны коллиматоров.
- максимальный поперечный размер раскрыва антенны. Качество коллиматорных стендов в первую очередь определяется величинами отклонений фаз и амплитуд поля в рабочей зоне (вблизи фокальной плоскости зеркала или вблизи раскрыва линзы) от равномерного и синфазного распределений. Область, в которой величины этих отклонений лежат в допустимых пределах, называется рабочей зоной коллиматора. В используемых на сегодняшний день коллиматорных стендах диаметр рабочей зоны в поперечной плоскости составляет не более (30…40)% от диаметра раскрыва зеркала коллиматора. При этом стоимость стенда во многом определяется стоимостью зеркала коллиматора, таким образом, актуальной представляется задача расширения рабочей зоны коллиматоров.
Оптимизация коллиматорного стенда непосредственно связана с исследованием полей в ближней зоне апертурных антенн. Упрощения, которые могут быть допустимы при анализе полей в промежуточной и дальней зонах, оказываются неприемлемыми в ближней зоне. В результате решить задачу синтеза поля с требуемыми характеристиками в рабочей зоне коллиматора, т.е. найти соответствующее распределение токов на поверхности зеркала только строгими аналитическими методами не представляется возможным. Однако существуют приближенные выражения, позволяющие записать поле в ближней зоне в удобном для дальнейших преобразований виде [1]. Конечно, решения, основанные на таких выражениях, также являются приближенными, тем не менее, использование подобных выражений совместно с численными методами позволяет получить достаточно хорошие результаты. При этом численные методы используются для проверки и дальнейшей оптимизаций приближенных решений.
Для нахождения квазиоптимального распределения токов по поверхности зеркального коллиматора был использован подход, аналогичный примененному при рассмотрении плоского (линзового) коллиматора [2]. Поле коллиматора в рабочей зоне представляется как сумма полей равномерно и синфазно возбужденных колец, совокупность которых аппроксимирует зеркало коллиматора. Решение задачи сводится к нахождению амплитуд поля каждого из этих равномерно возбужденных колец с использованием приближенного выражения, полученного в [1]. Данное выражение позволяет определить напряженность поля, создаваемую круглой равномерно и синфазно возбужденной апертурой в точке наблюдения. Поэтому поле каждого из колец, используемых в нашем случае, представляется как разность полей, создаваемых апертурами, диаметр которых соответствует внешнему и внутреннему радиусам кольца. Результирующее поле в точке наблюдения записывается в виде:
![]() , (1)
, (1)
где 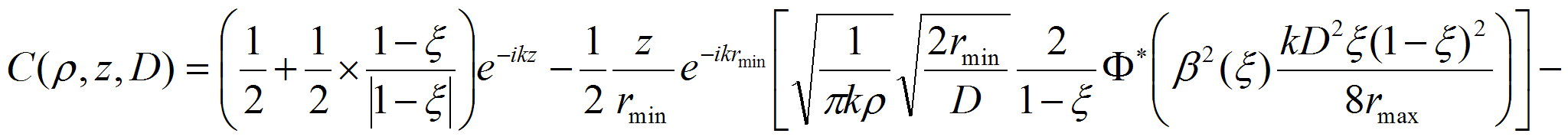
 ; (2)
; (2)
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() и
и ![]() – внешний и внутренний диаметры j-го кольца;
– внешний и внутренний диаметры j-го кольца; ![]() - амплитуда возбуждения j-го кольца.
- амплитуда возбуждения j-го кольца.
При этом стоящая под знаком суммы функция определяет поле, создаваемое j-ым кольцом в i-ой точке наблюдения, расположенной на расстоянии ![]() от оси системы и
от оси системы и ![]() от плоскости апертуры.
от плоскости апертуры.
Если задать постоянное значение напряженности поля для всех точек рабочей зоны диаметром ![]() и затем записать получившееся выражение в матричном виде, то приходим к следующей системе линейных алгебраических уравнений (СЛАУ):
и затем записать получившееся выражение в матричном виде, то приходим к следующей системе линейных алгебраических уравнений (СЛАУ):
 , (3)
, (3)
где ![]() .
.
Считая структуру поля в рабочей зоне осесимметричной, для решения СЛАУ возьмем те точки в рабочей зоне, которые лежат на одной радиальной линии, причем количество точек должно соответствовать количеству равномерно возбужденных колец ![]() . Решение находим, перемножив матрицу, обратную
. Решение находим, перемножив матрицу, обратную ![]() , на матрицу значений амплитуд поля в точках рабочей зоны диаметром
, на матрицу значений амплитуд поля в точках рабочей зоны диаметром ![]() :
:
![]() . (4)
. (4)
В результате получаем значения амплитуд полей равномерно возбужденных колец ![]() . Так как число колец конечно и равно
. Так как число колец конечно и равно ![]() , а диаметры двух соседних колец отличаются на величину постоянного шага
, а диаметры двух соседних колец отличаются на величину постоянного шага ![]() , то после суммирования полей всех колец распределение на поверхности зеркала получается ступенчатым с шагом
, то после суммирования полей всех колец распределение на поверхности зеркала получается ступенчатым с шагом ![]() и должно аппроксимироваться некоторой гладкой функцией. Найденное таким образом решение системы уравнений (3) не дает четкого ответа на вопрос, каким именно должно быть оптимальное распределение токов (поля) на поверхности зеркала коллиматора, однако позволяет сузить пределы поиска квазиоптимального распределения численным методом.
и должно аппроксимироваться некоторой гладкой функцией. Найденное таким образом решение системы уравнений (3) не дает четкого ответа на вопрос, каким именно должно быть оптимальное распределение токов (поля) на поверхности зеркала коллиматора, однако позволяет сузить пределы поиска квазиоптимального распределения численным методом.
Численная оптимизация полученного распределения проводится с использованием алгоритма, основанного на токовом методе. Исходными данными для алгоритма являются: ДН облучателя; выбранная поляризация; координаты фазового центра облучателя; координаты поверхности зеркала; и координаты точек рабочей зоны коллиматора, в которых необходимо рассчитать вектор напряженности электрического поля ![]() . Используя перечисленные исходные данные, алгоритм на основе метода поверхностных токов позволяет рассчитать все три составляющие (две поперечные и продольную) вектора напряженности электрического поля
. Используя перечисленные исходные данные, алгоритм на основе метода поверхностных токов позволяет рассчитать все три составляющие (две поперечные и продольную) вектора напряженности электрического поля ![]() в рабочей зоне коллиматорного стенда.
в рабочей зоне коллиматорного стенда.
Поверхность зеркала задается в декартовой системе координат с центром в вершине параболоида совокупностью координат точек, проекции которых на плоскость ![]() расположены в узлах прямоугольной сетки (ось
расположены в узлах прямоугольной сетки (ось ![]() совпадает с осью зеркала и направлена в сторону облучателя). Шаг сетки определяется компромиссом между точностью расчетов и приемлемым объемом вычислений, в частности, для алгоритма расчета поля в рабочей зоне коллиматора шаг составил величину, равную
совпадает с осью зеркала и направлена в сторону облучателя). Шаг сетки определяется компромиссом между точностью расчетов и приемлемым объемом вычислений, в частности, для алгоритма расчета поля в рабочей зоне коллиматора шаг составил величину, равную ![]() .
.
В соответствии с методом, сначала рассчитываются амплитуда и фаза электрического поля, создаваемого облучателем в точке ![]() , расположенной на зеркале:
, расположенной на зеркале:
![]() . (5)
. (5)
Здесь ![]() – комплексная ДН облучателя;
– комплексная ДН облучателя;
![]() ,
, ![]() – углы, характеризующие направление из фазового центра облучателя в точку
– углы, характеризующие направление из фазового центра облучателя в точку ![]() ;
; ![]() - расстояние от фазового центра до точки
- расстояние от фазового центра до точки ![]() ;
;
![]() - волновое число.
- волновое число.
Мы рассматриваем среду без потерь, следовательно, амплитуда и фаза вектора напряженности магнитного поля рассчитываются следующем образом:
 .
.
Далее в соответствии с поляризацией определяется направление вектора напряженности магнитного поля, а затем его касательная к поверхности параболоида составляющая, так как именно она создает электрический ток на зеркале. Найдем вектор плотности тока в точке ![]() :
:
![]() , (6)
, (6)
где ![]() – нормаль к поверхности зеркала в точке
– нормаль к поверхности зеркала в точке ![]() , обращенная в сторону фокальной плоскости.
, обращенная в сторону фокальной плоскости.
Таким образом, мы получим набор точек ![]() , расположенных на зеркале, и соответствующий этим точкам набор векторов токов:
, расположенных на зеркале, и соответствующий этим точкам набор векторов токов:
![]() , (7)
, (7)
где ![]() – вектор амплитуды плотности тока в точке
– вектор амплитуды плотности тока в точке ![]() .
.
Данный алгоритм используется для расчета поля коллиматора, следовательно, подразумевается большой электрический размер зеркала, а также низкий уровень поля вблизи его кромок, ввиду этого не учитываются дополнительные токи вблизи кромок, введенные П. Я. Уфимцевым.
|
|
|
Рис. 1. К расчету токов на поверхности зеркала. |
После того как найдено амплитудно-фазовое распределение токов по зеркалу, выполняется расчет соответствующего поля в рабочей зоне коллиматора. Воспользуемся частным случаем формулы Кирхгофа и представим токи, текущие по зеркалу как набор дискретных источников тока, расположенных внутри сферы бесконечного радиуса. Вектор тока, характеризующий источник излучения, ![]() направлен по касательной к поверхности зеркала в соответствующей точке
направлен по касательной к поверхности зеркала в соответствующей точке ![]() . Такой источник имеет диаграмму направленности (ДН) вида
. Такой источник имеет диаграмму направленности (ДН) вида ![]() , где
, где ![]() - угол между направлением
- угол между направлением ![]() в точку наблюдения
в точку наблюдения ![]() и нормалью
и нормалью ![]() к поверхности зеркала в точке
к поверхности зеркала в точке ![]() . При этом источник
. При этом источник ![]() излучает электромагнитную волну только в направлении углов
излучает электромагнитную волну только в направлении углов![]() .
.
|
|
|
Рис. 2. К расчету поля в рабочей зоне коллиматора. |
Для расчета поля в рабочей зоне коллиматора, создаваемого такими источниками, воспользуемся частным случаем скалярной формулы Кирхгофа и добавочным криволинейным интегралом Коттлера по кромке зеркала.
Запишем с точностью до постоянного сомножителя проекцию вектора напряженности поля в точке наблюдения ![]() , расположенной в рабочей зоне, на ось
, расположенной в рабочей зоне, на ось ![]() :
:
![]() , (8)
, (8)
где ![]() - проекция вектора
- проекция вектора ![]() на ось
на ось ![]() .
.
Интеграл Коттлера можно записать следующим образом [3]:
![]() , (9)
, (9)
где ![]() – контур зеркала;
– контур зеркала; ![]() – вектор напряженности магнитного поля, создаваемого облучателем в точке, расположенной на контуре;
– вектор напряженности магнитного поля, создаваемого облучателем в точке, расположенной на контуре; ![]() – единичный вектор, направленный по касательной к контуру
– единичный вектор, направленный по касательной к контуру ![]() ;
;
Ввиду дискретности рассматриваемого алгоритма, контур заменяется набором точек ![]() , расположенных на кромках зеркала (шаг составляет
, расположенных на кромках зеркала (шаг составляет![]() ). Далее с точностью до постоянного множителя определим проекцию вектора
). Далее с точностью до постоянного множителя определим проекцию вектора ![]() , на ось
, на ось ![]() , заменив интеграл по контуру суммой:
, заменив интеграл по контуру суммой:
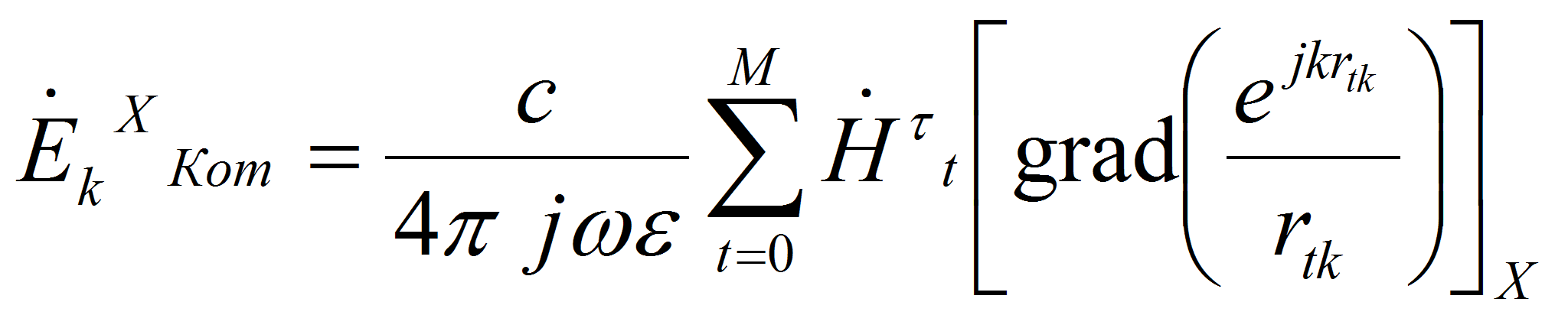 , (10)
, (10)
где ![]() – проекция вектора
– проекция вектора ![]() в точке
в точке ![]() на касательный к контуру в данной точке вектор
на касательный к контуру в данной точке вектор ![]() .
.
В результате проекцию на ось ![]() итогового вектора напряженности электрического поля
итогового вектора напряженности электрического поля ![]() в точке
в точке ![]() можно представить в виде суммы соответствующих составляющих поля, определенных с помощью скалярной формулы Кирхгофа (8)
можно представить в виде суммы соответствующих составляющих поля, определенных с помощью скалярной формулы Кирхгофа (8) ![]() и интеграла Коттлера (10)
и интеграла Коттлера (10) ![]() :
:
 (11)
(11)
Аналогичным образом определяются и остальные составляющие вектора напряженности электрического поля ![]() в рабочей зоне коллиматора. В результате мы определили все три проекции вектора напряженности электрического поля в рабочей зоне: величину главной поляризационной составляющей, кроссполяризационной составляющей, а также характерной для ближней зоны продольной составляющей поля.
в рабочей зоне коллиматора. В результате мы определили все три проекции вектора напряженности электрического поля в рабочей зоне: величину главной поляризационной составляющей, кроссполяризационной составляющей, а также характерной для ближней зоны продольной составляющей поля.
Используемый для алгоритмизации метод Кирхгофа-Коттлера относительно прост и, в то же время, позволяет рассчитать поле в рабочей зоне коллиматора с достаточно высокой точностью.
Данный алгоритм используется для проверки и оптимизации результатов, полученных на основе выражения (4). Выбирается ДН облучателя, создающая поле на поверхности зеркала близкое к полю найденному с помощью (4), а затем ДН корректируется численным методом с тем, чтобы получить такое амплитудное и фазовое распределение токов на резервном участке зеркала, которое позволит максимально расширить рабочую зону коллиматора.
Представленный здесь подход был использован для нахождения квазиоптимального распределения поля по поверхности офсетного коллиматора с электрическим размеров ![]() и фокусным расстоянием
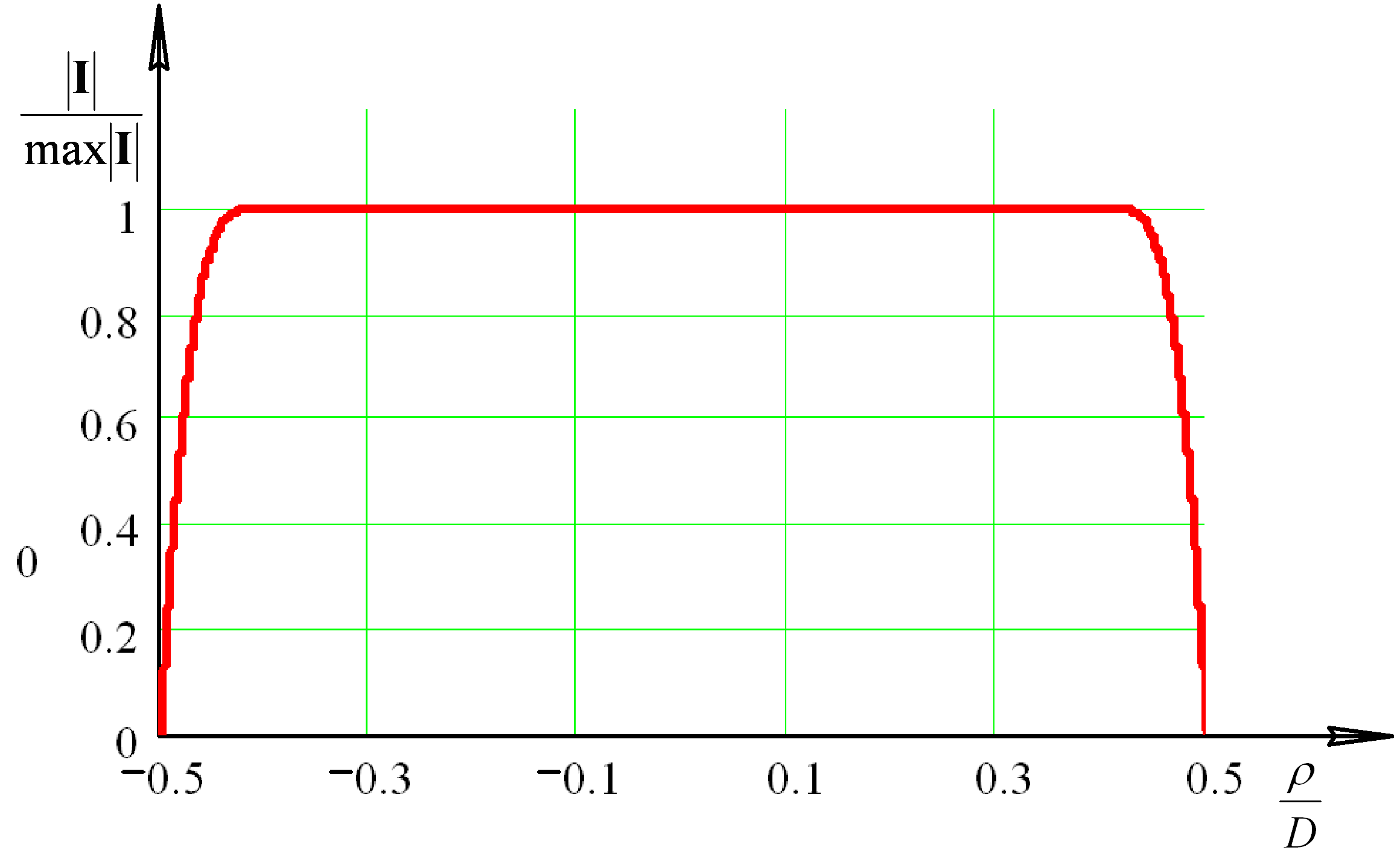
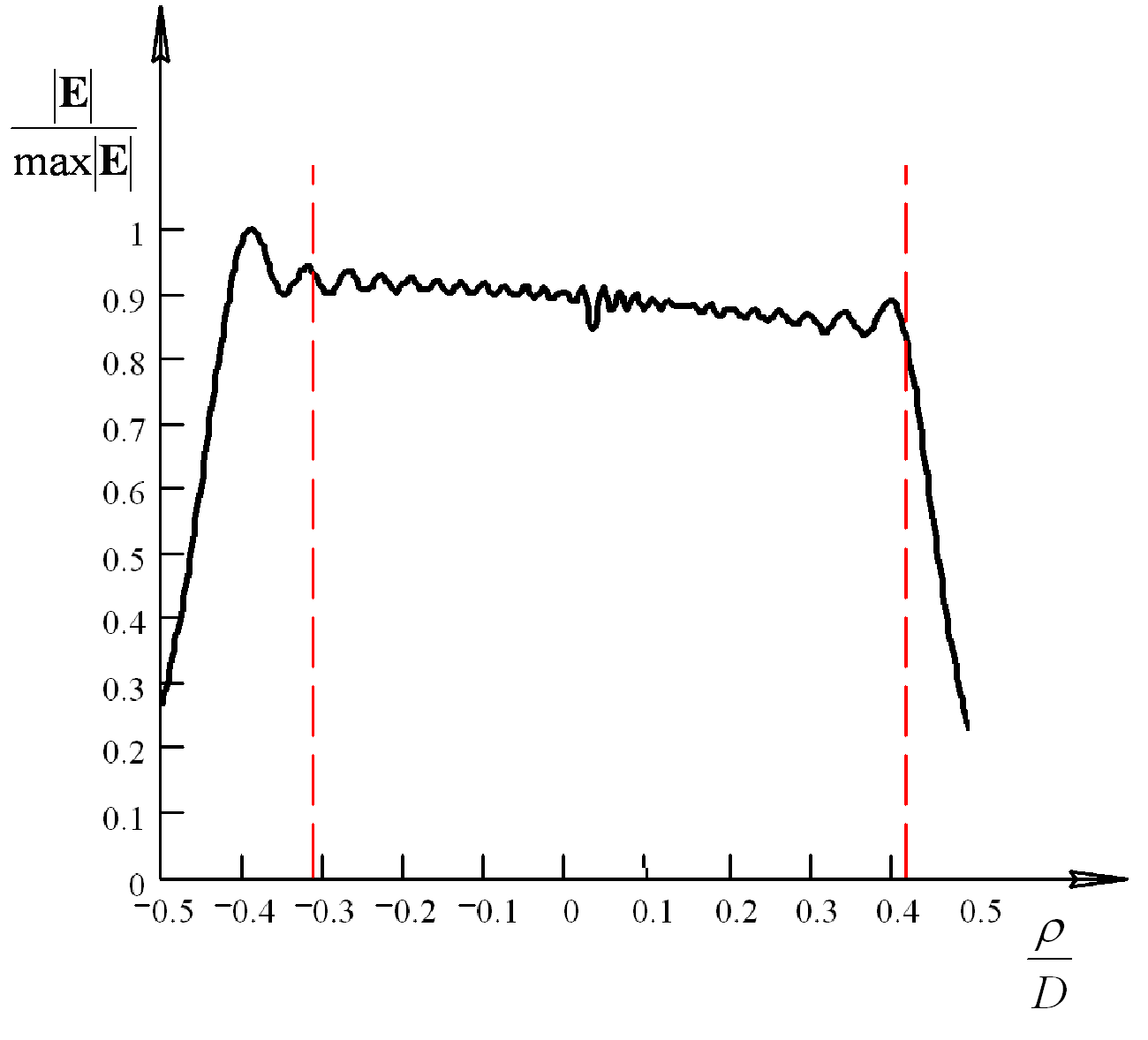
и фокусным расстоянием ![]() . На рисунке 3 изображено амплитудное распределение токов, полученное с помощью формулы (4) и аппроксимированное гладкой гиперболической функцией. Соответствующее распределение поля в рабочей зоне для вертикального сечения, рассчитанное методом поверхностных токов, представлено на рисунке 4 и имеет значительные амплитудные осцилляции поля в центре и на краях рабочей зоны, а также ярко выраженный спад, обусловленный несимметричностью зеркала.
. На рисунке 3 изображено амплитудное распределение токов, полученное с помощью формулы (4) и аппроксимированное гладкой гиперболической функцией. Соответствующее распределение поля в рабочей зоне для вертикального сечения, рассчитанное методом поверхностных токов, представлено на рисунке 4 и имеет значительные амплитудные осцилляции поля в центре и на краях рабочей зоны, а также ярко выраженный спад, обусловленный несимметричностью зеркала.
|
|
|
|
Рис. 3. Амплитудное распределение токов по поверхности коллиматора. |
Рис. 4. Поле в рабочей зоне коллиматора. |
Чтобы избавиться от указанных недостатков численным методом было найдено амплитудное распределение, компенсирующее спад амплитуды поля в рабочей зоне (на рисунке 5: ![]() - угол между горизонтальной плоскостью и плоскостью сечения, в которой представлено распределение токов по зеркалу), а также специальная корректирующая фазовая функция (рис. 6.) на резервном участке зеркала, позволяющая избавиться от осцилляций поля в центре и на краях рабочей зоны. В результате, значение фазы тока в
- угол между горизонтальной плоскостью и плоскостью сечения, в которой представлено распределение токов по зеркалу), а также специальная корректирующая фазовая функция (рис. 6.) на резервном участке зеркала, позволяющая избавиться от осцилляций поля в центре и на краях рабочей зоны. В результате, значение фазы тока в
|
|
|
|
Рис. 5. Квазиоптимальное амплитудное распределение токов по поверхности коллиматора. |
Рис. 6. Корректирующая фазовая функция. |
каждой точке поверхности зеркала такого коллиматора определяется суммой двух составляющих. Первая составляющая определяется расстоянием от текущей точки на зеркале до фазового центра облучателя (то есть зависит от диаметра раскрыва зеркала и его фокусного расстояния), а вторая – значением в данной точке корректирующей фазовой функции. Оптимизированное распределение поля в рабочей зоне для вертикального сечения изображено на рисунке 7.
|
|
|
Рис. 7. Оптимизированное распределение поля в рабочей зоне коллиматора |
Литература
1. Беляев Б. Г. Синтез апертуры плосковолнового устройства компактного полигона. – Сб. Антенны, 1988, вып.35, с.25-34.
2. Семенов К. А. Синтез квазиоптимального распределения поля в рабочей зоне коллиматора. – Радиолокация и связь, 2009, ╧7.
3. Виноградова М. Б., Руденко О. В., Сухоруков А. П. Теория волн. – М.: Наука. Главная редакция физико-математической литературы, 1979.
Публикации с ключевыми словами: Зеркальный коллиматор, АМПЛИТУДНО-ФАЗОВОЕ РАСПРЕДЕЛЕНИЕ, КВАЗИОПТИМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ПОЛЯ
Публикации со словами: Зеркальный коллиматор, АМПЛИТУДНО-ФАЗОВОЕ РАСПРЕДЕЛЕНИЕ, КВАЗИОПТИМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ПОЛЯ
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||