научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 02, февраль 2009
УДК 681.2.087;004.942.519.876.5
МГТУ им.Н.Э.Баумана, Тайвань
K_mt4@org.bmstu.ru
Анализ экспериментальных результатов, представляемых соотношениями вида
![]() (1)
(1)
или ![]() (2)
(2)
с целью определения величин ![]() ,
, ![]() ,
, ![]() ,
, ![]() , по экспериментально регистрируемым зависимостям
, по экспериментально регистрируемым зависимостям ![]() относится к известному классу задачу Прони [1].
относится к известному классу задачу Прони [1].
К первоначальным вариантам постановки задач можно отнести предположение самого Прони об экспоненциальном законе убывания давления в потоке расширяющегося газа, а также проблему анализа состава распадающейся смеси радиоактивных компонентов.
Материал, (например, многокомпонентный композит), испытывающий перестройку его внутренней структуры в результате применения к нему комплекса технологических воздействий, оказывается в термодинамически неравновесном состоянии, а затем постепенно приходит к термодинамическому равновесию.
При этом материал, полученной заготовки на протяжении переходного процесса может обладать несколькими временами релаксации. [2],[3]. Измерительный контроль состояния материала, претерпевающего такого рода переходный процесс, может представить практический интерес.
В связи с этим в данной работе выполнено имитационное математическое моделирование отклика термодинамически неравновесного материала на внешние тестовые воздействия с определением парциальных составляющих (мод) этого отклика, соответствующих различным значениям времени релаксации.
§ 1. Монотонная экспоненциально затухающая релаксация.
Пусть результирующий отклик на внешнее воздействие получен экспериментально и в результате его регистрации получен график представленный на Рис.1

Рис.1 Монотонная экспоненциальная релаксация
Приведенному на графике результирующему отклику соответствует сумма релаксирующих с различными характерными временами составляющих :
![]() (1.1)
(1.1)
В данной постановке задачи наблюдаемыми величинами, регистрируемыми экспериментально, являются значения величины результирующего отклика в различные моменты времени ![]() -
- ![]() и погрешности их определения
и погрешности их определения ![]() . Определению подлежат величины
. Определению подлежат величины ![]() и
и ![]() . Дальнейший рассмотрение ограничивается случаем
. Дальнейший рассмотрение ограничивается случаем ![]() .
.
Из соотношения (1.1) получается
![]() . (1.2)
. (1.2)
Если предположить, что ![]() распределены в порядке возрастания по закону
распределены в порядке возрастания по закону ![]() , то все значения
, то все значения ![]() положительны и при
положительны и при ![]() справедливо
справедливо
![]() (1.3)
(1.3)
Очевидно, величина ![]() может быть установлена перебором значений
может быть установлена перебором значений ![]() . Так как зависимость
. Так как зависимость ![]() получена экспериментально и обладает погрешностями, непосредственное использование соотношения (1.3) может привести к неконтролируемому нарастанию погрешностей.
получена экспериментально и обладает погрешностями, непосредственное использование соотношения (1.3) может привести к неконтролируемому нарастанию погрешностей.
Соотношению (1.3) соответствует с учетом погрешностей входящих в него параметров выражение
![]() , (1.4)
, (1.4)
с учетом справедливого при ![]() (
(![]() - продолжительность времени наблюдения) приближения
- продолжительность времени наблюдения) приближения ![]() окончательный результат:
окончательный результат:
![]() (1.5)
(1.5)
здесь ![]() погрешность определения величины
погрешность определения величины ![]() находится численно графически в процессе перебора значений параметра
находится численно графически в процессе перебора значений параметра ![]() по вариациям графиков зависимости
по вариациям графиков зависимости ![]() , при
, при ![]() .
.
Аналогичным образом определяются значения ![]() ,
, ![]() ,
, ![]() ,
, ![]() , с использованием зависимости
, с использованием зависимости
![]() (1.6)
(1.6)
В результате получается
![]() (1.7)
(1.7)
![]() (1.8)
(1.8)
Для третьего слагаемого справедливы соотношения
![]() (1.9)
(1.9)
![]() (1.10)
(1.10) ![]() (1.11)
(1.11)
Для последнего слагаемого справедливо
![]() (1.12)
(1.12)
![]() (1.13)
(1.13)
Таким образом, проведенное численно-графическое исследование показывает, что погрешность определения параметров исходной зависимости последовательно накапливается и необходимы меры по максимальному снижению погрешностей исходных данных, получаемых в результате измерений.
§ 2. Осциллирующая экспоненциально затухающая релаксация отклика.
Для реализации математической имитации процедуры анализа составляющих экспериментально зарегистрированного процесса вида
 (2.1)
(2.1)
задаются исходные о параметрах ![]() ,
, ![]() ,
, ![]() ,
, ![]() , (
, (![]() ) сведенное в таблицу 1
) сведенное в таблицу 1
таблица 1
|
Номер параметры |
1 |
2 |
3 |
4 |
|
|
1.3 |
1.5 |
1.7 |
2 |
|
|
0.3 |
0.4 |
0.5 |
0.6 |
|
|
2π |
3π |
4π |
5π |
|
|
|
|
|
|
Исходное соотношение (2.1) подвергается зашумлению и его результат представлен на графике Рис.2.
Зашумленные исходные данные подвергается сглаживанию с помощью фильтров Савицкого-Голея.

Рис.2. Осциллирующая экспоненциальная релаксация отклика
Сглаживающие фильтры Савицкого—Голея, также называемые полиномиальными сглаживающими фильтрами или сглаживающими фильтрами с минимальной квадратической ошибкой, как правило, используются для «сглаживания» зашумленных сигналов с широким (без шума) спектром. В данном случае сглаживающие фильтры Савицкого—Голея работают намного лучше обычных усредняющих нерекурсивных фильтры, которые имеют тенденцию вместе с шумом удалять значительную долю высокочастотных составляющих сигнала. Фильтры Савицкого—Голея лучше сохраняют высокочастотные компоненты сигнала, однако обеспечивают худшее подавление шума по сравнению с обычными нерекурсивными фильтрами. график представлен на Рис.3.
![]() (2.2)
(2.2)

Рис.3. фильтрация фильтром Савицкого-Голея
Полагается, что как и в предыдущем параграфе, параметры ![]() , характеризующие затухание гармоник , образуют последовательность
, характеризующие затухание гармоник , образуют последовательность
![]() (2.3)
(2.3)
Это позволяет перебором величин параметра ![]() , в интервале
, в интервале ![]() привести зависимость
привести зависимость ![]() к виду
к виду
 (2.4)
(2.4)
Для определения значения параметра ![]() вычисляются последовательности интегралов
вычисляются последовательности интегралов
 (2.5)
(2.5)
Где параметр ![]() принимает значения
принимает значения ![]() для различных пробных вариантов. Рис.4.
для различных пробных вариантов. Рис.4.
Рассмотрение графиков на Рис.3. и Рис.4. позволяет выделить области ![]() и
и ![]() для определения циклической частоты
для определения циклической частоты ![]() и амплитуды
и амплитуды ![]() соответственно. Рис.5.
соответственно. Рис.5.

Рис.4. для различных пробных вариантов
Значение ![]() определяется с подошью преобразования Фурье (Рис.5) и оказывается равным
определяется с подошью преобразования Фурье (Рис.5) и оказывается равным ![]() . для амплитуды
. для амплитуды ![]() находится предварительное значение. (Рис.6.
находится предварительное значение. (Рис.6. ![]() .)
.)
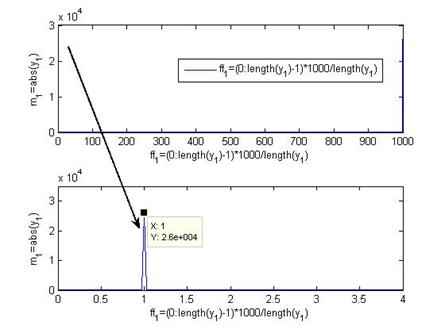
Рис.5. преобразования Фурье ![]()
Этот результат получается выделением в области ![]() , значений минимально отклоняющихся амплитуд колебаний при переборе значений
, значений минимально отклоняющихся амплитуд колебаний при переборе значений ![]() , которое определяется при этом одновременно .
, которое определяется при этом одновременно .
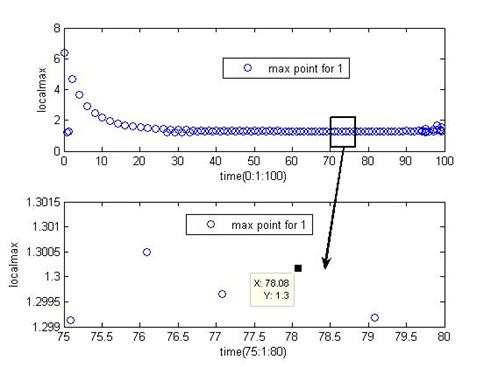
Рис.6 предварительное значение амплитуды ![]() .
.
Значение фазы ![]() определяется из последовательности величин, получаемых численными расчетами на интервала
определяется из последовательности величин, получаемых численными расчетами на интервала ![]()
 (2.6)
(2.6)
Вычисление показывает, что при стремлении ![]() к предельному значению, равному 84, величина этого интеграла стабилизируется (Рис.8). это означает , что
к предельному значению, равному 84, величина этого интеграла стабилизируется (Рис.8). это означает , что ![]() .
.
При этом из соотношения (2.5) следует значение 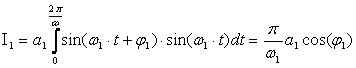 . (2.7)
. (2.7)
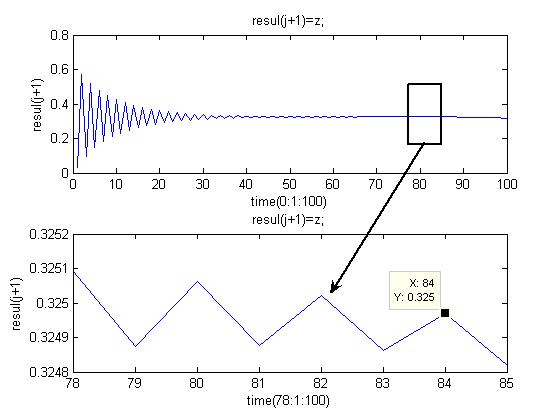
Рис.7. определение значения фазы ![]()
Получив стабилизировавшееся значение интервала ![]() , можно определить значение фазы
, можно определить значение фазы ![]() .
.
 (2.8)
(2.8)
За окончательное и наиболее точное значение амплитуды принимается её величина на последнем периоде в окрестности ![]() .
.
Таким образом, для первого слагаемого выражения (2.1) определены все параметры ![]() ,
, ![]() ,
, ![]() ,
, ![]() сведенные в таблицу 2.
сведенные в таблицу 2.
Таблица. 2
|
|
Исходные значения |
Вычисленные значения |
|
|
0,3 |
0.3 |
|
|
2π |
6.28318 |
|
|
1,3 |
1.29972 |
|
|
|
1.04713 |
Для определения параметров второго слагаемого исходного соотношения (2.2) необходимо выполнить преобразования функции .
![]() (2.9)
(2.9)
График этой функции представлен на Рис.7.

Рис.8 ![]()
В первую очередь подбирается значение параметра ![]() путем анализа поведения функций
путем анализа поведения функций ![]() в зависимости от величины
в зависимости от величины ![]() .
.
Для больших значениях ![]() . вычисления показывают, что при
. вычисления показывают, что при ![]() величины интегралов можно заменить суммами :
величины интегралов можно заменить суммами :
 (2.10)
(2.10)
где ![]()
![]()

Рис.9. путем анализа поведения функций ![]()
Эти суммы уменьшаются с ростом ![]() , то есть с ростом параметра
, то есть с ростом параметра ![]() , С другой стороны, при
, С другой стороны, при ![]() происходит уменьшения значений величины до этих суммы
происходит уменьшения значений величины до этих суммы ![]() , а затем они увеличиваются. Поэтому принимается предварительное значение
, а затем они увеличиваются. Поэтому принимается предварительное значение ![]() .Рис.9.
.Рис.9.
Применение к соотношению (2.9) преобразования Фурье при ![]() позволяет определить параметр
позволяет определить параметр ![]() - циклическую частоту второй убивающейся по амплитуде гармоники.(Рис.10). В результате расчетов получается
- циклическую частоту второй убивающейся по амплитуде гармоники.(Рис.10). В результате расчетов получается ![]() .
.

Рис.10. преобразование Фурье при ![]()
Из графика значений максимума функции ![]() , представленного на Рис.11, можно определить предварительное значение амплитуды
, представленного на Рис.11, можно определить предварительное значение амплитуды ![]() , получаемое как среднее арифметическое 30 величин
, получаемое как среднее арифметическое 30 величин
![]() (2.11)
(2.11)

Рис.11. среднее арифметическое 30 величин ![]()
Уточнение значения величин ![]() ,
, ![]() и определение величины фазы
и определение величины фазы ![]() производиться с помощью соотношения
производиться с помощью соотношения
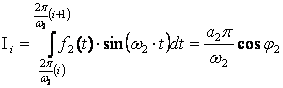 (2.12)
(2.12)
Последовательность значений интегралов представлена на графиках (Рис.11). Из первого видно, что область наиболее стабильных значений фазы соответствует окрестности ![]() .
.
Уточненное значение ![]() получается в окрестности
получается в окрестности ![]() (Рис.12) и оказывается равным
(Рис.12) и оказывается равным ![]() . Сопоставление графиков Рис.11, показывает что уточенному значению
. Сопоставление графиков Рис.11, показывает что уточенному значению ![]() , соответствует диапазон
, соответствует диапазон ![]() , при этом
, при этом
 (2.13)
(2.13)
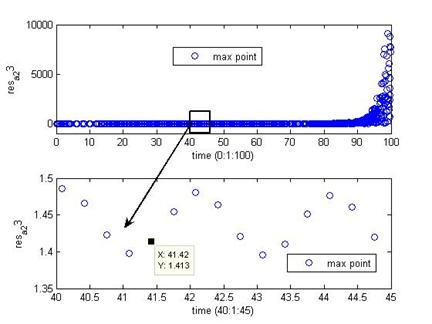
Рис.12. уточненное значение ![]() получается в окрестности
получается в окрестности ![]() .
.
Используя это уточнённое значение ![]() , в следующем из формулы (2.12) соотношении получим уточнённое значение
, в следующем из формулы (2.12) соотношении получим уточнённое значение ![]() .
.
 (2.14)
(2.14)
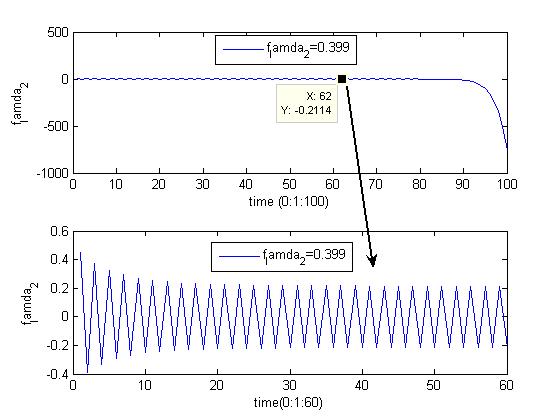
Рис.13. Процедура уточнения величины ![]() и
и ![]()
Процедура уточнения величины ![]() и
и ![]() отражена на графиках Рис.12 и Рис.13.
отражена на графиках Рис.12 и Рис.13.
Таким образом, для второго слагаемого определены все параметры ![]() ,
, ![]() ,
, ![]() ,
, ![]() сведенные в таблицу 2.
сведенные в таблицу 2.
Таблица 2
|
|
Исходные значения |
предварительные значения |
Вычисленные значения |
|
|
0,4 |
0.35 |
0.399 |
|
|
3π |
9.42477 |
9.42477 |
|
|
1.5 |
12.44038 |
1.44126 |
|
|
|
9.42477 |
0.78317 |
Для определения параметров третьего слагаемого исходного соотношения (2.1) необходимо вычислить функцию
![]() (2.15)
(2.15)
График этой функции, представлен на Рис.14.

Рис.14. ![]()
Из полученного графика видно , что при ![]() преобладают помехи, приводящие к росту функции
преобладают помехи, приводящие к росту функции ![]() с увеличением
с увеличением ![]() . на интервале
. на интервале ![]() .
.
На нижнем графике Рис.14 представлено преобразование Фурье для функций ![]() , позволяющие определить величину циклической частоты
, позволяющие определить величину циклической частоты ![]() . Она оказывается равной
. Она оказывается равной ![]() .
.
Для определения предварительного значения параметра ![]() вычисляются последовательности интегралов
вычисляются последовательности интегралов
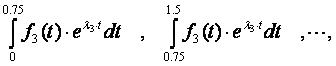 (2.16)
(2.16)
Где параметр ![]() принимает значения
принимает значения ![]() для различных пробных вариантов.
для различных пробных вариантов.

Рис.15. Результаты вычислений ![]()
Результаты вычислений представлены на Рис.15 и Рис.16 в виде последовательностей точек со знакопеременными значениями по оси у

Рис.16. последовательности точки со знакопеременными значениями по оси у
Из графически представленных результатов расчетов видно, что в окрестности значения ![]() монотонное убывающее отклонений от горизонтальной оси, сменяется их возрастанием. поэтому предварительное значение
монотонное убывающее отклонений от горизонтальной оси, сменяется их возрастанием. поэтому предварительное значение ![]() принимается равным 0.44.
принимается равным 0.44.
График функции ![]() при
при ![]() представлен на Рис.17.
представлен на Рис.17.
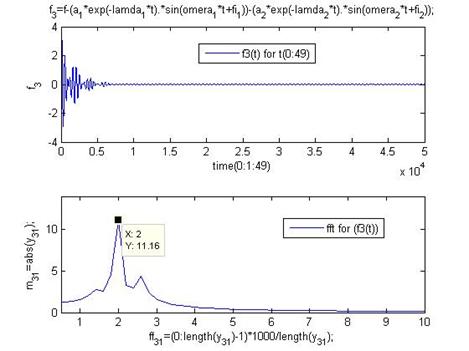
Рис.17. График функции ![]() при
при ![]()
Результаты Фурье-анализа функции ![]() даны на нижем графике Рис.17. Расчеты показали , что
даны на нижем графике Рис.17. Расчеты показали , что ![]() .
.
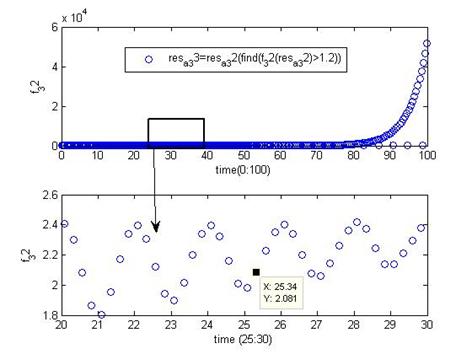
Рис.18. график функции ![]()
Представленный на Рис.18. график функции ![]() позволил установить область максимальной стабильности амплитуды
позволил установить область максимальной стабильности амплитуды ![]() : она приходится на интервал
: она приходится на интервал ![]() .
.
При этом предварительное значение ![]() оказалось равным 0.30069.
оказалось равным 0.30069.
Для получения этого результата вычислялось среднее арифметическое 20. максимальных (амплитудных) значений функции.
 (2.17)
(2.17)
Значения фазы ![]() определялись в результате вычисления интегралов вида :
определялись в результате вычисления интегралов вида :
 (2.18)
(2.18)

Рис.19. отмечена окрестность значения ![]() .
.
На графике Рис.19. отмечена окрестность значения ![]() , где интеграл обладает максимальной стабильностью.
, где интеграл обладает максимальной стабильностью.
Повторяя ранее применявшийся подход, определяем уточненные значения параметров ![]() .
.
Значения ![]() уточняются путем анализа поведения величин интегралов вида (2.18) на интервале
уточняются путем анализа поведения величин интегралов вида (2.18) на интервале ![]() .
.
Результаты расчетов (Рис.20) дают ![]() .
.

Рис.20. Результаты расчетов дают ![]() .
.
Преобразование Фурье функции ![]() на интервале
на интервале ![]() позволяет определить циклическую частоту
позволяет определить циклическую частоту ![]() . В результате оказалось
. В результате оказалось ![]() .(Рис.21).
.(Рис.21).
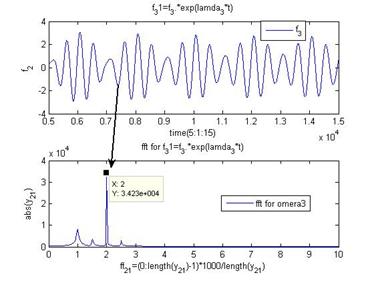
Рис.21 В результате оказалось ![]()
Уточненное значение амплитуды ![]() на интервале
на интервале ![]() оказалось равным
оказалось равным ![]() = 1.46094. При этом определялось среднее арифметическое значение .Рис.22.
= 1.46094. При этом определялось среднее арифметическое значение .Рис.22.
 (2.19)
(2.19)

Рис. 22. среднее арифметическое значение 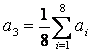
Уточненное значение ![]() определялось из соотношения (2.18). (Рис.23).
определялось из соотношения (2.18). (Рис.23).
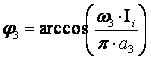 (2.20)
(2.20)
При ![]() получилось
получилось ![]() = 0.28454
= 0.28454
Таким образом, для третьего слагаемого определены все параметры ![]() ,
, ![]() ,
, ![]() ,
, ![]() сведенные в таблицу 3.
сведенные в таблицу 3.
Таблица 3
|
|
Исходные значения |
предварительные значения |
Вычисление значения |
|
|
0.5 |
0.45 |
0.51 |
|
|
4π |
16.07898 |
16.07898 |
|
|
1.7 |
1.46094 |
2.05828 |
|
|
|
6.49862 |
0.28454 |

Рис.23. Уточненное значение ![]()
Для определения погрешностей параметров четвертого слагаемого исходного соотношения (2.2) необходимо вычислить функцию
 (2.21)
(2.21)
График функции ![]() представлен на Рис.24.
представлен на Рис.24.
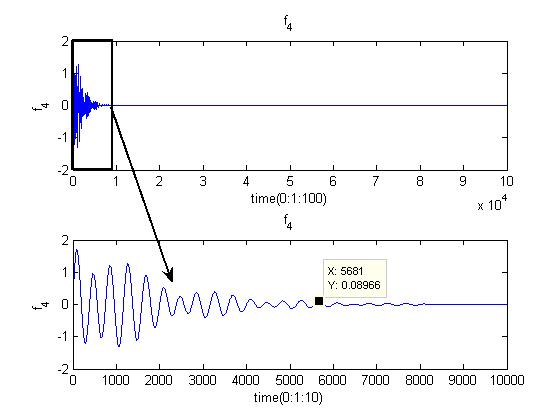
Рис.24. 
![]() (2.22)
(2.22)
График функции ![]() представлен на Рис.25.
представлен на Рис.25.

Рис.25. График функции ![]()
Уравнения (2.21) и (2.22) при времени ![]() представлены на Рис.25.
представлены на Рис.25.
Погрешность можно определить по формуле
![]() (2.23)
(2.23)
График этой функции ![]() представлен на Рис.26.
представлен на Рис.26.

Рис.26. график погрешности определения последнего слагаемого
ЛИТЕРАТУРА
1. Марпл.-мл. С.Л. Цифровой спектральный анализ и его приложения: Пер.с англ.-М.: Мир,1990.-584с.,ил.
2. Постников В.С. Внутреннее трение в металлах.- М.:Изд-во «Металлугия»,1969.-330с.
3. Постников. В.С. Физика и химия твердого состояния, М.: «Металлургия»,1978,-544с.
Публикации с ключевыми словами: имитационное моделирование, релаксационные процессы
Публикации со словами: имитационное моделирование, релаксационные процессы
Смотри также:
- 77-48211/631407 Имитационная модель аксиального индукторного генератора с релейным регулятором напряжения
- Построение модели единой службы аутентификации, авторизации и учета пользователей информационных ресурсов Университета
- Разработка программной среды для моделирования и оптимизации складской политики двухэшелонных многопродуктовых цепей поставки
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



