научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 05, май 2009
МГТУ им. Н.Э. Баумана
Введение
Повышение тепловой мощности активных зон является важным для повышения конкурентоспособности действующих и проектируемых АЭС. Над данной задачей работают многие коллективы организаций атомной отрасли. Предложены и находятся в большой степени проработанности четыре направления повышения тепловой мощности.
· Увеличение загрузки топлива в активной зоне. Например, высота топливного столба в ТВС-2М по сравнению с ТВС-2 увеличена на 150 мм за счет изменения конструкции хвостовика и головки [1].
· Снятие избыточного консерватизма в теплогидравлических и нейтронно-физических расчетах позволило обосновать возможность повышения тепловой мощности до 104% за счет уменьшения коэффициента запаса по линейной мощности [2].
· Введение в кассеты интенсификаторов тепломассообмена с тем, чтобы повысить значения критического теплового потока, увеличить теплосъем с ТВС [1].
· Изменение диаметров твэлов, что требует большого объема НИОКР [2].
Исследование влияния интенсификаторов тепломассообмена на увеличение тепловой мощности ТВС было начато в 70-80 голах прошлого века. Оно базируется на представлении о физической природе кризиса теплообмена при кипении, являющегося главной причиной, ограничивающей тепловую мощность наиболее напряженных ТВС, а следовательно и активной зоны в целом.
Кризис кипения — явление характеризуемое внезапным падением коэффициента теплоотдачи вследствие изменения механизма кипения, что приводит к росту температуры поверхности нагрева. Тепловой поток непосредственно перед наступлением кризиса называется критическим тепловым потоком [3].
На кризис кипения при вынужденном движении потока жидкости влияние оказывают [4] пузырьковый слой, движущийся параллельно поверхности нагрева, который так близко примыкает к поверхности нагрева, что ограждает ее от поступления холодной жидкости, а также неустойчивость потока. Последняя характеризуется тем, что в процессе местных колебаний течения пограничный слой периодически замедляется, а нагретая поверхность под этим временно заторможенном слоем может перегреться, что приводит к преждевременному кризису кипения.
Различают кризис кипения в зоне недогрева потока до состояния насыщения или низкого массового паросодержания. Такой тип кризиса кипения наблюдается только при относительно высоких тепловых потоках, когда возникает такое интенсивное кипение, что пузыри скапливаются возле поверхности нагрева. Величина критического теплового потока в большей степени зависит от параметров пристенной зоны, чем от недогрева основной части потока. Такой тип кризиса кипения называют кризисом кипения первого рода. Именно он характерен для ректоров с водой под давлением.
1. Теоретические подходы к изучению явления кризиса кипения
Одной из первых моделей, позволяющих описать механизм возникновения кризиса кипения, стала модель баланса сил, действующих на пузырь предложенная П. Ченгом [4].
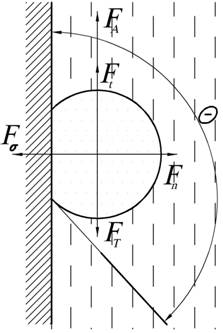
Рис. 1 . Баланс сил, действующих на прикрепленный к стенке пузырь
На пузырь, прикрепленный к вертикальной стенке (рис.1) действуют следующие силы:
·
сила тяжести ![]() ,
где
,
где ![]() —
масса
насыщенного
пара внутри
пузыря,
—
масса
насыщенного
пара внутри
пузыря, ![]() ,
,![]() —
объем и
радиус
пузыря в
момент
отрыва,
—
объем и
радиус
пузыря в
момент
отрыва, ![]() —
плотность
насыщенного
пара,
—
плотность
насыщенного
пара, ![]() —
ускорение
свободного
падения;
—
ускорение
свободного
падения;
·
сила
Архимеда ![]() ,
где
,
где ![]() —
масса
жидкости,
вытесненная
пузырем,
—
масса
жидкости,
вытесненная
пузырем, ![]() —
плотность
жидкости;
—
плотность
жидкости;
·
сила
поверхностного
натяжения ![]() ,
где
,
где ![]() —
длина
контакта
пузыря и
стенки в
момент отрыва,
—
длина
контакта
пузыря и
стенки в
момент отрыва,
![]() —
коэффициент
поверхностного
натяжения,
—
коэффициент
поверхностного
натяжения, ![]() —
коэффициент,
зависящий от
краевого
угла смачивания;
—
коэффициент,
зависящий от
краевого
угла смачивания;
·
сила инерции,
с учетом
поправки на
неинерциальность
системы
пузырь-поток
жидкости, ![]() ,
где
,
где ![]() —
тангенциальная
составляющая
силы инерции
—
тангенциальная
составляющая
силы инерции
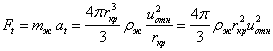 ,
,
![]() —
нормальная
составляющая
силы инерции
—
нормальная
составляющая
силы инерции
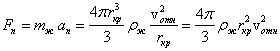 ,
,
![]() ,
, ![]() —
тангенциальная
и нормальная
составляющие
ускорения,
—
тангенциальная
и нормальная
составляющие
ускорения,![]() и
и ![]() —
составляющие
относительной
скорости
между
жидкостью и
пузырем, нормальная
и
параллельная
к стенке
соответственно.
—
составляющие
относительной
скорости
между
жидкостью и
пузырем, нормальная
и
параллельная
к стенке
соответственно.
Система баланса сил, действующих на пузырь вдоль и поперек потока, имеет вид
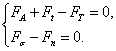
Решение данной системы определяет величину отрывного радиуса пузыря, который оказался обратно пропорционален квадрату относительной скорости, и вычисляется как
![]() .
(1)
.
(1)
Ченг [4] представил критический тепловой поток как сумму количества теплоты, переносимой за счет конвекции жидкости, и скрытой теплоты парообразования, переносимой пузырями
![]() ,
(2)
,
(2)
В
формуле (2) ![]() —
критический
тепловой
поток,
—
критический
тепловой
поток, ![]() ,
,![]() —
постоянные,
—
постоянные, ![]() ,
, ![]() —
нормальные к
стенке
скорости в
момент отделения
пузыря
жидкости и
насыщенного
пара
соответственно,
—
нормальные к
стенке
скорости в
момент отделения
пузыря
жидкости и
насыщенного
пара
соответственно,
![]() —
температура
недогрева,
—
температура
недогрева, ![]() —
температура
насыщения,
—
температура
насыщения, ![]() —
температура
в месте
кризиса,
—
температура
в месте
кризиса, ![]() —
теплота
парообразования.
Скорости
—
теплота
парообразования.
Скорости ![]() и
и
![]() связаны
равенством
связаны
равенством 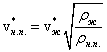 , которое
получено из
условия, что
полное количество
движения
уходящего
пара и поступающей
жидкости
постоянно. С
другой стороны
из
векторного
равенства
, которое
получено из
условия, что
полное количество
движения
уходящего
пара и поступающей
жидкости
постоянно. С
другой стороны
из
векторного
равенства ![]() следует
связь
нормальных к
стенке
скоростей
жидкости и
насыщенного
пара с
нормальной
составляющей
скорости
между
жидкостью и
пузырем.
Последняя
определяется
через число Вебера
и радиус
пузыря в
момент
отрыва и имеет
вид
следует
связь
нормальных к
стенке
скоростей
жидкости и
насыщенного
пара с
нормальной
составляющей
скорости
между
жидкостью и
пузырем.
Последняя
определяется
через число Вебера
и радиус
пузыря в
момент
отрыва и имеет
вид 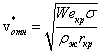 .
.
Хотя Ченг не предложил удовлетворительного метода определения значений постоянных в уравнении (2) для воды, движущейся в канале, он разработал основы анализа кризиса кипения в большом объеме и при вынужденном движении.
Важным этапом для описания механизма возникновения кризиса стало появление модели критического перегрева в пристенном слое жидкости Л. Тонга [4]. Тонг рассмотрел баланс энергии для слоя перегретой жидкости, отделенной от основного потока пузырьковым слоем (рис. 2) и представил его в виде
![]() .
(3)
.
(3)
В
уравнении (3) ![]() —
средняя
плотность
слоя жидкости,
—
средняя
плотность
слоя жидкости,
![]() —
средняя
скорость
слоя
жидкости,
—
средняя
скорость
слоя
жидкости, ![]() —
периметр
нагревателя,
—
периметр
нагревателя, ![]() —
толщина слоя
жидкости,
—
толщина слоя
жидкости, ![]() —
средняя
энтальпия
слоя
жидкости,
—
средняя
энтальпия
слоя
жидкости, ![]() —
энтальпия
насыщенной
жидкости,
—
энтальпия
насыщенной
жидкости, ![]() —
коэффициент
теплоотдачи
от cлоя
жидкости
пузырьковому
слою,
—
коэффициент
теплоотдачи
от cлоя
жидкости
пузырьковому
слою, ![]() —
средняя
удельная теплоемкость
перегретой
жидкости,
—
средняя
удельная теплоемкость
перегретой
жидкости, ![]() —
тепловой
поток от
поверхности,
—
тепловой
поток от
поверхности, ![]() —
расстояние.
—
расстояние.
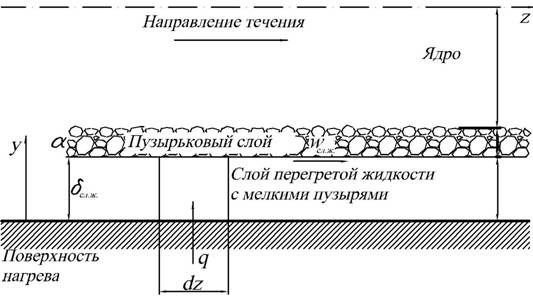
Рис. 2 . Физическая модель слоя перегретой жидкости
между пузырьковым слоем и поверхностью нагрева
Физическая модель Тонга содержит предположение, что энтальпия жидкости, получаемая из баланса энергии слоя перегретой жидкости, является показателем, характеризующим начало кризиса кипения.
Решение уравнения (3) для состояния, близкого к кризису кипения при заданных параметрах (т. е. давлении, массовом расходе, паросодержании и эквивалентном диаметре) и дополнительных упрощениях для однородного (4) и неоднородного (5) теплового потока имеют вид
![]() ,
(4)
,
(4)
![]() .
(5)
.
(5)
Из предположения, что начало кризиса кипения определяется предельным значением энтальпии перегретого слоя, Тонг получил соотношение для эквивалентного однородного теплового потока при кризисе кипения
![]() (6)
(6)
Здесь
коэффициент ![]() зависит
от режима
течения и
паросодержания,
что в
принципе
можно свести
к зависимости
от скорости
зависит
от режима
течения и
паросодержания,
что в
принципе
можно свести
к зависимости
от скорости ![]() ,
которую
можно определить
из
зависимостей
Ченга о связи
отрывного
радиуса
пузыря и
скорости
течения жидкости,
,
которую
можно определить
из
зависимостей
Ченга о связи
отрывного
радиуса
пузыря и
скорости
течения жидкости,
![]() —
положение
точки начала
кризиса
кипения, измеренное
от точки
закипания
недогретой
жидкости. Для
перехода от
эквивалентного
потока к
местному
неоднородному
потоку
вводится
поправочный
коэффициент
—
положение
точки начала
кризиса
кипения, измеренное
от точки
закипания
недогретой
жидкости. Для
перехода от
эквивалентного
потока к
местному
неоднородному
потоку
вводится
поправочный
коэффициент
![]()
или,
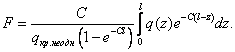 (7)
(7)
Поправочный коэффициент в общем случае также является функцией паросодержания. Соотношения для его определения приведены в книге Тонга [4], а также в работах наших исследователей В.С. Осмачкина [5], В.Н. Смолина [6,7].
2. Эмпирические соотношения для расчета критического теплового потока в реальных конструкциях. Табличный метод ФЭИ.
Не смотря на введении поправочного коэффициента, модели Ченга и Тонга не позволяют провести расчет на кризис кипения реально существующих конструкций, хотя и дают возможность понять сам механизм протекания процесса. Это обусловлено рядом причин:
· сложность геометрии реальных конструкций ТВС, представляющих собой пучки стержней в треугольной (ВВЭР) либо квадратной упаковке (PWR), в которых можно выделить несколько различных видов ячеек рис.3;
· наличие необогреваемых трубок (направляющие каналы и центральная трубка), а, следовательно, разный подогрев в разных ячейках;
· неравномерное энерговыделение по сечению и длине активной зоны, разный расход, перетечки теплоносителя из ячейки в ячейку;
· влияние дистанционирующих и перемешивающих решеток, различающихся по конструкции и имеющих разные гидравлические характеристики.
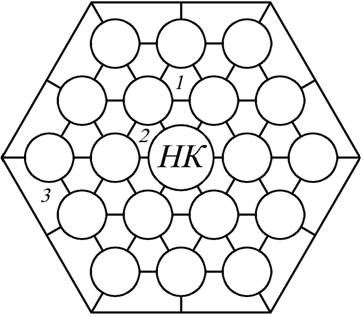
Рис. 3 . Пучок с треугольной упаковкой твэлов.
1- ячейка образована твэлами, 2 – ячейка образована твэлами
и направляющим каналом (НК), 3 – периферийная ячейка
В
своих
моделях ни
Тонг, ни Ченг
этого не
учитывали,
рассматривая
более простые
случаи.
Реальные
конструкции
сложны.
Поэтому для
их расчета
применялись
и применяются
эмпирические
зависимости,
которые дают
хорошие
результаты
только в определенном
диапазоне
параметров:
длина пучка,
гидравлический
диаметр,
давление,
массовая
скорость,
паросодержание.
Например,
зависимость,
предложенная
в 1951 г.
Аргонской
Национальной
лабораторией
(ANL) для
критического
теплового
потока при
кипении с
недогревом
до температуры
насыщения ![]() в
трубе
жидкости с
массовой
скоростью
в
трубе
жидкости с
массовой
скоростью ![]() [4]
, имеет вид
[4]
, имеет вид
![]() .
(8)
.
(8)
Значения
параметров ![]() и
и
![]() ,
при которых
данная
зависимость
верна, приведены
в таблице 1.
,
при которых
данная
зависимость
верна, приведены
в таблице 1.
Таблица 1. Значения параметров с и m в зависимости ANL
|
|
МПа
|
3,5
|
7
|
14
|
|
|
|
0,817
|
0,626
|
0,445
|
|
|
|
0,160
|
0,275
|
0,500
|
Подобные зависимости были получены и для расчета активных зон реактора ВВЭР. Например в [9] предложена зависимость
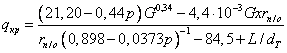 ,
(9)
,
(9)
где
![]() —
давление,
—
давление, ![]() —
массовое
паросодержание,
—
массовое
паросодержание,
![]() —
массовая
скорость,
—
массовая
скорость, ![]() —
длина пучка,
—
длина пучка, ![]() —
тепловой
диаметр
сборки,
—
тепловой
диаметр
сборки, ![]() —
площадь
сечения
сборки;
—
площадь
сечения
сборки; ![]() —
обогреваемый
периметр
сечения
сборки. Как и все
эмпирические
зависимости,
зависимость
(9) применима
только в
определенном
диапазоне
значений
входящих в
нее
параметров, представленных
в таблице 2.
—
обогреваемый
периметр
сечения
сборки. Как и все
эмпирические
зависимости,
зависимость
(9) применима
только в
определенном
диапазоне
значений
входящих в
нее
параметров, представленных
в таблице 2.
Таблица 2. Диапазоны изменения параметров в соотношении (9).
|
|
|
|
|
|
|
10,3 — 18, 6
|
530 — 3230
|
- 0,07— 0,4
|
9
|
1— 3,5
|
В расчетах ОАО ОКБ «Гидропресс» применяется соотношение, предложенное Ю.А. Безруковым, и приведенное в [9]
![]() ,
(10)
,
(10)
где
![]() ,
, ![]() .
.
Таблица 3. Диапазоны изменения параметров в формуле (10)
|
|
|
|
|
|
|
7,45—16,7
|
700 —3800
|
- 0,07— 0,4
|
9
|
1,7—3,5
|
В результате экспериментов по определению кризиса кипения в различных конструкциях были накоплены данные для широкого диапазона изменения параметров, а с вводом соответствующих поправок удается получить величины критического потока для любых вариантов этих параметров. Данная работа велась в 70-х гг. прошлого века в США. В настоящее время такие же работы проводятся в России. Недавно опубликован табличный метод, представляющий собой массивы (таблицы) экспериментальных данных для сборок из базы данных ФЭИ [12]. Эти массивы характеризуются следующими параметрами:
· число экспериментальных точек 963;
·
диаметр
твэлов ![]() от
10,2 до 15 мм;
от
10,2 до 15 мм;
·
относительный
шаг ![]() от
1,15 до 1,88;
от
1,15 до 1,88;
· число твэлов в сборках 4, 9, 16 и 20;
· геометрия сечения обечайки — прямоугольник;
·
относительная
длина сборки
(отношение длины
пучка твэлов ![]() к
тепловому
диаметру
к
тепловому
диаметру ![]() )
40—960;
)
40—960;
· все твэлы обогреваемые;
· обогрев равномерный по длине и сечению;
·
диапазон
давления ![]() =4 —
15,6 МПа;
=4 —
15,6 МПа;
·
диапазон
массовой скорости
![]() =115—
4810 кг/(м2с);
=115—
4810 кг/(м2с);
·
диапазон
паросодержания
от ![]() = - 0,17
до 0,87.
= - 0,17
до 0,87.
Опубликованные
в [12] таблицы
содержат
значение
критического
теплового
потока ![]() ,
для которого
,
для которого
·
тепловой
диаметр
регулярной
ячейки ![]() ;
;
·
относительный
шаг ![]() ;
;
·
относительное
расстояние
от места
кризиса до
входа в сборку
![]() ;
;
·
коэффициент
гидравлического
сопротивления
дистанционирующих
решеток ![]() ;
;
·
расстояние
от места
кризиса до ближайшей
дистанционирующей
решетки ![]() ;
;
·
отношение
максимального
теплового
потока к среднему
по сечению ![]() .
.
Для расчета критического теплового потока по табличному методу ФЭИ при равномерном по длине энерговыделения используется соотношение
![]() .
(11)
.
(11)
В соотношении (11)
·
![]() —
поправочная
функция на
тепловой
диаметр
ячейки;
—
поправочная
функция на
тепловой
диаметр
ячейки;
·
![]() —
поправочная
функция на
относительный
шаг;
—
поправочная
функция на
относительный
шаг;
·
![]() —
поправочная
функция на
относительное
расстояние от
места кризиса
до входа в
сборку;
—
поправочная
функция на
относительное
расстояние от
места кризиса
до входа в
сборку;
·
![]() —
поправочная
функция,
учитывающая
влияние
дистанционирующей
решетки
(переменная
—
поправочная
функция,
учитывающая
влияние
дистанционирующей
решетки
(переменная ![]() );
);
·
![]() —
поправочная
функция на
теплогидравлическую
неравноценность
сборки,
равная
единице в
случае одинаковых
ячеек;
—
поправочная
функция на
теплогидравлическую
неравноценность
сборки,
равная
единице в
случае одинаковых
ячеек;
·
![]() —
поправочная
функция на
неравномерность
энерговыделения
по сечению
сборки;
—
поправочная
функция на
неравномерность
энерговыделения
по сечению
сборки;
Поправочная
функция ![]() сформирована
и
оптимизирована
авторами [12]
на
экспериментальных
данных, полученных
при
неравномерном
по сечению
сборки
энерговыделении.
Она
учитывает предельный
переход от
неравномерного
к равномерному
по сечению
энерговыделению.
сформирована
и
оптимизирована
авторами [12]
на
экспериментальных
данных, полученных
при
неравномерном
по сечению
сборки
энерговыделении.
Она
учитывает предельный
переход от
неравномерного
к равномерному
по сечению
энерговыделению.
3. Анализ путей повышения величины критического теплового потока с использованием табличного метода ФЭИ.
Повышение
мощности
активной
зоны требует
повышения
величины
критического
теплового
потока.
Конструкции
ТВС активных
зон
отечественных
и зарубежных водо-водяных
реакторов
имеют
определенные
размеры
твэлов, шаг
их
расположения,
тепловые
диаметры
ячеек,
однозначно
определяя
величины ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() из
зависимости
(11). Единственной
возможностью
повышения
величины
критического
теплового
потока
остается
варьирование
параметрами
функции
из
зависимости
(11). Единственной
возможностью
повышения
величины
критического
теплового
потока
остается
варьирование
параметрами
функции ![]() —
шагом
расположения
решеток и
коэффициентом
гидравлического
сопротивления.
—
шагом
расположения
решеток и
коэффициентом
гидравлического
сопротивления.
Например,
для
квадратной
ячейки ТВС,
типичной для
реактора PWR (рис.
4), средний
равномерный
тепловой
поток с
поверхности
твэлов ![]() . Допускается
наличие
максимально
напряженной
ячейки с
равномерным
по высоте
тепловым
потоком (ТП)
. Допускается
наличие
максимально
напряженной
ячейки с
равномерным
по высоте
тепловым
потоком (ТП) ![]() .
При
повышении
тепловой
мощности
активной
зоны на 30%,
тепловой
поток в
рассматриваемой
ячейке
станет равен
.
При
повышении
тепловой
мощности
активной
зоны на 30%,
тепловой
поток в
рассматриваемой
ячейке
станет равен ![]() .
Массовая
скорость
.
Массовая
скорость ![]() не
меняется.
Тогда при
наличии
только обычных
дистанционирующих
решеток,
расположенных
с шагом 500 мм и
имеющих
не
меняется.
Тогда при
наличии
только обычных
дистанционирующих
решеток,
расположенных
с шагом 500 мм и
имеющих ![]() ,
наблюдается
кризис
кипения на
расстоянии 3480
мм от низа
активной
зоны.
,
наблюдается
кризис
кипения на
расстоянии 3480
мм от низа
активной
зоны.
Рис. 4 . Квадратная ячейка PWR
Возможны два варианта повышения величины КТП по всей высоте активной зоны:
1. Варьирование шагом решеток.
Уменьшение шага решеток приведет к увеличению числа решеток в активной зоне, что, во-первых, приведет к росту потерь давления, а во-вторых, окажет влияние на нейтронно-физические характеристики активной зоны за счет увеличения количества металла в ней, являющимся паразитным поглотителем нейтронов.
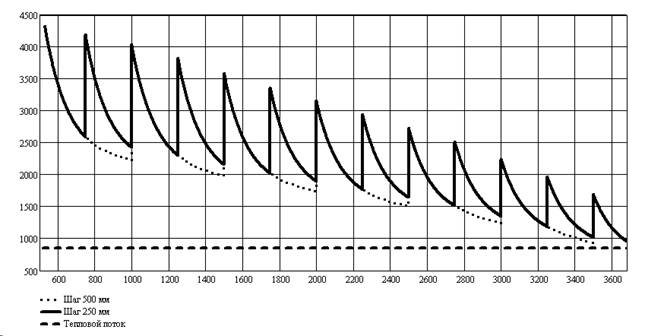
Рис. 5 . График зависимости КТП от шага расположения решеток
Уменьшение
шага с 500 мм до 250
мм (рис.5) при ![]() позволяет
поднять КТП
на 9% по
сравнению с первоначальным
вариантом
расположения
решеток. Но
при этом в 2
раза
увеличилось
количество
решеток, а,
следовательно,
и потери давления
от действия
всех решеток
возрастут в
те же 2 раза.
позволяет
поднять КТП
на 9% по
сравнению с первоначальным
вариантом
расположения
решеток. Но
при этом в 2
раза
увеличилось
количество
решеток, а,
следовательно,
и потери давления
от действия
всех решеток
возрастут в
те же 2 раза.
2. Варьирование коэффициентом гидравлического сопротивления.
В этом случае количество решеток не меняется, не увеличивается доля металла в активной зоне, но меняется величина гидравлических потерь.
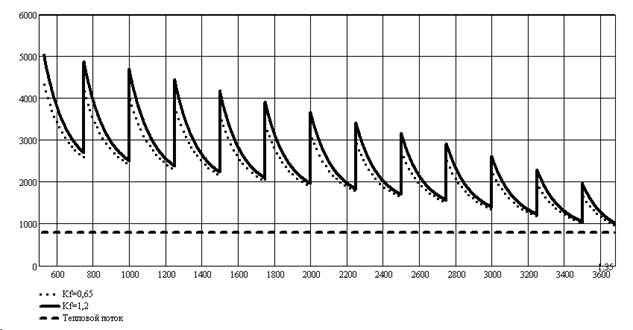
Рис. 6 .
График
зависимости
КТП от
коэффициента
гидравлического
сопротивления
![]()
Увеличение ![]() с
0,65 до 1,2 при шаге 250
мм (рис.6)
позволяет
поднять КТП
еще на 3,4% по
отношению к
варианту с
шагом
расположения
250 мм и
с
0,65 до 1,2 при шаге 250
мм (рис.6)
позволяет
поднять КТП
еще на 3,4% по
отношению к
варианту с
шагом
расположения
250 мм и ![]() .
Хотя
количество
решеток в
этом случае
не увеличивается,
но
возрастает
их гидравлическое
сопротивление,
а,
следовательно,
и гидравлическое
сопротивление
активной
зоны.
.
Хотя
количество
решеток в
этом случае
не увеличивается,
но
возрастает
их гидравлическое
сопротивление,
а,
следовательно,
и гидравлическое
сопротивление
активной
зоны.
Заключение.
Одним из ограничений увеличения мощности как работающих, так и проектируемых ТВС служит кризис теплообмена. Кризис теплообмена в пучке ТВС имеет локальный характер и в настоящее время рассчитывается по моделям, обобщающим экспериментальные данные, полученные на электрообогреваемых имитаторах ТВС, учитывающих особенности конкретных пучков твэлов. Но как правильно заметили авторы [12], в ряде случаев полученные результаты стоит рассматривать как оценочные и нуждающиеся в подтверждении экспериментом. Тем не менее, было установлено, что дистанционирующие, перемешивающие решетки позволяют существенно увеличить значение критического теплового потока. Выбором положения решетки, их характеристик и количества можно повысить тепловую мощность ТВС принятых для ВВЭР-1000 размеров на 15-20%.
Список используемой литературы.
1. Драгунов Ю.Г., Рыжов С.Б., Васильченко И.Н., Кобелев С.Н., Вьялицын В.В. Проект активной зоны для РУ АЭС-2006. Материалы конференции: Обеспечение безопасности АЭС с ВВЭР. ФГУП ОКБ ГИДРОПРЕСС, 2007.
2. Асмолов В.Г. Атомная энергетика – второе рождение. Научный совет РНЦ «Курчатовский институт», М, 2007.
3. Петухов Б.С., Генин Л.Г., Ковалев С.А., Соловьев С.Л. Теплообмен в ядерных энергетических установках. М., Изд-во МЭИ, 2003. 548с.
4. Тонг Л. Теплоотдача при кипении и двухфазное течение. М., «Мир», 1960. 280с.
5. Осмачкин В. С. Кризис теплообмена при движении кипящей воды вдоль пучков тепловыделяющих стержней. Препринт ИАЭ — 2014. М., 1970.
6. Смолин В. Н. Модель механизма кризиса теплоотдачи при движении пароводяной смеси и методика расчета кризисных условий в трубчатых твэлах.— В кн.: Исследование критических тепловых потоков в пучках стержней. Семинар СЭВ ТФ—74. М., 1974, с. 209—224.
7. Смолин В. Н., Поляков В. К. Критический тепловой поток при продольном обтекании пучка стержней. — Теплоэнергетика, 1967, ╧ 4, с., 54-58.
8. Дубровский И. С., Югай Т., Пащенко М. П., Чалых А. Ф. Кризис теплообмена при вынужденном течении пароводяной смеси в сборке стержней в стационарных и нестационарных режимах. В кн.: Исследование критических тепловых потоков в пучках стержней. Семинар СЭВ ТФ—74. М., 1974, с. 67—78.
9. Безруков Ю. А., Астахов В. И., Салий Л. А. и др. Исследование критических тепловых потоков в пучках стержней применительно к реакторам ВВЭР. В кн.: Семинар СЭВ ТФ—74. Исследование критических тепловых потоков в пучках стержней. М., 1974, с. 57—66.
10. Емельянов И.Я., Солонин В. И., Михан В.И., Рекшня Н.Ф., Конструирование ядерных реакторов. М. Энергомиздат.1982.
11. Кириллов П.Л. Справочник по теплогидравлическим расчетам (ядерные реакторы, теплообменники, парогенераторы). М. Энергоатомиздат. 1984.
12. Бобков В.П., Ефанов А.Д. и др. Таблица для критических тепловых потоков в сборках твэлов в квадратной упаковке. М. Атомная энергия: том 98, вып.1: 2005.
Публикации
с ключевыми
словами: активная
зона
ядерного
реактора, реактор
с водой под
давлением, кризис
кипения, критический
тепловой
поток Публикации
со словами: активная
зона
ядерного
реактора, реактор
с водой под
давлением, кризис
кипения, критический
тепловой
поток
Тематические рубрики:
Публикации с ключевыми словами: активная зона ядерного реактора, реактор с водой под давлением, кризис кипения, критический тепловой поток
Публикации со словами: активная зона ядерного реактора, реактор с водой под давлением, кризис кипения, критический тепловой поток
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



