научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 04, апрель 2009
УДК 532.5
Россия, Москва, МГТУ им. Н.Э. Баумана,
ФГУП «Центр Келдыша»
ilmovdn@rambler.ru,
kaskov@power.bmstu.ru
Работа посвящена исследованию процесса генерации мощных акустических волн путем высоковольтного импульсного электрического разряда в жидкой среде. Благодаря возможности формирования импульсов давления высокой амплитуды, этот метод позволяет воздействовать на некоторые характеристики среды, такие как состав, вязкость, дисперсность. Рассматривается возможность улучшения характеристик нефтепродуктов, в частности, топочного мазута.
При воздействии импульсов давления высокой амплитуды, обрабатываемая среда подвергается воздействию сжимающих и растягивающих нагрузок. В результате – возможно дробление частиц дисперсной фазы многокомпонентных нефтепродуктов и крекинг многоатомных углеводородных молекул. Предполагаются следующие механизмы этих явлений:
1. Разрыв частиц и молекул на резком фронте ударной волны.
2. Кавитация в зонах разряжения, возникающих за волнами сжатия с последующим схлопыванием пузырьков отраженными от границ волнами сжатия.
Особенности распространения ударных волн в сжимаемой жидкости определяют условия реализации указанных процессов.
Сформулируем необходимые условия, позволяющие моделировать ударные волны в жидкой среде. Рассматривается однокомпонентная сплошная упругая среда. Пусть ею будет вода, которой заполнен разрядный узел установки. Механические свойства воды и тяжелых нефтепродуктов близки, а акустическая жесткость резиновой мембраны такова, что волны из разрядного узла переходят в камеру с обрабатываемой жидкостью практически без искажений. В качестве уравнения состояния жидкости использовано эмпирическое уравнение Тэта [1]:
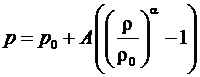 (1)
(1)
Здесь ![]() - давление,
- давление, ![]() - плотность;
- плотность; ![]() - некоторые начальные значения принятые
- некоторые начальные значения принятые ![]() Па,
Па, ![]() кг/м3;
кг/м3; ![]() - постоянные величины, которым заданы значения
- постоянные величины, которым заданы значения ![]() Па,
Па, ![]() . Данное уравнение выполняется в умеренном диапазоне температур рабочего процесса установки. Скорость звука в жидкости (1) будет определяться формулой:
. Данное уравнение выполняется в умеренном диапазоне температур рабочего процесса установки. Скорость звука в жидкости (1) будет определяться формулой:
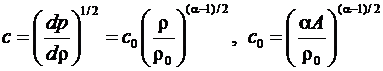 (2)
(2)
Здесь ![]() - скорость звука при
- скорость звука при ![]() .
.
Геометрия установки позволяет выбрать цилиндрическую систему координат. Тогда уравнение неразрывности принимает вид:
 (3)
(3)
где ![]() - текущее время,
- текущее время, ![]() и
и ![]() - радиальная и поперечная координаты,
- радиальная и поперечная координаты, ![]() и
и ![]() – радиальная и поперечная компоненты скорости.
– радиальная и поперечная компоненты скорости.
Жидкость будет считаться невязкой. Данное предположение позволит избавиться от вычислительных погрешностей, связанных с апроксимацией вязких членов, и получить идеализированные условия без диссипации механической энергии. Выполнение энергетического баланса, также как баланса массы, послужит критерием точности численного решения. Итак, уравнение движения невязкой жидкости в проекциях на оси цилиндрической системы координат:
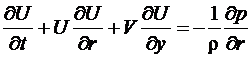 (4)
(4)
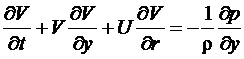 (5)
(5)
Уравнения (3-5) апроксимируются явной разностной схемой первого порядка точности по времени, являющейся модификацией схемы Лакса [2], на двумерную пространственную сетку (рис. 1) по следующему шаблону.

Рис. 1. Пространственная сетка.


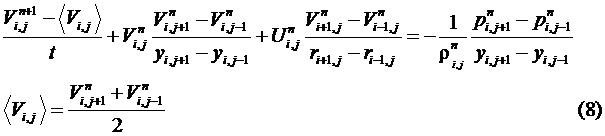
Верхние индексы n и n+1 соответствуют текущему и следующему временному шагу.
Использование данной простой схемы обеспечивает сквозной расчет без выделения фронта ударной волны. Однако наличие схемной вязкости вызывает размазывание фронта волны и убыль энергии системы. Для уменьшения этих эффектов требуется достаточно подробная пространственная сетка. Сравнение решения по выбранной схеме с решением по схеме Мак-Кормака [2], которое имеет второй порядок точности по времени и обладает погрешностью не диссипативного, а дисперсионного характера, показало целесообразность выбранного метода.
Приведенный математический алгоритм реализован на модели действующей экспериментальной установки (рис. 2). Она представляет собой емкость заполненную обрабатываемой жидостью, которая подвергается ударно-волновому воздействию. Ударные волны инициируются электрическим разрядом, происходящим между электродами в разрядном узле.

Рис. 2. Схема электроимпульсной установки.
Геометрические параметры установки приведены на рис. 3.1. На нем изображена расчетная область ограниченная условиями симметрии. Пространственный шаг расчетной сетки по радиусу и поперечной координате ![]() мм. Уклоны и криволинейные поверхности электродов на сетке моделируются «ступеньками». Шаг по времени переменный, задается согласно условию Куранта:
мм. Уклоны и криволинейные поверхности электродов на сетке моделируются «ступеньками». Шаг по времени переменный, задается согласно условию Куранта:
 (9)
(9)
Для моделирования электрического разряда, инициирующего ударную волну в сплошной среде используется следующий прием. В начальный момент времени в межэлектродном пространстве находится область сжатой жидкости до давления 165 кбар (рис. 3.1). Работа, необходимая для сжатия данного объема жидкости равна энергии электрического разряда (1000 Дж). Поля давления, полученные при моделировании распространения волн показаны на рис. 3.2-3.6. В точках экспериментальной установки, отмеченных на рис. 2, имеются датчики давления. Наибольшие значения давлений, полученные при численном решении в данных точках приведены на рис. 3.3, 3.4, 3.6. Важно, что они удовлетворительно совпадают с экспериментом.
|
|
|
|
|
|
|
|
Рис. 3.1-3.6. Начальные условия и результаты моделирования. Поля давления в различные моменты времени после импульсного разряда.
Профили давления в радиальном сечении установки приведены на рис. 4. Огибающая показывает амплитуду давления волны сжатия по мере ее движения по радиусу. Так до прохождения волны сквозь мембрану, давление в ней уменьшается в тысячи раз и составляет около 350 бар, а при достижении границы камеры давление в прямой волне уменьшается до 100 бар. Здесь происходит отражение волн сжатия, влияет также эффект вызванный наклонными стенками, вследствие чего наибольшее давление на дальней от электродов стенки камеры при отражении волн достигает 280 бар. Вслед за волной сжатия идет волна разряжения. В упругой среде ее амплитуда сравнима с амплитудой волны сжатия. В реальной жидкости растягивающие напряжения приводят к разрыву сплошности и образованию кавитации. На рис. 4 нереализующиеся части профилей отрицательного давления показаны штриховой линией.

Рис. 4. Профили волны сжатия в радиальном сечении установки.
Обратимся к энергетике происходящих процессов. Энергия рассматриваемой среды состоит из двух составляющих. Одна из них это кинетическая энергия движения, вторую назовем потенциальной энергией сжатия. Удельная объемная кинетическая энергия среды выражается формулой
 (10)
(10)
Удельная потенциальная энергия среды равна работе, отнесенной к единице объема, затраченной на сжатие среды от плотности ![]() до
до ![]() или от давления
или от давления ![]() до
до ![]() .
.
 (10)
(10)
 (11)
(11)
или  (12)
(12)
Отметим, что при ![]() удельную потенциальную энергию можно оценить по
удельную потенциальную энергию можно оценить по
 (13)
(13)
Кинетическая, потенциальная и полная механическая энергия системы вычисляются как
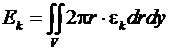 (14)
(14)
 (15)
(15)
![]() (16)
(16)
На рис. 5 приведен график изменения потенциальной и кинетической энергии системы, полученный по результатам моделирования. Видно, как потенциальная энергия сжатой жидкости в начале процесса переходит в кинетическую энергию волны, а затем устанавливается колебательный процесс.
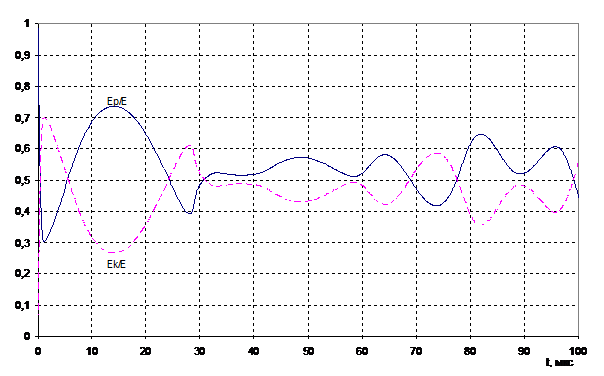
Рис. 5. Изменение потенциальной и кинетической энергии в упругой среде.
На рис. 6 показана механическая энергия, поступившая в камеру с обрабатываемой жидкостью, отнесенная к полной энергии системы ![]() . Время прохождения первой волны сжатия до стенки вдоль радиуса установки занимает около 100 мкс. За это время в камере обработки за мембраной сосредотачивается около 50% энергии системы (разряда). При равномерном распределении энергии в жидкости, внутри этой камеры находилось бы около 56%, что равно отношению объема камеры к объему всей установки. Отметим, что с первой волной сжатия в камеру проникает около 20% энергии разряда (
. Время прохождения первой волны сжатия до стенки вдоль радиуса установки занимает около 100 мкс. За это время в камере обработки за мембраной сосредотачивается около 50% энергии системы (разряда). При равномерном распределении энергии в жидкости, внутри этой камеры находилось бы около 56%, что равно отношению объема камеры к объему всей установки. Отметим, что с первой волной сжатия в камеру проникает около 20% энергии разряда (![]() ).
).
На рис 6 также приведен относительный объем камеры с отрицательным давлением (![]() ). Полный объем камеры
). Полный объем камеры ![]() л. График показывает, что кавитация может происходить в объеме занимающем до 50% от
л. График показывает, что кавитация может происходить в объеме занимающем до 50% от ![]() . При последующем схлопывании кавитационных пузырей в условиях экстремальных температур и давлений, которые могут сопровождать этот процесс, возможен крекинг нефтепродуктов.
. При последующем схлопывании кавитационных пузырей в условиях экстремальных температур и давлений, которые могут сопровождать этот процесс, возможен крекинг нефтепродуктов.

Рис. 6. Поступление механической энергии в камеру с обрабатываемой жидкостью и относительный объем кавитационной области.
В заключение оценим энергию, необходимую для диссоциации молекул нефтепродуктов с высокой молекулярной массой. Найдем характерное значение удельной энергии диссоциации в расчете на единицу массы сырья. Известно, что энергия связей органических молекул составляет величину порядка ![]() кДж/моль [3]. Энергия распада слабо-связанных надмолекулярных структур может составлять величину 50-150 кДж/моль. Полагая характерную молекулярную массу
кДж/моль [3]. Энергия распада слабо-связанных надмолекулярных структур может составлять величину 50-150 кДж/моль. Полагая характерную молекулярную массу ![]() г/моль, получим значение удельной массовой энергии диссоциации
г/моль, получим значение удельной массовой энергии диссоциации ![]() МДж/кг. Будем считать энергией одного разряда попадающей в камеру с обрабатываемой жидкостью величину
МДж/кг. Будем считать энергией одного разряда попадающей в камеру с обрабатываемой жидкостью величину ![]() Дж. Этой энергии достаточно на однократное разрушение массы углеводородного сырья равной
Дж. Этой энергии достаточно на однократное разрушение массы углеводородного сырья равной ![]() г. Полагая, что энерговклад каждого импульса полностью идет на химическое превращение, учитывая объем камеры (
г. Полагая, что энерговклад каждого импульса полностью идет на химическое превращение, учитывая объем камеры (![]() л) и плотность топочного мазута (
л) и плотность топочного мазута (![]() кг/м3), можно получить, что энергии 100 импульсов может быть достаточно для образования 4% светлых фракций.
кг/м3), можно получить, что энергии 100 импульсов может быть достаточно для образования 4% светлых фракций.
Выявлены основные качественные особенности распространения ударных волн, наглядно иллюстрирующие процесс. Получены оценки параметров среды для предварительного расчета поведения кавитационных пузырьков и возможности протекания в них реакций. Оценен объем кавитационной области и достижимый энерговклад в среду, который может быть сопоставим с удельной энергией термического крекинга типичных углеводородов.
Работа выполнена в рамках госконтракта от 4 августа 2008г ╧ 02.516.12.6010 и при поддержке РФФИ (грант 08-08-00203-а).
Литература
1. Зельдович Я.Б., Райзер Ю.П. Физика ударных волн и высокотемпературных гидродинамических явлений. М.: «Наука», 1966г, 688 с.
2. Д. Андерсон, Дж. Таннехилл, Р. Плетчер. Вычислительная гидромеханика и теплообмен. Ч. 1. М.: «Мир», 1990, 384 с.
3. Бухаркина Т.В., Дигунов Н.Г. Химия природных энергоносителей и углеродных материалов. М.: Изд. РХТУ, 1998г.
Публикации с ключевыми словами: электроимпульсная установка, нефтепереработка
Публикации со словами: электроимпульсная установка, нефтепереработка
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||









