научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 04, апрель 2009
УДК 621.436:519.673
Введение.
В последние 2-3 десятилетия развитие поршневых двигателей внутреннего сгорания (ДВС), характеризующееся непрерывным совершенствованием их конструкции и повышением показателей, следует оценивать как ускоренное, что обусловлено использованием достижений высоких технологий в различных отраслях, связанных с двигателестроением (электронное управление, механотроника, триботехника, химмотология, материаловедение, технология обработки и др). Существенное воздействие на совершенствование основных показателей ДВС, прежде всего экологических и экономических, оказали национальные законодательные стандарты как действующие, так и намечаемые на близкую и отдаленную перспективы. Все это в итоге привело к необходимости качественного ускорения проектирования и освоения в производстве новых двигателей. Сегодняшние рекордные сроки в 12 месяцев от получения технического задания на проектирование до начала серийного выпуска нового двигателя 10-15 лет назад вообще нельзя было представить возможными. Однако это осуществлено и определяющая роль, наряду с другими факторами, здесь принадлежит современным методам математического моделирования и расчетов циклов (процессов) ДВС и соответственно нагрузок, действующих на основные детали. В конечном итоге задача состоит в том, чтобы на стадии проектирования, т.е. до изготовления реального образца ДВС, можно было бы быстро и достоверно прогнозировать показатели вновь создаваемого двигателя.
Необходимо отметить, что огромную роль математическое моделирование играет и после создания двигателя: при его испытаниях. В процессе проектирования двигателя, проведении испытаний, подготовки к серийному производству компании-производители борются за снижение средств и времени, потраченных на выполнение работ. В условиях рыночной экономики это становится одним из определяющих факторов. Стоимость одного часа испытаний на стенде, оборудованном двигателем, намного больше стоимости испытаний, проведенных с помощью компьютера. Поэтому компани-автопроизводители на предварительных испытаниях используют математическое моделирование.
1. Постановка задачи.
Наиболее жесткие требования по экологии, экономичности, удельной мощности предъявляются к автомобильным ДВС. Достижение высоких экологических, экономических , мощностных показателей, обеспечивается, в том числе, и точным управлением рабочим процессом, которое осуществляется микропроцессорным электронным блоком управления (ЭБУ). Современный ЭБУ выполнят большое количество различных функций, каждую из которых необходимо протестировать при проектировании ЭБУ, когда двигатель находится еще в стадии разработки. Процесс тестирования производится в режиме полунатурного моделирования, когда реальный ЭБУ сопрягается с компьютерной математической моделью ДВС, имитирующей динамические режимы работы двигателя с максимально возможной точностью и высоким быстродействием.
Тестировочный стенд включает в себя (Рис. 1):
- персональный компьютер для запуска, проведения, обработки и иллюстрации результатов теста;
- ЭБУ как объект тестирования;
- симулятор – устройство, обеспечивающее расчет модели, генерацию сигналов связи между натурной и модельной частями стенда: широтно-импульсной модуляции (ШИМ), аналоговых, цифровых.
При необходимости стенд комплектуют дополнительным оборудованием:
- блоком прерывания сигналов для возможности их анализа;
- осцилогрофом для наблюдения сигналов.

Рис. 1. Тестировочный стенд.
В практике разработки и исследования двигателей инженеры обычно имеют дело с двумя основными типами математических моделей:
- моделями, построенными на основе описания физико-химических процессов, протекающих в двигателе и его элементах, такие модели базируются на основных законах сохранения массы, энергии и количества движения [1, 2];
- эмририческими, или, как их часто называют, статистическими моделями, полученными на основании эксперименов, выполненных на натурном объекте, а иногда и на основании расчетных экспериментов на моделях первого типа.
Эмпирические модели, как правило, не отражают сущности реальных физико-химических процессов, происходящих в двигателе, и не используются для их анализа, но такие модели позволяют прогнозировать поведение объекта при изменении независимых переменных и с успехом применяются при решении ряда практических задач [2].
Модель, представленная в данной работе, предназначена для тестирования ЭБУ и включает как эмпирическую часть, так и часть, которая рассчитывается на основе описания физико-химических процессов. Обмен сигналами между натурной и модельной частями стенда осуществляется в реальном времени, поэтому одним из основных критериев является время, необходимое для расчета в модели одной рабочей точки. Обмен данными в системе ЭБУ – модель ДВС просходит за 1 мс. Это означает, что необходимо произвести расчет всех функций за этот период. Расчет рабочей точки программными продуктами такими как Star-Cd [3], AVL Fire [4] и т.д., основанными на 3-D моделях, описывающих только физико-химические процессы, произвести за 1 мс невозможно. Данные модели рассчитывают определенный рабочий режим за 2-3 дня, что неприемлемо для задач симулирования двигателя в режиме реального времени. С другой стороны, для задачи тестирования функций ЭБУ нет необходимости моделировать работу двигателя с большой точностью. Для достижения цели достаточно получить модель с 10 процентной погрешностью.
Таким образом, возникает задача разработки математической модели ДВС, удовлетворяющей следующим требованиям:
- время расчета рабочей точки должно составлять 1 мс;
- допустимая погрешность модели должна быть не более 10 %;
- расчет рабочего процесса в модели должен осуществляться как отклик на сигналы, вырабатываемые ЭБУ и посылаемые на исполнительные механизмы.
2. Принципиальная схема дизеля.
При создании модели автомобильный дизель представлен в виде совокупности следующих основных элементов (рис. 2): поршневая часть (ПЧ); впускной трубопровод (ВпТ); выпускной трубопровод (ВыпТ); турбина (Т) и компрессор (К), входящие в состав турбокомпрессора (ТКР); механизм переменной геометрии турбины (МПГТ); теплообменник для охлаждения наддувочного воздуха (ТНВ); теплообменник для охлаждения газа в системе рециркуляции отработавших газов (ТРГ); клапан рециркуляции отработавших газов (КР).

Рис. 2. Принципиальная схема автомобильного дизеля.
3. Математическая модель. Основные уравнения.
Ниже приведены основные уравнения и принципы построения математической модели автомобильного дизеля, работающей в режиме реального времени.
При расчёте впускного и выпускного трубопроводов объёмы трубопроводов V рассматривались для впускного – от компрессора до впускных клапанов, для выпускного – от выпускных клапанов до турбины. Приняты допущения: нет потерь на трение и теплоотдачи от газа в стенки трубопровода; давление и температура газа одинаковы во всём трубопроводе; газ рассматривался как идеальный.
Использовались следующие уравнения.
1) Уравнение сохранения массы:
![]() (1),
(1),
где t – время; ![]() – масса газа в объеме V,
– масса газа в объеме V, ![]() – масса i-ого газа, втекающего в объём V,
– масса i-ого газа, втекающего в объём V, ![]() – масса j-ого газа, вытекающего из объёма V.
– масса j-ого газа, вытекающего из объёма V.
2) Уравнение сохранения энергии:
![]() (2),
(2),
где Uсм – внутренняя энергии газа в объёме V; Q – теплота, переданная в теплообменник; H – сумма энтальпий втекающих и вытекающих потоков газа.
Запишем выражения для каждого члена уравнения (2).
Для первого члена
a)  (3);
(3);
где ![]() – теплоемкость газа при постоянном объёме;
– теплоемкость газа при постоянном объёме; ![]() – температура газа в объёме V.
– температура газа в объёме V.
Для второго члена
б) ![]() (4),
(4),
где ![]() – температура газов перед теплообменником;
– температура газов перед теплообменником; ![]() - температура атмосферного воздуха;
- температура атмосферного воздуха; ![]() - расход газа через теплообменник.
- расход газа через теплообменник.
Для третьего члена
в) ![]() (5),
(5),
где ![]() и
и ![]() - теплоемкости при постоянном давлении втекающих и вытекающих газов соответственно;
- теплоемкости при постоянном давлении втекающих и вытекающих газов соответственно; ![]() и
и ![]() - массы втекающих и вытекающих газов соответственно;
- массы втекающих и вытекающих газов соответственно; ![]() и
и ![]() - температуры втекающих и вытекающих газов соответственно.
- температуры втекающих и вытекающих газов соответственно.
3) Уравнение состояния идеального газа Менделеева-Клапейрона:
![]() (6),
(6),
где ![]() - давление газа в объеме V,
- давление газа в объеме V, ![]() - газовая постоянная.
- газовая постоянная.
Теплоемкости при постоянном давлении задавались как функции температуры
![]() (7-9).
(7-9).
Расход газовоздушной смеси истекающей из объема впускного трубопровода
 (10).
(10).
Расход газовоздушной смеси втекающей в объем выпускного трубопровода
 (11),
(11),
где ![]() - частота вращения коленчатого вала,
- частота вращения коленчатого вала, ![]() - рабочий объём цилиндра,
- рабочий объём цилиндра, ![]() - количество цилиндров,
- количество цилиндров, ![]() - плотность смеси в объёме V,
- плотность смеси в объёме V, ![]() - коэффициент наполнения,
- коэффициент наполнения, ![]() - расход топлива. Расходы
- расход топлива. Расходы ![]() и
и ![]() рассчитывается в модели ТКР. Решая систему уравнений (1-11), находим
рассчитывается в модели ТКР. Решая систему уравнений (1-11), находим ![]() и
и ![]() .
.
4. Математическая модель Турбокомпрессора (ТКР)
В процессе разработки модели ТКР необходимо было решить существующие проблемы:
· отсутствие необходимой информации о конструкционных параметрах;
· экспериментальные данные о расходных характеристиках ТКР были получены не для всех режимов работы ДВС;
· время расчета одной рабочей точки не более 1 мс.
Решением стало использования полиномов, экстраполирующих экспериментальные данные расходных характеристик ТКР. В результате использования полиномов были получены следующие расходные характеристики ТКР: G’k(πk,ω’ k), G’t(πt,МПГТ), ηt(πt,ω’t, МПГТ), η’k(πk,ω’ k),
где ![]() - приведенный расход воздуха через компрессор;
- приведенный расход воздуха через компрессор; ![]() - степень повышения давления в копрессоре; ω’k - приведенная частота вращения вала ТКР для расчета компрессора;
- степень повышения давления в копрессоре; ω’k - приведенная частота вращения вала ТКР для расчета компрессора; ![]() - адиабатный КПД компрессора;
- адиабатный КПД компрессора; ![]() - приведенный расход газа через турбину;
- приведенный расход газа через турбину; ![]() - степень понижения давления на турбине; МПГТ - сигнал на механизм управления переменной геометрией турбины; ω’t - приведенная частота вращения вала турбокомпрессора для расчета турбины;
- степень понижения давления на турбине; МПГТ - сигнал на механизм управления переменной геометрией турбины; ω’t - приведенная частота вращения вала турбокомпрессора для расчета турбины; ![]() - адиабатный КПД турбины.
- адиабатный КПД турбины.
 Приведенная частота вращения вала турбокомпрессора для расчета турбины
Приведенная частота вращения вала турбокомпрессора для расчета турбины
,
где Tref – константа температуры, которая задается при получении экспериментальных расходных характеристик ТКР; T3t – температура газов перед турбиной, ωТК – частота вращения вала турбокомпрессора.
 Приведенная частота вращения вала ТКР для расчета компрессора
Приведенная частота вращения вала ТКР для расчета компрессора
,
где Т0 – температура газов перед компрессотром.
Приведенный расход воздуха через компрессор

где Gk – расход воздуха через компрессор.
Приведенный расход воздуха через турбину

где Gt – расход воздуха через турбину, P3t – давление газов перед турбиной.
Угловая скорость ротора ТКР определялась из уравнения вращения твердого тела:
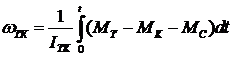 ,
,
где ![]() - момент инерции ротора ТКР;
- момент инерции ротора ТКР; ![]() ,
, ![]() - крутящие моменты турбины и компрессора;
- крутящие моменты турбины и компрессора; ![]() - момент сопротивления, возникающий в результате вращения ротора ТКР.
- момент сопротивления, возникающий в результате вращения ротора ТКР.
Крутящий момент компрессора
 ,
,
где  - расход воздуха через компрессор;
- расход воздуха через компрессор; ![]() - температура воздуха после компрессора,
- температура воздуха после компрессора,
 ,
,
где ![]() - показатель политропы.
- показатель политропы.
Крутящий момент турбины
 ,
,
где  , расход отработавших газов через турбину.
, расход отработавших газов через турбину.
Температура газов после турбины
 .
.
Расчет процессов в цилиндре ДВС производится по методике Гриневецкого – Мазинга описанной в [1].
Заключение.
Предложенная математическая модель автомобильного двигателя, предназначенная для тестирования ЭБУ в режиме реального времени. Соотношения параметров рабочего процесса турбокомпрессора получены в виде полиномов, позволяющих описывать динамические режимы работы в условиях недостаточной информации о характеристиках ТКР.
Модель, описанная выше, реализуется в среде MatLab/Simulink. В MatLab/Simulink встроен компилятор, позволяющий преобразовать модель из формата Simulink в C код, который интегрируется в Симулятор.
Литература
1. Двигатели внутреннего сгорания. В 4 кн. Кн.2. Теория поршневых и комбинированных двигателей. Учеб. по специальности "Двигатели внутреннего сгорания"/ Орлин А.С., Круглов М.Г., Вырубов Д.Н., Иващенко Н.А. и др.; Под ред Орлина А.С., Круглова М.Г. - 4-е издание, переработанное и дополненное. М., Машиностроение, 1983. - 372 с.
2. Луканин В.Н., Морозов К.А. Двигатели Внутреннего сгорания. В 3 кн. Кн. 1. Теория рабочих процессов. М.: Высшая школа. 1995. 368 с.
3. Интернет сайт http://www.cd-adapco.com/products/STAR-CD/index.html
4. Интернет сайт http://www.avl.com/wo/webobsession.servlet.go?app=bcms&page=view&nodeid=400012977 www.avl.com
Публикации с ключевыми словами: моделирование, динамический режим
Публикации со словами: моделирование, динамический режим
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



