научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 03, март 2009
УДК 004.3
+519.6
МГТУ им.
Н.Э.Баумана,
При решении задач структурного синтеза в качестве аппарата формализации объектов проектирования широко применяется теория графов. Использование в качестве формального описания объекта графа определенного вида – обыкновенных неориентированного и ориентированного, гипер- и ультраграфа позволяет получать модели, адекватные в смысле полноты и правильности отображения информации, которая требуется для решения задачи.
Аппарат теории обыкновенных графов глубоко развит, определены операции на графах, сформулированы теоремы, леммы и т. п., разработано много алгоритмов решения различных задач структурного синтеза. Гипер- и особенно ультраграфы исследованы в меньшей степени. Автору не известен единый подход к определению понятий ультра-, гипер- и обыкновенных графов. Все это не позволяет использовать значительные результаты, полученные в теории обыкновенных графов, для решения тех задач структурного синтеза, в которых моделями объектов являются гипер- и ультраграфы. В данной статье автор предлагает такой подход, показывая при этом связь между ультра- гипер- и обыкновенными графами. Приведены формальные правила, связывающие матричное и аналитическое представления для каждого вида графов, а также выражения для оценки характеристик компонент графа.
В соответствии с предлагаемым подходом граф – это два непересекающихся множества X – вершин и U – ребер, на элементах которых задана пара двуместных предикатов-отношений инцидентности Г1 (X, U) и Г2 (U, X). Предикат Г1 (X, U) соответствует такой связи между элементами множеств X и U, которая содержательно определяется выражением – «вершинам множества X инцидентны ребра множества U», а предикат Г2 (U, X) можно записать как «ребрам множества U инцидентны вершины множества X».
Предикаты Г1 (X, U) и Г2 (U, X) таковы, что для всех графов
при X ¹ Æ и U ¹ Æ справедливо:
Г1(xi,uj) = «и» ® ( Г2(uj,xk) = «и» Ú Г2(uj,xi) = «и»). (1)
Положим X = {x1,x2}, U = {u1}. Тогда, изображая вершины кружками, ребра – отрезком дуги или овалом, истинность предиката Г1(xi,uj) – стрелкой, идущей от xi к uj, а истинность предиката Г2(uj, xi) – стрелкой, идущей от uj к xi, получим, если Г1(x1,u1) = «и» и Г2(u1,x1) = «л», геометрическую интерпретацию выражения (1), представленную на рисунке 1,а. При Г1(x1,u1) = «и» и Г2(u1,x1) = «и» геометрическая интерпретация этого выражения показана на рисунке 1,б.

Рисунок 1 – Геометрическая интерпретация выражения (1)
На элементах множеств X и U определены также двуместные предикаты-отношения смежности F1 (X, X) и F2 (U, U). Вершине xi смежна вершина xt, если существует ребро uj, инцидентное вершине xi, такое, что вершина xt инцидентна этому же ребру. Ребру uj смежно ребро uk, если существует вершина xi, инцидентная ребру uj, такая, что ребро uk инцидентно этой же вершине. Таким образом, понятие смежности вторично по отношению к понятию инцидентности.
Предлагаемая трактовка графов допускает существование в них петель и кратных ребер. Вид графа – обыкновенные неориентированный и ориентированный, гипер- и ультраграф – определяется свойствами предикатов инцидентности Г1 и Г2.
Ультраграфы. Определенный выше граф называется ультраграфом HU (X, U, Г1, Г2), если предикаты Г1 (X, U) и Г2 (U, X) обладают следующим свойством
$ uj Î U (|Г1uj| + |Г2uj| ) >2, (2)
т. е. в графе есть хотя бы одно ребро, суммарное количество вершин, которым оно инцидентно и которые инцидентны ему, больше двух.
Если допустить возможность существования в ультраграфе петель, то наличие петли устанавливается условием
$ uj Î U (Г1uj = Г2uj = x i). (3)
На рисунке 2 приведено изображение ультраграфа, у которого X = {x1, x2, x3, x4, x5}, U = {u1, u2, u3 }, причем u3 – петля при вершине x5.

Рисунок 2 – Ультраграф
Для визуального анализа ультраграфа иногда более наглядным будет его изображение в виде двудольного графа (графа Кенига). В этом случае ребра, как и вершины, представляются кружками, а истинность предикатов Г1 и Г2 как и раньше – стрелками. Такое изображение ультраграфа, показанного на рисунке 2, представлено на рисунке 3,а .

Рисунок 3 – Изображение ультраграфа, показанного на рисунке 2, в виде двудольного графа (а) и геометрическая интерпретация предикатов Г2-1 (X, U) и Г1-1 (U, X) этого же ультраграфа (б)
Представление ультраграфа матрицами инцидентности. Полным и достаточно наглядным способом формального задания ультраграфа является его представление через две матрицы инцидентности А1 и A2, где А1 – матрица истинности предиката Г1 (X, U) и А2 – матрица истинности предиката Г2 (U, X).
Матрица инцидентности А1, задающая связь между вершинами и ребрами, – это прямоугольная матрица размером n ´ m, где n = |X|, m = |U|. Элементы этой матрицы определяются по правилу
ì 1 – если Г1(xi,uj) = «и»
a1 i,j = í ,
î 0 – если Г1(xi,uj) = «л»
где i = 1, n; j = 1, m.
Матрица инцидентности А2 задает связь между ребрами и вершинами. Ее строки соответствуют ребрам, а столбцы – вершинам (размер матрицы m ´ n). Элементы матрицы А2 определяются по правилу
ì 1 – если Г2 (uj,xi) = «и»,
a2 j,i = í
î 0 – если Г2 (uj,xi) = «л».
Матрицы А1 и А2 ультраграфа, показанного на рисунке 2, имеют вид:
|
|
|
|
u1
|
u2
|
u3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1
|
1
|
1
|
0
|
|
|
|
|
x1
|
x2
|
x3
|
x4
|
x5
|
|
|
|
|
|
x2
|
0
|
0
|
0
|
|
|
|
u1
|
0
|
1
|
1
|
0
|
0
|
|
|
|
A1
|
=
|
x3
|
0
|
0
|
0
|
,
|
A2
|
=
|
u2
|
0
|
0
|
0
|
1
|
0
|
.
|
|
|
|
|
x4
|
0
|
0
|
0
|
|
|
|
u3
|
0
|
0
|
0
|
0
|
1
|
|
|
|
|
|
x5
|
1
|
0
|
1
|
|
|
|
|
|
|
|
|
|
|
|
Аналитическое представление ультраграфа – образами и прообразами множеств вершин и ребер относительно предикатов Г1 (X, U) и Г2 (U, X). Аналитически ультраграф будет задан полностью, если заданы множества вершин X, ребер U и образы этих множеств относительно предикатов Г1 (X, U) и Г2 (U, X) соответственно. Рассмотрим сначала данный способ представления.
Образом множества X относительно предиката Р(X,Y) является множество подмножеств
РX = {Рxi / xi Î X}, Рxi = {yj Î Y: Рxi (yj) = «и»},
где Рxi – характеристическое подмножество предиката-свойства Рxi(Y), т. е. образ элемента xi Î X относительно этого предиката.
Зафиксировав в Г1 (X, U) некоторую вершину xi Î X, получим предикат-свойство Г1xi (U) – «вершине xi инцидентны ребра множества U», истинность которого задает i-я строка матрицы А1 предиката Г1 (X, U). Таким образом образ вершины xi Î X относительно предиката Г1 (X, U) – это подмножество Ui+ Í U инцидентных ей ребер. Оно является характеристическим множеством Г1xi предиката-свойства Г1xi (U):
Ui+ = Г1xi = {uj Î U : Г1xi (uj) = «и»}, Ui+ Í U .
Множество подмножеств ребер, инцидентных вершинам xi Î X, т. е. образ множества X относительно предиката Г1, будет
Г1X = {Г1xi / xi Î X}.
Подставив в предикат Г2 (U, X) ребро uj, получим предикат-свойство Г2uj (X) – «ребру uj инцидентны вершины множества X», истинность которого задает j-я строка матрицы предиката Г2 (U, X). Образом ребра uj Î U относительно предиката Г2 (U, X) является подмножество Xj+ Í X вершин, инцидентных этому ребру:
Xj+ = Г2uj = {xi Î X : Г2uj (xi) = «и»}, Xj+ Í X .
Образ множества ребер U относительно того же предиката будет задаваться множеством характеристических подмножеств предикатов-свойств Г2uj (X), т. е. строк матрицы А2:
Г2U = { Г2uj / uj Î U}.
Ультраграф данным способом будет задан, если заданы множества вершин X, ребер U и их образы, т. е. множества подмножеств Г1X и Г2U. Ультраграф при данном способе представления будем обозначать как HU (X, U, Г1X, Г2U). Ультраграф, изображенный на рисунке 2, этим способом будет задан через:
X = {x1, x2, x3, x4, x5}, U = {u1, u2, u3},
Г1X = {Г1xi / i = 1, 5},
где Г1x1 = {u1,u2}, Г1x2 = Г1x3 = Г1x4 = Æ, Г1x5 = {u1, u3},
Г2U = {Г2uj / j = 1, 3},
где Г2u1 = {x2, x3}, Г2u2 = {x4}, Г2u3 = {x5}.
Рассмотренное представление ультраграфа, так же как и матричное, является полным, однако затрудняет выполнение формальных преобразований и просмотр структуры ультраграфа. Например, для того чтобы определить, каким вершинам инцидентно ребро uj Î U, необходимо проверить принадлежность этого ребра всем Г1xi и сформировать подмножество вершин согласно выражению:
Xj– = { xi Î X : uj Î Г1xi }.
Аналогичное замечание справедливо и для определения множества ребер, которым инцидентна вершина xi Î X.
Для задания таких множеств воспользуемся понятием «прообраз множества относительно предиката». По определению прообраз множества – это его образ относительно обратного предиката.
Рассмотрим определение множества ребер, которым инцидентна некоторая вершина xi ультраграфа. Инцидентность ребрам множества U вершин множества X задает предикат-отношение Г2 (U, X), что наглядно иллюстрирует рисунок 3,а. Ребра, которым инцидентны вершины множества X, определяет предикат-отношение Г2-1 (X, U) «вершины множества X инцидентны ребрам множества U». Он является обратным к предикату Г2 (U, X). Элементы предиката Г2-1 (X, U) определяются по правилу:
" uj Î U, "xi Î X (Г2 (uj, xi) = «и» ® Г2-1 (xi, uj) = «и»).
Для ультраграфа, изображенного на рисунке 2, геометрическая интерпретация предиката Г2-1 (X, U) показана на рисунке 3,б, а матрица истинности A2-1 имеет вид
|
|
|
|
u1
|
u2
|
u3
|
|
|
|
x1
|
0
|
0
|
0
|
|
|
|
x2
|
1
|
0
|
0
|
|
A2-1
|
=
|
x3
|
1
|
0
|
0
|
|
|
|
x4
|
0
|
1
|
0
|
|
|
|
x5
|
0
|
0
|
1
|
Зафиксировав в предикате Г2-1 (X, U) вершину xi, получим предикат-свойство Г2-1xi (U) – «вершина xi инцидентна ребрам множества U», характеристическое множество которого является прообразом вершины xi относительно предиката Г2 (X, U), т. е. множеством ребер, которым она инцидентна. Истинность предиката-свойства Г2-1xi (U) задает i-й вектор-строка матрицы предиката Г2-1 (X, U). Из правила определения элементов предиката Г2-1 (X, U) следует, что таблица истинности этого предиката получается транспонированием матрицы инцидентности A2. Отсюда множество ребер Ui–, которым инцидентна вершина xi Î X – ее прообраз относительно предиката Г2 (U, X), – это характеристическое множество i-го вектора-столбца матрицы А2, т. е. предиката-свойства Г2xi (U):
Ui– = Г2xi ={uj Î U : Г2xi (uj) = «и» }, Ui– Í U .
Прообразом множества X относительно предиката Г2 (U, X) будет множество характеристических подмножеств предикатов-свойств Г2xi (U):
Г2X = {Г2xi / xi Î X}.
Аналогично множество вершин, которым инцидентно ребро uj Î U – его прообраз Г1uj относительно предиката Г1 (X, U) – это характеристическое множество Xj– предиката-свойства Г1-1uj (X), соответствующего j-у вектору-строке матрицы истинности А1-1 предиката Г1-1 (U, X), или предиката-свойства Г1uj (X), задаваемого j-м вектором-столбцом матрицы А1:
Xj– = Г1uj = {xi Î X : Г1uj (xi) = «и»}, Xj– Í X.
Прообразом множества U относительно предиката Г1 (X, U) является множество характеристических подмножеств предикатов-свойств Г1uj (X):
Г1U = {Г1uj / uj Î U }.
Для ультраграфа, изображенного на рисунке 2, геометрическая интерпретация предиката Г1-1 (U, X) показана на рисунке 3,б, а матрица истинности A1-1 имеет вид
|
|
|
|
x1
|
x2
|
x3
|
x4
|
x5
|
|
|
|
|
u1
|
1
|
0
|
0
|
0
|
1
|
|
|
A1-1
|
=
|
u2
|
1
|
0
|
0
|
0
|
0
|
.
|
|
|
|
u3
|
0
|
0
|
0
|
0
|
1
|
|
У ультраграфа, показанного на рисунке 2,
Г2X : Г2x1 = Æ, Г2x2 = {u1}, Г2x3 = {u1}, Г2x4 = {u2}, Г2x5 = {u3},
Г1U : Г1u1 = {x1, x5}, Г1u2 = {x1}, Г1u3 = {x5}.
Для данного способа представления ультраграф будем обозначать HU (X, U, Г1X, Г2X, Г2U, Г1U).
Предикаты смежности F1 (X, X) вершин и F2 (U, U) ребер ультраграфа. Установим связь предиката смежности вершин F1 (X, X) с предикатами инцидентности Г1 (X, U) и Г2 (U, X). Рассмотрим для этого пару вершин xi, xt Î X. Для этих вершин связь F1 (X, X) с Г1 (X, U) и Г2 (U, X) определяется выражением
F1(xi, xt) = «и» : $uj Î U (Г1(xi, uj) = «и» & Г2(uj, xt) = «и»). (4)
Здесь xt – вершина, смежная вершине xi, uj – ребро, инцидентное вершине xi, этому ребру инцидентна вершина xt (смотри рисунок 4, а).
Инцидентные вершине xi ребра задает характеристическое множество Ui+ = Г1xi предиката-свойства Г1xi (U). Вершины, инцидентные ребру uj Î Ui+, определяет предикат-свойство Г2uj (X). Таким образом, подставляя в Г2 (U, X) ребра множества Ui+ Í U, получаем множество предикатов-свойств {Г2uj (X)}, uj Î Ui+ = Г1xi, каждый из которых задает вершины, смежные вершине xi по ребру uj.
Поскольку в общем случае |Ui+| >1 и вершина xt Î X будет смежна вершине xi Î X, если xt инцидентна хотя бы одному ребру из Ui+ = Г1xi , вершины, смежные вершине xi в ультраграфе, будут задаваться предикатом – свойством
F1xi (X) = Ú Г2 uj(X). (5)
uj Î Ui+
У ультраграфа, показанного на рисунке 4, а, Ui+ = {uj, uk}. Пусть X = {xi, xt, xr, xp}, т. е. элементы множества X записаны в указанной последовательности. Тогда характеристические вектора предикатов Г2uj (X), Г2uk (X) и F1xi (X) будут:
Г2uj (X) ={0, 1, 1, 0}, Г2uk (X) = {0, 1, 0, 1} и
F1xi (X) = Г2uj (X) Ú Г2uk (X) ={0, 1, 1, 1}.
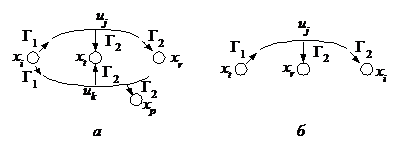
Рисунок 4 – К определению смежности вершин ультраграфа: вершине xi смежны вершины xt, xr, xp (а); вершине xi не смежны вершины xt, xr (б);
Распространяя выкладки для "xi Î X, получим предикат-отношение смежности вершин ультраграфа
F1 (X, X) = { F1xi (X) / xi Î X }. (6)
Матрица истинности этого предиката является матрицей смежности R1 вершин ультраграфа. Элементы этой матрицы по матрицам инцидентности А1 и А2 определяются по правилу:
ì 1 – если $ a1i,j =1 & a2j,t=1,
r1i,t = í
î0 – в противном случае,
где i, t = 1, n; n = | X |, j = 1, m; m = | U |.
Матрица смежности R1 вершин xi Î X ультраграфа, изображенного на рисунке 2, будет:
|
|
|
0
|
1
|
1
|
1
|
0
|
|
|
|
|
0
|
0
|
0
|
0
|
0
|
|
|
R1
|
=
|
0
|
0
|
0
|
0
|
0
|
.
|
|
|
|
0
|
0
|
0
|
0
|
0
|
|
|
|
|
0
|
1
|
1
|
0
|
1
|
|
Наглядно смежность вершин множества X ультраграфа HU (X, U) может быть представлена графом смежности G (X, X). Граф смежности, соответствующий матрице R1, показан на рисунке 5. На этом рисунке вершины ультраграфа изображены кружками, а истинность F1 (xi, xt) – стрелками.
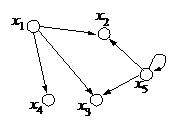
Рисунок 5 – Граф смежности вершин ультраграфа, изображенного на рисунке 2
При выполнении некоторых преобразований ультраграфа и просмотре его структуры бывает необходимо знать, каким вершинам смежна данная. Эта связь задается предикатом F1-1 (X, X) обратным к предикату F1 (X, X). Установим связь предиката F1-1 (X, X) с предикатами инцидентности Г1 (X, U) и Г2 (U, X). Рассмотрим для этого пару вершин xi, xt Î X. Для этих вершин связь F1-1 (X, X) с Г1 (X, U) и Г2 (U, X) определяется выражением
F1-1 (xi, xt) = «и» : $uj Î U (Г2 ( uj, xi) = «и» & Г1 (xt, uj) = «и»). (7)
Здесь xt – вершина, которой смежна вершина xi, uj – ребро, которому инцидентна вершина xi, это ребро инцидентно вершине xt ( смотри рисунок 4, б).
Ребра, которым инцидентна вершина xi, задают характеристическое множество Ui– = Г2xi предиката-свойства Г2xi (U). Вершины, которым инцидентно ребро uj Î Ui+ , определяет предикат-свойство Г1uj (X). Таким образом, подставляя в Г1 (X, U) ребра множества Ui– Í U, получаем множество предикатов-свойств {Г1uj (X)}, uj Î Ui– = Г2xi, каждый из которых определяет вершины, которым смежна вершина xi по ребру uj.
Вершины, которым смежна вершина xi в ультраграфе, будут задаваться предикатом – свойством
F1-1xi (X) = Ú Г1uj (X). (8)
uj Î Ui–
У ультраграфа, показанного на рисунке 4, б, Ui– = {uj}. Пусть X = {xi, xt, xr}, т. е. элементы множества X записаны в указанной последовательности. Тогда характеристические вектора предикатов Г1uj (X) и F1-1xi (X) будут:
Г1uj (X) = {0, 1, 0} и F1-1xi (X) = Г1uj(X) = { 0, 1, 0}.
Распространяя выкладки для "xi Î X, получим обратный предикат-отношение смежности вершин ультраграфа
F1-1 (X, X) = { F1-1xi (X) / xi Î X }. (9)
Матрицу истинности этого предиката обозначим через R1-1. Элемент этой матрицы r1-1i,j = 1 означает, что вершина xi смежна вершине xj (r1i,j = 1 в матрице R1 означает, что вершине xi смежна вершина xj ).
По определению обратного предиката F1‑1(X,X) область его истинности при заданном предикате F1(X, X) задается правилом
"xi , xj Î X (F1 (xi, xj) = «и» ® F1-1(xj, xi) = «и»). (10)
Таким образом, матрица смежности R1-1 ультраграфа (матрица истинности предиката F1-1) получается транспонированием матрицы R1. Матрица R1-1 ультраграфа, показанного на рисунке 2, будет:
|
|
|
0
|
0
|
0
|
0
|
0
|
|
|
|
|
1
|
0
|
0
|
0
|
1
|
|
|
R1-1
|
=
|
1
|
0
|
0
|
0
|
1
|
.
|
|
|
|
1
|
0
|
0
|
0
|
0
|
|
|
|
|
0
|
0
|
0
|
0
|
1
|
|
Предикат смежности F2 (U, U) ребер ультраграфа определяется аналогично предикату смежности вершин F1 (X, X). Формально связь предиката F2 (U, U) с предикатами Г2 (U, X) и Г1 (X, U) устанавливает условие:
F2 (uj, uk) = «и»: $ xi Î X ( Г2(uj, xi) = «и» & Г1(xi, uk) = «и»). (11)
Здесь uk – ребро, смежное ребру uj., а xi – вершина, инцидентная ребру uj, этой вершине инцидентно ребро uk (смотри рисунок 6, а).
Вершины, инцидентные ребру uj Î U, задает характеристическое множество Xj+ = Г2uj предиката-свойства Г2uj (X). Ребра, инцидентные вершине xi Î X, определяет предикат-свойство Г1xi (U). Подставляя в Г1(X,U) вершины множества Xj+ Í X , получаем множество предикатов-свойств {Г1xi (U)}, xi Î Xj+, каждый из которых задает ребра, смежные ребру uj по вершине xi.
Так как в общем случае | Xj+ | > 1 и ребро uk будет смежно ребру uj, если uk инцидентно хотя бы одной вершине из Xj+, то ребра, смежные ребру uj Î U в ультраграфе, будут задаваться предикатом
F2uj(U) = Ú Г1xi (U) . (12)
xi Î Xj+
У ультраграфа, показанного на рисунке 6, а, Xj+ = Г2uj = {xi, xr, xp}.

Рисунок 6 – К определению смежности ребер ультраграфа: ребру uj смежны ребра uk, ud, ut (а); ребро uj смежно ребру uk, ребра uk и ud не смежны (б)
Пусть U = {uj, uk, ud, ut}. Тогда характеристические вектора предикатов-свойств Г1xi (U), Г1xr (U), Г1xp (U) и F2uj (U) будут:
Г1xi (U) = {0, 1, 0, 1},
Г1xr (U) = {0, 0, 0, 1},
Г1xp (U) = {0, 0, 1, 0} и
F2uj (U) = Г1xi (U) Ú Г1xr (U) Ú Г1xp (U) = {0, 1, 1, 1}.
Для " xi Î X получим предикат-отношение смежности ребер ультраграфа
F2 (U, U) = { F2uj (U) / uj Î U } .
Элементы матрицы смежности R2 ребер ультраграфа определяются по правилу:
ì 1 – если $ a2j,i =1 & a1i,k =1,
r2j,k = í
î 0 – в противном случае,
где j, k = 1, m; m = | U |, i = 1, n; n = | X |, a2j,i и a1i,k – элементы матриц инцидентности А2 и А1 соответственно. Матрицы инцидентности А1, А2 и смежности R2 ребер ультраграфа, изображенного на рисунке 7, будут:
|
|
|
1
|
0
|
0
|
|
|
|
0
|
1
|
0
|
1
|
|
|
|
0
|
1
|
0
|
|
|
|
|
0
|
1
|
0
|
|
A2
|
=
|
1
|
0
|
1
|
0
|
|
R2
|
=
|
1
|
0
|
1
|
.
|
|
A1
|
=
|
0
|
0
|
1
|
|
|
|
0
|
0
|
1
|
0
|
|
|
|
0
|
0
|
1
|
|
|
|
|
0
|
0
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Рисунок 7 – К определению матрицы смежности ребер ультраграфа
Граф смежности G (U, U) ребер ультраграфа, соответствующий матрице R2, показан на рисунке 8. Здесь ребра ультраграфа изображены кружками, а истинность F2 (uj, uk) – стрелками.

Рисунок 8 – Граф смежности ребер ультраграфа, показанного на рисунке 7
Для всех uj Î U ребра, которым они смежны, задаются предикатом F2-1 (U, U), обратным предикату F2 (U, U). Значения предиката F2-1 (U, U) по значениям предикатов Г2 (U, X) и Г1 (X, U) определяются по выражению:
F2-1 (uj, uk) = «и»: $ xi Î X ( Г1( xi, uj,) = «и» & Г2( uk , xi) = «и»). (13)
Здесь uk – ребро, которому смежно ребро uj, xi – вершина, которой инцидентно ребро uj, эта вершина инцидентна ребру uk (смотри рисунок 6,б).
Вершины, которым инцидентно ребро ujÎU, задает характеристическое множество Xj– = Г1uj предиката-свойства Г1uj (X). Ребра, которым инцидентна вершина xi Î X, определяет предикат-свойство Г2xi (U). Подставляя в Г2 (X, U) вершины множества Xj– Í X , получаем множество предикатов-свойств {Г2xi (U)}, xi Î Xj– , каждый из которых задает ребра, которым смежно ребро uj по вершине xi.
Ребра, которым смежно ребро uj Î U в ультраграфе, будут задаваться предикатом
F2-1uj (U) = Ú Г2xi (U) . (14)
xi Î Xj–
У ультраграфа, показанного на рисунке 6, б, Xj– = Г1uj = {xi}. Пусть U = {uk, uj}. тогда характеристические вектора предикатов-свойств Г2xi (U) и F2-1uj (U) будут:
Г2xi (U) = {1, 0} и F2-1uj (U) = {1, 0}.
Для "xiÎX получим обратный предикат-отношение смежности ребер ультраграфа
F2-1 (U, U) = { F2-1uj (U) / uj Î U} .
Матрицу истинности этого предиката обозначим как R2-1. Элемент этой матрицы r2-1i,j =1 означает, что ребро ui смежно ребру uj ультраграфа.
Предикат F2-1 (U, U), как обратный предикату F2 (U, U), получается по правилу:
" uj, uk Î U (F2 (uj, uk) = «и» ® F2-1 (uk, uj) = «и»). (15)
Отсюда матрица истинности R2-1 предиката F2-1 (U, U) является транспонированной матрицей R2. Для ультраграфа, показанного на рисунке 7, эта матрица будет:
|
|
|
0
|
1
|
0
|
|
|
R2-1
|
=
|
1
|
0
|
0
|
.
|
|
|
|
0
|
1
|
1
|
|
Образы и прообразы множеств X и U относительно предикатов смежности вершин F1 (X, X) и ребер F2 (U, U) соответственно. Для каждой вершины xi Î X ультраграфа HU (X, U) ее образ F1xi относительно предиката смежности F1 (X, X) – множество смежных ей вершин Xi+, определяется характеристическим множеством предиката-свойства F1xi (X)
Xi+ = F1xi = {xk Î X: F1xi (xk) = «и»}.
Истинность предиката-свойства F1xi (X) задается i-м вектором-строкой матрицы R1.
Множество вершин Xi–, которым смежна вершина xi , т. е. ее прообраз F1-1xi относительно предиката F1 (X, X), является характеристическим множеством предиката-свойства F1-1xi ( X) :
Xi– = F1-1xi = { xk Î X: F1-1xi (xk) = «и» }.
Истинность предиката-свойства F1-1xi (X) задается i-м вектором-строкой матрицы R1-1 или соответствующим вектором-столбцом матрицы R1.
По аналитическому представлению ультраграфа в виде HU (X, U, Г1X, Г2X, Г1U, Г2U) для каждой вершины xiÎX ее образ F1xi определяется на основании (5) по правилу
F1xi = È Г2uj , (16)
ujÎГ1xi
а прообраз F1-1xi в соответствии с (8) по выражению
F1-1xi = È Г1uj . (17)
ujÎГ2xi
Образ и прообраз множества вершин X относительно предиката смежности F1 (X, X) будут:
F1X = {F1xi / xi Î X}
и F1-1X = {F1-1xi / xi Î X}.
Для ультраграфа, изображенного на рисунке 2, множества образов F1X и прообразов F1-1X его вершин относительно предиката смежности F1 будут:
F1X = {F1xi / i = 1,5}: F1-1X = {F1-1xi / i = 1,5}:
F1x1 = {x2, x3, x4}, F1-1x1 = Æ, F1-1x4 = {x1},
F1x2 = F1x3 = F1x4 = Æ, F1-1x2 = {x1, x5}, F1-1x5 = {x5}.
F1x5 = {x2, x3, x5}, F1-1x3 = {x1, x5},
Образ F2uj ребра uj Î U ультраграфа HU (X, U) относительно предиката F2 (U, U), т. е. множество Uj+ смежных ему ребер, определяется характеристическим множеством предиката-свойства F2uj (U):
Uj+ = F2uj = {ukÎU: F2uj (uk) = «и»}.
Истинность предиката F2uj (U) задается j-м вектором-строкой матрицы R2.
Прообраз F2-1uj ребра ujÎU относительно предиката F2 (U, U), т. е. множество ребер Uj–, которому это ребро смежно, является характеристическим множеством предиката-свойства F2-1uj (U):
Uj– = F2-1uj = {ukÎU: F2-1uj (uk) = «и»}.
Истинность предиката F2-1uj (U) задается j-м вектором-строкой матрицы R2‑1 или соответствующим вектором-столбцом матрицы R2.
По аналитическому представлению ультраграфа для каждого ребра ujÎU его образ F2uj определяется на основании (12) по правилу
F2uj = È Г1xi , (18)
xi Î Г2uj
а прообраз F2-1uj в соответствии с (14) по выражению
F2-1uj = È Г2xi . (19)
xi Î Г1uj
Образ и прообраз множества ребер U относительно предиката смежности F2 (U, U) будут:
F2U = {F2uj / uj Î U}
и F2-1U = {F2-1uj / uj Î U}.
Для ультраграфа, изображенного на рисунке 7, множества образов F2U и прообразов F2-1U его ребер относительно предиката смежности F2 будет:
F2U = {F2uj / j = 1,3}: F2-1U = {F2-1uj / j = 1,3}:
F2u1 = {u2}, F2-1u1 = {u2},
F2u2 = { u1, u3}, F2-1u2 = {u1},
F2u3 = {u3}, F2-1u3 = {u2, u3}.
Отметим в заключение, что совокупность матриц смежности, а также образов и прообразов множеств вершин X и ребер U ультраграфа HU (X, U) относительно предикатов смежности вершин F1 (X, X) и ребер F2 (U, U) задает ультраграф не полностью.
Если в ходе анализа и преобразования ультраграфа необходимо знать связи вершин и ребер, определяемые как предикатами инцидентности, так и предикатами смежности, ультраграф может быть задан в форме HU (X, U, Г1X, Г2X, Г2U, Г1U, F1X, F1-1X, F2U, F2-1U) либо необходимым подмножеством образов и прообразов вершин и ребер относительно предикатов инцидентности и смежности с указанием в скобках используемого набора образов и/или прообразов. Аналогично будем поступать и в отношении гиперграфа, обыкновенного ориентированного и неориентированного графов, которые будут рассмотрены ниже.
Характеристики вершин и ребер ультраграфа. К характеристикам вершин ультраграфа относятся:
· r+(xi) – полустепень исхода, т. е. количество ребер, инцидентных вершине xi Î X. По матрице инцидентности A1 показатель рассчитывается по формуле:
m
r+(xi) = S a1i,j.
j=1
Для ультраграфа, изображенного на рисунке 2, r+(x1) =2.
При аналитическом представлении ультраграфа этот показатель определяется по выражению:
r+(xi) = | Г1xi |.
Для ультраграфа, показанного на рисунке 9, Ui+ = Г1xi = {u1} и r+(xi) = 1;
· r- (xi) – полустепень захода, т. е. количество ребер, которым инцидентна вершина xi Î X. По матрице инцидентности A2 показатель рассчитывается по формуле:
m
r- (xi) = S a2j,i.
j=1
Для ультраграфа, изображенного на рисунке 2, r-(x1) = 0.
При аналитическом представлении ультраграфа этот показатель определяется по выражению:
r- (xi) = | Г2xi |.
Для ультраграфа (смотри рисунок 9) Ui– = Г2xi = {u2, u3} и r-(xi) = 2;
· A(xi) ={ak (xi) / k = 1, |Ui+ |} – вектор, элемент которого ak (xi) равен количеству вершин, инцидентных ребру uj Î Ui+ = Г1xi:
ak (xi) = | Г2uj |.

Рисунок 9 – К определению характеристик вершин ультраграфа
Для ультраграфа, показанного на рисунке 9, образ вершины xi будет
Г1xi = {u1}, а прообраз ребра u1 – Г2u1 = { xk, xr }. Отсюда A(xi) ={2};
· B(xi) = {bk (xi) / k=1, |Ui+|} – вектор, каждый его элемент bk (xi) равен количеству вершин, которым инцидентно ребро uj Î Ui+ = Г1xi:
bk (xi) = | Г1uj | -1.
Для ребра u1Î Г1xi (смотри рисунок 9) его прообраз Г1u1 = {xi, xt} тогда B(xi) = {1};
· C(xi) ={ck (xi) / k = 1, |Ui–|} – вектор, элемент которого ck (xi) равен количеству вершин, инцидентных ребру uf Î Ui– = Г2xi:
ck (xi) = | Г2uf | -1.
Для вершины xi (смотри рисунок 9) Г2xi = {u2, u3}. Для этих ребер их образы Г2u2 = {xi, xq}, Г2u3 = {xi, xс}. Отсюда C(xi) = {1, 1};
· D(xi) = {dk (xi) / k = 1, |Ui–|} – вектор, каждый его элемент dk (xi) равен количеству вершин, инцидентных ребру uf Î Ui–= Г2xi:
dk (xi) = | Г1uf | .
Для ребер u2, u3 Î Г2xi того же ультраграфа их прообразы Г1u2 = {xl} и Г1u3 = {xp}. Тогда D(xi) = {1, 1};
· s+(xi) – количество вершин, смежных вершине xi Î X. По матрице смежности R1 этот показатель рассчитывается по формуле:
m
s+(xi) = S r1i,j.
j=1
Для вершины x1 ультраграфа, показанного на рисунке 2, s+( x1) = 3.
При известных образах вершин относительно предиката смежности F1(X, X)
s+(xi) = | F1xi |.
Для вершины xi ультраграфа, изображенного на рисунке 9, Г1xi = {u1}, F1xi = Г2u1 = { xk, xr }, s+(xi) = 2;
· s-(xi)– количество вершин, которым смежна вершина xi Î X. При матричном представлении ультраграфа показатель рассчитывается как
m m
s-(xi) = S r1-1i,j или s-(xi) = S r1j,i
j=1 j=1
по матрицам смежности R1-1 и R1 соответственно. Для вершины x2 ультраграфа, изображенного на рисунке 2, s- (x2) = 2.
По прообразу вершины относительно предиката смежности F1 (X, X) показатель определяется по выражению
s- (xi) = | F1-1xi | .
Для вершины xi ультраграфа, изображенного на рисунке 9, Г2xi = {u2, u3}, Г1u2 È Г1u3 = F1-1xi = {xl, xp }, s-(xi) = 2;
· e(xi) = |{uj Î U : Г1uj = Г2uj = xi}| – количество петель вершины xi.
Характеристики ребер ультраграфа:
· r+(uj)– количество вершин множества Xj+ = Г2uj, инцидентных ребру uj. По матрице инцидентности А2 этот показатель рассчитывается по формуле:
n
r+(uj) = S a2j,i .
i=1
Для ультраграфа, изображенного на рисунке 2, r+(u1) = 2.
При аналитическом представлении ультраграфа этот показатель определяется по выражению:
r+(uj) = | Г2 uj |.
Для ребра u1 ультраграфа (смотри рисунок 10) Г2u1={xi, xk, xr} и r+(u1) = 3;
· r-(uj) = | Г1uj | – количество вершин множества Xj– = Г1uj, которым инцидентно ребро uj. По матрице инцидентности A1 показатель рассчитывается по формуле:
n
r-(uj) = S a1i,j.
i=1
Для ультраграфа, изображенного на рисунке 2, r-(u1) = 2.
При аналитическом представлении ультраграфа этот показатель определяется по выражению:
r-(uj) = | Г1uj |.
Для ребра u1 ультраграфа, показанного на рисунке 10, Г1u1 = {xt}, r- (u1) = 1;
· A(uj) = {ak (uj) / k = 1, | Xj+ |} – вектор, элемент которого ak(uj) равен количеству ребер, инцидентных вершине xi Î Xj+ = Г2uj :
ak (uj) = | Г1xi |.

Рисунок 10 – К определению характеристик ребер ультраграфа
Для ребра u1 ультраграфа, показанного на рисунке 10, Г2u1 ={ xi, xk, xr }, и для вершин xi, xk, xr их образы равны Г1xi ={u2, u3}, Г1xk = Æ, Г1xr = Æ. Тогда A(u1) = {2, 0, 0};
· B(uj) = {bk (uj) / k =1, | Xj+ |} – вектор, каждый его элемент bk (uj) равен количеству ребер, которым инцидентна вершина xi Î Xj+ = Г2uj:
bk (uj) = | Г2xi | -1.
Для всех вершин xi, xk, xr Î Г2u1 (смотри рисунок 10) прообразы Г2xi = Г2xk = Г2xr = {u1} и B(u1) = {0, 0, 0};
· C(uj ) ={ck (uj) / k = 1, | Xj– |} – вектор, элемент которого ck (uj) равен количеству ребер, инцидентных вершине xiÎ Xj– = Г1uj:
ck (uj) = | Г1xi | -1.
Для ребра u1 (смотри рисунок 10) Г1u1 ={xt} и для вершины xt ее образ Г1xt = {u1, u4 } и C(u1) ={1};
· D(uj) = { dk(uj) / k =1, | Xj– |} – вектор, каждый его элемент dk(uj) равен количеству ребер, которым инцидентна вершина xi Î Xj– = Г1uj :
dk (uj) = | Г2xi | .
Для вершины xt Î Г1u1 ее прообраз Г2 xt = Æ и D(uj) = {0};
· s+(uj) – количество ребер, смежных ребру uj Î U. По матрице смежности R2 этот показатель рассчитывается по формуле:
m
s+(uj) = S r2j,i.
i=1
Для ребра u2 ультраграфа, показанного на рисунке 7, s+(u2) = 2.
При известных образах ребер относительно предиката смежности F2 (U, U):
s+(uj) = | F2uj |.
Для ребра u1 ультраграфа, изображенного на рисунке 10, его образ Г2u1={xi, xk, xr }, образы этих вершин Г1xi = {u2, u3}, Г1xk = Г1xr = Æ. Множество ребер, смежных ребру u1, F2u1 = Г1xi Ú Г1xk Ú Г1xr и F2 u1={u2,u3}. Тогда r+(u1) = 2;
· s-(uj) – количество ребер, которым смежно ребро ujÎU. При известных матрицах смежности R2 или R2-1 этот показатель рассчитывается по формуле:
m m
s-(uj) = S r2i,j или s-(uj) = S r2-1j,i .
i=1 i=1
Для ребра u3 ультраграфа, показанного на рисунке 7, s-( u3) = 2.
При известных прообразах ребер, т. е. их образах относительно предиката смежности F2-1 (U, U), показатель определяется по выражению:
s-(uj) = | F2-1uj |.
Для ребра u1 (смотри рисунок 10) его прообраз Г1u1 = {xt}. Прообраз этой вершины Г2xt = Æ, отсюда F2-1u1 = Æ и s-(u1) = 0.
Гиперграфы. Данный вид графа получим в соответствии со сформулированным выше определением при выполнении условия (1) в том случае, когда
"xi, xk Î X, uj Î U (Г1(xi,uj) = «и»®Г2(uj,xi) = «и» &
Г2 (uj,xk) = «и» ® Г1(xk,uj) = «и») (20)
и $ uj Î U |Г2uj | > 2 (21)
или $ uj Î U |Г2uj | = 1. (22)
Условие (20) означает, что предикат-отношение Г2 (U, X) является обратным к предикату-отношению Г1 (X, U). Тогда гиперграф можно определить как два непересекающихся множества вершин X и ребер U, на элементах которых задана пара двуместных предикатов-отношений инцидентности Г1 (X, U) и Г2 (U, X) таких, что Г2 (U, X) = Г1-1 (X, U).
Вектор-строка таблицы истинности двуместного предиката-отношения Г1 (X, U) – матрицы инцидентности вершины-ребра A1 совпадает с вектором-столбцом таблицы истинности предиката Г2 (U, X) – матрицы инцидентности ребра-вершины A2. По определению предикаты эквивалентны, если их таблицы истинности совпадают. Отсюда следует, что:
· предикат-свойство Г1xi (U) – «вершине xi инцидентны ребра множества U» эквивалентен предикату-свойству Г2xi (U) –«вершина xi инцидентна ребрам множества U»,
· предикат-свойство Г2uj (X) – «ребру uj инцидентны вершины множества X» эквивалентен предикату-свойству Г1uj (X) – «ребро uj инцидентно вершинам множества X».
Таким образом не существует отличия в связях между вершинами множества X и ребрами множества U, задаваемых предикатами-инциденторами Г1 и Г2. Следовательно, содержательно эти предикаты можно трактовать как «вершины множества X и ребра множества U инцидентны» – предикат Г1 (X, U) и «ребра множества U и вершины множества X инцидентны» – предикат Г2 (U, X). Отсюда, гиперграф будет полностью задан, если заданы множество вершин X, ребер U и один из предикатов Г1 (X, U) или Г2 (U, X).
С учетом сказанного в гиперграфе:
– вершины xi и xk смежны, если существует ребро uj, такое, что вершина xi и ребро uj, ребро uj и вершина xk инцидентны;
– ребра uj и uk смежны, если существует вершина xi, такая, что ребро uj и вершина xi, вершина xi и ребро uk инцидентны.
В дальнейшем, рассматривая связь некоторой вершины с ребром, будем говорить «ребро, инцидентное вершине», имея в виду, что для них справедливо «вершина и ребро инцидентны». Аналогично «вершина, инцидентная ребру» соответствует высказыванию «ребро и вершина инцидентны».
При геометрическом представлении гиперграфа вершины изображаются кружками, ребра – в виде контуров, а расположение вершины xi внутри ребра uj означает истинность Г1 (xi,uj), следовательно и Г2 (uj,xi). На рисунке 11,а приведено такое изображение гиперграфа, а на рисунке 11,б – его представление в виде двудольного графа (сравните с рисунками 2 и 3 соответственно).

Рисунок 11 – Гиперграф (а) и его представление в виде двудольного графа (б)
Представление гиперграфа матрицами инцидентности. Поскольку матрица истинности предиката Г2 (U, X) является транспонированной матрицей предиката Г1 (X, U), гиперграф при матричном представлении будет полностью задан, если определены элементы одной из них. В качестве матрицы инцидентности AH гиперграфа будем использовать матрицу истинности предиката Г1 (X, U), размером n´m, где n = |X|, а m = |U|. Элементы этой матрицы задают связь между вершинами и ребрами гиперграфа и определяются по правилу
ì 1 – если Г1 (xi,uj) = «и»
a i,j = í ,
î 0 – если Г1(xi,uj) = «л»,
где i = 1, n, j = 1, m .
Матрица инцидентности гиперграфа, изображенного на рисунке 11, имеет вид
|
|
|
|
u1
|
u2
|
u3
|
|
|
|
|
x1
|
1
|
1
|
0
|
|
|
|
|
x2
|
1
|
0
|
0
|
|
|
AH
|
=
|
x3
|
1
|
0
|
0
|
.
|
|
|
|
x4
|
0
|
1
|
0
|
|
|
|
|
x5
|
1
|
0
|
1
|
|
Представление гиперграфа образами вершин и ребер относительно предикатов Г1 (X, U) и Г2 (U, X). В гиперграфе образ Г1xi вершины xi Î X относительно предиката Г1 (X, U) – это подмножество Ui ÍU инцидентных ей ребер. Он является характеристическим множеством предиката-свойства Г1xi (U), т. е. вектора-строки матрицы АH. Множество подмножеств ребер, инцидентных вершинам xiÎX, т. е. образ множества X относительно предиката Г1(X,U), будет
Г1X = {Г1xi /xi Î X}, где Г1xi = Ui Í U, Г1xi = {uj Î: Г1xi(uj) = «и»}. (23)
Образом Г2uj ребра uj Î U относительно предиката Г2 (U, X) является подмножество Xj Í X вершин, инцидентных этому ребру. Образ множества ребер U относительно того же предиката будет задаваться множеством характеристических подмножеств предикатов-свойств Г2uj (X), т. е. столбцов матрицы АH :
Г2U = {Г2uj /ujÎU}, где Г2uj = Xj Í X, Г2uj ={ xi ÎX: Г2uj(xi) = «и»}. (24)
Гиперграф данным способом будет задан, если заданы множества вершин X, ребер U и их образы, т. е. множества подмножеств Г1X и Г2U. При таком представлении будем обозначать его как H(X,U,Г1X,Г2U). Гиперграф, изображенный на рисунке 11, этим способом будет задан через:
X={x1, x2, x3, x4, x5}, U={u1, u2, u3},
Г1X ={Г1xi /i=1,5},
где Г1x1 = {u1, u2}, Г1x2 ={u1}, Г1x3 = {u1}, Г1x4 ={ u2}, Г1x5 ={ u1,u3},
Г2U={ Г2uj / j=1,3},
где Г2u1 = { x1, x2, x3, x5}, Г2u2 = { x1, x4}, Г2u3 = {x5}.
Рассмотренное представление гиперграфа, так же как и матричное, является полным.
Предикаты смежности F1 (X, X) вершин и F2 (U, U) ребер гиперграфа. Установим связь предиката смежности вершин F1 (X, X) с предикатами инцидентности Г1 (X, U) и Г2 (U, X). Рассмотрим для этого пару вершин xi, xk Î X. Для этих вершин связь F1 (X, X) с Г1 (X, U) и Г2 (U, X) определяется выражением
F1(xi, xk) = «и» : $uj Î U (Г1(xi, uj) = «и» & Г2(uj, xk) = «и»). (25)
Инцидентные вершине xi ребра задает характеристическое множество Ui =Г1xi предиката-свойства Г1xi (U). Вершины, инцидентные ребру ujÎUi , определяет предикат-свойство Г2uj (X). Таким образом, подставляя в Г2 (U, X) ребра множества Ui Í U, получаем множество предикатов-свойств {Г2uj (X)}, uj Î Ui = Г1xi, каждый из которых задает вершины, смежные вершине xi по ребру uj.
Поскольку вершина xk Î X будет смежна вершине xi Î X, если она инцидентна хотя бы одному ребру из Ui = Г1xi , вершины, смежные вершине xi, будут задаваться предикатом – свойством
F1xi (X) = Ú Г2uj (X), (26)
ujÎUi
где Г2uj (xi) = «л», если |Г2uj| > 1.
Это вытекает из того, что в гиперграфе Г1(xi, uj) = «и» ®Г2(uj, xi) = «и», поэтому при определении предиката смежности F1xi (X) по этой формуле без учета условия |Г2uj| > 1 каждая вершина будет смежна самой себе, даже если у нее нет петли (смотри рисунок 11 и матрицу AH). Следовательно, в формуле (24) значение одноместного предиката-свойства Г2uj (X) при x = xi , т. е. Г2uj (xi), должно принимать значение «ложь», если |Г2uj| > 1 (uj не является петлей).
У гиперграфа, показанного на рисунке 11, U1 = Г1x1 = {u1, u2} и характеристические вектора предикатов Г2u1 (X), Г2u2 (X) равны:
Г2u1 (X) ={1, 1, 1, 0, 1}, Г2u2 (X) = {1, 0, 0, 1, 0}. После присваивания Г2u1(x1) и Г2u2(x1) значения «0» получаем
F1x1 (X) = Г2u1(X) Ú Г2u2(X) ={0, 1, 1, 1, 1},т. е. вершина x1 смежна вершинам x2, x3, x4, x5.
Распространяя выкладки для "xi Î X, получим предикат-отношение смежности вершин гиперграфа
F1 (X, X) = {F1xi (X) / xi Î X }. (27)
Матрица истинности этого предиката является матрицей смежности R1 вершин гиперграфа. Элементы этой матрицы по матрице инцидентности АH определяются по правилу:
ì 1 – если i ¹ k & $ ai, j = 1 & ak, j = 1,
r1i,k = í 1 – если i = k & $ ai, j = 1 & f = 1,
î 0 – в противном случае,
где i, k =1, n; n = | X |, j =1, m; m = | U |, ai, j , ak, j и at, j – элементы матрицы инцидентности АH гиперграфа, а
n
f = S at,j.
t=1
Матрица смежности R1 вершин xi Î X гиперграфа, изображенного на рисунке 11, будет:
|
|
|
0
|
1
|
1
|
1
|
1
|
|
|
|
|
1
|
0
|
1
|
0
|
1
|
.
|
|
R1
|
=
|
1
|
1
|
0
|
0
|
1
|
|
|
|
|
1
|
0
|
0
|
0
|
0
|
|
|
|
|
1
|
1
|
1
|
0
|
1
|
|
В соответствии со свойством (20) матрица R1 симметрична относительно главной диагонали. Граф смежности вершин гиперграфа, изображенного на рисунке 11, показан на рисунке 12.

Рисунок 12 – Граф смежности вершин гиперграфа, изображенного на рисунке 11
Определим предикат смежности F2 (U, U) ребер гиперграфа. Формально связь предиката F2 (U, U) с предикатами Г2 (U, X) и Г1 (X, U) устанавливает условие:
F2(uj, uk) = «и»: $xiÎX ( Г2(uj, xi)= «и» & Г1(xi, uk)= «и»). (28)
Вершины, инцидентные ребру ujÎU, задает характеристическое множество Xj = Г2uj предиката-свойства Г2uj (X). Ребра, инцидентные вершине xiÎX, определяет предикат-свойство Г1xi (U). Подставляя в Г1 (X, U) вершины множества Xj Í X , получаем множество предикатов-свойств {Г1xi (U)}, xiÎXj , каждый из которых задает ребра, смежные ребру uj по вершине xi.
Ребра, смежные ребру uj Î U в гиперграфе, будут задаваться предикатом
F2uj(U) = Ú Г1xi (U) , (29)
xiÎXj
где Г1xi (uj) = «л», если |Г2uj| >1, так как в гиперграфе на основании (20) Г2 (uj, xi) = «и»® Г1 (xi, uj) = «и», поэтому, не присваивая Г1xi (U) значения «ложно» при u = uj и выполнении указанного условия, получили бы, что каждое ребро, если оно и не является петлей, смежно самому себе.
У гиперграфа, показанного на рисунке 11, Г2u1 = {x1, x2, x3, x5} и характеристические вектора предикатов Г1x1 (U), Г1x2 (U), Г1x3 (U), Г1x5 (U) имеют значения:
Г1x1 (U) = {1, 1, 0}, Г1x2 (U) = {1, 0, 0},
Г1x3 (U) = {1, 0, 0}, Г1x5 (U) = {0, 0, 1}.
После присваивания Г1x1 ( u1), Г1x2 ( u1), Г1x3 ( u1) и Г1x5 ( u1) значения «0» получаем
F2u1 (U) = {0, 1, 0} Ú {0, 0, 0} Ú {0, 0, 0} Ú {0, 0, 1} = {0, 1, 1}, т. е. ребро u1 смежно ребрам u2 и u3.
Для " uj Î U получим предикат-отношение смежности ребер гиперграфа
F2 (U, U) = {F2uj (U) / ujÎU} . (30)
Элементы матрицы смежности R2 ребер гиперграфа определяются по правилу:
ì 1 – если j ¹ k & $ ai,j = 1 & ai,k = 1,
r2j,k = í 1– если j = k & $ ai,j = 1 & f = 1,
î 0 – в противном случае,
где j,k = 1, m; m = | U |, i = 1, n; n = | X |, ai,j, ai,k и at,j – элементы матри-
n
цы инцидентности АH гиперграфа, а f = S at, j.
t =1
Матрица смежности R2 ребер uj Î U гиперграфа, изображенного на рисунке 11, будет:
|
|
|
0
|
1
|
1
|
|
|
R2
|
=
|
1
|
0
|
0
|
.
|
|
|
|
1
|
0
|
1
|
|
Матрица R2, так же как и R1, симметрична относительно главной диагонали. Граф смежности ребер этого же гиперграфа представлен на рисунке 13.

Рисунок 13 – Граф смежности ребер гиперграфа, изображенного на рисунке 11
Здесь ребра гиперграфа изображены кружками, а истинность F2(uj, ur) – линиями, их соединяющими.
Образы множеств X и U относительно предикатов смежности вершин F1 (X, X) и ребер F2 (U, U) соответственно. Для каждой вершины xiÎX гиперграфа H (X, U) ее образ F1xi относительно предиката смежности F1 (X, X) (множество смежных ей вершин Xi) определяется характеристическим множеством предиката-свойства F1xi ( X)
Xi = F1xi = {xk Î X : F1xi (xk) = «и»}.
Истинность предиката-свойства F1xi (X) задается i-м вектором-строкой матрицы R1.
По аналитическому представлению гиперграфа в форме H (X, U, Г1X, Г2U) для каждой вершины xi Î X ее образ F1xi на основании (26) определяется по правилу
F1xi = È{ Г2uj \ xi : | Г2uj | > 1 Ú Г2uj : | Г2uj | = 1}. (31)
uj Î Г1xi
Для гиперграфа, изображенного на рисунке 11, множество образов F1X = { F1xi / xi Î X } его вершин относительно предиката смежности F1 (X, X) будет:
F1X = {F1xi / i =1,5}: F1x1 = {x2, x3, x4, x5}, F1x2 = {x1, x3, x5}, F1x3 = {x1, x2, x5}, F1x4 = { x1}, F1x5 = {x1, x2, x3, x5}.
Образ F2uj ребра ujÎU гиперграфа H (X, U) относительно предиката F2 (U, U), т. е. множество Uj смежных ему ребер, определяется характеристическим множеством предиката-свойства F2uj (U):
Uj = F2uj = { uk Î U: F2uj (uk) = «и» }.
Истинность предиката F2uj (U) задается j-м вектором-строкой матрицы R2.
По аналитическому представлению гиперграфа образ каждого ребра F2uj определяется на основании (29) по выражению
F2uj = È{Г1xi \ uj : | Г2uj | >1 Ú Г1xi:| Г2uj | =1}. (32)
xi Î Г2uj
Для гиперграфа, изображенного на рисунке 11, множество образов F2U = {F2uj / uj Î U} его ребер относительно предиката смежности F2 (U, U) будет:
F2U = {F2uj / j = 1, 3}: F2u1 = {u2, u3}, F2u2 = {u1}, F2u3 = {u1, u3}.
Так же как для ультраграфа, совокупность матриц смежности, а также образов множеств вершин X и ребер U гиперграфа H (X, U) относительно предикатов смежности вершин F1 (X, X) и ребер F2 (U, U) задает гиперграф не полностью.
Если в ходе анализа и преобразования гиперграфа необходимо знать связи вершин и ребер, определяемые как предикатами инцидентности, так и предикатами смежности, гиперграф может быть задан в форме H (X, U, Г1X, Г1U, F1X, F2U) либо необходимым сочетанием образов вершин и ребер относительно предикатов инцидентности и смежности.
Характеристики вершин и ребер гиперграфа. К характеристикам вершин гиперграфа относятся:
· r(xi) – локальная степень вершины (количество ребер множества Ui = Г1xi, инцидентных вершине xi Î X). По матрице инцидентности AH этот показатель рассчитывается как:
m
r(xi) = S ai,j.
j=1
При аналитическом представлении гиперграфа характеристика определяется по формуле :
r(xi) = | Г1xi |.
Для гиперграфа, изображенного на рисунке 11, r(x1) = 2 ( Г1x1 ={u1, u2});
· s(xi) – количество вершин, смежных вершине xi Î X. По матрице смежности R1 характеристика рассчитывается по выражению:
m
s(xi) = S r1i,j.
j=1
При аналитическом представлении гиперграфа показатель определяется по формуле:
s(xi) = | F1xi |.
Для гиперграфа, изображенного на рисунке 11, s(x2) = 3 (F1x2 ={x1, x3, x5});
· e(xi) – количество петель при вершине гиперграфа. По матрице инцидентности AH характеристика определяется как количество столбцов, для которых
n
S ai,j = 1.
i=1
При аналитическом представлении гиперграфа показатель равен:
e(xi) = |{uj Î Г2xi : | Г2uj | = 1}|.
Характеристики ребер гиперграфа:
· r(uj) – количество вершин множества X, инцидентных ребру uj. По матрице инцидентности АH этот показатель рассчитывается по формуле:
n
r(uj) = S ai,j .
i=1
Для гиперграфа, изображенного на рисунке 11, s(u1) = 4.
При аналитическом представлении гиперграфа этот показатель определяется по выражению:
r(uj) = | Г2 uj |.
Для ребра u2 того же гиперграфа Г2u2 = {x1,x5} и r(u2) = 2;
· s(uj)– количество ребер, смежных ребру ujÎU. По матрице смежности R2 этот показатель рассчитывается по формуле:
m
s(uj) = S r2j,k.
k=1
Для ребра u1 гиперграфа, показанного на рисунке 11, s(u1) = 2.
При известных образах ребер относительно предиката смежности F2 (U, U):
s(uj) = | F2uj |.
Для ребра u2 гиперграфа, изображенного на рисунке 11, F2u2 = {u1}, тогда s(u1) = 1;
· Q(uj) = {qk(uj) / k = 1, | Uj|}– вектор, каждый элемент которого qk(uj) равен количеству вершин множества Xj = Г2uj, инцидентных ребру ui Î Uj = F2uj:
qk(uj) = | Г2uj Ç Г2ui |.
Для ребра u1 гиперграфа, показанного на рисунке 14,a, X1 = Г2u1 = {x1, x2, x3, x4}, U1 = F2u1 = {u2, u3}, Г2u2 = {x1, x2, x5}, Г2u3 = {x3, x6}, q1(u1) = | Г2u1 Ç Г2u2 | = 2, q2(u1) = | Г2u1 Ç Г2u3 | = 1 (сравните с гиперграфом на рисунке 14,б).

Рисунок 14 – К определению характеристики Q(uj) ребер гиперграфа
Обыкновенные ориентированные графы. Этот вид графа получим в том случае, если предикаты Г1 (X, U) и Г2 (U, X) таковы, что
" uj Î U (|Г1uj| = |Г2uj| = 1) , (33)
т. е. в графе нет ребер, суммарное количество вершин, которым оно инцидентно и которые инцидентны ему, больше двух. Данное условие допускает возможность существования в ориентированном графе петель. Из анализа (2) и (33) видно, что обыкновенный ориентированный граф является частным случаем ультраграфа.
Ребра ориентированного графа G (X, U) обычно в литературе называют дугами и изображают стрелками, соединяющими соответствующие пары вершин. С учетом (1) примем такое же изображение, имея в виду, что дуга uj идет из вершины xi в вершину xk, если Г1 (xi,uj) = «и» & Г2 (uj,xk) = «и», и соединяет вершину xk с вершиной xi, если Г1 (xk,uj) = «и» & Г2 (uj,xi) = «и». Такое изображение ориентированного графа показано на рисунке 15,а, а в виде двудольного графа – на рисунке 15,б.

Рисунок 15 – Ориентированный граф (а) и его представление в виде двудольного (б)
Представление ориентированного графа матрицами инцидентности. Как и для ультраграфа полным способом формального задания ориентированного графа является его представление через две матрицы инцидентности А1 и A2, где А1– матрица истинности предиката Г1 (X, U) и А2 – матрица истинности предиката Г2 (U, X).
Элементы этих матриц определяются по тем же правилам, что и для ультраграфа. Напомним, что матрица А1 задает инцидентность между вершинами и ребрами, а матрица А2 –между ребрами и вершинами.
Матрицы А1 и А2 ориентированного графа, показанного на рисунке 15, имеют вид:
|
|
|
|
u1
|
u2
|
u3
|
u4
|
u 5
|
|
|
|
|
x1
|
x2
|
x3
|
x4
|
|
|
|
|
x1
|
1
|
1
|
0
|
0
|
0
|
|
|
|
u1
|
0
|
1
|
0
|
0
|
|
|
|
|
x2
|
0
|
0
|
1
|
0
|
0
|
|
|
|
u2
|
0
|
0
|
0
|
1
|
|
|
A1
|
=
|
x3
|
0
|
0
|
0
|
1
|
0
|
,
|
A2
|
=
|
u3
|
0
|
0
|
0
|
1
|
.
|
|
|
|
x4
|
0
|
0
|
0
|
0
|
1
|
|
|
|
u4
|
0
|
1
|
0
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u 5
|
0
|
0
|
0
|
1
|
|
В ряде работ вместо двух матриц инцидентности А1 и А2 предлагается использовать одну, обозначим ее как А. Элементы этой матрицы определяются по правилу:
ì 1 – если вершина xi является началом дуги uj,
ai ,j = í -1– если вершина xi является концом дуги uj,
î 0 – в противном случае,
где i = 1, n; n = | X |, j =1, m; m = | U |.
Нетрудно убедиться, что матрица А является матрицей истинности предиката T(X,U) = Г1(X,U) Ú Г2-1(X,U), в котором истинность значения Г1(xi,uj) обозначена как «1», а значения Г2-1(xi,uj) как «-1»:
ai,j = 1 – если вершина xi является началом дуги uj, и Г1(xi,uj) = «и»,если ребро uj инцидентно вершине xi ;
ai,j = -1 – если вершина xi является концом дуги uj,, и Г2-1 (xi,uj) = «и», если вершина xi инцидентна ребру uj .
Напомним, что предикат Г2-1 (X, U) является обратным к предикату Г2 (U, X) – «ребрам множества U инцидентны вершины множества X».
Матрицы истинности A – предиката T (X, U) и A2-1 – предиката Г2-1 (X, U) для ориентированного графа, изображенного на рисунке 15, имеет вид
|
|
|
u1
|
u2
|
u3
|
u4
|
u 5
|
|
|
|
u1
|
u2
|
u3
|
u4
|
u 5
|
|
|
|
x1
|
1
|
1
|
0
|
0
|
0
|
|
|
x1
|
0
|
0
|
0
|
0
|
0
|
|
|
A1 =
|
x2
|
-1
|
0
|
1
|
-1
|
0
|
|
A2-1 =
|
x2
|
1
|
0
|
0
|
1
|
0
|
|
|
|
x3
|
0
|
0
|
0
|
1
|
0
|
,
|
|
x3
|
0
|
0
|
0
|
0
|
0
|
.
|
|
|
x4
|
0
|
-1
|
-1
|
0
|
0
|
|
|
x4
|
0
|
1
|
1
|
0
|
1
|
|
Сопоставьте матрицы истинности предиката Г1 – A1 , предиката Г2-1 – A2-1 и матрицу A.
При указанном определении элементов матрицы А она не может быть использована для представления графов с петлями. Данный недостаток можно устранить, если элементу матрицы присваивать значение, например ±1, если uj петля при вершине xi. Такая матрица, обозначим ее через A’. для ориентированного графа, изображенного на рисунке 15, имеет вид:
|
|
|
|
|
|
|
u1
|
u2
|
u3
|
u 4
|
u 5
|
|
|
|
|
|
|
|
x1
|
1
|
1
|
0
|
0
|
0
|
|
|
|
|
|
|
|
x2
|
-1
|
0
|
1
|
-1
|
0
|
|
|
|
|
|
|
A’ =
|
x3
|
0
|
0
|
0
|
1
|
0
|
.
|
|
|
|
|
|
|
x4
|
0
|
-1
|
-1
|
0
|
±1
|
|
Аналитическое представление ориентированного графа – образами и прообразами множеств вершин и ребер относительно предикатов Г1 (X, U) и Г2 (U, X). В ориентированном графе образ вершины xiÎX относительно предиката Г1 (X, U), т. е. подмножество Ui+ Í U инцидентных ей ребер, определяется аналогично ультраграфу как характеристическое множество Г1xi предиката-свойства Г1xi (U), т. е. вектора-строки матрицы А1. Множество подмножеств ребер, инцидентных вершинам xi Î X, т. е. образ множества X относительно предиката Г1, будет
Г1X = {Г1xi / xi Î X},
где Г1xi = Ui+ = {uj Î U : Г1xi (uj) = «и» } .
В соответствии с (33) образом ребра ujÎU относительно предиката Г2 (U, X) будет одноэлементное подмножество Xj+. Образ множества ребер U относительно того же предиката будет задаваться множеством одноэлементных подмножеств Xj+ – характеристических подмножеств предикатов-свойств Г2uj(X), т. е. строк матрицы А2 :
Г2U = { Г2uj / uj Î U },
где Г2uj = Xj+= { xi Î X : Г2ui (xi) = «и» } , | Xj+| = 1.
Ориентированный граф, заданный множествами вершин X, ребер U и их образами, т. е. множествами подмножеств Г1 X и Г2 U, будем обозначать как G (X, U, Г1X, Г2U). Ориентированный граф, изображенный на рисунке 15, этим способом будет задан через:
X = {x1, x2, x3, x4}, U = {u1, u2, u3, u4, u5},
Г1 X = {Г1xi /i=1,4},
где: Г1x1 = {u1, u2}, Г1x2 = {u3}, Г1x3 = {u4}, Г1x4 = {u5},
Г2 U = { Г2uj / j = 1,5},
где: Г2u1 = {x2}, Г2u2 = {x4}, Г2u3 = {x4}, Г2u4 = {x2}, Г2u5 = {x4}.
Прообраз вершины xi, т. е. множество ребер, которым она инцидентна, является характеристическим множеством i-го вектора-строки матрицы истинности А2-1 предиката Г2-1 (X, U) или характеристическим множеством i-го вектора-столбца матрицы А2, т. е. предиката-свойства Г2xi (U) – Ui– = Г2xi.
Прообразом множества X относительно предиката Г2 (U, X) будет множество характеристических подмножеств предикатов-свойств Г2xi (U):
Г2 X = { Г2xi / xi Î X },
где Г2xi = Ui– = {uj Î U : Г2xi (uj) = «и» } .
Прообразом Г1uj ребра ujÎ U ориентированного графа относительно предиката Г1 (X, U) будет одноэлементное подмножество Xj–. Это подмножество является характеристическим множеством предиката-свойства Г1uj (X), соответствующего j-у вектору-столбцу матрицы А1.
Прообразом множества U относительно предиката Г1 (X, U) является множество характеристических подмножеств предикатов-свойств Г1u j(X):
Г1U = {Г1uj / ujÎ U },
где Г1uj = Xj– = {xi Î X : Г1ui (xi) = «и» } , | Xj– | = 1 .
У ориентированного графа, показанного на рисунке 15,
Г2X : Г2x1 = Æ, Г2x2 = {u1, u4}, Г2x3 =Æ , Г2x4 = {u2, u3, u5},
Г1U : Г1u1 = {x1}, Г1u2 = {x1}, Г1u3 = {x2}, Г1u4 = {x3}, Г1u5 = {x4}.
Для данного способа представления ориентированный граф будем обозначать G (X, U, Г1X, Г2X, Г1U, Г2U).
Предикаты смежности F1 (X, X) вершин и F2 (U, U) ребер ориентированного графа. Связь предиката смежности F1 (X, X) вершин ориентированного графа с предикатами инцидентности Г1 (X, U) и Г2 (U, X) устанавливает выражение (4). Вершины, смежные вершине xi, задаются предикатом – свойством, который определяется по формуле (5). Например, у ориентированного графа, показанного на рисунке 15, Г1x1 = {u1, u2}, характеристические вектора предикатов Г2u1 (X), Г2u2 (X) и F1x1 (X) будут:
Г2u1(X) = {0, 1, 0, 0}, Г2u2 (X) = {0, 0, 0, 1} и
F1x1(X) = Г2u1 (X) Ú Г2u2 (X) = {0, 1, 0, 1}.
Предикат-отношение смежности F1 (X, X) получается по выражению (6).
Значения элементов r1i,t (i, t = 1,n ; n = |X|) матрицы смежности R1 вершин ориентированного графа определяются по тому же правилу, что и ультраграфа. Матрица смежности R1 ориентированного графа, изображенного на рисунке 15, имеет вид:
|
|
|
0
|
1
|
0
|
1
|
|
|
|
|
0
|
0
|
0
|
1
|
|
|
R1
|
=
|
0
|
1
|
0
|
0
|
.
|
|
|
|
0
|
0
|
0
|
1
|
|
Изображение графа смежности вершин ориентированного графа без кратных ребер совпадает с его представлением, показанном на рисунке 15,а, так как истинность отношений инцидентности Г1 (X, U) и Г2 (U, X) при данном способе не отображается. Очевидно, что в графе смежности вершин ориентированного мультиграфа не будет кратных ребер.
Вершины, которым смежны вершины множества X, задает предикат F1-1 (X, X). Связь предиката F1-1 (X, X), обратного к предикату F1 (X, X), с предикатами инцидентности Г1 (X, U) и Г2 (U, X) устанавливает выражение (7). Вершины, которым смежна вершина xi, задаются предикатом – свойством F-1xi (X), определяемым по формуле (8). Например, у ориентированного графа, показанного на рисунке 15, Г2 x4 = {u2, u3, u5}, характеристические вектора предикатов Г1u2 (X), Г1u3 (X) , Г1u5 (X) и F1-1x4 (X) будут:
Г1u2 (X) = {1, 0, 0, 0}, Г1u3 (X) = {0, 1, 0, 0}, Г1u5 (X) = {0, 0, 0, 1} и
F1-1x4 (X) = Г1u2 (X) Ú Г1u3 (X) Ú Г1u5 (X) = {1, 1, 0, 1}.
Предикат-отношение смежности F1-1(X,X) получается по выражению (9).
Матрица истинности R1-1 предиката F1-1(X,X) по матрице смежности R1 в соответствии с (10) получается транспонированием последней и для графа, изображенного на рисунке 15, имеет вид:
|
|
|
0
|
0
|
0
|
0
|
|
|
|
|
1
|
0
|
1
|
1
|
|
|
R1-1
|
=
|
0
|
0
|
0
|
0
|
.
|
|
|
|
1
|
1
|
0
|
1
|
|
Смежность ребер ориентированного графа определяется так же, как и ультраграфа. Связь предиката F2 (U, U) смежности ребер ориентированного графа с предикатами инцидентности Г1 (X, U) и Г2 (U, X) устанавливает выражение (11), а предиката F2-1 (U, U) с теми же предикатами – выражение (13). С учетом (33), т. е. того факта, что в обыкновенном ориентированном графе ребру инцидентна только одна вершина и ребро инцидентно так же одной вершине, ребра, смежные ребру uj, будут определяться по формуле:
F2 uj (U) = Г1 xi (U), xi = Г2uj , (34)
а ребра, которым смежно ребро uj, – по формуле:
F2-1 uj (U) = Г2 xi (U), xi = Г1uj (35)
(сравните с выражениями (12) и (14) соответственно).
Для ребра u3 ориентированного графа, изображенного на рисунке 16:
Г2 u3 = {x1} и характеристический вектор F2 u3 (U) = Г1 x1 (U) = {1,1,0,0},
Г1 u3 = {x3} и характеристический вектор F2-1 u3 (U) = Г2 x3 (U) = {0,1,0,1}.
Предикаты-отношения смежности ребер ориентированного графа F2(U,U) и F2-1(U,U) по предикатам инцидентности Г1 и Г2 будут определяться по следующим выражениям:
F2 (U, U) = {Г1 xi (U), xi = Г2uj / uj Î U } (36)
и F2-1 (U, U) = {Г2 xi (U), xi = Г1uj / uj Î U } . (37)

Рисунок 16 – Ориентированный граф (к определению смежности вершин и ребер)
Элементы матрицы смежности R2 ребер ориентированного графа определяются по правилу:
ì 1 – если a2j,i =1 & a1i,k=1,
r2j,k = í
î 0 – в противном случае,
где j, k = 1, m; m = | U |, i = 1, n; n = | X |, a2j,i и a1i,k – элементы матриц инцидентности А2 и А1 соответственно. Матрицы инцидентности А1, А2 и смежности R2 ребер ориентированного графа, изображенного на рисунке 16, будут:
|
|
|
1
|
1
|
0
|
0
|
|
|
|
0
|
1
|
0
|
|
|
|
0
|
0
|
0
|
1
|
|
|
A1
|
=
|
0
|
0
|
0
|
1
|
,
|
A2
|
=
|
0
|
0
|
1
|
,
|
R2
|
=
|
0
|
0
|
1
|
0
|
.
|
|
|
|
0
|
0
|
1
|
0
|
|
|
|
1
|
0
|
0
|
|
|
|
1
|
1
|
0
|
0
|
|
|
|
|
|
|
|
|
|
|
|
0
|
0
|
1
|
|
|
|
0
|
0
|
1
|
0
|
|
Граф смежности G (U, U) ребер ориентированного графа, соответствующий матрице R2, показан на рисунке 17. Здесь ребра изображены кружками, а истинность F2 (uj, uk) – стрелками.

Рисунок 17 – Граф смежности ребер ориентированного графа, изображенного на рисунке 16
Матрица истинности R2-1 предиката F2-1 (U, U) на основании (15 ) получается транспонированием матрицы R2.
Образы и прообразы множеств вершин и ребер ориентированного графа относительно предикатов их смежности F1 (X, X) и F2 (U, U) соответственно. Для каждой вершины xiÎX ориентированного графа ее образ F1xi относительно предиката смежности F1(X, X) (множество смежных ей вершин Xi+) определяется характеристическим множеством предиката-свойства F1xi (X). Истинность предиката-свойства F1xi (X) задается i-м вектором-строкой матрицы R1.
Множество вершин Xi–, которым смежна вершина xi , т. е. ее прообраз F1-1xi относительно предиката F1 (X, X), является характеристическим множеством предиката-свойства F1-1xi (X) . Истинность предиката-свойства F1-1xi (X) задается i-м вектором-строкой матрицы R1-1 или соответствующим вектором-столбцом матрицы R1.
По аналитическому представлению ориентированного графа в виде G (X, U, Г1X, Г2X, Г1U, Г2U) для каждой вершины xi Î X ее образ F1xi определяется по выражению (16), а прообраз F1-1xi – по выражению (17).
Если в ориентированном графе нет кратных ребер, то с учетом (33) эти формулы упрощаются и имеют соответственно вид:
F1xi = {Г2uj / uj Î Г1 xi } (38)
и F1-1xi = {Г1uj / uj Î Г2 xi } . (39)
У ориентированного графа, изображенного на рисунке 16, на основании (38) и (39) образ вершины x1 и прообраз вершины x3 будут получены так:
Г1 x1 = {u1, u2}, Г2 u1 = {x2}, Г2 u2 = {x3}, F1 x1 = {x2 , x3};
Г2 x3 = {u2, u4}, Г1 u2 = {x1}, Г1 u4 = {x2}, F1-1x1 = {x1, x2}.
Образ и прообраз множества вершин X относительно предиката смежности F1 (X, X) будут:
F1X = {F1xi / xi Î X}
и F1-1X = {F1-1xi / xi Î X}.
Для того же ориентированного графа множества образов F1 X и прообразов F1-1 X его вершин относительно предиката смежности F1 будут:
F1 X ={F1xi /i = 1,3}: F1x1 = {x2, x3}, F1x2 = {x3}, F1x3 = {x1}; F1-1 X = {F1-1xi / i = 1,3}: F1-1x1 = {x3}, F1-1x2 = {x1}, F1 -1x3 = {x1, x2}.
Образ F2uj и прообраз F2-1uj ребра uj Î U относительно предиката F2 (U, U), т. е. множества Uj+ смежных ему ребер и Uj– ребер, которому это ребро смежно, являются характеристическими множествами предикатов-свойств F2uj (U) и F2-1uj (U) соответственно. Истинность предиката F2uj (U) задается j-м вектором-строкой матрицы R2, а истинность предиката F2-1uj (U) – j-м вектором-строкой матрицы R2‑1 или соответствующим вектором-столбцом матрицы R2.
По аналитическому представлению ориентированного графа для каждого ребра uj Î U его образ F2uj и прообраз F2-1uj определяются на основании (34) и (35) :
F2uj = Г1xi , xi = Г2uj , (40)
и F2-1uj = Г2xi , xi = Г1uj . (41)
Образ и прообраз множества ребер U относительно предиката смежности F2 (U, U) будут:
F2U = { Г1xi , xi = Г2uj / uj Î U}
и F2-1U = { Г2xi , xi = Г1uj / uj Î U}.
Для ориентированного графа, изображенного на рисунке 16, множества образов F2U и прообразов F2-1U его ребер относительно предиката смежности F2 будет:
F2U = {F2uj / j = 1,4}: F2u1 = {u4}, F2u2 = {u3}, F2u3 = { u1, u2}, F2u4 = {u3}, F2-1U = {F2-1uj / j = 1,4}: F2-1u1 = F2-1u2 = {u3}, F2-1u3 = {u2, u4}, F2-1u4 = {u1}.
Задание ориентированного графа множествами вершин X, ребер U и их образами и прообразами относительно предикатов смежности F1(X,X) и F2(U,U) соответственно будем обозначать G (X, U, F1X, F1-1X, F2U, F2-1U) .
Отметим в заключение, что представление ориентированного графа через предикаты смежности вершин и ребер задает его не полностью.
Характеристики вершин и ребер ориентированного графа. К характеристикам вершин относятся:
· r+ (xi) – полустепень исхода, т. е. количество ребер, инцидентных вершине xi Î X;
· r- (xi) – полустепень захода, т. е. количество ребер, которым инцидентна вершина xi Î X.
По матрицам инцидентности A1 и A2 , а также при аналитическом представлении ориентированного графа эти показатели рассчитываются по тем же формулам, что и для ультраграфа.
Для графа, изображенного на рисунке 16, полустепень исхода вершины x1 по матрице A1 будет
4
r+(x1) = S a11,j =2
j=1
и вершины x2 по аналитическому представлению r+(x2) = | Г1x2 |=1;
полустепень захода вершин x3 и x1 по матрице A2 и по аналитическому представлению соответственно –
4
r-(x3) = S a2j,3 = 2 и r-(x1) = | Г2x1 | =1;
j=1
· s+ (xi) – количество вершин, смежных вершине xi Î X ;
· s- (xi)– количество вершин, которым смежна вершина xi Î X.
Эти показатели имеют смысл только для мультиграфа, так как для графа без кратных ребер они совпадают с полустепенями исхода и захода соответственно. По матрицам смежности R1 и R1-1 и при известных образах и прообразах вершин относительно предиката смежности F1(X,X) эти показатели рассчитываются по тем же формулам, что и для ультраграфа.
Для вершины x1 ориентированного графа, показанного на рисунке 18, r+ (x1) = 3, а s+ (x1) = 2 и r- (x1) = 1, а s- (x1) = 1;
· e(xi) = |{uj Î U : Г1uj = Г2uj = xi}| – количество петель при вершине xi.

Рисунок 18 – Ориентированный мультиграф
Характеристики ребер ориентированного графа:
· s+(uj)– количество ребер, смежных ребру ujÎU;
· s-(uj)– количество ребер, которым смежно ребро ujÎU.
По матрицам смежности R2 или R2-1и при известных образах и прообразах ребер относительно предиката смежности F2(U,U) эти показатели рассчитываются по тем же формулам, что и для ультраграфа.
Например, для ребер u3 и u1 ориентированного графа, показанного на рисунке 16,
4 4
s+(u3) = S r23,j = 2 и s-(u1) = S r2i,1 = 1 или
j=1 i=1
s+(u3) = | F2u3 |=2 и s-( u1) = | F2-1u1| = 1.
Если образы и прообразы ребер относительно предиката смежности F2 (U, U) не заданы, эти показатели при известных образах Г1X множества вершин X относительно предиката Г1 (X, U) и прообразах Г2X относительно предиката Г2 (U, X), а также образах и прообразах множества ребер относительно соответствующих предикатов, на основании (38) и (39) будут определяться по формулам:
s+(uj) = | Г1xi |, xi = Г2 uj и s-(uj) = | Г2xi |, xi = Г1 uj .
Обыкновенные неориентированные графы. Данный вид графа можно определить как два непересекающихся множества вершин X и ребер U, на элементах которых задана пара двуместных предикатов-отношений инцидентности Г1 (X, U) и Г2 (U, X), удовлетворяющих условиям (1), (20) и выражению:
" uj Î U (|Г1uj| = |Г2uj| = 2).
Таким образом ребра обыкновенного неориентированного графа соединяют вершины попарно, а предикат Г2 (U, X) на основании (20) является обратным к предикату Г1 (X, U). Обыкновенный неориентированный граф будет задан, если заданы множества X, U и один из этих предикатов. Из сказанного выше следует, что он является частным случаем гиперграфа. Изображение неориентированного графа дано на рисунке 19.

Рисунок 19 – Неориентированный граф (а) и мультиграф (б)
Представление неориентированного графа матрицей инцидентности. Так как матрица предиката Г2 (U, X) является транспонированной матрицей предиката Г1 (X, U), для матричного представления неориентированного графа достаточно одной из них. В качестве матрицы инцидентности A будем использовать матрицу истинности предиката Г1 (X, U), размером n´m, где n = |X|, а m = |U|. Элементы этой матрицы определяются по тому же правилу, что и для гиперграфа.
Матрица инцидентности графа, показанного на рисунке 19,б, имеет вид
|
|
|
u1
|
u2
|
u3
|
u4
|
u5
|
u6
|
|
|
|
x1
|
1
|
0
|
0
|
0
|
0
|
0
|
|
|
A =
|
x2
|
1
|
1
|
1
|
0
|
1
|
0
|
|
|
|
x3
|
0
|
0
|
1
|
1
|
1
|
1
|
.
|
|
|
x4
|
0
|
1
|
0
|
1
|
0
|
0
|
|
Представление неориентированного графа образами вершин и ребер относительно предикатов Г1 (X, U) и Г2 (U, X). В неориентированном графе образ Г1xi вершины xiÎX относительно предиката Г1 (X, U) является характеристическим множеством предиката-свойства Г1xi (U), т. е. вектора-строки матрицы А. Множество подмножеств ребер, инцидентных вершинам xi Î X, т. е. образ множества X относительно указанного предиката, определяется по выражениям (23).
Образ множества ребер U относительно предиката Г2 (U,X), т. е. множество подмножеств Г2uj, будет задаваться множеством характеристических подмножеств предикатов-свойств Г2uj (X), т. е. столбцов матрицы А и определяется по выражениям (24). На основании (20) и (33) количество вершин, инцидентных каждому ребру неориентированного графа без петель, | Г2uj | = 2.
Неориентированный граф данным способом будет задан, если заданы множества вершин X, ребер U и их образы, т. е. множества подмножеств Г1X и Г2U. Граф в данном случае будем обозначать как G (X, U, Г1X, Г2U). Неориентированный граф, изображенный на рисунке 19,б, этим способом будет представлен:
X = {x1, x2, x3, x4}, U={u1, u2, u3, u4, u5, u6},
Г1X = {Г1xi /i = 1,4},
где: Г1x1 = {u1}, Г1x2 = {u1, u2, u3, u5}, Г1x3 = {u1, u4, u5, u6}, Г1x4 = { u2, u4},
Г2U={ Г2uj / j=1,6},
где: Г2u1 = { x1, x2}, Г2u2 = { x2, x4}, Г2u3 = { x2, x3}, Г2u4 = { x3, x4}, Г2u5 = { x2, x3}, Г2u6 = {x3}.
Рассмотренное представление неориентированного графа, так же как и матричное, является полным.
Предикаты смежности F1(X,X) вершин и F2(U,U) ребер неориентированного графа. Для вершин xi, xk ÎX связь предиката смежности F1 (X, X) с предикатами Г1 (X, U) и Г2(U, X) определяется выражением (25).
Инцидентные вершине xi ребра задает характеристическое множество Ui = Г1xi предиката-свойства Г1xi (U). Вершины, инцидентные ребру uj Î Ui , определяет предикат-свойство Г2uj (X). Если uj не является петлей, подмножество Г2uj состоит из двух вершин, одна из которых xi (смотри первые пять столбцов матрицы А).Таким образом, вершины, смежные вершине xi, будут задаваться предикатом – свойством, определяемым по выражению (26).
У графа, показанного на рисунке 19,б, U2 = Г1x2 = {u1, u2, u3, u5} и характеристические вектора предикатов Г2u1 (X), Г2u2 (X), Г2u3 (X), Г2u5 (X) равны:
Гu1 (X) ={1,1,0,0}, Гu2 (X) = {0,1,0,1}, Гu3 (X) = {0,1,1,0}, Гu5 (X) = {0,1,1,0}.
После присваивания Г2u1 (x2), Г2u2 (x2), Г2u3(x2) и Г2u5 (x2) значения «0» получаем
F1x2 (X) = Г2u1 (X) Ú Г2u2 (X) Ú Г2u3 (X) Ú Г2u5 (X) ={1,0,1,1},т. е. вершина x2 смежна вершинам x1, x3, x4.
Предикат-отношение F1 (X, X) смежности вершин неориентированного графа определяется выражением (27).
Матрица истинности этого предиката является матрицей смежности вершин неориентированного графа. Элементы этой матрицы по матрице инцидентности А определяются по тому же правилу, что и для гиперграфа.
Матрицы смежности R1 и R1¢, вершин графов, изображенных на рисунках 19,а и б, будут иметь вид:
|
|
|
0
|
1
|
0
|
0
|
|
|
|
0
|
1
|
0
|
0
|
|
|
R1
|
=
|
1
|
0
|
1
|
1
|
,
|
R1¢
|
=
|
1
|
0
|
1
|
1
|
.
|
|
|
|
0
|
1
|
0
|
1
|
|
|
|
0
|
1
|
1
|
1
|
|
|
|
|
0
|
1
|
1
|
0
|
|
|
|
0
|
1
|
1
|
0
|
|
В соответствии со свойством (20) матрицы симметричны относительно главной диагонали. Изображение графа смежности вершин неориентированного графа, показанного на рисунке 19,а, имеет тот же вид, а для мультиграфа, представленного на рисунке 19,б, отличается отсутствием кратных ребер.
Для ребер uj, ur Î U связь предиката смежности F2 (U, U) с предикатами Г2 (U, X) и Г1 (X, U) определяется выражением (26). Вершины, инцидентные ребру ujÎU, задает характеристическое множество Xj = Г2uj предиката-свойства Г2uj (X). Ребра, инцидентные вершине xiÎX, определяет предикат-свойство Г1xi (U). Подставляя в Г1 (X, U) вершины множества Xj (| Xj | = 2), получаем пару предикатов-свойств {Г1xi (U)}, xi Î Xj, каждый из которых задает ребра, смежные ребру uj по вершине xi. Предикат-свойство F2uj (U), задающий ребра, смежные ребру ujÎU в неориентированном графе, определяется по выражению (29).
У графа, показанного на рисунке 19,б, Г2u1 = {x1, x2} и характеристические вектора предикатов Г1x1(U) и Г1x2(U) имеют значения:
Г1x1 (U) ={1, 0, 0, 0, 0, 0} и Г1x2 (U) = {1, 1, 1, 0, 1, 0}.
Так как |Г2u1| = 2, присваиваем Г1x1( u1) и Г1x2( u1) значения «0» и получаем
F2u1(U) = {0, 0, 0, 0, 0, 0}Ú {0, 1, 1, 0, 1, 0} = {0, 1, 1, 0, 1, 0}, т. е. ребро u1 смежно ребрам u2, u3 и u5.
Предикат-отношение F2 (U, U) смежности ребер неориентированного графа определяет выражение (30). Элементы матрицы смежности ребер R2 по матрице инцидентности А определяются по тому же правилу, что и гиперграфа. Матрица смежности ребер неориентированного мультиграфа, изображенного на рисунке 19,б, имеет вид:
|
|
|
0
|
1
|
1
|
0
|
1
|
0
|
|
|
|
|
1
|
0
|
1
|
1
|
1
|
0
|
|
|
R2
|
=
|
1
|
1
|
0
|
1
|
1
|
1
|
.
|
|
|
|
0
|
1
|
1
|
0
|
1
|
1
|
|
|
|
|
1
|
1
|
1
|
1
|
0
|
1
|
|
|
|
|
0
|
0
|
1
|
1
|
1
|
1
|
|
Граф смежности ребер этого же графа представлен на рисунке 20.
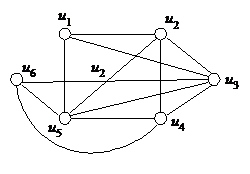
Рисунок 20 – Граф смежности ребер графа, изображенного на рисунке 19,б
Здесь ребра неориентированного графа изображены кружками, а истинность F2(uj, ur) – линиями.
Образы множеств X и U относительно предикатов смежности вершин F1 (X, X) и ребер F2 (U, U) соответственно. Для каждой вершины xi Î X неориентированного графа G (X, U) множество смежных ей вершин Xi = F1xi определяется характеристическим множеством предиката-свойства F1xi (X), истинность которого задается i-м вектором-строкой матрицы R1.
По аналитическому представлению графа в форме G(X, U, Г1X, Г2U) для каждой вершины xi Î X ее образ Fxi на основании (26) определяется по правилу (31). Для неориентированного графа без кратных ребер формула упрощается и имеет вид:
F1xi = { Г2uj \ xi : | Г2uj | = 2 Ú Г2uj : | Г2uj | = 1 / uj Î Г1xi }. (42)
Для графа, изображенного на рисунке 19,а, множество ребер, инцидентных вершине x2, т. е. ее образ относительно предиката Г1(X, U), – Г1x2 ={u1, u2, u3} и образы каждого из этих ребер относительно предиката Г2(U, X) будут: Г2u1={x1, x2}, Г2u2={x2, x4}, Г2u3={x2, x3}. Исключив из Г2uj вершину x2, получим F1x2 ={x1, x4, x3}.
Множество образов F1X ={ F1xi / xiÎ X } вершин этого графа относительно предиката смежности F1(X,X) будет:
F1X = {F1xi /i =1,4}:
F1x1 = {x2}, F1x2 ={x1, x4, x3}, F1x3 = {x2, x4}, F1x4 = {x2, x3}.
Для каждого ребра uj Î U неориентированного графа G (X, U) множество смежных ему ребер Uj = F2uj определяется характеристическим множеством предиката-свойства F2uj (U), истинность которого задается j-м вектором-строкой матрицы R2.
По аналитическому представлению графа образ ребра F2uj на основании (32) определяется по правилу
F2uj = {Г1xi \ uj : | Г2uj | = 2 Ú Г1xi : | Г2uj | = 1 / xi Î Г2uj}. (43)
Для графа, изображенного на рисунке 19,а, множество вершин, инцидентных ребру u2, т. е. его образ относительно предиката Г2(U, X) – Г2u2 ={x2, x4} и образы каждой из этих вершин относительно предиката Г1(X, U) будут: Г1x2={u1, u2, u3}, Г1x4={u2, u4}. Исключив из Г1xi ребро u2, получим F2u2 ={u1, u3, u4}.
Множество образов F2U = { F2uj / ujÎ U } ребер этого графа относительно предиката смежности F2(U,U) будет:
F2U = {F2uj /i =1,4}:
F2u1 = {u2, u3}, F2u2 ={u1, u3, u4}, F2u3 ={u1, u2, u4}, F2u4 = {u2, u3}.
Аналитическое представление неориентированного графа множествами вершин X, ребер U и их образами относительно предикатов смежности F1(X, X) и F2(U, U) соответственно будем обозначать G (X, U, F1X, F2U).
Задание неориентированного графа только через предикаты смежности вершин и ребер является неполным.
Характеристики вершин и ребер неориентированного графа. К характеристикам вершин относятся:
· r(xi) – локальная степень вершины, т. е. количество ребер, инцидентных вершине xi Î X.
По матрице инцидентности A , а также при аналитическом представлении неориентированного графа этот показатель рассчитывается по тем же формулам, что и для гиперграфа.
Для графа, изображенного на рисунке 19,б, локальная степень вершины x2 по матрице A будет
6
r(x2) = Sa2, j =4
j=1
и вершины x4 по аналитическому представлению –
r(x4) = | Г1x4 |=2;
· s(xi) – количество вершин, смежных вершине xiÎX. Этот показатель имеет смысл только для мультиграфа, так как для графа без кратных ребер он совпадает с локальной степенью. По матрице смежности R1 и при известных образах вершин относительно предиката смежности F1(X,X) этот показатель определяется по тем же формулам, что и для гиперграфа.
4
Для вершины x2 того же графа s(x2) = Sr12, j =3 – сравните с s(x3) =4.
j=1
· e(xi) – количество петель при вершине xi. По матрице инцидентности A и при аналитическом представлении характеристика определяется по тем же выражениям, что и для гиперграфа.
Характеристики ребер неориентированного графа:
· s(uj)– количество ребер, смежных ребру ujÎU.
По матрице смежности R2 и при известных образах ребер относительно предиката смежности F2 (U, U) этот показатель рассчитывается по тем же формулам, что и для гиперграфа.
Например, для ребер u3 и u1 неориентированного мультиграфа, показанного на рисунке 19,б,
6
s(u3) =S r23,j =5 и для ребра u1 графа, изображенного на рисунке 19,а,
j=1
s ( u1) = | F2u1| = 2.
Литература
1. Овчинников В.А. Автоматизация комбинаторно‑оптимизацион-ных задач при проектировании ЭВМ и систем: Учеб. для вузов. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2001.
Публикации с ключевыми словами: структурный синтез
Публикации со словами: структурный синтез
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



