научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 01, январь 2009
УДК 621.771.014
МГТУ им. Н.Э. Баумана, Москва
avoskan@bmstu.ru
Введение
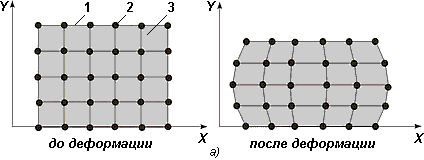
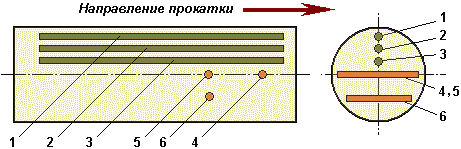
Современные теоретические исследования процессов обработки металлов давлением (ОМД) в значительной степени базируются на численных методах анализа [1…3], наиболее эффективным из которых является метод конечных элементов (МКЭ) [4, 5]. Как правило, исследование технологических процессов ОМД проводится на конечно-элементных моделях, описывающих движение сплошной среды на основе подхода Лагранжа. При этом объем деформируемой заготовки разбивается на элементарные объемы, образующие сетку лагранжевых конечных элементов (КЭ), узлы которой принадлежат материалу заготовки. При деформации заготовки лагранжевы КЭ деформируются и перемещаются вместе с материалом (рис. 1, a). В этом случае разрешающие уравнения сплошной среды записываются для узлов КЭ модели. Такая постановка задачи дает преимущества в исследовании изменения параметров модели во времени. Достаточно просто, например, можно учесть в лагранжевой модели изменение физических свойств материала в процессе ОМД.
Авторами был выполнен ряд работ по моделированию процессов прокатки на основе лагранжевых сеток КЭ в среде комплекса МКЭ-анализа ANSYS. В частности, исследовалась поперечно-винтовая прокатка на стане ПВП 20-60 (рис. 3). Полученные на лагранжевых моделях поля распределения напряжений хорошо корреспондировались с результатами исследований А.И. Целикова, А.Д. Томленова, П.К. Тетерина и др. Величины энергосиловых параметров прокатки, полученные при моделировании, были близки к реальным данным по стану ПВП 20-60 [6, 7].
В то же время, опыт моделирования различных технологических задач ОМД с развитым течением металла в подвижном очаге деформации с помощью лагранжевых сеток показал, что в ряде случаев имеет место несоответствие теоретических и практических результатов, касающихся, как правило, формоизменения заготовки [8]. Известны, например, экспериментальные данные по поперечно-винтовой прокатке (ПВП) реальных заготовок, начиненных продольными штифтами-вставками, находящимися на различном расстоянии от оси заготовки. При этом наблюдалась "завивка" штифтов по спирали с шагом, не зависящим от местоположения штифта (рис. 4) [9, 10]. В результате был сделан вывод о том, что, в процессе ПВП наблюдается сложное течение металла с явлениями массопереноса, при котором волокна материала приобретают ориентированную структуру.
|
|
|
|
Рис. 3. Некоторые результаты моделирования холодной поперечно-винтовой прокатки на основе подхода Лагранжа, представленные в работах [6, 7]
|
Рис. 4. Деформация при ПВП внедренных в заготовку продольных штифтов [10]. Цилиндрическая заготовка со штифтами проточена после прокатки по радиусам расположения штифтов
|
Однако при МКЭ-моделировании данного процесса на основе лагранжевых сеток спиральной "завивки" вставных элементов получить не удалось [7]. Кроме того, глубина "воронки", образующейся на переднем конце заготовки при ПВП в трех валках, по даннным МКЭ-моделирования не превышала величины 0,05...0,1 исходного диаметра заготовки (рис. 3), в то время как глубина "воронки" на реальных прокатанных образцах может достигать величины 1…1,5 диаметра. Так, например, при поперечно-винтовой 3-валковой прокатке заготовки из алюминиевого сплава с диаметра D = 70 мм на диаметр d = 37 мм (вытяжка λ = 3,58) глубина "воронки" составляла примерно 65 мм (рис. 5). При этом на переднем конце прокатанного прутка наблюдалась существенная неравномерность и несимметричность деформации металла.
Таким образом, опыт применения лагранжевых сеток при анализе процессов, характеризующихся большими деформациями, показал невозможность получения достоверных результатов по формоизменению заготовки вследствие искажения и вырождения КЭ-сетки. Это обстоятельство явилось основанием к поиску альтернативного метода решения технологических задач ОМД, характеризующихся большими деформациями металла.
|
|
|
|
Рис. 5. Заготовка ("недокат") из алюминия, прокатанная методом ПВП в 3-х валках. Хорошо видна "воронка" на переднем конце заготовки. Отвертка на фото наглядно демонстрирует ее глубину
|
|
Помимо подхода Лагранжа в изучении поведения сплошной деформируемой среды существует подход Эйлера, при котором объектом изучения являются различные поля, характеризующие движение сплошной среды. В отличие от лагранжевой постановки, при подходе Эйлера исследуется неподвижное пространство наблюдателя, заполненное движущейся средой (средами). В этом случае эйлерова сетка КЭ модели остается неизменной во времени и не искажается вместе с материалом, так как узлы эйлеровой сетки суть фиксированные точки пространства (см. рис. 1, б). При этом каждый КЭ эйлеровой сетки в конкретный момент времени может обладать свойствами той или иной материальной среды (в частности, свойствами материала деформируемой заготовки), либо принадлежать пустому пространству.
В ходе решения рассматривается движение деформируемой сплошной среды (или нескольких различных сред) внутри эйлеровой сетки КЭ. В результате становится возможным решить проблему больших деформаций и учесть явления массопереноса. Таким образом, эйлерова постановка МКЭ целесообразна при моделировании технологических процессов ОМД, для которых характерны большие пластические деформации. Вместе с тем, при описании технологического инструмента в КЭ-моделях процессов ОМД применение сеток Эйлера нецелесообразно в силу малых деформаций инструмента (часто инструмент рассматривают как абсолютно жесткий), поэтому КЭ-модели инструмента имеет смысл строить на основе сеток Лагранжа.
В вычислительном аспекте реализация подхода Эйлера существенно осложнена, поскольку помимо КЭ моделей деформируемой заготовки и технологического инструмента в этом случае приходится рассматривать модель некоторого объема пространства, в котором ожидается деформация металла, а также моделировать контактное взаимодействие между лагранжевыми и эйлеровыми элементами. Все эти условия приводят к увеличению размерности задачи и, как следствие, к ее усложнению.
Конечноэлементная модель процесса ПВП в постановке Эйлера
Анализ появившихся в последние годы публикаций, посвященных эйлеровому описанию процессов ОМД, показывает, что достаточно большое число работ в этой области выполнено специалистами с использованием программного комплекса ANSYS/LS-DYNA, встроенные функции которого позволяют эффективно реализовать в КЭ-модели взаимодействие лагранжевых и эйлеровых сеток. Авторами выполнено в среде ANSYS/LS-DYNA трехмерное конечноэлементное моделирование ПВП сплошной заготовки на основе эйлерова описания поведения сплошной среды.
Исследовалась холодная ПВП сплошной медной заготовки с диаметра D = 120 мм на диаметр d = 69 мм (вытяжка λ = 3) в трех валках с безгребневой калибровкой на стане ПВП 20-60 (рис. 6, а) [11]. Угол подачи был принят равным α = 9°; угол раскатки – β = 0°. В качестве материала заготовки рассматривалась медь марки М0. Это позволило использовать для описания поведения материала при деформировании билинейную изотропную упругопластическую модель [7] со следующими механическими характеристиками: предел текучести σт = 120 МПа; модуль упругости первого рода Е = 100000 МПа; модуль упрочнения Еy = 50 МПа; коэффициент Пуассона μ = 0,31; плотность ρ = 8100 кг/м3 [7]. Частота вращения валков в модели была принята постоянной и равной 60 об/мин. [11].
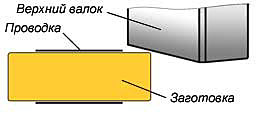
Эйлерова модель заготовки и пространства, в котором исследовалось течение металла, была сформирована из трехмерных твердотельных гексаэдрических элементов (рис. 6, б). Для стабилизации пространственного положения заготовки во время прокатки предусмотрена трубчатая проводка диаметром 130 мм (рис. 6, а). Проводка и прокатные валки моделировались в лагранжевой постановке с помощью абсолютно жестких оболочечных элементов (рис. 6, б). Валки и проводка, описанные лагранжевой КЭ-сеткой контактируют с эйлеровой КЭ-моделью заготовки. Для описания взаимодействия проводки и валков с эйлеровой средой были использованы встроенные возможности LS-DYNA. Коэффициент трения в контакте "валок-заготовка" и "заготовка-проводка" был принят равным f = 0,2 [12].
|
а)
|
б)
|
|
Рис. 6. Геометрическая (а) и конечноэлементная (б) модели процесса ПВП. 1 – валок; 2 – заготовка; 3 – проводка; 4 – пространство Эйлера
|
|
На начальной стадии прокатки (примерно 0,25 оборота валка от момента соприкосновения валка с торцем заготовки) для задания заготовки в валки используется задний подпор силой 120 кН. Силу подпора прикладывали в виде распределенной нагрузки к узлам конечноэлементной сетки, расположенным на заднем торце заготовки.
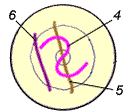
Для изучения характера течения металла по аналогии с экспериментальными исследованиями [10] в КЭ-модели была смоделирована деформация 3-х продольных и 3-х поперечных штифтов-вставок, "вмороженных" в материал заготовки (рис. 7). Штифты моделировались балочными конечными элементами и имели одинаковые механические характеристики с материалом заготовки. Общее число конечных элементов модели – 25338, число узлов – 23888.
При моделировании были приняты следующие допущения:
- исследовалась холодная прокатка (температура металла ниже температуры рекристаллизации), при этом условия деформации полагали изотермическими, что позволило не учитывать зависимость сопротивления деформации от скорости деформации; проводка и валки рассматривались как абсолютно жесткие тела;
- полагали, что трение в контакте между заготовкой и валками, а также между заготовкой и проводкой подчиняется закону сухого трения Амонтона-Кулона, причем коэффициент трения постоянен на всей контактной поверхности;
- в расчете не учитывали зависимость внутренней энергии деформируемого металла от параметров процесса (давления, температуры, изменения объема), т.е. не рассматривались уравнения состояния деформируемой среды.
Моделирование было выполнено для интервала времени t = 0...3 с, что соответствует 3-м полным оборотам валков.
|
|
Рис. 7. Размещение моделей штифтов-вставок в КЭ-модели заготовки и их нумерация: 1…3 – продольные штифты; 4…6 – поперечные штифты
|
Анализ полученных результатов
Наиболее наглядно результаты моделирования процесса ПВП иллюстрирует созданная на их основе анимация, представленная на рис. 8. Характерно, что в отличие от решения задачи на лагранжевой сетке (см. рис. 3), на переднем конце прокатанной заготовки, как и в реальном эксперименте, наблюдается существенная неравномерность и несимметричность деформации металла, а также образование "воронки" (процесс формирования "воронки" хорошо виден на рис. 8, б).
|
|
|
|
|
Рис 8. Результаты расчета процесса ПВП на эйлеровой КЭ-модели: а – формоизменение заготовки в ходе прокатки; б – деформация внедренных в заготовку штифтов
|
||
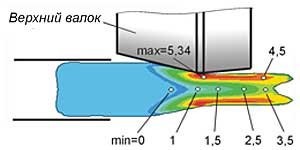
Глубина "воронки" при решении задачи в эйлеровой постановке составила ~60 мм (50% от начального диаметра заготовки) в отличие от решения в лагранжевой постановке (см. рис. 3), когда глубина "воронки" равнялась ~2,5 мм (2% от исходного диаметра заготовки). Стадии образования "воронки" и формоизменения модели заготовки во времени показаны на рис. 9.
 а) |
 б) |
 в) |
 г) |
 д) |
 е) |
|
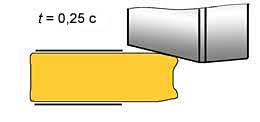
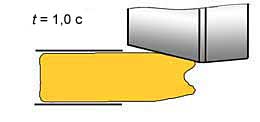
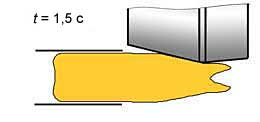
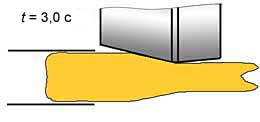
Рис. 9. Осевое продольное сечение модели заготовки во время захвата (а, б), при формировании переднего конца заготовки (в…д) и при установившемся процессе ПВП (е)
|
|
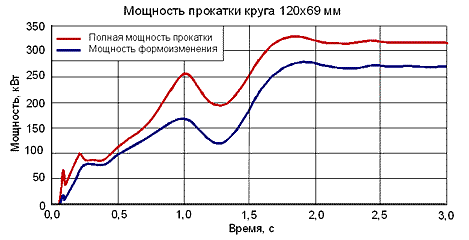
На основе результатов моделирования был проведен анализ энергозатрат процесса ПВП. На рис. 10 представлены графики изменения полной мощности ПВП и мощности формоизменения, полученные на КЭ-модели в эйлеровой постановке. На графиках можно выделить несколько характерных временных интервалов, в пределах которых наблюдается появление локальных экстремумов расчетных значений мощности формоизменения и полной мощности прокатки.
Первый экстремум полной мощности (~100 кВт) наблюдается через 0,2…0,3 с после начала захвата заготовки, в момент, предшествующий отключению подпора. Сброс силы подпора влечет кратковременное падение полной мощности до ~87 кВт. Следует отметить, что мощность прокатки при наличии силы подпора больше, чем при ПВП без подпора и натяжения. Точно такие же результаты были получены в [7] при исследовании процесса ПВП на основе лагранжевой постановки задачи МКЭ-анализа. Формоизменение заготовки в этот промежуток времени показано на рис. 9, б.
В течение последующих 0,7…0,8 с наблюдается рост мощности прокатки от 100 до 255 кВт. Рост мощности обусловлен развитием процесса захвата заготовки валками, когда основная энергия деформации расходуется на проработку переднего конца заготовки. При этом наблюдается зарождение и развитие "воронки". Продольное сечение заготовки в момент времени t ≈ 1 с показано на рис. 9, в.
 |
|
Рис. 10. Расчетные значения полной мощности прокатки и мощности формоизменения заготовки, полученные на КЭ-модели
|
Падение мощности прокатки от 255 кВт до 194 кВт в последующие 0,25 с связано с прокаткой преимущественно наружных слоев материала заготовки, из которых формируется "воронка". Можно сказать, что на данном этапе осуществляется ПВП пустотелого цилиндра (рис. 9, г). Максимального значения (~330 кВт) мощность прокатки достигает при t ≈ 1,75 с (рис. 10). К этому времени заканчивается формирование переднего конца заготовки и начинается устойчивый, стационарный режим ПВП сплошной заготовки, для которого мощность прокатки ≈ 320 кВт.
Сопоставление результатов анализа процесса ПВП на основе подхода Эйлера с полученными ранее результатами решения этой задачи на основе подхода Лагранжа [7] показало, что несмотря на различие в характере изменения мощности на начальной стадии прокатки, данные по полной мощности ПВП и энергии деформирования в установившемся режиме в обоих случаях идентичны.
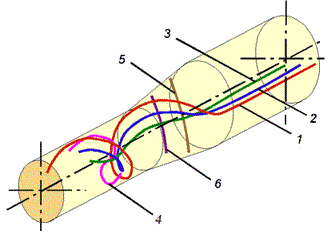
Как было отмечено ранее, течение металла и массоперенос при ПВП оценивались по деформации моделей продольных и поперечных штифтов, размещенных в заготовке (см. рис. 7). Анимация на рис. 8, б наглядно демонстритует "завивку" продольных штифтов, полученную на модели. Подробно формоизменение продольных и поперечных штифтов по результатам расчета представлено на рис. 11 и рис. 12. Номера деформированных штифтов-вставок на рис. 11, 12 соответствуют номерам штифтов на рис. 7.
|
а)
|
|
б)
|
в)
|
|
|
Рис. 11. Вид штифтов-вставок после ПВП по результатам моделирования на основе эйлеровой постановки МКЭ (1…6 – номера штифтов-вставок в соответствии с рис. 7)
|
Рис. 12. Деформация продольных (а, б) и поперечных (в) штифтов-вставок по результатам моделирования ПВП (1…6 – номера штифтов в соответствии с рис. 7)
|
|
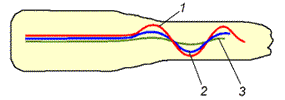
Анализ полученных данных показал, что результаты расчета практически совпадают с результатами реального физического эксперимента [10]. Как видно из рис. 12, а, деформация продольных штифтов, размещенных на различном расстоянии от оси заготовки, происходит по спирали с постоянным шагом, не зависящим от местоположения штифта. По деформации продольных и поперечных штифтов (см. рис. 11 и рис 12, б, в) можно сказать, что внешние слои металла деформируются более интенсивно и "обгоняют" внутренние, как по направлению вращения, так и в осевом направлении движения заготовки. При этом завивка штифтов начинается не сразу, как только элементарный объем металла попадает в очаг деформации, а с некоторым запаздыванием (см. рис. 12, а).
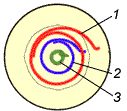
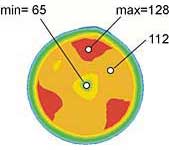
Объяснить подобное явление можно тем, что в начале очага деформации металл внутри заготовки, в отличие от поверхностных слоев, деформируется упруго. Подтверждением может служить картина распределения эквивалентных (по Мизесу) напряжений в теле заготовки (рис. 13). Из рис. 13 видно, что эквивалентные напряжения на входе в очаг деформации достигают величин напряжений текучести (~120 МПа) только в месте контакта валков с металлом (рис. 13, б, в). При этом в центре заготовки металл деформируется упруго, напряжения в нем не превышают величины ~65 МПа (рис. 13, в).
а)
|
б)
|

в)
|
|
Рис. 13. Поля эквивалентных (по Мизесу) напряжений (МПа) в момент времени t = 3 с в продольном сечении заготовки (а), в поперечном сечении на входе в очаг деформации (б) и в поперечном сечении на выходе из очага деформации (в)
|
||
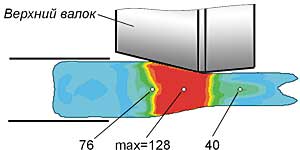
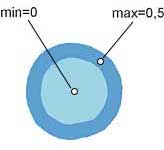
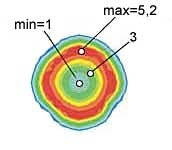
Представленные на рис. 14 поля распределения эквивалентной накопленной пластической деформации также подтверждают этот вывод. В приконтактных зонах величина накопленной пластической деформации достигает ~4,5 (рис. 14, а, б), а в центральной части заготовки она практически равна нулю, причем эта область простирается вдоль оси заготовки почти до зоны максимального обжатия (рис. 14, в). По мере прокатки напряжения текучести постепенно распространяются на всю глубину заготовки так, что на выходе из очага деформации, в зоне максимального обжатия, пластическое течение уже распространяется на все поперечное сечение прокатанной заготовки. При этом напряжения достигают своей максимальной величины ~128 МПа (рис. 13, а, в).
В подтверждение сделанного на основе анализа деформации штифтов заключения о том, что внешние слои металла смещаются более интенсивно, чем внутренние, говорит и то, что степень накопленной пластической деформации в прокатанной заготовке меняется от 1 в центре заготовки до 5,34 на внешних слоях металла прокатанного прутка.
а)
|
б)
|
в)
|
|
Рис. 14. Распределение эквивалентных (по Мизесу) деформаций в момент времени t = 3 с в продольном сечении заготовки (а), в поперечном сечении на входе в очаг деформации (б) и в поперечном сечении на выходе из очага деформации (в)
|
||
Заключение
В результате моделирования были определены поля напряжений и деформаций в прокатываемой заготовке, а также энергосиловые параметры прокатки. Установлено, что при решении задачи как в лагранжевой, так и в эйлеровой постановках расчетные величины энергосиловых параметров ПВП хорошо коррелируются с практическими результатами. Применение эйлеровой постановки задачи моделирования позволило получить достоверные результаты по формоизменению заготовки. Характер деформации штифтов-вставок, формоизменение металла и величина образовавшейся на переднем конце заготовки "воронки", полученные при эйлеровом МКЭ-моделировании практически полностью соответствуют результатам реального физического эксперимента.
- Малинин Н.Н. Технологические задачи пластичности и ползучести. – М.: Высшая школа, 1979. – 118 с.
- Целиков А.И., Белянинов В.К., Калмыков В.В. Объемные задачи теории прокатки // Труды МВТУ. – 1984. – ╧ 412. – Машины и агрегаты металлургического производства. – С.8 – 24.
- Калмыков В.В., Ананьев И.Н., Байрамов О.Ф. Расчет энергосиловых параметров и формоизменения при прокатке в черновых клетях широкополосных станов методом конечных элементов // Труды МВТУ. – 1984. – ╧ 412. – Машины и агрегаты металлургического производства. – С.57 – 67.
- Зенкевич О. Метод конечных элементов в технике: Пер. с англ. – М.: Мир, 1975. – 542 с.
- Сегерлинд Л. Применение метода конечных элементов: Пер. с англ. – М.: Мир, 1979. – 480 с.
- Восканьянц А.А., Иванов А.В. Моделирование процесса холодной поперечно-винтовой прокатки методом конечных элементов // Производство проката. – 2004. -- ╧11. – С.10 -- 17.
- Восканьянц А.А., Иванов А.В. Исследование процесса холодной поперечно-винтовой прокатки на трехмерной конечно-элементной модели // Сборник трудов Всероссийской научно-технической конференции, посвященной 100-летию со дня рождения академика А.И. Целикова (Москва, 14-15 апреля 2004 г.). / Под. ред. А.А. Восканьянца. – М.: МГТУ им. Н.Э.Баумана, 2004. – С. 332–340.
- Колмогоров В.Л. Численное моделирование больших пластических деформаций и разрушения металлов // Кузнечно-штамповочное производство, 2003, ╧2. – С. 4-16.
- Сопротивление деформации и пластичность металлов (при обработке давлением) / В.С. Смирнов, А.К. Григорьев, В.П. Пакудин, Б.В. Садовников. – М.: Металлургия, 1975. – 272 с.
- Панов Е.И., Осадчий В.Я. Особенности технологического процесса производства прутков и бесшовных труб методом поперечно-винтовой прокатки из труднодеформируемых заэвтектических силуминовых сплавов 01390 и 01391 // Сборник трудов Всероссийской научно-технической конференции, посвященной 100-летию со дня рождения академика А.И. Целикова (Москва, 14-15 апреля 2004 г.). / Под. ред. А.А. Восканьянца. – М.: МГТУ им. Н.Э.Баумана, 2004. – С. 83–94.
- Ильин О.Ю., Панов Е.И., Шапиро В.Я. Разработка конструкции оборудования и освоение поперечно-винтовой прокатки легких сплавов // Технология легких сплавов. – 2000. – ╧5. – С. 39–46.
- Целиков А.И., Никитин Г.С., Рокотян С.Е. Теория продольной прокатки. – М.: Металлургия, 1980. – 320 с.
Публикации с ключевыми словами: моделирование, прокатка, поперечно-винтовая прокатка
Публикации со словами: моделирование, прокатка, поперечно-винтовая прокатка
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||