научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2008
DOI: 10.7463/1108.0106658
УДК 519.6
МГТУ им. Н.Э. Баумана, 105005, Москва, 2-я Бауманская ул., д.5.
1. Введение
Современные обучающие системы представляют собой интеллектуальные системы, построенные на основе парадигмы обработки знаний. При этом формализация онтологии предметной области выполняется в виде базы знаний, которая может быть реализована на основе продукционная модели знаний, семантической сети, фреймовая модели знаний и на основе формальной логической модели знаний.
В работе полагается, что база знаний обучающей системы построена на основе семантической сети, содержащей понятия предметной области изучаемой дисциплины и отношения между этими понятиями. Семантическая сеть представляется в виде ориентированного графа, вершины которого соответствуют понятиям предметной области изучаемой дисциплины, а дуги задают отношение «определяемое понятие – определяющее понятие» между ними. Более строго, такая сеть классифицируется как однородная (с единственным типом отношений между понятиями) и бинарная (отношения связывают только по два понятия).
Полагается также, что обучающая система реализует способ создания учебных материалов на основе «сборки» их из предварительно разработанных модулей (module) или разделяемых единиц контента (SCO – ShareableContentObject). Такую технологию поддерживает широко известный стандарт SCORM[1], а также оригинальная отечественная разработка, называемая технологий разделяемых единиц контента (ТРЕК) [2]. В отличие от технологии SCORM, ТРЕК обеспечивает взаимосвязь между модулями путем задания указанных выше отношений между понятиями, определенными в этих модулях.
Важной задачей современной обучающей системы является педагогическая диагностика [3]. Стратегия диагностики, используемая в обучающей системе, зависит, прежде всего, от целей обучения, которые реализует эта система. Среди традиционных целей обучения выделяются следующие цели: приобретение знаний; приобретение навыки и приобретение умений [4]. Данная работа ориентирована на достижение первой из этих целей и связана с организацией контроля знаний в обучающей системе.
Контроль знаний в обучающей системе является многоплановой проблемой. В работе рассматривается одна из актуальных граней этой проблемы - контроль усвоения субъектом обучения понятий предметной области изучаемой дисциплины, а также взаимосвязей этих понятий [5].
Для решения задачи контроля понятийных знаний можно использовать тестовую подсистему обучающей системы или в рамках этой системы разрабатывать подсистему автоматического контроля понятийных знаний (см., например, программный продукт «Сеть научных понятий» [6]).
Во всех случаях для оценки уровня усвоения понятийных знаний, требуется оценка сложности понятий, модулей, репозитариев (библиотек) модулей и обучающих курсов. Эти же оценки необходимы для формирования индивидуальной образовательной траектории в интеллектуальной обучающей системе, менеджмента качества учебного процесса, проектирования учебных планов образовательных программ и пр.
Задачу оценки сложности учебного материала следует рассматривать в контексте более широкой задачи оценки качества этого материала. Данная задача не нова. Так еще в работе [7] предложена такая формальная мера сложности учебного материала, как мера его «разнообразия». Для вычисления значений этой меры используется классический подход Клода Шеннона: в качестве меры разнообразия принимается логарифм числа элементов, составляющих учебный материал.
В работе [8] с узлами семантической сети (понятиями) связывается картинка, видеоизображение, аудио-сегмент или текст и рассматриваются некоторые меры этих сущностей. В качестве одной из таких мер предлагается использовать меру количества информации по Колмогорову А.Н., заключенной в этой сущности. Значение указанной меры можно оценить размером соответствующего файла, сжатого с помощью современных алгоритмов сжатия.
В публикации [9] предлагается оценивать качество семантической сети с помощью следующих критериев: достоверность (степень безошибочности данных); кумулятивность (свойство данных небольшого объема достаточно полно отражать соответствующую предметную область); непротиворечивость (отсутствие взаимоисключающих понятий).
В диссертации [10] в качестве меры качества учебного материала предлагается использовать его объем, а также нечеткие экспертные оценки сложности этого материала.
В отличии от указанных работ, в данной работе меры сложности строятся на основе таких параметров семантической сети, как количество входных и выходных понятий, реберная плотность и диаметр графа, соответствующего этой сети и т.д.
Раздел 2 работы вводит основные обозначения. Некоторые меры сложности, рассматриваемые в работе, основаны на использование метрик графов. Поэтому в разделе 3 даны определения этих метрик. В разделе 4 рассматриваются меры сложности понятий, в разделах 5, 6 – меры сложности модулей, в разделах 7, 8 – меры сложности библиотек модулей, в разделах 9, 10 – меры сложности учебных курсов. В заключении сформулированы основные выводы.
Организация в обучающей системе контроля понятийных знаний субъекта обучения может требовать использования расширенной семантической сети [5], которую следует отнести к неоднородным и, возможно, N-арным семантическим сетям. К необходимости построения такой сети приводит также задача планирования в обучающей системе индивидуальной траектории обучения. В качестве меры сложности такой сети и ее фрагментов могут использоваться некоторые из мер, рассмотренных в данной работе. Систематическое рассмотрение мер сложности расширенной семантической сети, полагается, составит предмет самостоятельной публикации.
2. Модель семантической сети
2.1. Понятия и модули. Будем обозначать модули рассматриваемой библиотеки знаний ![]() ,
, ![]() Назовем входным понятием (inputconcept) модуля
Назовем входным понятием (inputconcept) модуля ![]() понятие
понятие ![]() , определение которого дано в некотором другом модуле библиотеки знаний
, определение которого дано в некотором другом модуле библиотеки знаний ![]() или иной библиотеке знаний. Набор входных понятий модуля
или иной библиотеке знаний. Набор входных понятий модуля ![]() обозначим
обозначим ![]() , где
, где ![]() - общее количество входных понятий. Из набора
- общее количество входных понятий. Из набора ![]() выделим входные понятия
выделим входные понятия ![]() , определенные в данной библиотеке знаний
, определенные в данной библиотеке знаний ![]() , и входные понятия
, и входные понятия ![]() , определение которых содержится в других библиотеках. Таким образом,
, определение которых содержится в других библиотеках. Таким образом, ![]() . Отметим, что одно или оба из множеств
. Отметим, что одно или оба из множеств ![]() ,
, ![]() могут быть пустыми.
могут быть пустыми.
Аналогично назовем выходным понятием (outputconcept) модуля ![]() понятие
понятие ![]() , определение которого дано в данном модуле
, определение которого дано в данном модуле ![]() . Набор выходных понятий модуля
. Набор выходных понятий модуля ![]() обозначим
обозначим ![]() , где
, где ![]() - общее количество выходных понятий.
- общее количество выходных понятий.
Каждое из понятий ![]() определяется через одно или несколько понятий из наборов
определяется через одно или несколько понятий из наборов ![]() ,
, ![]() . Обозначим
. Обозначим ![]() совокупность понятий набора
совокупность понятий набора ![]() , которые используются при определении понятия
, которые используются при определении понятия ![]() . Аналогично обозначим
. Аналогично обозначим ![]() понятия набора
понятия набора ![]() , которые используются при определении понятия
, которые используются при определении понятия ![]() . Здесь
. Здесь ![]() ,
, ![]() - количество таких понятий. Таким образом, будем полагать, что понятие
- количество таких понятий. Таким образом, будем полагать, что понятие ![]() определяется с помощью множества понятий
определяется с помощью множества понятий ![]() . Одно или оба из множеств
. Одно или оба из множеств ![]() ,
, ![]() могут быть пустыми. Отметим, что ситуация
могут быть пустыми. Отметим, что ситуация ![]() ,
, ![]() означает, что понятие
означает, что понятие ![]() определяется без привлечения других понятий.
определяется без привлечения других понятий.
Понятия из наборов ![]() ,
, ![]() будем называть информационно связанными (в узком смысле) с понятием
будем называть информационно связанными (в узком смысле) с понятием ![]() . Если понятие
. Если понятие ![]() информационно связано с понятием
информационно связано с понятием ![]() , и это понятие информационно связано с понятием
, и это понятие информационно связано с понятием ![]() , то будем говорить, что понятия
, то будем говорить, что понятия ![]() ,
, ![]() информационно связаны в широком смысле. Если понятие
информационно связаны в широком смысле. Если понятие ![]() , определенное в модуле
, определенное в модуле ![]() , информационно связано с понятием
, информационно связано с понятием ![]() , которое является входным понятием модуля
, которое является входным понятием модуля ![]() и, одновременно, выходным понятием модуля
и, одновременно, выходным понятием модуля ![]() , т.е.
, т.е. ![]() , то также будем говорить, что понятия
, то также будем говорить, что понятия ![]() ,
, ![]() информационно связаны в широком смысле.
информационно связаны в широком смысле.
Семантическую сеть ![]() модуля
модуля ![]() будем представлять в виде ориентированного графа без контуров
будем представлять в виде ориентированного графа без контуров ![]() , вершины которого соответствуют понятиям наборов
, вершины которого соответствуют понятиям наборов ![]() ,
, ![]() , а дуги отношениям «определяемое понятие – определяющее понятие» между ними. Другими словами, дуги в графе
, а дуги отношениям «определяемое понятие – определяющее понятие» между ними. Другими словами, дуги в графе ![]() соответствуют информационным связям понятий из наборов
соответствуют информационным связям понятий из наборов ![]() ,
, ![]() между собой.
между собой.
Введенные обозначения иллюстрирует Рис. 2.1. Модуль ![]() на этом рисунке использует три входных понятия
на этом рисунке использует три входных понятия ![]() ,
, ![]() ,
, ![]() (
(![]() ), и в модуле определены четыре выходных понятия
), и в модуле определены четыре выходных понятия ![]() ,
, ![]() ,
, ![]() ,
, ![]() (
(![]() ). Понятие
). Понятие ![]() , к примеру, определяется с помощью двух входных понятий модуля и двух его выходных понятий:
, к примеру, определяется с помощью двух входных понятий модуля и двух его выходных понятий: ![]() ;
; ![]() .
.

Рис. 2.1. Пример графа ![]() семантической сети модуля
семантической сети модуля ![]() .
.
Аналогично информационным связям понятий определены информационные связи моделей. Модули ![]() и
и ![]() будем называть информационно связанными модулями, если хотя бы одно выходное понятие модуля
будем называть информационно связанными модулями, если хотя бы одно выходное понятие модуля ![]() является входным понятием для модуля
является входным понятием для модуля ![]() или если хотя бы одно выходное понятие модуля
или если хотя бы одно выходное понятие модуля ![]() является входным понятием для модуля
является входным понятием для модуля ![]() .
.
Отметим следующее важное обстоятельство. В соответствие с концепцией технологии разделяемых единиц контента, одно и то же понятие может быть определено в разных модулях библиотеки знаний ![]() (в то же время, ни одно из понятий не может быть определено в разных модулях учебного курса
(в то же время, ни одно из понятий не может быть определено в разных модулях учебного курса ![]() ). Назовем такие понятия кратными понятиями. Кратность понятия
). Назовем такие понятия кратными понятиями. Кратность понятия ![]() обозначим
обозначим ![]() . Если не оговорено противное, будем далее полагать кратные понятия различными понятиями.
. Если не оговорено противное, будем далее полагать кратные понятия различными понятиями.
Современные интеллектуальные обучающие системы обеспечивают выполнение следующих правил расположения описаний понятий в модуле:
o ни одно из понятий k-го уровня ЯПФ модуля не может быть введено до тех пор, пока не определены все понятия всех расположенных ниже уровней ЯПФ (см. п. 3);
o при выполнении первого правила, описания понятий k-го уровня ЯПФ могут быть введены в модуле в произвольном порядке.
Наряду с этим современные обучающие системы разрешают использование в модуле понятий, которые еще не определены в данном модуле, а будет определены в нем позже. Такие понятия называются внутренними ссылочными понятиями. В терминах ЯПФ ссылка на понятие означает, что в тексте модуля при определении понятий k-го уровня используется понятие одного из расположенных выше уровней. Количество внутренних ссылочных понятий, используемых в модуле ![]() , обозначается
, обозначается ![]() .
.
Ссылочное понятие может быть также внешним ссылочным понятием. Если в тексте некоторого модуля ![]() учебного курса
учебного курса ![]() используется понятие, которое определено в модуле
используется понятие, которое определено в модуле ![]() ,
, ![]() , то для модуля
, то для модуля ![]() это понятие является внешним ссылочным. Здесь принято, что если
это понятие является внешним ссылочным. Здесь принято, что если ![]() , то модуль
, то модуль ![]() в курсе
в курсе ![]() текстуально расположен позже модуля
текстуально расположен позже модуля ![]() . Количество внешних ссылочных понятий модуля
. Количество внешних ссылочных понятий модуля ![]() обозначается
обозначается ![]() .
.
2.2. Библиотека модулей. Пусть библиотека модулей ![]() рассматриваемой предметной области состоит из M модулей
рассматриваемой предметной области состоит из M модулей ![]() , т.е.
, т.е. ![]() .
.
Семантическую сеть ![]() библиотеки
библиотеки ![]() будем представлять в виде ориентированных графов
будем представлять в виде ориентированных графов ![]() ,
, ![]() , первый из которых называется понятийным графом библиотеки
, первый из которых называется понятийным графом библиотеки ![]() , а второй – графом информационных связей модулей этой библиотеки или ее информационно-логическим графом. Графы,
, а второй – графом информационных связей модулей этой библиотеки или ее информационно-логическим графом. Графы, ![]() могут иметь контуры, количество которых обозначается
могут иметь контуры, количество которых обозначается ![]() ,
, ![]() , соответственно.
, соответственно.
Граф ![]() представляет собой объединение графов семантических сетей всех модулей библиотеки
представляет собой объединение графов семантических сетей всех модулей библиотеки ![]() , т.е.
, т.е. ![]() .
.
Вершины взвешенного мультиграфа ![]() соответствуют модулям библиотеки
соответствуют модулям библиотеки ![]() , а дуги – информационным связям модулям между собой. В отличие от графа
, а дуги – информационным связям модулям между собой. В отличие от графа ![]() , на рисунках дуги графа
, на рисунках дуги графа ![]() изображаются жирным; рядом с дугами в качестве их веса указываются количества информационных связей между соответствующими модулями. Другими словами, если
изображаются жирным; рядом с дугами в качестве их веса указываются количества информационных связей между соответствующими модулями. Другими словами, если ![]() выходных понятий модуля
выходных понятий модуля ![]() используются в качестве входных понятий модуля
используются в качестве входных понятий модуля ![]() , то рядом с соответствующей дугой в качестве ее веса указывается величина
, то рядом с соответствующей дугой в качестве ее веса указывается величина ![]() .
.
2.3. Учебный курс. Учебный курс, подготовленный из всех или некоторой совокупности модулей библиотеки ![]() , обозначается
, обозначается ![]() ;
; ![]() . В набор
. В набор ![]() входят модули
входят модули ![]() ,
, ![]() ,…,
,…,![]() библиотеки
библиотеки ![]() , где
, где ![]() - количество модулей в курсе
- количество модулей в курсе ![]() . Текстуально модули в учебном курсе
. Текстуально модули в учебном курсе ![]() расположены именно в порядке
расположены именно в порядке ![]() ,
, ![]() ,…,
,…,![]() , т.е. первым расположен модуль
, т.е. первым расположен модуль ![]() , вторым – модуль
, вторым – модуль ![]() и т.д.
и т.д.
Аналогично библиотеке ![]() , семантическую сеть
, семантическую сеть ![]() курса
курса ![]() будем представлять в виде ориентированных графов
будем представлять в виде ориентированных графов ![]() ,
, ![]() , где граф
, где граф ![]() называется понятийным графом курса
называется понятийным графом курса ![]() , а граф
, а граф ![]() – графом информационных связей модулей этого курса или, другими словами, его информационно-логическим графом. Поскольку допускаются контуры в графах
– графом информационных связей модулей этого курса или, другими словами, его информационно-логическим графом. Поскольку допускаются контуры в графах ![]() ,
, ![]() , графы
, графы ![]() ,
, ![]() также могут иметь контуры, количество которых обозначается
также могут иметь контуры, количество которых обозначается ![]() ,
, ![]() , соответственно.
, соответственно.
Граф ![]() представляет собой объединение графов семантических сетей всех модулей библиотеки
представляет собой объединение графов семантических сетей всех модулей библиотеки ![]() , входящих в учебный курс T, т.е.
, входящих в учебный курс T, т.е. ![]() .
.
Во взвешенном мультиграфе ![]() вершины соответствуют модулям
вершины соответствуют модулям ![]() ,
, ![]() ,…,
,…,![]() , а дуги – информационным связям модулям между собой. Аналогично графу
, а дуги – информационным связям модулям между собой. Аналогично графу ![]() , дуги графа
, дуги графа ![]() изображаются на рисунках жирным, а рядом с дугами в качестве их веса указывается кратность дуг.
изображаются на рисунках жирным, а рядом с дугами в качестве их веса указывается кратность дуг.
3. Метрики графа семантической сети
3.1. Высота графа. Рассмотрим ярусно-параллельную форму (ЯПФ) ориентированного графа без контуров ![]() [12]. ЯПФ орграфа
[12]. ЯПФ орграфа ![]() строится по следующему алгоритму:
строится по следующему алгоритму:
o на первый ярус ЯПФ помещаются все те вершины графа ![]() , в которые не входят дуги от других вершин графа;
, в которые не входят дуги от других вершин графа;
o ….
o на ![]() -й уровень помещаются те вершины графа
-й уровень помещаются те вершины графа ![]() , в которые входят дуги только от его вершин, расположенных на предыдущих
, в которые входят дуги только от его вершин, расположенных на предыдущих ![]() ярусах;
ярусах; ![]() .
.
Проиллюстрируем этот алгоритм на примере графа ![]() . Если множество
. Если множество ![]() не пусто, то на первом ярусе ЯПФ этого графа размещаются входные понятия
не пусто, то на первом ярусе ЯПФ этого графа размещаются входные понятия ![]() модуля
модуля ![]() ; на втором ярусе – понятия, определяемые только с помощью понятий
; на втором ярусе – понятия, определяемые только с помощью понятий ![]() ; на третьем ярусе – понятия, определяемые только с помощью понятий
; на третьем ярусе – понятия, определяемые только с помощью понятий ![]() и понятий второго яруса и т.д. (см. Рис. 3.1). Если модуль
и понятий второго яруса и т.д. (см. Рис. 3.1). Если модуль ![]() не использует входных понятий, т.е. если множество
не использует входных понятий, т.е. если множество ![]() пусто, то на первом ярусе соответствующей ЯПФ располагаются выходные понятия этого модуля, которые в своих определениях не содержат других понятий.
пусто, то на первом ярусе соответствующей ЯПФ располагаются выходные понятия этого модуля, которые в своих определениях не содержат других понятий.
Номер яруса ЯПФ графа ![]() , на котором находится вершина этого графа, называется высотой вершины, количество ярусов в ЯПФ графа
, на котором находится вершина этого графа, называется высотой вершины, количество ярусов в ЯПФ графа ![]() называется высотой ЯПФ этого графа (см. Рис. 3.1).
называется высотой ЯПФ этого графа (см. Рис. 3.1).

Рис. 3.1. Пример. Граф ![]() в ярусно-параллельной форме (см. Рис. 2.1).
в ярусно-параллельной форме (см. Рис. 2.1).
Высоту вершины ![]() в графе
в графе ![]() будем называть высотой понятия
будем называть высотой понятия ![]() и обозначать
и обозначать ![]() . Высота понятия зависит от контекста, в котором рассматривается данное понятие. Поясним данное утверждение примером.
. Высота понятия зависит от контекста, в котором рассматривается данное понятие. Поясним данное утверждение примером.
Пример 3.1. Пусть учебный курс T состоит из модулей ![]() ,
, ![]() , и граф
, и граф ![]() первого из них в ярусно-параллельной форме представлен на Рис. 3.1, а граф
первого из них в ярусно-параллельной форме представлен на Рис. 3.1, а граф ![]() второго, также в ярусно-параллельной форме, – на Рис. 3.2. Положим, что в качестве входных понятий модуля
второго, также в ярусно-параллельной форме, – на Рис. 3.2. Положим, что в качестве входных понятий модуля ![]() используются следующие понятия модуля
используются следующие понятия модуля ![]() :
: ![]() -
- ![]() ;
; ![]() -
- ![]() ;
; ![]() -
- ![]() . Тогда в ярусно-параллельной форме понятийный граф
. Тогда в ярусно-параллельной форме понятийный граф ![]() учебного курса T будет иметь вид, представленный на Рис. 3.3 (а). Из этого рисунка следует, что высота понятия
учебного курса T будет иметь вид, представленный на Рис. 3.3 (а). Из этого рисунка следует, что высота понятия ![]() в нем равна 6. Высота того же понятия в графе
в нем равна 6. Высота того же понятия в графе ![]() , представленном на Рис. 3.1, равна, легко видеть, 4
, представленном на Рис. 3.1, равна, легко видеть, 4![]()

Рис. 3.2. Пример. Граф ![]() модуля
модуля ![]() в ярусно-параллельной форме.
в ярусно-параллельной форме.

Рис. 3.3. К примеру 3.1. Графы ![]() ,
, ![]() учебного курса
учебного курса ![]() (см. Рис. 3.1, 3.2).
(см. Рис. 3.1, 3.2).
Контекст, в котором рассматривается высота понятия, будем обозначать надиндексом, так что ![]() ,
, ![]() ,
, ![]() - высоты понятия
- высоты понятия ![]() , определенного в модуле
, определенного в модуле ![]() , в библиотеке L и учебном курсе T, соответственно. В последнем случае полагается, что модуль
, в библиотеке L и учебном курсе T, соответственно. В последнем случае полагается, что модуль ![]() входит в число модулей курса T.
входит в число модулей курса T.
Высоту ЯПФ графа ![]() будем называть высотой модуля
будем называть высотой модуля ![]() и обозначать
и обозначать ![]() . По аналогии определяются высоты библиотеки
. По аналогии определяются высоты библиотеки ![]() ,
, ![]() и высоты учебного курса
и высоты учебного курса ![]() ,
, ![]() . Таким образом,
. Таким образом, ![]() ,
, ![]() - высоты библиотеки
- высоты библиотеки ![]() и курса
и курса ![]() для соответствующих понятийных графов, а
для соответствующих понятийных графов, а ![]() ,
, ![]() - те же высоты, но для графов информационных связей модулей.
- те же высоты, но для графов информационных связей модулей.
Легко видеть, например, что для курса T, состоящего из модулей ![]() ,
, ![]() (см. Рис. 3.3 (б)),
(см. Рис. 3.3 (б)), ![]() , а
, а ![]() .
.
В случае если граф ![]() имеет контуры, применение рассмотренного алгоритма построения его ЯПФ приводит к тому, что, начиная с некоторого уровня, оказывается невозможным ни одну из оставшихся вершин отнести к следующему уровню. При обнаружении этого факта необходимо разорвать одну или несколько из дуг, соединяющих оставшиеся вершины. Можно предложить несколько правил выбора таких дуг, например:
имеет контуры, применение рассмотренного алгоритма построения его ЯПФ приводит к тому, что, начиная с некоторого уровня, оказывается невозможным ни одну из оставшихся вершин отнести к следующему уровню. При обнаружении этого факта необходимо разорвать одну или несколько из дуг, соединяющих оставшиеся вершины. Можно предложить несколько правил выбора таких дуг, например:
o выбирается дуга, входящая в первую из оставшихся вершин;
o если в результате этой процедуры продолжение построения ЯПФ графа ![]() оказывается возможным, продолжить это построение;
оказывается возможным, продолжить это построение;
o в противном случае, по тому же правилу выбрать следующую дугу и т.д.
Разные правила выбора разрываемых дуг могут приводить к ЯПФ графа ![]() , имеющим разные высоты. С точки зрения мер сложности семантической сети, построенных на основе высоты ЯПФ соответствующих графов, вероятно, правильными были бы такие разрывы, которые приводят к максимальной высоте ЯПФ этих графов. Однако, с нашей точки зрения, решение такой задачи требует неоправданно больших вычислительных затрат и можно ограничиться рассмотренным выше правилом выбора разрезаемых дуг.
, имеющим разные высоты. С точки зрения мер сложности семантической сети, построенных на основе высоты ЯПФ соответствующих графов, вероятно, правильными были бы такие разрывы, которые приводят к максимальной высоте ЯПФ этих графов. Однако, с нашей точки зрения, решение такой задачи требует неоправданно больших вычислительных затрат и можно ограничиться рассмотренным выше правилом выбора разрезаемых дуг.
Будем далее полагать, что при построении ЯПФ графов ![]() ,
, ![]() ,
, ![]() ,
, ![]() , имеющих контуры, реализуется то или иное правило выбора разрываемых дуг, так что возможно построить ЯПФ этих графов и определить значения соответствующих высот.
, имеющих контуры, реализуется то или иное правило выбора разрываемых дуг, так что возможно построить ЯПФ этих графов и определить значения соответствующих высот.
Отметим, что при построении ЯПФ графа ![]() одновременно решается задача обнаружения факта наличия в нем контуров.
одновременно решается задача обнаружения факта наличия в нем контуров.
3.2. Диаметр графа. В качестве метрики графа ![]() нам понадобится также его диаметр
нам понадобится также его диаметр ![]() [13]. Диаметром графа (неориентированного)
[13]. Диаметром графа (неориентированного) ![]() называется максимальное расстояние между двумя вершинами этого графа. Расстоянием между вершинами графа называется минимальное количество ребер графа, связывающих эти вершины.
называется максимальное расстояние между двумя вершинами этого графа. Расстоянием между вершинами графа называется минимальное количество ребер графа, связывающих эти вершины.
Диаметр графа ![]() обозначается
обозначается ![]() . Кроме того, в работе используются диаметры
. Кроме того, в работе используются диаметры ![]() ,
, ![]() понятийных графов библиотеки
понятийных графов библиотеки ![]() и учебного курса T, а также диаметры
и учебного курса T, а также диаметры ![]() ,
, ![]() графов информационных связей модулей библиотеки Lи курса T, соответственно.
графов информационных связей модулей библиотеки Lи курса T, соответственно.
При вычислении диаметров графов, фигурирующих в работе, эти графы рассматриваются как неориентированные.
Рассмотрим для примера, граф ![]() , изображенный на Рис. 3.3(а). Расстояние между вершинами
, изображенный на Рис. 3.3(а). Расстояние между вершинами ![]() ,
, ![]() этого графа равно 2 (см. путь
этого графа равно 2 (см. путь ![]() ,
, ![]() ,
, ![]() , а не путь
, а не путь ![]() ,
, ![]() ,
, ![]() ,
, ![]() , например). Диаметр
, например). Диаметр ![]() того же графа равен 3, поскольку расстояние между двумя его самими удаленными вершинами
того же графа равен 3, поскольку расстояние между двумя его самими удаленными вершинами ![]() ,
, ![]() (или
(или ![]() ,
, ![]() ) равно 3. Диаметр
) равно 3. Диаметр ![]() графа
графа ![]() , приведенного на Рис. 3.3(б), равен 1.
, приведенного на Рис. 3.3(б), равен 1.
Отметим следующее обстоятельство. Поскольку при определении диаметра графа ![]() этот граф рассматривается как неориентированный граф, этот диаметр может быть найден и в том случае, когда граф
этот граф рассматривается как неориентированный граф, этот диаметр может быть найден и в том случае, когда граф ![]() имеет контуры.
имеет контуры.
3.3. Реберная плотность графа. Еще одной графовой метрикой, используемой в работе, является реберная плотность графа (ориентированного или неориентированного) ![]() [13], определяемая формулой
[13], определяемая формулой
![]() ,
,
где ![]() - количество дуг графа
- количество дуг графа ![]() , а
, а ![]() - количество его вершин. Реберная плотность
- количество его вершин. Реберная плотность ![]() и характеризует близость графа
и характеризует близость графа ![]() к полносвязному графу (клике): чем ближе
к полносвязному графу (клике): чем ближе ![]() к единице, тем выше связность графа
к единице, тем выше связность графа ![]() и он ближе к полносвязному графу.
и он ближе к полносвязному графу.
Реберную плотность графа ![]() будем обозначать
будем обозначать ![]() . Аналогично диаметрам
. Аналогично диаметрам ![]() ,
, ![]() ,
, ![]() ,
, ![]() , в работе используются реберные плотности
, в работе используются реберные плотности ![]() ,
, ![]() понятийных графов библиотеки
понятийных графов библиотеки ![]() и учебного курса T, а также реберные плотности
и учебного курса T, а также реберные плотности ![]() ,
, ![]() графов информационных связей модулей библиотеки Lи курса T, соответственно.
графов информационных связей модулей библиотеки Lи курса T, соответственно.
Рассмотрим для примера, графы ![]() ,
, ![]() изображенные на Рис. 3.3 (а), Рис. 3.3 (б). Реберные плотности этих графов равны, соответственно,
изображенные на Рис. 3.3 (а), Рис. 3.3 (б). Реберные плотности этих графов равны, соответственно, ![]() ,
, ![]() (поскольку граф
(поскольку граф ![]() является, очевидно, полносвязным графом).
является, очевидно, полносвязным графом).
Отметим следующее важное обстоятельство: реберная плотность графа имеет значительно меньшую вычислительную сложность, по сравнению вычислительной сложностью его высоты и диаметра.
4. Постановка задачи
Ставится следующая задача: сформировать меры сложности понятий ![]() , меры сложности модулей
, меры сложности модулей ![]() , меры сложности библиотек модулей
, меры сложности библиотек модулей ![]() и меры сложности учебных курсов
и меры сложности учебных курсов ![]() , значения которых можно определять автоматически - только путем анализа графов
, значения которых можно определять автоматически - только путем анализа графов ![]() ,
, ![]() и
и ![]() ,
, ![]() и
и ![]() , соответственно.
, соответственно.
Значение меры сложности понятия может зависеть от контекста, в котором производится оценка этой значения. В обозначениях меры сложности понятий соответствующий контекст будем указывать надиндексом. Так мера ![]() означает сложность понятия
означает сложность понятия ![]() в рамках модуля
в рамках модуля ![]() , мера
, мера ![]() - ту же сложность в рамках библиотеки
- ту же сложность в рамках библиотеки ![]() , мера
, мера ![]() - в пределах курса
- в пределах курса ![]() .
.
Аналогично мерам сложности понятий, вводятся меры сложности модулей ![]() ,
, ![]() ,
, ![]() .
.
Среди мер сложности библиотеки ![]() выделяются меры сложности, построенные на основе графов
выделяются меры сложности, построенные на основе графов ![]() ,
, ![]() . Будем обозначать эти меры
. Будем обозначать эти меры ![]() ,
, ![]() , соответственно.
, соответственно.
Аналогично вводятся меры сложности ![]() ,
, ![]() учебного курса
учебного курса ![]() .
.
Выделим два класса мер сложности понятий и модулей.
Меру сложности понятия ![]() будем называть контекстно-независимой мерой, если
будем называть контекстно-независимой мерой, если ![]() =
=![]() =
=![]() , и контекстно-зависимой мерой - в противном случае. Аналогично, мера сложности модуля
, и контекстно-зависимой мерой - в противном случае. Аналогично, мера сложности модуля ![]() называется контекстно-независимой, если
называется контекстно-независимой, если ![]() =
=![]() и
и ![]() =
=![]() , и контекстно-зависимой – иначе.
, и контекстно-зависимой – иначе.
Очевидно, что, при прочих равных условиях, определение значений контекстно-независимых мер требует меньших вычислительных затрат. Поэтому при отсутствии сильных преимуществ, мы будем стремиться к использованию именно этих мер.
Большие значения всех рассматриваемых в работе мер, соответствуют большим значениям сложности соответствующих объектов.
В работе предложено значительное количество мер сложности понятий, модулей, библиотек модулей и учебных курсов. В этой связи возникают следующие вопросы. Как много мер следует использовать? Какие из этих мер предпочтительнее? Каковы критерии такого выбора?
При поиске ответов на поставленные вопросы, на наш взгляд следует руководствоваться следующими соображениями.
1). Следует учитывать особенности человеческой системы переработки информации. Так результаты некоторых экспериментов показывают, что на пределе человеческих возможностей находится задача классификации объектов по трем классам, характеризуемых семью критериями и всего двумя градациями на шкалах их оценок [14]. Исходя из этого, можно рекомендовать использование, по возможности, не большего количества мер – не более семи.
2). Предпочтение следует отдавать тем мерам сложности, значения которых имеют простую содержательную интерпретацию.
3). При прочих равных условиях, преимуществом обладают меры, имеющие меньшую вычислительную сложность.
5. Меры сложности понятий
5.1. Мера сложности ![]() . Мера
. Мера ![]() представляет собой взвешенное количество понятий в наборах
представляет собой взвешенное количество понятий в наборах ![]() ,
, ![]() :
:
![]() , (5.1)
, (5.1)
где ![]() - весовой множитель.
- весовой множитель.
Как следует из формулы (5.1), мера ![]() , по сути, является двухкритериальной и представляет собой аддитивную свертку частных мер
, по сути, является двухкритериальной и представляет собой аддитивную свертку частных мер ![]() ,
, ![]() [15]. Содержательно мера
[15]. Содержательно мера ![]() означает, что выходное понятие модуля, при определении которого используется большее количество входных понятий этого модуля, а также других его выходных понятий, позиционируется как более сложное. Заметим, что в соответствии с определением меры
означает, что выходное понятие модуля, при определении которого используется большее количество входных понятий этого модуля, а также других его выходных понятий, позиционируется как более сложное. Заметим, что в соответствии с определением меры ![]() , мера входного понятия равна нулю:
, мера входного понятия равна нулю: ![]() .
.
Очевидно, что если вес ![]() один и тот же для всех модулей библиотеки
один и тот же для всех модулей библиотеки ![]() , то мера
, то мера ![]() не зависит от того контекста, в котором рассматривается понятие
не зависит от того контекста, в котором рассматривается понятие ![]() , т.е.
, т.е. ![]() . Таким образом, имеем
. Таким образом, имеем
Утверждение 5.1. Если во всех модулях библиотеки Lвес ![]() один и тот же, то мера
один и тот же, то мера ![]() является контекстно-независимой
является контекстно-независимой![]()
В качестве примера рассмотрим учебный курс T, граф семантической сети которого представлен на Рис. 3.3. Легко видеть, что справедливы следующие оценки: ![]() ,
, ![]() ,
, ![]() и т.д.
и т.д.
5.2. Мера сложности ![]() . В качестве меры сложности
. В качестве меры сложности ![]() рассматривается высота понятия
рассматривается высота понятия ![]() :
:
![]() . (5.2)
. (5.2)
Отметим, что в соответствии с этим определением сложность входных понятий модуля, а также понятий, при определении которых не используется ни одно из других понятий, равна единице.
Содержательно мера (5.2) означает следующее. Усвоение субъектом обучения понятия ![]() требует усвоения им также тех понятий уровня
требует усвоения им также тех понятий уровня ![]() , которые информационно связаны с понятием
, которые информационно связаны с понятием ![]() ; усвоение последних понятий требует усвоения соответствующих понятий уровня
; усвоение последних понятий требует усвоения соответствующих понятий уровня ![]() и т.д. до первого уровня. Таким образом, усвоение понятий, имеющих большую высоту, требует больших усилий. Поэтому логично полагать сложность понятия пропорциональной его высоте.
и т.д. до первого уровня. Таким образом, усвоение понятий, имеющих большую высоту, требует больших усилий. Поэтому логично полагать сложность понятия пропорциональной его высоте.
Поскольку высота понятия является контекстно-зависимой величиной (см. п. 3), имеет место
Утверждение 5.2. Мера ![]() является контекстно-зависимой и
является контекстно-зависимой и ![]() ,
, ![]()
![]()
Поясним последнее неравенство. Положим, что среди понятий, информационно-связанных с понятием ![]() , в библиотеке L содержится два кратных понятия, имеющих разную высоту. При формировании учебного курса T в него войдет только одно из этих понятий. Если этим понятием будет понятие с меньшей высотой, то имеем
, в библиотеке L содержится два кратных понятия, имеющих разную высоту. При формировании учебного курса T в него войдет только одно из этих понятий. Если этим понятием будет понятие с меньшей высотой, то имеем ![]() , в противном случае -
, в противном случае - ![]() .
.
Рассмотрим в качестве примера модуль ![]() (см. Рис. 3.2). Для этого модуля имеем:
(см. Рис. 3.2). Для этого модуля имеем: ![]() ,
, ![]() и т.д. Для курса T, граф семантической сети которого представлен на Рис. 3.3, аналогично имеем
и т.д. Для курса T, граф семантической сети которого представлен на Рис. 3.3, аналогично имеем ![]() ,
, ![]() и т.д.
и т.д.
5.3. Мера ![]() . В качестве меры
. В качестве меры ![]() используется количество понятий, информационно связанных в широком смысле с понятием
используется количество понятий, информационно связанных в широком смысле с понятием ![]() .
.
Очевидно, что если высота понятия ![]() равна единице, то мера
равна единице, то мера ![]() совпадает с мерой
совпадает с мерой ![]() и ее значение равно нулю.
и ее значение равно нулю.
Для определения значений мер ![]() ,
, ![]() следует в библиотеке Lи учебном курсе Tподсчитать общие количества понятий, информационно связанных в широком смысле с понятием
следует в библиотеке Lи учебном курсе Tподсчитать общие количества понятий, информационно связанных в широком смысле с понятием ![]() , соответственно.
, соответственно.
Аналогично утверждению 5.2 имеем
Утверждение 5.3. Мера ![]() является контекстно-зависимой и
является контекстно-зависимой и ![]() ,
, ![]()
![]()
Для примера, рассмотрим модуль ![]() (см. Рис. 3.1) и учебный курс T(см. Рис. 3.3). Из указанных рисунков легко видеть, что имеют место следующие оценки:
(см. Рис. 3.1) и учебный курс T(см. Рис. 3.3). Из указанных рисунков легко видеть, что имеют место следующие оценки: ![]() ,
, ![]() ;
; ![]() ,
, ![]() .
.
5.4. Мультимера ![]() представляет собой аддитивную свертку мер
представляет собой аддитивную свертку мер ![]() ,
, ![]() ,
, ![]() :
:
![]() , (5.3)
, (5.3)
где ![]() - вектор весовых множителей;
- вектор весовых множителей; ![]() ,
, ![]() .
.
Аддитивная свертка частных критериев оптимальности, используемая (5.3), является наиболее популярным приемом сведения многокритериальной задачи к однокритериальной. Наряду с этим могут использоваться мультипликативные свертки, лексикографическое упорядочение и пр. [15]. Мы здесь и далее ограничимся только аддитивной сверткой.
Из утверждений 5.1 – 5.3 вытекает справедливость следующего утверждения.
Утверждение 5.4. Мультимера ![]() является контекстно-зависимой и
является контекстно-зависимой и ![]() ,
, ![]()
![]()
Положим ![]() ,
, ![]() и рассмотрим в качестве примера сложность понятия
и рассмотрим в качестве примера сложность понятия ![]() (см. Рис. 3.2). Легко видеть, что
(см. Рис. 3.2). Легко видеть, что ![]() ,
, ![]() ,
, ![]() . Таким образом,
. Таким образом,
![]() .
.
Резюмируя данный раздел, отметим, что с точки зрения простоты интерпретации и минимума вычислительной сложности, из числа рассмотренных мер сложности понятий к применению можно рекомендовать меру ![]() - взвешенное количество понятий, через которое определяется данное понятие, а также меру
- взвешенное количество понятий, через которое определяется данное понятие, а также меру ![]() - количество понятий, информационно связанных в широком смысле с данным понятием. Другими словами, можно рекомендовать к использоваиню мультимеру
- количество понятий, информационно связанных в широком смысле с данным понятием. Другими словами, можно рекомендовать к использоваиню мультимеру ![]() , в которой
, в которой ![]() ,
, ![]() .
.
6. Меры сложности модулей, построенные на основе мер сложности понятий
. 6.1. Меры сложности ![]() ,
, ![]() строятся на основе меры сложности понятий
строятся на основе меры сложности понятий ![]() (см. п. 5.1):
(см. п. 5.1):
![]() ,
, ![]() ; (6.1)
; (6.1)
![]() . (6.2)
. (6.2)
Т.е. мера ![]() представляет собой сумму мер
представляет собой сумму мер ![]() всех выходных понятий модуля
всех выходных понятий модуля ![]() , а мера
, а мера ![]() - ту же меру
- ту же меру ![]() , но усредненную по количеству этих понятий. Другими словами, меры
, но усредненную по количеству этих понятий. Другими словами, меры ![]() ,
, ![]() - это сумма и усредненная сумма количеств понятий, связанных в узком смысле с каждым из выходных понятий модуля
- это сумма и усредненная сумма количеств понятий, связанных в узком смысле с каждым из выходных понятий модуля ![]() , соответственно. Отметим, что входные понятия модуля
, соответственно. Отметим, что входные понятия модуля ![]() не учитываются в формулах (6.1), (6.2) потому, что их мера
не учитываются в формулах (6.1), (6.2) потому, что их мера ![]() равна нулю (см. п. 5.1).
равна нулю (см. п. 5.1).
Поскольку мера ![]() не зависит от контекста (см. Утверждение 5.1), меры
не зависит от контекста (см. Утверждение 5.1), меры ![]() ,
, ![]() также не зависят от контекста, т.е.
также не зависят от контекста, т.е. ![]() ,
, ![]() . Таким образом, имеем
. Таким образом, имеем
Утверждение 6.1. Меры ![]() ,
, ![]() является контекстно-независимыми
является контекстно-независимыми![]()
Рассмотрим для примера модуль ![]() (см. Рис. 3.2). Легко видеть, что
(см. Рис. 3.2). Легко видеть, что ![]() ,
, ![]() ;
; ![]()
![]() ;
; ![]() .
.
6.2. Меры сложности ![]() ,
, ![]() . Меры
. Меры ![]() ,
, ![]() формируются на основе меры
формируются на основе меры ![]() (см. п. 5.2):
(см. п. 5.2):
![]() ,
, ![]() ,
, ![]() ; (6.3)
; (6.3)
 . (6.4)
. (6.4)
Таким образом, аналогично мерам ![]() ,
, ![]() , мера
, мера ![]() представляет собой сумму мер
представляет собой сумму мер ![]() всех входных и выходных понятий модуля
всех входных и выходных понятий модуля ![]() , а мера
, а мера ![]() - ту же меру
- ту же меру ![]() , но усредненную по суммарному количеству входных и выходных понятий модуля
, но усредненную по суммарному количеству входных и выходных понятий модуля ![]() . Другими словами, меры
. Другими словами, меры ![]() ,
, ![]() есть сумма и усредненная сумма высот всех входных и выходных понятий модуля
есть сумма и усредненная сумма высот всех входных и выходных понятий модуля ![]() , соответственно. В отличие от мер
, соответственно. В отличие от мер ![]() ,
, ![]() , входные понятия модуля
, входные понятия модуля ![]() учитываются в формулах (6.3), (6.4), поскольку для этих понятий мера
учитываются в формулах (6.3), (6.4), поскольку для этих понятий мера ![]() не равна нулю (см. п. 5.2).
не равна нулю (см. п. 5.2).
Из того факта, что мера ![]() является контекстно-зависимой (см. Утверждение 5.2), следует справедливость следующего утверждения.
является контекстно-зависимой (см. Утверждение 5.2), следует справедливость следующего утверждения.
Утверждение 6.2. Меры ![]() ,
, ![]() являются контекстно-зависимыми и
являются контекстно-зависимыми и
![]() ,
, ![]() ;
; ![]() ,
, ![]()
![]()
В качестве примера рассмотрим модуль ![]() , граф семантической сети которого приведен на Рис. 3.1. Из этого рисунка следует, что:
, граф семантической сети которого приведен на Рис. 3.1. Из этого рисунка следует, что: ![]() =
=![]() =
=![]() =1;
=1; ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Таким образом,
. Таким образом,
![]() ,
,
![]() .
.
6.3. Меры сложности ![]() ,
, ![]() . Меры
. Меры ![]() ,
, ![]() формируются на основе меры
формируются на основе меры ![]() (см. п. 5.3):
(см. п. 5.3):
![]() ,
, ![]() ; (6.5)
; (6.5)
![]() . (6.6)
. (6.6)
Таким образом, меры ![]() ,
, ![]() представляют собой сумму и усредненную сумму количеств выходных понятий, информационно связанных в широком смысле с каждым из понятий модуля
представляют собой сумму и усредненную сумму количеств выходных понятий, информационно связанных в широком смысле с каждым из понятий модуля ![]() , соответственно. Поскольку мера
, соответственно. Поскольку мера ![]() входных понятий модуля равна нулю (см. п. 5.3), в отличие от мер
входных понятий модуля равна нулю (см. п. 5.3), в отличие от мер ![]() ,
, ![]() , меры (6.5), (6.6) не включают в себя меры сложность этих понятий.
, меры (6.5), (6.6) не включают в себя меры сложность этих понятий.
Из утверждения 5.3 вытекает справедливость следующего утверждения.
Утверждение 6.3. Меры ![]() ,
, ![]() являются контекстно-зависимыми и
являются контекстно-зависимыми и
![]() ,
, ![]() ;
; ![]() ,
, ![]()
![]()
Рассмотрим для примера модуль ![]() (см. Рис. 3.2). Из того факта, что
(см. Рис. 3.2). Из того факта, что ![]() ,
, ![]() , имеем:
, имеем:
![]() ;
;
![]() .
.
6.4. Мультимеры сложности ![]() ,
, ![]() формируются на основе мультимеры
формируются на основе мультимеры ![]() (см. п. 5.4) и определяются выражениями
(см. п. 5.4) и определяются выражениями
![]() ,
, ![]() ,
, ![]() , (6.7)
, (6.7)
 . (6.8)
. (6.8)
Таким образом, меры ![]() ,
, ![]() представляют собой сумму и усредненную сумму значений аддитивной свертки мер
представляют собой сумму и усредненную сумму значений аддитивной свертки мер ![]() ,
, ![]() ,
, ![]() для всех понятий (и входных и выходных) модуля
для всех понятий (и входных и выходных) модуля ![]() , соответственно.
, соответственно.
Из утверждения 5.4 вытекает справедливость следующего утверждения.
Утверждение 6.4. Меры ![]() ,
, ![]() являются контекстно-зависимыми и
являются контекстно-зависимыми и ![]() ,
, ![]()
![]()
Положим ![]() ,
, ![]() и рассмотрим для примера модуль
и рассмотрим для примера модуль ![]() (см. Рис. 3.2). Для понятий
(см. Рис. 3.2). Для понятий ![]() ,
, ![]() ,
, ![]() ,
, ![]() имеем, соответственно:
имеем, соответственно:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Таким образом,
![]()
![]()
![]()
![]()
![]()
и
![]() .
.
Замечание. На основе мер ![]() ,
, ![]() ,
, ![]() можно сконструировать меры, отличные от рассмотренных в пп. 6.1 – 6.3 и основанные на использовании принципа гарантированного результата [16]. Например, на основе меры
можно сконструировать меры, отличные от рассмотренных в пп. 6.1 – 6.3 и основанные на использовании принципа гарантированного результата [16]. Например, на основе меры ![]() можно построить меру
можно построить меру
![]() ,
, ![]() . (6.9)
. (6.9)
Эта мера имеет смысл максимальной высоты выходных понятий в модуле ![]() , т.е. представляет собой высоту ЯПФ этого модуля. Содержательно мера
, т.е. представляет собой высоту ЯПФ этого модуля. Содержательно мера ![]() означает, что более сложным тот модуль, который содержит понятие большей высоты.
означает, что более сложным тот модуль, который содержит понятие большей высоты.
С нашей точки зрения мера (6.9) менее содержательна, чем меры (6.3), (6.4), поскольку может приводить к одинаковым оценкам сложности двух модулей, первый из которых содержит только одно выходное понятие высоты ![]() , а второй - множество выходных понятий, максимальная высота которых также равна
, а второй - множество выходных понятий, максимальная высота которых также равна ![]() . Интуитивно равная оценка сложности таких модулей представляется неверной. Поэтому оценка (6.9) и аналогичные ей оценки далее не рассматриваются
. Интуитивно равная оценка сложности таких модулей представляется неверной. Поэтому оценка (6.9) и аналогичные ей оценки далее не рассматриваются![]()
7. Прочие меры сложности модулей
7.1. Мера сложности ![]() представляет собой взвешенную сумму количеств входных и выходных понятий модуля
представляет собой взвешенную сумму количеств входных и выходных понятий модуля ![]() , т.е. взвешенное суммарное количество понятий в наборах
, т.е. взвешенное суммарное количество понятий в наборах ![]() ,
, ![]() :
:
![]() . (7.1)
. (7.1)
Здесь ![]() - множитель, определяющий относительный вес входных и выходных понятий.
- множитель, определяющий относительный вес входных и выходных понятий.
Аналогично мере ![]() (см. п. 5.1), мера
(см. п. 5.1), мера ![]() является двухкритериальной и представляет собой аддитивную свертку величин
является двухкритериальной и представляет собой аддитивную свертку величин ![]() ,
, ![]() . Содержательно мера (7.1) означает, что модуль, который оперирует большим количеством понятий, является, с нашей точки зрения, более сложным.
. Содержательно мера (7.1) означает, что модуль, который оперирует большим количеством понятий, является, с нашей точки зрения, более сложным.
Очевидно, что при любом ![]() мера
мера ![]() не зависит от контекста:
не зависит от контекста: ![]() . Таким образом, имеем
. Таким образом, имеем
Утверждение 7.1. Мера ![]() является контекстно-независимой
является контекстно-независимой![]()
В качестве примера рассмотрим модуль ![]() , граф семантической сети которого представлен на Рис. 3.1. Легко видеть, что для этого модуля
, граф семантической сети которого представлен на Рис. 3.1. Легко видеть, что для этого модуля ![]() , а
, а ![]() .
.
7.2. Мера сложности ![]() является взвешенной суммой количеств внешних и внутренних ссылочных понятий, используемых в модуле
является взвешенной суммой количеств внешних и внутренних ссылочных понятий, используемых в модуле ![]() :
:
![]() . (7.2)
. (7.2)
Здесь аналогично мере ![]() , весовой множитель
, весовой множитель ![]() , а мера
, а мера ![]() представляет собой аддитивную свертку величин
представляет собой аддитивную свертку величин ![]() ,
, ![]() .
.
Содержательно мера (7.2) означает, что более сложным полагается модуль, в котором используется большее количество внутренних и внешних ссылочных понятий. Очевидно, что при любом ![]() мера
мера ![]() не зависит от контекста (т.е.
не зависит от контекста (т.е. ![]() ) и справедливо
) и справедливо
Утверждение 7.2. Мера ![]() является контекстно-независимой
является контекстно-независимой![]()
7.3. Мера сложности ![]() - диаметр графа
- диаметр графа ![]() , соответствующего семантической сети модуля
, соответствующего семантической сети модуля ![]() :
:
![]() . (7.3)
. (7.3)
Содержательно мера ![]() характеризует размер графа
характеризует размер графа ![]() и предполагает большую сложность модуля в случае, если этот размер больше. Очевидно, что мера
и предполагает большую сложность модуля в случае, если этот размер больше. Очевидно, что мера ![]() не зависит от контекста, т.е.
не зависит от контекста, т.е. ![]() и справедливо
и справедливо
Утверждение 7.3. Мера ![]() является контекстно-независимой
является контекстно-независимой![]()
В качестве примера так же, как в п. 7.1, рассмотрим модуль ![]() (см. Рис. 3.1). Легко видеть, что в этом случае
(см. Рис. 3.1). Легко видеть, что в этом случае ![]() .
.
7.4. Мера сложности ![]() представляет собой реберную плотность графа
представляет собой реберную плотность графа ![]() , соответствующего семантической сети модуля
, соответствующего семантической сети модуля ![]() :
:
![]() . (7.4)
. (7.4)
Содержательно мера ![]() характеризует близость графа
характеризует близость графа ![]() к клике и предполагает большую сложность модуля
к клике и предполагает большую сложность модуля ![]() в случае, когда этот граф ближе к полносвязному графу. Как и мера
в случае, когда этот граф ближе к полносвязному графу. Как и мера ![]() , мера
, мера ![]() , очевидно, не зависит от контекста, т.е.
, очевидно, не зависит от контекста, т.е. ![]() и справедливо
и справедливо
Утверждение 7.4. Мера ![]() является контекстно-независимой
является контекстно-независимой![]()
В качестве примера опять же рассмотрим модуль ![]() (см. Рис. 3.1). В этом случае
(см. Рис. 3.1). В этом случае ![]() .
.
7.5. Мультимера ![]() - аддитивная свертка мер
- аддитивная свертка мер ![]() -
- ![]() :
:
![]() . (7.5)
. (7.5)
Здесь для простоты записи опущены весовые множители в выражениях для ![]() ,
, ![]() ,
, ![]() , а вектор весовых множителей
, а вектор весовых множителей ![]() ;
; ![]() ,
, ![]() .
.
Из утверждений 6.1 – 6.3, 7.1 – 7.4 следует справедливость следующего утверждения.
Утверждение 7.5. Мультимера ![]() является контекстно-зависимой и
является контекстно-зависимой и ![]() ,
, ![]()
![]()
Замечание 7.1. Каждая из рассмотренных мер сложности модулей может служить также мерой такого показателя дидактического качества учебного материала, как его усвояемость [17]. Действительно, большое значение всех мер сложности, рассмотренных в п. 6, а также мер ![]() ,
, ![]() ,
, ![]() , рассмотренные в данном разделе, может означать, что конструктор курса слишком много материала включил в эти модули. Большие же размеры модулей затрудняют усвоение соответствующего учебного материала. Отметим, что в соответствие с концепцией ТРЕК, размер каждого из модулей библиотеки базы знаний должен быть невелик.
, рассмотренные в данном разделе, может означать, что конструктор курса слишком много материала включил в эти модули. Большие же размеры модулей затрудняют усвоение соответствующего учебного материала. Отметим, что в соответствие с концепцией ТРЕК, размер каждого из модулей библиотеки базы знаний должен быть невелик.
Отдельного обсуждения с этой точки зрения заслуживает мера сложности ![]() . Конечно же, наличие в модулях внутренних и внешних ссылок, делает их более сложными. Однако, поскольку эти ссылки значительно затрудняют восприятие учебного материала субъектом обучения, наличие их значительного количества в большей степени свидетельствует о низкой усвояемости этого материала
. Конечно же, наличие в модулях внутренних и внешних ссылок, делает их более сложными. Однако, поскольку эти ссылки значительно затрудняют восприятие учебного материала субъектом обучения, наличие их значительного количества в большей степени свидетельствует о низкой усвояемости этого материала![]()
Резюмируя разделы 6, 7, приведем наши рекомендации по применению рассмотренных мер сложности модулей. Из соображений простоты интерпретации и минимума вычислительной сложности мы рекомендуем использовать меру ![]() - взвешенную сумму количеств входных и выходных понятий данного модуля, меру
- взвешенную сумму количеств входных и выходных понятий данного модуля, меру ![]() - взвешенное количество внешних и внутренних ссылочных понятий, используемых в данном модуле, а также меру
- взвешенное количество внешних и внутренних ссылочных понятий, используемых в данном модуле, а также меру ![]() - реберную плотность графа, соответствующего семантической сети данного модуля. Более строго говоря, мы рекомендуем использовать мультимеру
- реберную плотность графа, соответствующего семантической сети данного модуля. Более строго говоря, мы рекомендуем использовать мультимеру ![]() при
при ![]() ,
, ![]() .
.
8. Меры сложности библиотек модулей, построенных на основе меры сложности модулей
. 8.1. Меры сложности ![]() ,
, ![]() строятся на основе мер сложности модулей
строятся на основе мер сложности модулей ![]() ,
, ![]() , соответственно, (см. п. 6.1). Поскольку эти меры являются контекстно-независимыми (см. Утверждение 6.1), в качестве мер
, соответственно, (см. п. 6.1). Поскольку эти меры являются контекстно-независимыми (см. Утверждение 6.1), в качестве мер ![]() ,
, ![]() можно использовать суммы
можно использовать суммы
![]() ,
, ![]() . (8.1)
. (8.1)
Таким образом, мера ![]() представляет собой сумму количеств понятий, связанных в узком смысле с каждым из выходных понятий каждого из модулей библиотеки L, а мера
представляет собой сумму количеств понятий, связанных в узком смысле с каждым из выходных понятий каждого из модулей библиотеки L, а мера ![]() - сумму усредненных в пределах каждого из модулей количеств тех же понятий.
- сумму усредненных в пределах каждого из модулей количеств тех же понятий.
Здесь и далее в этом разделе в качестве примера мы будем использовать библиотеку ![]() , состоящую из модулей
, состоящую из модулей ![]() ,
, ![]() (см. Рис. 3.1, 3.2).
(см. Рис. 3.1, 3.2).
Таким образом, последовательно имеем:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() ,
, ![]() (см. п. (6.1));
(см. п. (6.1));
![]() ;
;
![]() .
.
На основе мер сложности модулей ![]() ,
, ![]() можно предложить и другие меры сложности библиотеки L. Например, естественно использовать усреднение мер (8.1) по количеству модулей
можно предложить и другие меры сложности библиотеки L. Например, естественно использовать усреднение мер (8.1) по количеству модулей ![]() :
:
![]() ; (8.2)
; (8.2)
![]() . (8.3)
. (8.3)
8.2. Меры сложности ![]() ,
, ![]() формируются на основе мер сложности модулей
формируются на основе мер сложности модулей ![]() ,
, ![]() , соответственно (см. п. 6.2). Поскольку меры
, соответственно (см. п. 6.2). Поскольку меры ![]() ,
, ![]() являются контекстно-зависимыми (см. Утверждение 6.2), возможны два метода формирования мер
являются контекстно-зависимыми (см. Утверждение 6.2), возможны два метода формирования мер ![]() ,
, ![]() .
.
1). Построение мер ![]() ,
, ![]() на основе непосредственно мер
на основе непосредственно мер ![]() ,
, ![]() , т.е. с использованием значений этих мер в контексте соответствующих модулей:
, т.е. с использованием значений этих мер в контексте соответствующих модулей:
![]() ;
; ![]() . (8.4)
. (8.4)
2). Построение мер ![]() ,
, ![]() на основе мер
на основе мер ![]() ,
, ![]() в контексте всей библиотеки, т.е. на основе мер
в контексте всей библиотеки, т.е. на основе мер ![]() ,
, ![]() :
:
![]() ;
; ![]() (8.5)
(8.5)
На основе мер ![]() ,
, ![]() ,
, ![]() ,
, ![]() можно также предложить меры, аналогичные мерам (8.2), (8.3).
можно также предложить меры, аналогичные мерам (8.2), (8.3).
Мера ![]() представляет собой сумму высот входных и выходных понятий всех модулей библиотеки Lв случае, когда каждая из этих высот определяется в контексте соответствующего модуля. Аналогично, мера
представляет собой сумму высот входных и выходных понятий всех модулей библиотеки Lв случае, когда каждая из этих высот определяется в контексте соответствующего модуля. Аналогично, мера ![]() есть сумма высот тех же понятий, усредненных в пределах каждого из модулей библиотеки L. Мера
есть сумма высот тех же понятий, усредненных в пределах каждого из модулей библиотеки L. Мера ![]() есть ни что иное, как сумма высот входных и выходных понятий всех модулей библиотеки Lв случае, когда каждая из этих высот определяется в контексте библиотеки L. Аналогично, мера
есть ни что иное, как сумма высот входных и выходных понятий всех модулей библиотеки Lв случае, когда каждая из этих высот определяется в контексте библиотеки L. Аналогично, мера ![]() представляет собой сумму высот этих понятий, усредненных в пределах каждого из модулей библиотеки L.
представляет собой сумму высот этих понятий, усредненных в пределах каждого из модулей библиотеки L.
К примеру, для библиотеки ![]() имеем следующие значения рассматриваемых мер.
имеем следующие значения рассматриваемых мер.
1). Меры ![]() ,
, ![]() (см. Рис. 3.1, 3.2):
(см. Рис. 3.1, 3.2):
![]() ,
, ![]() (см. п. (6.1));
(см. п. (6.1));
![]() ,
, ![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() ,
, ![]() .
.
2). Меры ![]() ,
, ![]() (см. Рис. 3.3 (а)):
(см. Рис. 3.3 (а)):
![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() ;
; ![]() .
.
8.3. Меры сложности ![]() ,
, ![]() основаны на мерах сложности
основаны на мерах сложности ![]() ,
, ![]() (см. п. 6.3). Поскольку меры
(см. п. 6.3). Поскольку меры ![]() ,
, ![]() являются контекстно-зависимыми (см. Утверждение 6.3), аналогично п. 8.2 возможны два метода формирования мер
являются контекстно-зависимыми (см. Утверждение 6.3), аналогично п. 8.2 возможны два метода формирования мер ![]() ,
, ![]() :
:
![]() ,
, ![]() ; (8.6)
; (8.6)
![]() ,
, ![]() . (8.7)
. (8.7)
На основе мер ![]() ,
, ![]() ,
, ![]() ,
, ![]() можно также предложить меры, аналогичные мерам (8.2), (8.3).
можно также предложить меры, аналогичные мерам (8.2), (8.3).
Мера ![]() есть сумма количеств понятий, информационно связанных в широком смысле с каждым из понятий всех модулей библиотеки Lв случае, когда каждая из этих сумм определяется в контексте соответствующего модуля. Аналогично, мера
есть сумма количеств понятий, информационно связанных в широком смысле с каждым из понятий всех модулей библиотеки Lв случае, когда каждая из этих сумм определяется в контексте соответствующего модуля. Аналогично, мера ![]() - это сумма количеств тех же понятий, усредненных в пределах каждого из модулей библиотеки L. Мера
- это сумма количеств тех же понятий, усредненных в пределах каждого из модулей библиотеки L. Мера ![]() представляет собой сумму количеств понятий, информационно связанных в широком смысле с каждым из понятий всех модулей библиотеки Lв случае, когда каждая из этих сумм определяется в контексте библиотеки L. Аналогично, мера
представляет собой сумму количеств понятий, информационно связанных в широком смысле с каждым из понятий всех модулей библиотеки Lв случае, когда каждая из этих сумм определяется в контексте библиотеки L. Аналогично, мера ![]() является суммой количеств этих понятий, усредненных в пределах каждого из модулей библиотеки L.
является суммой количеств этих понятий, усредненных в пределах каждого из модулей библиотеки L.
Для библиотеки ![]() имеем следующие значения рассматриваемых мер.
имеем следующие значения рассматриваемых мер.
1). Меры ![]() ,
, ![]() (см. Рис. 3.1, 3.2):
(см. Рис. 3.1, 3.2):
![]() ,
, ![]() ,
, ![]() ,
, ![]() :
:
![]() ,
, ![]() ;
;
![]() ,
, ![]() (см. п. 6.3);
(см. п. 6.3);
![]() ,
, ![]() .
.
2). Меры ![]() ,
, ![]() (см. Рис. 3.3(а)):
(см. Рис. 3.3(а)):
![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() ,
, ![]() (см. п. 6.3);
(см. п. 6.3);
![]() ;
; ![]() .
.
8.4. Меры сложности ![]() ,
, ![]() формируются на основе контекстно-зависимых мультимер
формируются на основе контекстно-зависимых мультимер ![]() ,
, ![]() (см. п. 6.4) и аналогично пп. 8.2, 8.3 равны
(см. п. 6.4) и аналогично пп. 8.2, 8.3 равны
![]() ,
, ![]() , (8.8)
, (8.8)
![]() ,
, ![]() . (8.9)
. (8.9)
На основе мер ![]() ,
, ![]() ;
; ![]() ,
, ![]() можно также предложить меры, аналогичные мерам (8.2), (8.3).
можно также предложить меры, аналогичные мерам (8.2), (8.3).
Таким образом, мера ![]() есть сумма значений аддитивной свертки мер
есть сумма значений аддитивной свертки мер ![]() ,
, ![]() ,
, ![]() для всех понятий всех модулей библиотеки Lв случае, когда каждая из этих сверток определяется в контексте соответствующего модуля. Аналогично, мера
для всех понятий всех модулей библиотеки Lв случае, когда каждая из этих сверток определяется в контексте соответствующего модуля. Аналогично, мера ![]() - это сумма значений аддитивной свертки тех же мер, усредненных в пределах каждого из модулей библиотеки L. Мера
- это сумма значений аддитивной свертки тех же мер, усредненных в пределах каждого из модулей библиотеки L. Мера ![]() представляет собой сумма значений аддитивной свертки мер
представляет собой сумма значений аддитивной свертки мер ![]() ,
, ![]() ,
, ![]() для всех понятий всех модулей библиотеки Lв случае, когда каждая из этих сверток определяется в контексте библиотеки L. Аналогично, мера
для всех понятий всех модулей библиотеки Lв случае, когда каждая из этих сверток определяется в контексте библиотеки L. Аналогично, мера ![]() является суммой значений аддитивной свертки тех же мер, усредненных в пределах каждого из модулей библиотеки L.
является суммой значений аддитивной свертки тех же мер, усредненных в пределах каждого из модулей библиотеки L.
8.5. Меры сложности ![]() ,
, ![]() строятся на основе контекстно-независимой меры
строятся на основе контекстно-независимой меры ![]() (см. Утверждение 7.1) и поэтому аналогично мерам
(см. Утверждение 7.1) и поэтому аналогично мерам ![]() ,
, ![]() равны
равны
![]() ,
, ![]() , (8.10)
, (8.10)
где ![]() .
.
Таким образом, мера ![]() представляет собой сумму взвешенных сумм количеств входных и выходных понятий всех модулей библиотеки L, а мера
представляет собой сумму взвешенных сумм количеств входных и выходных понятий всех модулей библиотеки L, а мера ![]() - ту же сумму, усредненную по количеству модулей M в библиотеке L.
- ту же сумму, усредненную по количеству модулей M в библиотеке L.
Используя в качестве примера библиотеку ![]() , при
, при ![]() получим следующие значения мер
получим следующие значения мер ![]() ,
, ![]() :
:
![]() ,
, ![]() ;
;
![]() ,
, ![]() .
.
8.6. Меры сложности ![]() ,
, ![]() строятся на основе контекстно-независимой меры
строятся на основе контекстно-независимой меры ![]() (см. Утверждение 7.2) и поэтому аналогично мерам
(см. Утверждение 7.2) и поэтому аналогично мерам ![]() ,
, ![]() равны
равны
![]() ,
, ![]() , (8.11)
, (8.11)
где ![]() .
.
Т.е. мера ![]() является суммой взвешенных сумм количеств внешних и внутренних ссылочных понятий, используемых во всех модулях библиотеки L, а мера
является суммой взвешенных сумм количеств внешних и внутренних ссылочных понятий, используемых во всех модулях библиотеки L, а мера ![]() - той же суммой, но усредненной по количеству Mмодулей в библиотеке L.
- той же суммой, но усредненной по количеству Mмодулей в библиотеке L.
8.7. Меры сложности ![]() ,
, ![]() базируются на контекстно-независимой мере сложности модуля
базируются на контекстно-независимой мере сложности модуля ![]() (см. Утверждение 7.3). Аналогично мерам
(см. Утверждение 7.3). Аналогично мерам ![]() ,
, ![]() имеем
имеем
![]() ,
, ![]() . (8.12)
. (8.12)
Мера ![]() представляет собой сумму диаметров всех модулей библиотеки L, а мера
представляет собой сумму диаметров всех модулей библиотеки L, а мера ![]() - ту же сумму, но усредненную по количеству модулей в библиотеке L.
- ту же сумму, но усредненную по количеству модулей в библиотеке L.
Меры ![]() ,
, ![]() для библиотеки
для библиотеки ![]() имеют следующие значения:
имеют следующие значения:
![]() ,
, ![]() ;
;
![]() ,
, ![]() .
.
8.8. Меры сложности ![]() ,
, ![]() формируются на основе контекстно-независимой меры сложности модуля
формируются на основе контекстно-независимой меры сложности модуля ![]() (см. Утверждение 7.4). Подобно мерам
(см. Утверждение 7.4). Подобно мерам ![]() ,
, ![]() имеем
имеем
![]() ,
, ![]() . (8.13)
. (8.13)
Мера ![]() - это сумма реберных плотностей всех модулей библиотеки L, а мера
- это сумма реберных плотностей всех модулей библиотеки L, а мера ![]() - та же сумма, но усредненную по количеству модулей в библиотеке L.
- та же сумма, но усредненную по количеству модулей в библиотеке L.
Для библиотеки ![]() меры
меры ![]() ,
, ![]() имеют следующие значения:
имеют следующие значения:
![]() (см. п. 7.4),
(см. п. 7.4), ![]() ;
;
![]() ,
, ![]() .
.
8.9. Меры сложности ![]() ,
, ![]() формируются на основе контекстно-зависимой мультимеры
формируются на основе контекстно-зависимой мультимеры ![]() (см. п. 7.5) и равны
(см. п. 7.5) и равны
![]() ,
, ![]() . (8.14)
. (8.14)
Мера ![]() есть ни что иное, как сумма аддитивных сверток мер
есть ни что иное, как сумма аддитивных сверток мер ![]() -
- ![]() всех модулей библиотеки L, а мера
всех модулей библиотеки L, а мера ![]() - та же сумма сверток, но усредненная по количеству модулей в библиотеке L.
- та же сумма сверток, но усредненная по количеству модулей в библиотеке L.
9. Прочие меры сложности библиотек модулей
Меры сложности библиотеки L, рассматриваемые в данном разделе, в основном сконструированы на основе мер сложности информационно-логического графа библиотеки ![]() - графа информационных связей модулей
- графа информационных связей модулей ![]() ,
, ![]() .
.
9.1. Меры сложности ![]() ,
, ![]() строятся на основе взвешенной суммы количества вершин и кратностей дуг в графе
строятся на основе взвешенной суммы количества вершин и кратностей дуг в графе ![]() :
:
![]() ,
, ![]() ,
,![]() ; (9.1)
; (9.1)
![]() . (9.2)
. (9.2)
Здесь ![]() - множитель, определяющий относительный вес количества вершин и кратностей дуг;
- множитель, определяющий относительный вес количества вершин и кратностей дуг; ![]() , если модули
, если модули ![]() ,
, ![]() не имеют информационных связей.
не имеют информационных связей.
В качестве примера в данном и последующих пунктах рассматривается библиотека ![]() , ЯПФ графа информационных связей модулей которой
, ЯПФ графа информационных связей модулей которой ![]() представлена на Рис. 9.1. В этом графе
представлена на Рис. 9.1. В этом графе ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

Рис. 9.1. Пример графа информационных связей модулей ![]() (в форме ЯПФ).
(в форме ЯПФ).
В предположении, что ![]() , для библиотеки
, для библиотеки ![]() имеем:
имеем:
![]() ;
; ![]() .
.
9.2. Меры сложности ![]() ,
, ![]() представляют собой высоту и усредненную высоту графа
представляют собой высоту и усредненную высоту графа ![]() , соответственно:
, соответственно:
![]() ,
, ![]() . (9.3)
. (9.3)
Для библиотеки ![]() имеем:
имеем:
![]() ;
; ![]() .
.
9.3. Меры сложности ![]() ,
, ![]() - реберная плотность и усредненная реберная плотность графа
- реберная плотность и усредненная реберная плотность графа ![]() , соответственно:
, соответственно:
![]() ,
, ![]() . (9.4)
. (9.4)
Для библиотеки ![]() имеем:
имеем:
![]() ;
; ![]() .
.
9.4. Меры сложности ![]() ,
, ![]() - общее количеству контуров в графе
- общее количеству контуров в графе ![]() и их усредненное количество
и их усредненное количество
![]() ,
, ![]() . (9.5)
. (9.5)
9.5. Меры сложности ![]() ,
, ![]() представляют собой общее количество кратных понятий в библиотеке L и то же количество, но усредненное по количеству модулей в библиотеке, соответственно:
представляют собой общее количество кратных понятий в библиотеке L и то же количество, но усредненное по количеству модулей в библиотеке, соответственно:
![]() ,
, ![]() ,
, ![]() ; (9.6)
; (9.6)
![]() . (9.7)
. (9.7)
Отметим, что в каждой из сумм (9.6) величина ![]() , если понятие
, если понятие ![]() имеет кратность, равную единице, т.е. ни разу не повторено в библиотеке L.
имеет кратность, равную единице, т.е. ни разу не повторено в библиотеке L.
9.6. Мультимеры ![]() ,
, ![]() - аддитивная свертка мер
- аддитивная свертка мер ![]() -
- ![]() и мер
и мер ![]() ,
, ![]() , соответственно:
, соответственно:
![]() ;
; ![]() . (9.8)
. (9.8)
Здесь для простоты записи опущены весовые множители в выражениях для мер ![]() ,
, ![]() ,
, ![]() ,
, ![]() , а также для мер
, а также для мер ![]() ,
, ![]() ,
, ![]() ,
, ![]() ; вектор весовых множителей
; вектор весовых множителей ![]() ;
; ![]() ,
, ![]() .
.
Замечание 9.1. Аналогично мерам сложности модулей, каждая из рассмотренных мер сложности библиотеки может служить также мерой его усвояемость (см. замечание 7.1). Особенно естественно использовать в качестве такого критерия меры ![]() ,
,![]() ,
, ![]() ,
, ![]() . Использование в этом качестве мер
. Использование в этом качестве мер ![]() ,
,![]() мы обсуждали в Замечании 7.1. Основания для использования в качестве критерия усвояемости мер
мы обсуждали в Замечании 7.1. Основания для использования в качестве критерия усвояемости мер ![]() ,
, ![]() аналогичны: контуры значительно затрудняют восприятие учебного материала субъектом обучения, и наличие их значительного количества приводит к низкой усвояемости этого материала. Отдельного обсуждения заслуживают также меры
аналогичны: контуры значительно затрудняют восприятие учебного материала субъектом обучения, и наличие их значительного количества приводит к низкой усвояемости этого материала. Отдельного обсуждения заслуживают также меры ![]() ,
, ![]() . Кроме мер сложности библиотеки L, эти меры могут служить мерой гибкости (адаптивности) этой библиотеки. Действительно, большие значения этих мер говорят о большом количестве кратных понятий в библиотеке, а значит и о большом количестве дублирующих модулей. Именно такие модули являются основой для построения индивидуальных учебных курсов
. Кроме мер сложности библиотеки L, эти меры могут служить мерой гибкости (адаптивности) этой библиотеки. Действительно, большие значения этих мер говорят о большом количестве кратных понятий в библиотеке, а значит и о большом количестве дублирующих модулей. Именно такие модули являются основой для построения индивидуальных учебных курсов![]()
В заключение разделов 8, 9 приведем рекомендации по применению рассмотренных мер сложности библиотеки. Из соображений простоты интерпретации и минимума вычислительной сложности рекомендуется использовать меры ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() или те же, но усредненные меры
или те же, но усредненные меры ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Т.е. рекомендуется использовать следующие меры:
. Т.е. рекомендуется использовать следующие меры:
· меры на основе количеств входных и выходных понятий модулей библиотеки (меры ![]() ,
, ![]() );
);
· меры на основе количеств внешних и внутренних ссылочных понятий тех же модулей (меры ![]() ,
, ![]() );
);
· меры на основе реберных плотностей графов ![]() (меры
(меры ![]() ,
, ![]() );
);
· меры на основе количества вершин и кратностей дуг в графе ![]() (меры
(меры ![]() ,
, ![]() );
);
· меры на основе реберной плотности графа ![]() (меры
(меры ![]() ,
, ![]() );
);
· меры на основе количества кратных понятий в библиотеке L (меры ![]() ,
, ![]() )).
)).
Другими словами, рекомендуется использовать мультимеры ![]() ,
, ![]() при
при ![]() ,
, ![]() .
.
10. Меры сложности учебных курсов
В качестве мер сложности учебного курса ![]() можно использовать меры, аналогичные мерам
можно использовать меры, аналогичные мерам ![]() -
- ![]() библиотеки L, а также меры, аналогичные мерам
библиотеки L, а также меры, аналогичные мерам ![]() -
- ![]() . Поскольку корректно построенный учебный курс не должен содержать кратных понятий, меры, аналогичные мерам
. Поскольку корректно построенный учебный курс не должен содержать кратных понятий, меры, аналогичные мерам ![]() ,
, ![]() , в этом списке отсутствуют.
, в этом списке отсутствуют.
Таким образом, в качестве мер сложности учебного курса ![]() можно использовать меры
можно использовать меры ![]() -
- ![]() и меры
и меры ![]() -
- ![]() . Можно использовать также мультимеры, аналогичные мультмерам (9.8):
. Можно использовать также мультимеры, аналогичные мультмерам (9.8):
![]() ;
; ![]() . (10.1)
. (10.1)
Здесь для простоты записи опущены весовые множители в выражениях для мер ![]() ,
, ![]() ,
, ![]() ,
, ![]() , а также для мер
, а также для мер ![]() ,
, ![]() ,
, ![]() ,
, ![]() ; вектор весовых множителей
; вектор весовых множителей ![]() ;
; ![]() ,
, ![]() .
.
Непосредственно использовать введенные меры может быть методически ошибочным. Дело в том, что, очевидно, сложность учебного курса зависит еще и от количества времени, которое выделено на его изучение. Обозначим это время ![]() , и наряду с введенными мерами будем использовать их нормированные варианты:
, и наряду с введенными мерами будем использовать их нормированные варианты:
![]() ,
, ![]() ;
; 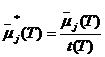 ; (10.2)
; (10.2)
![]() ,
,  . (10.2)
. (10.2)
Для введенных мер сложности учебного курса ![]() остается справедливым замечание 9.1, а также рекомендации по их применению, изложенные в конце п. 9.
остается справедливым замечание 9.1, а также рекомендации по их применению, изложенные в конце п. 9.
Заключение
Некоторые из мер сложности, предложенные в работе, могут быть использованы в качестве мер усвояемости учебного материала и мер его адаптивности. Это обстоятельство позволяет формально ставить задачу оценки качества учебных материалов, как трехкритериальную задачу (с критериями: сложность; усвояемость;, адаптивность). Результаты работы позволяют значения всех трех критериев качества вычислить автоматически, только на основе анализа семантической сети соответствующего учебного материала.
Все меры, рассмотренные в работе, построены только на основе соответствующей семантической сети. Наряду с этим можно предложить и другие меры, например: меры, использующие объемы модулей, библиотек и учебных курсов; меры использующие метаданные тех же единиц контента и др. С нашей точки зрения меры такого сорта менее содержательны и объективны, чем меры, на основе метрик семантической сети.
Для многих мер, предложенных в работе, можно предложить их варианты, построенные на основе шенноновской меры информации.
Литература
1. Official ADL SCORM overview //http://www.adlnet.gov/scorm
2. Норенков И.П. технология разделяемых единиц контента для создания и сопровождения информационно-образовательных сред //Информационные технологии, 2003, ╧ 8.
3. Белоусова Л.И., Колгатин А.Г., Колгатина Л.С. Принципы построения автоматизированной системы педагогической диагностики //УСиМ, 2007, ╧ 2, с. 75 – 81.
4. Креативная педагогика: методология, теория, практика /под ред. Ю.Г.Круглова. –М.:МГОПУ им. М.А.Шолохова, изд. центр «Альфа», 2002. -240 с.
5. Карпенко А.П., Соколов Н.К. Контроль понятийных знаний субъекта обучения с помощью когнитивных карт //Управление качеством инженерного образования и инновационные образовательные технологии. Сборник докладов Международной научно-методической конференции 28-30 октября 2008 г. –М.:МГТУ им. Н.Э.Баумана, 2008, Ч.2, с. 55-57.
6. Программный продукт «Сеть научных понятий» // http://www.websamba.com/supertest
7. Добряков А.А., Милова В.М. Экспертно-аналитический метод оценки качества образовательных систем на основе нечетко-множественного подхода //Качество. Инновации. Образование. 2007., ╧1, с. 36 -41.
8. Галямова Е.В. Оценка качества электронного учебного материала //Управление качеством инженерного образования и инновационные образовательные технологии. Сборник докладов Международной научно-методической конференции 28-30 октября 2008 г. –М.:МГТУ им. Н.Э.Баумана, 2008, Ч.2, с. 29-34.
9. Усачев Ю.Е. Проектирование интеллектуального учебника // http://www.e-joe.ru/sod/00/4_00/us.html
10. Рабинович П.Д. Исследование и разработка моделей, алгоритмов и программного обеспечения в компьютерных обучающих системах. Автореферат диссертации на соискание ученой степени кандидата технических наук. –Москва, 2005.
11. Норенков И.П., Уваров М.Ю. База и генератор образовательных ресурсов //Информационные технологии, 2005, ╧9, с. 60-65.
12. Федотов И.Е. Некоторые приемы параллельного программирования: Учебное пособие. - М.: Изд-во МГИРЭА(ТУ), 2008. - 188 с.
13. Евстигнеев В.А. Применение теории графов в программировании. –М.: Наука, 1985. -332 с.
14. Ларичев О.И. Теория и методы принятия решений, а также Хроника событий в Волшебных странах. – М.: Университетская книга, Логос, 2006. -292 с.
15. Карпенко А.П., Федорук В.Г. Обзор программных систем многокритериальной оптимизации. Отечественные системы //Информационные технологии, 2008, ╧1, с. 15-22.
16. Вентцель Е.С. Исследование операций: задачи, принципы, методология. – М.: Дрофа, 2006. -206 с.
17. Белоус В.В., Васильев Н.В., Карпенко А.П. Вопросы регистрации электронных изданий //Управление качеством инженерного образования и инновационные образовательные технологии. Сборник докладов Международной научно-методической конференции 28-30 октября 2008 г. –М.:МГТУ им. Н.Э.Баумана, 2008, Ч.2, с.45-50.
Публикации с ключевыми словами: обучающая система, семантическая сеть, разделяемая единица контента, мера сложности
Публикации со словами: обучающая система, семантическая сеть, разделяемая единица контента, мера сложности
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



