научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 10, октябрь 2008
УДК 004.422.6
К.А.Пасечников
При решении задач структурного синтеза структуры данных используются для хранения не только основной (информации о графе), но и различной вспомогательной информации. Как было показано в [2,3], способ организации элементов структуры данных существенно влияет на вычислительную и ёмкостную сложность программы решения задач структурного синтеза. Следовательно, для решения ряда задач, одной из которых является задача синтеза оптимальных структур данных, необходимо разработать такую модель структуры данных, которая отражает структурные особенности различных способов хранения данных, существенные с точки зрения оценки вычислительной сложности операций, выполняемых над структурой данных, а также ёмкостной сложности структуры данных.
Любая структура данных представляет собой описание одного
из возможных способов размещения конечного множества данных D в памяти. При этом каждому элементу множества данных
ставится во взаимнооднозначное соответствие P
адрес из множества доступных адресов памяти ![]() .
.
Структура данных кроме полезной информации в виде
элементов данных зачастую хранит служебную информацию о связях элементов между
собой. Элемент данных вместе со служебной информацией будем далее называть
компонентом структуры данных. Таким образом можно говорить о наличии множества С
компонентов структуры данных и множества Z,
определяющего взаимнооднозначное соответствие размещенных элементов данных
компонентам структуры ![]() . Для учёта связей между компонентами
структуры данных введём однозначное соответствие
. Для учёта связей между компонентами
структуры данных введём однозначное соответствие ![]() .
.
На данный момент при построении сложных структур данных применяется два основных способа организации данных - векторный и списковый.
Векторный способ организации предполагает последовательное размещение однотипных (одинаковых по размеру) элементов в непрерывной области памяти. Подобное размещение позволяет определить адрес любого элемента вектора по его номеру, адресу первого элемента и размеру. При этом адрес текущего элемента можно определить по адресу любого элемента, находящегося слева или справа от него. Элементом вектора может быть: элемент данных, указатель на данные или структуру данных, ключ для получения данных (в это случае данные хранятся отдельно), признак или флаг (характеристические вектора).
Компонентом вектора будет являться элемент данных, а
множество связей компонентов F будет
представлять собой декартово произведение множества С самого на себя,
т.е. ![]() .
.
При переходе от объекта к модели поставим во
взаимнооднозначное соответствие множеству D
множество вершин графа XD, а
множеству адресов A - множество вершин графа XА. Поскольку множество P описывает взаимнооднозначное отношение между
множествами A и D,
каждой паре элементов множества P, можно
поставить в соответствие либо две ориентированных дуги, либо одно
неориентированное ребро. Из соображений простоты выбираем второй вариант –
сопоставляем ребро ![]() . Таким образом, каждому компоненту вектора с
будет взаимнооднозначно соответствовать двухвершинный подграф с одним ребром
. Таким образом, каждому компоненту вектора с
будет взаимнооднозначно соответствовать двухвершинный подграф с одним ребром
![]() .
.
Каждой связи компонентов из множества F сопоставим дугу из множества UF (см. рисунок 1).

Рисунок 1 - Модель вектора
Рассмотрим способ определения ёмкостной сложности вектора
по модели. Поскольку вектор предназначен для хранения данных фиксированной
длины, обозначим размер одного элемента через ![]() . Количество данных, хранимых
вектором, определяется мощностью множества XА.
Исходя из этого, сопоставим каждому элементу из этого множества значение веса,
равное
. Количество данных, хранимых
вектором, определяется мощностью множества XА.
Исходя из этого, сопоставим каждому элементу из этого множества значение веса,
равное ![]() ,
т.е.
,
т.е. ![]() .
Также каждому элементу множества XD
сопоставим значение веса, равное нулю, т.е.
.
Также каждому элементу множества XD
сопоставим значение веса, равное нулю, т.е. ![]() . В результате, объём памяти,
требуемый для хранения вектора, составит:
. В результате, объём памяти,
требуемый для хранения вектора, составит:
![]()
При сравнении нескольких структур данных между собой
необходимо знать объём памяти ![]() , занимаемый вспомогательными элементами
каждой структуры данных в зависимости от количества хранимых элементов данных.
Далее функцию
, занимаемый вспомогательными элементами
каждой структуры данных в зависимости от количества хранимых элементов данных.
Далее функцию ![]() будем называть дополнительной ёмкостной
сложностью. Очевидно, что функция
будем называть дополнительной ёмкостной
сложностью. Очевидно, что функция ![]() будет связана будет связана с
будет связана будет связана с ![]() следующим
соотношением:
следующим
соотношением:
![]()
Соответственно для вектора ![]() .
.
Рассмотрим особенности подсчёта функциональной вычислительной сложности по предлагаемой модели вектора. Для определения адреса произвольного элемента по адресу текущего элемента необходимо найти дугу из множества UF инцидентную вершинам адреса текущего и искомого элементов. Подграф g(XА,UF) является полным, что позволяет на основании адреса данного элемента определить адрес любого элемента вектора за O(1). Можно показать, что вычислительная сложность операций, посчитанная по модели, совпадает с вычислительной сложностью операций над вектором, приведённой в [1,2], что доказывает адекватность полученной модели.
Для дополнения модели информацией о вычислительной
сложности операций определим также множество функций ![]() как:
как:
![]()
где
S = { ![]() } – множество
допустимых операций над структурой данных,
} – множество
допустимых операций над структурой данных,
![]() - функция оценки вычислительной сложности i-ой операции.
- функция оценки вычислительной сложности i-ой операции.
Таким образом, модель вектора будет выглядеть следующим образом:
![]()
где
![]() - смешанный граф, описывающий организацию
элементов,
- смешанный граф, описывающий организацию
элементов,
![]() - множество функций, определяющих
вычислительную сложность операций,
- множество функций, определяющих
вычислительную сложность операций,
![]() - дополнительная ёмкостная сложность
структуры данных.
- дополнительная ёмкостная сложность
структуры данных.
Полученная модель позволяет задавать не только способ организации элементов, но и временные и ёмкостные параметры структуры данных.
Ограничения, присущие векторному способу организации данных, делают его использование нерациональным в тех случаях, когда число элементов в структуре данных заранее неизвестно. В этом случае оптимальным вариантом является применение списковой организации данных. Основными структурами со списковой организацией данных, применяемыми для представления графовых моделей и вспомогательных данных, являются линейные односвязные, линейные двусвязные, n-связные и древовидные списки. С точки зрения реализации n-связные списки являются комбинацией списков и векторов адресов элементов, а потому их модели строятся с использованием моделей этих структур.
Списковая организация данных подразумевает
размещение элементов списка в произвольных свободных участках памяти. При
построении списковых структур с каждым компонентом списка связывается набор
вспомогательных полей, обеспечивающий связь отдельных компонентов списка между
собой. Так, для линейного односвязного списка компоненты связаны между собой
отношением «предыдущий-следующий» за счет хранения в компоненте адреса
следующего компонента. Наличие вспомогательных полей требует введения
дополнительных множеств – множество ![]() , представляющее собой множество вспомогательных
элементов данных (указателей) и множество
, представляющее собой множество вспомогательных
элементов данных (указателей) и множество ![]() , представляющее собой множество
адресов вспомогательных элементов данных. Аналогично необходимо ввести
множества
, представляющее собой множество
адресов вспомогательных элементов данных. Аналогично необходимо ввести
множества ![]() и
и
![]() , служащие
для определения связей между вспомогательными элементами и элементами данных.
, служащие
для определения связей между вспомогательными элементами и элементами данных.
Рассмотрим модель простейшего односвязного списка, когда с каждым элементом списка связан всего один элемент данных. Список может хранить все те же данные, что и вектор за исключением того, что элементы данных списка не обязательно должны быть однотипными. При переходе от объекта к модели будем считать, что каждый компонент списка представляет собой запись, а сам список является множеством записей, соединённых между собой. Записью называют разновидность вектора, основными отличиями которой являются заранее известное постоянное количество элементов и отсутствие требования однотипности (одноразмерности) элементов данных.
Отобразим множество компонентов списка С на
множество записей H следующим образом – количество
элементов каждой записи множества H для
односвязного списка должно быть равно двум, то есть ![]() , множество
, множество ![]() взаимнооднозначно
отображается на множество первых элементов данных (
взаимнооднозначно
отображается на множество первых элементов данных (![]() ), множество D – на множество вторых элементов данных (
), множество D – на множество вторых элементов данных (![]() ).
Аналогично отображаются множества A и
).
Аналогично отображаются множества A и ![]() на
на ![]() ,
,![]() . Связи элементов
внутри записи представим в виде множества UА.
Множества P и
. Связи элементов
внутри записи представим в виде множества UА.
Множества P и ![]() отображаются на множества дуг UАD, UAD’. Таким образом,
множество С взаимнооднозначно отображается на множество H, представляющее собой множество подграфов
отображаются на множества дуг UАD, UAD’. Таким образом,
множество С взаимнооднозначно отображается на множество H, представляющее собой множество подграфов ![]() . Связи
компонентов между собой, задаваемые множеством F
отобразим на множество дуг UF (см.
рисунок 2).
. Связи
компонентов между собой, задаваемые множеством F
отобразим на множество дуг UF (см.
рисунок 2).
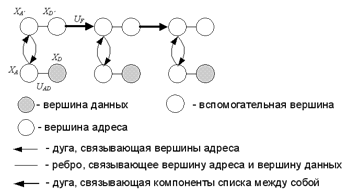
Рисунок 2 – Модель односвязного списка
Расчёт ёмкостной сложности списка сводится к подсчёту памяти, занимаемой всеми компонентами списка:

Если список хранит однотипные элементы, а размер одного
указателя равен ![]() байт, то:
байт, то:

По аналогии с вектором, модель списка будет выглядеть следующим образом:
 - смешанный граф, описывающий организацию
элементов,
- смешанный граф, описывающий организацию
элементов,
![]() - множество функций, определяющих
вычислительную сложность операций,
- множество функций, определяющих
вычислительную сложность операций,
![]() - дополнительная ёмкостная сложность списка.
- дополнительная ёмкостная сложность списка.
Полученные модели базовых структур данных позволяют определить организацию элементов данных; отражают ёмкостные и временные параметры структуры данных; позволяют создавать сложные комбинированные структуры данных, а также дают возможность автоматизировать процесс определения их временных и ёмкостных параметров.
Литература
1. Т. Кормен, Ч. Лейзерсон, Р. Ривест. Алгоритмы: построение и анализ. – М.:МЦНМО, 2004. – 960 с.
2. В.А. Овчинников. Алгоритмизация комбинаторно-оптимизационных задач при проектировании ЭВМ и систем. – изд-во. М.:МГТУ им. Баумана, 2001. – 288 с.
3. А. Ахо, Д. Ульман, Д. Хопкрофт. Структуры данных и алгоритмы. – М.:Вильямс, 2003. – 384 с.
4. Jiazhen Cai, Robert Paige. Type Analysis and Data Structure Selection. – Computer Sci. Dept., Courant Inst. Math. Sci., New York Univ. , 1973. – 520 pp.
5. Пасечников К.А. Анализ проблемы синтеза оптимальных структур данных для алгоритмов решения комбинаторных задач на графах. . Сборник трудов #5 молодых учёных, аспирантов и студентов ²Информатика и системы управления в ХХI веке⌡, . М.: МГТУ им. Н.Э. Баумана, 2007. 415 с.
6. Пасечников К.А., Иванова Г.С. Модели структур данных для представления объектов задач структурного анализа и синтеза. - Сборник трудов #4 молодых учёных, аспирантов и студентов "Информатика и системы управления", - М.: МГТУ им. Баумана, 2006. - 154 с.
7. Овчинников В.А., Иванова Г.С., Ничушкина Т.Н. Выбор структур данных для представления графов при решении комбинаторно-оптимизационных задач // Вестник Московского государственного технического университета им. Н.Э. Баумана. Приборостроение. . 2001. . # 2(43). . C. 39-51.
8. Иванова Г.С, Пасечников К.А. Макрогенерация описаний структур данных для системы проектирования алгоритмов решения задач структурного синтеза // Современные информационные технологии: Сб. трудов каф., посвященный 175-летию МГТУ им. Н.Э. Баумана. . М.: Эликс+, 2004. . С. 69-73.
Публикации с ключевыми словами: оптимизация, структуры данных
Публикации со словами: оптимизация, структуры данных
Смотри также:
- Возможности применения параллельных методов вычисления в системе программирования на языке S-FLOGOL
- Разработка программной среды для моделирования и оптимизации складской политики двухэшелонных многопродуктовых цепей поставки
- Математическая модель взаимодействия предприятий по производству продуктов питания молочной отрасли АПК РФ
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



