научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 10, октябрь 2008
УДК 621.983; 539.374
Дериева А.Н., Агеева А.И.
ГОУ ВПО «ТулГУ»
Кафедра «Механика
пластического формоизменения»
Научный руководитель: д.т.н., проф.. Яковлев С.П.
Рассмотрена операция вытяжки с утонением стенки осесимметричной толстостенной цилиндрической заготовки. Материал заготовки жесткопластический, обладает цилиндрической анизотропией механических свойств [1]. Течение материала принимается осесимметричным. Анализ процесса вытяжки с утонением стенки реализуется в цилиндрической системе координат. Схема к анализу вытяжки с утонением стенки приведена на рис. 1. Течение материала принимается установившимся. Принимаем, что условия трения на контактной поверхности инструмента с заготовкой подчиняется закону Кулона
![]() ;
; ![]() ,
,
где ![]() и
и ![]() - коэффициенты
трения на контактных поверхностях матрицы и пуансона;
- коэффициенты
трения на контактных поверхностях матрицы и пуансона; ![]() и
и ![]() - нормальные напряжения
на контактных поверхностях матрицы и пуансона соответственно.
- нормальные напряжения
на контактных поверхностях матрицы и пуансона соответственно.

Рис. 1. Схема к анализу вытяжки с утонением стенки
Условие несжимаемости материала позволяет установить связь между скоростью течения материала на входе в очаг деформации и выходе из очага деформации:
![]() .
(1)
.
(1)
Компоненты
осевой ![]() и
радиальной
и
радиальной ![]() скоростей
течения могут быть определены по выражениям:
скоростей
течения могут быть определены по выражениям:
 ;
; 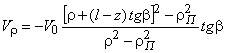 , (2)
, (2)
где ![]() .
.
Скорости
деформаций рассчитываются по выражениям, полученным с учетом соотношений (2),
условия несжимаемости материала ![]() , следующим образом:
, следующим образом:
|
|
(3) |
где
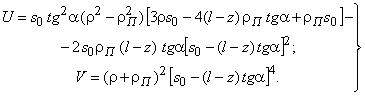
Величина
интенсивности скоростей деформаций ![]() вычисляется по выражению [2]:
вычисляется по выражению [2]:
|
|
(4) |
где ![]() ;
; ![]() ;
; ![]() ; F,
G, H, M - параметры
анизотропии.
; F,
G, H, M - параметры
анизотропии.
Выражение
(4) позволяет определить распределение интенсивностей скоростей деформаций
вдоль ряда (![]() )
траекторий течения материала.
)
траекторий течения материала.
Накопленная интенсивность деформации вдоль траектории с учётом добавки деформации, связанной с изменением поворота траектории частицы материала при входе в очаг деформации, определяется по выражению:
 . (5)
. (5)
Если нужно определить накопленную интенсивность деформации в заготовке после деформации, то следует к рассчитанной величине добавить ещё второй член к выражению (5) на выходе из очага деформации.
Имея
в своем распоряжении кривую упрочнения материала, находим среднюю величину интенсивности
напряжения ![]() в очаге деформации по формуле
в очаге деформации по формуле
![]() , (6)
, (6)
где ![]() ,
, ![]() и
и ![]() - параметры кривой упрочнения;
- параметры кривой упрочнения; ![]() - средняя величина интенсивности
деформации в очаге деформации.
- средняя величина интенсивности
деформации в очаге деформации.
Для определения напряжений в очаге деформации располагаем уравнениями теории пластического течения анизотропного материала
|
|
(7) |
и уравнениями равновесия в цилиндрической системе координат [3]
![]() ;
; ![]() ;
; ![]() , (8)
, (8)
где ![]() - нормальные и
касательное напряжения, являющиеся функциями
- нормальные и
касательное напряжения, являющиеся функциями ![]() и
и ![]() .
.
Рассмотрим
третье уравнение равновесия из системы (8). Используя соотношения (7) и
выражение для определения ![]() , получим
, получим
|
|
(9) |
где
![]() ;
; ![]()
![]()
![]()


 .
.
Представим
приведенное выше уравнение в виде конечных разностей. Для интегрирования этого
уравнения нужно сформулировать граничные условия. В соответствии с выбранной
кинематикой течения на входе в очаге деформации и выходе из него происходит
резкое изменение направления течения от вертикального до наклонного к осевой
под углом ![]() ,
что связано с разрывом тангенциальной составляющей скорости течения
,
что связано с разрывом тангенциальной составляющей скорости течения ![]() . Изменение
направления течения учитывается путем коррекции осевого напряжения на границе
очага деформации по методу баланса мощностей следующим образом:
. Изменение
направления течения учитывается путем коррекции осевого напряжения на границе
очага деформации по методу баланса мощностей следующим образом:
![]() . (10)
. (10)
Заметим,
что угол ![]() на
входе в очаг деформации определяется по формуле
на
входе в очаг деформации определяется по формуле ![]() , а при выходе из очага деформации
так
, а при выходе из очага деформации
так ![]() .
.
Соотношение
(10) будет граничным условием для уравнения (9) при ![]() . Компоненты напряжений
. Компоненты напряжений ![]() ,
, ![]() и
и ![]() определяются из
уравнений (7).
определяются из
уравнений (7).
Составляющая
силы ![]() для
преодоления трения на матрице находится по выражению:
для
преодоления трения на матрице находится по выражению:
![]() .
.
Сила, разгружающая стенку изделия, определяется по формуле
![]() .
.
Сила, передающаяся на стенку изделия, вычисляется так
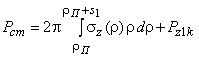 ,
,
а сила операции вытяжки определяется следующим образом
 ,
,
где ![]() ;
; ![]() ;
;  .
.
Величину
![]() находим
по формуле преобразования компонент напряжений при переходе от одной системы
координат к другой
находим
по формуле преобразования компонент напряжений при переходе от одной системы
координат к другой
![]() .
.
Приведенные выше соотношения могут быть использованы для оценки кинематики течения материала, напряженного и деформированного состояний, силовых режимов и предельных возможностей вытяжки с утонением стенки толстостенных цилиндрических заготовок из анизотропных материалов.
Расчеты выполнены для операции вытяжки
с утонением стенки толстостенных цилиндрических заготовок из ряда материалов,
механические свойства которых приведены в табл. 1, при следующих геометрических
размерах заготовки: ![]() мм;
мм; ![]() =40 мм.
=40 мм.
Таблица 1
Механические характеристики исследуемых материалов
|
Материал |
|
МПа |
|
|
|
|
|
Сталь 08 кп |
268,66 |
329,5 |
0,478 |
0,817 |
0,783 |
2,999 |
|
Латунь Л63 |
214,94 |
509,07 |
0,575 |
0,666 |
0,750 |
2,479 |
|
Алюминиевый сплав АМг6М |
29,20 |
151,83 |
0,440 |
0,67 |
0,540 |
2,805 |
Продолжение табл. 1
|
Материал |
|
|
|
|
|
|
Сталь 08 кп |
1,791 |
-0,946 |
0,471 |
0,169 |
0,143 |
|
Латунь Л63 |
4,640 |
-0,769 |
0,793 |
-0,279 |
-0,246 |
|
Алюминиевый сплав АМг6М |
2,148 |
-1,230 |
0,417 |
0,217 |
0,338 |
Графические
зависимости изменения относительной величины силы процесса ![]() от угла
конусности матрицы
от угла
конусности матрицы ![]() при вытяжке с утонением стенки
полых цилиндрических заготовок из стали 08 кп представлены на рис. 2 (
при вытяжке с утонением стенки
полых цилиндрических заготовок из стали 08 кп представлены на рис. 2 (![]() ).
).

Рис. 2. Графические зависимости изменения ![]() от
от ![]() :
:
(![]() ;
; ![]() )
)
Анализ
графиков и результатов расчета показывает, что с увеличением угла конусности
матрицы ![]() ,
уменьшением коэффициента утонения
,
уменьшением коэффициента утонения ![]() и относительной величины
и относительной величины ![]() , увеличением коэффициентов
трения на контактной поверхности матрицы
, увеличением коэффициентов
трения на контактной поверхности матрицы ![]() и пуансона
и пуансона ![]() относительная величина
осевого напряжения
относительная величина
осевого напряжения ![]() возрастает.
Установлено, что при вытяжке с утонением стенки толстостенных заготовок существуют
оптимальные углы конусности матрицы в пределах 12¼18°,
соответствующие наименьшей величине силы. Показано, что с увеличением
коэффициента утонения
возрастает.
Установлено, что при вытяжке с утонением стенки толстостенных заготовок существуют
оптимальные углы конусности матрицы в пределах 12¼18°,
соответствующие наименьшей величине силы. Показано, что с увеличением
коэффициента утонения ![]() и отношения
и отношения ![]() , уменьшением коэффициентов
трения на контактной поверхности матрицы
, уменьшением коэффициентов
трения на контактной поверхности матрицы ![]() и пуансона
и пуансона ![]() относительная величина
силы
относительная величина
силы ![]() уменьшается.
уменьшается.
Предельные
степени деформации вытяжки с утонением стенки определялись по максимальной величине
растягивающего напряжения ![]() с учетом упрочнения на выходе из
очага пластической деформации (первый критерий)
с учетом упрочнения на выходе из
очага пластической деформации (первый критерий)
![]() ,
, ![]() (11)
(11)
и по величине степени использования ресурса (второй критерий)
![]() . (12)
. (12)
Величина
предельной интенсивности деформации ![]() находится по выражению
находится по выражению
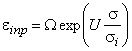
![]() , (13)
, (13)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() - константы материала, определяемые
в зависимости от рода материала согласно работам В.Л. Колмогорова и А.А.
Богатова и уточняющиеся из опытов на растяжение образцов в условиях плоского
напряженного состояния в зависимости от анизотропии механических свойств
ортотропного тела;
- константы материала, определяемые
в зависимости от рода материала согласно работам В.Л. Колмогорова и А.А.
Богатова и уточняющиеся из опытов на растяжение образцов в условиях плоского
напряженного состояния в зависимости от анизотропии механических свойств
ортотропного тела; ![]() ,
, ![]() ,
, ![]() - углы между первой главной осью
напряжений и главными осями анизотропии;
- углы между первой главной осью
напряжений и главными осями анизотропии; ![]() - среднее напряжение;
- среднее напряжение; ![]() .
.
Интегрирование
в выражении (12) ведется по траектории течения материала. До деформации ![]() . Разрушение
будет иметь место при
. Разрушение
будет иметь место при ![]() . В зависимости от условий
эксплуатации или последующей обработки изготовляемого изделия уровень
повреждаемости не должен превышать величины
. В зависимости от условий
эксплуатации или последующей обработки изготовляемого изделия уровень
повреждаемости не должен превышать величины ![]() . При назначении величин степеней
деформации в процессе пластического формоизменения следует учитывать рекомендации
по степени использования запаса пластичности В.Л. Колмогорова и А.А. Богатова,
согласно которым для ответственных деталей, работающих и подвергающихся после
обработки давлением термической обработке (отжигу или закалке), допустимой величиной
степени использования запаса пластичности следует считать
. При назначении величин степеней
деформации в процессе пластического формоизменения следует учитывать рекомендации
по степени использования запаса пластичности В.Л. Колмогорова и А.А. Богатова,
согласно которым для ответственных деталей, работающих и подвергающихся после
обработки давлением термической обработке (отжигу или закалке), допустимой величиной
степени использования запаса пластичности следует считать ![]() , а для неответственных
деталей допустимая степень использования запаса пластичности может быть принята
, а для неответственных
деталей допустимая степень использования запаса пластичности может быть принята
![]() [4-6].
[4-6].
Приведенные
выше неравенства (11) и (12) не разрешаются в явном виде относительно
предельного коэффициента утонения ![]() , поэтому зависимости предельного
коэффициента утонения
, поэтому зависимости предельного
коэффициента утонения ![]() от технологических параметров
процесса вытяжки с утонением стенки полых цилиндрических деталей из анизотропных
материалов устанавливались путем численных расчетов по этим неравенствам на
ЭВМ.
от технологических параметров
процесса вытяжки с утонением стенки полых цилиндрических деталей из анизотропных
материалов устанавливались путем численных расчетов по этим неравенствам на
ЭВМ.
Графические
зависимости изменения предельного коэффициента утонения ![]() , вычисленного по первому
(11) и второму (12) критериям разрушения, от угла конусности матрицы
, вычисленного по первому
(11) и второму (12) критериям разрушения, от угла конусности матрицы ![]() для алюминиевого
сплава АМг6М приведены на рис. 3. Здесь кривая 1 соответствует величине
для алюминиевого
сплава АМг6М приведены на рис. 3. Здесь кривая 1 соответствует величине ![]() , определенной по
максимальной величине осевого напряжения
, определенной по
максимальной величине осевого напряжения
![]() на
выходе из очага пластической деформации (11); кривая 2 соответствует
величине
на
выходе из очага пластической деформации (11); кривая 2 соответствует
величине ![]() ,
вычисленной по степени использования ресурса пластичности (12) при
,
вычисленной по степени использования ресурса пластичности (12) при ![]() ; кривая 3 – при
; кривая 3 – при ![]() ; кривая 4 -
; кривая 4 - ![]() . Расчеты
выполнены при
. Расчеты
выполнены при ![]() ;
;
![]() ;
; ![]() мм;
мм; ![]() =40 мм. Положения
кривых 1 – 4 определяют возможности деформирования заготовки в зависимости от
технических требований на изделие.
=40 мм. Положения
кривых 1 – 4 определяют возможности деформирования заготовки в зависимости от
технических требований на изделие.

Рис. 3.
Графические зависимости изменения ![]() от
от ![]()
Анализ графиков и результатов расчета показывает, что с
увеличением угла конусности матрицы ![]() и коэффициента трения на контактной
поверхности матрицы
и коэффициента трения на контактной
поверхности матрицы ![]() , уменьшением относительной величины
, уменьшением относительной величины
![]() предельный
коэффициент утонения
предельный
коэффициент утонения ![]() увеличивается. Полученные результаты
качественно и количественно согласуются с экспериментальными данными, полученными
другими авторами [2].
увеличивается. Полученные результаты
качественно и количественно согласуются с экспериментальными данными, полученными
другими авторами [2].
Показано существенное влияние
анизотропии механических свойств на силовые режимы и предельные возможности
формообразования вытяжки с утонением стенки толстостенных цилиндрических
деталей. Установлено, что величины относительного напряжения и силы
увеличиваются с ростом коэффициента нормальной анизотропии ![]() . Увеличение коэффициента
анизотропии
. Увеличение коэффициента
анизотропии ![]() от
0,2 до 2 приводит к росту относительных величин осевого напряжения
от
0,2 до 2 приводит к росту относительных величин осевого напряжения ![]() на 50%, а силы
на 50%, а силы ![]() - на 30%.
Показано, что рост коэффициента анизотропии
- на 30%.
Показано, что рост коэффициента анизотропии ![]() от 0,2 до 2 сопровождается
увеличением предельного коэффициента утонения
от 0,2 до 2 сопровождается
увеличением предельного коэффициента утонения ![]() на 30%.
на 30%.
Литература
1. Яковлев С.С. Математическая модель процесса вытяжки с утонением стенки толстостенных цилиндрических заготовок из анизотропного материала / С.С. Яковлев, О.В. Пилипенко, А.И. Агеева // Известия ТулГУ. Серия. Механика деформируемого твердого тела и обработка металлов давлением. - Тула: Изд-во ТулГУ, 2006. – Вып. 2. – С. 69 – 77.
2. Яковлев С.П. Обработка давлением анизотропных материалов / С.П. Яковлев, С.С. Яковлев, В.А. Андрейченко. - Кишинев: Квант. - 1997.- 331 с.
3. Сторожев М.В. Теория обработки металлов давлением / М.В. Сторожев, Е.А. Попов. - М.: Машиностроение, 1977. - 423 с.
4. Колмогоров В.Л. Механика обработки металлов давлением / В.Л. Колмогоров. – Екатеринбург: Уральский государственный технический университет (УПИ), 2001. – 836 с.
5. Богатов А.А. Ресурс пластичности металлов при обработке давлением / А.А. Богатов, О.И. Мижирицкий, В.С. Смирнов. - М.: Металлургия, 1984. - 144 с.
6. Богатов А.А. Механические свойства и модели разрушения металлов / А.А. Богатов. – Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2002. – 329 с.
Публикации с ключевыми словами: вытяжка с утонением стенки
Публикации со словами: вытяжка с утонением стенки
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||
 ;
;
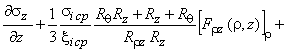
 ,
,


