научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 8, август 2008
УДК 621.73.07:658.58
Симушкин А.В.
МГТУ им. Н.Э. Баумана
Кафедра «Технология обработки материалов»
Научный руководитель: д.т.н., проф. Головин А.А.
ВВЕДЕНИЕ
Чаще всего кулачковые механизмы применяются в несиловых элементах машин. В случае применения их в силовых элементах, например, в газораспределительных механизмах двигателей внутреннего сгорания, где изменение размеров элементов кулачкового механизма может быть существенным, применяют различные компенсаторы образующихся зазоров. Можно назвать, по крайней мере, две причины, из-за которых конструктора избегают применять кулачковые механизмы в силовых элементах машин. Во-первых, вероятность повышенного износа элементов кулачкового механизма по сравнению с элементами, например, шарнирного соединения. Эта причина неустранима. Второй причиной можно считать неудачное проектирование механизма, связанное, в первую очередь с выбором закона движения толкателя. Однако вопросам износа кулачковых механизмов уделяется недостаточно внимания [1, 2, 3, 4]. Иногда предлагаются неудачные примеры и невероятные объяснения [5, стр.231-232]. В предлагаемой работе сделана такая попытка. В качестве объекта исследования взят гибочный пресс-автомат, в состав которого входят шесть кулачковых механизмов (рис.1; шестой механизм находится в зоне привода). Проведено исследование износа кулачковых механизмов и предлагается его имитационная модель. Результаты исследования демонстрируются на примере наиболее изношенного кулачкового механизма.

Рис.1. Гибочный пресс автомат
- ОПРЕДЕЛЕНИЕ РАЗМЕРОВ КУЛАЧКОВЫХ МЕХАНИЗМОВ МЕТОДОМ ЦИФРОВОЙ ФОТОСЪЁМКИ.
Определение размеров кулачкового механизма проводилось на основе съемки цифровой фотокамеры. Определены возможные ошибки измерений при непараллельности и несоосности торцевой плоскости кулачка и фокальной плоскости фотоаппарата. Последовательность перехода от фотографии к чертежу кулачкового механизма приведена на рис.2. Цифровое фото обработано при помощи программного пакета AutoDesk AutoCAD путем пятикратного обвода контура кулачка. Замеры перемещения толкателя и профильного угла кулачка проводились через каждые 5о поворота кулачка. В результате обработки замеров методами математической статистики [13] построен профиль кулачка и воспроизведен кулачковый механизм.

Рис.2. Последовательность определения размеров кулачка и кулачкового механизма.
Далее методом обращенного движения построена функция положения кулачкового механизма (рис.3a). Для учета нагрузки на сопрягаемые поверхности рис.3б нанесены:
1. нагрузка от пружины Fsp, осуществляющей силовое замыкание кинематической пары;
2. схематизированный график силы сопротивления Fdef, действующей на толкатель. Соотношение между этими нагрузками будет дано в п.4.
2. ПОСТРОЕНИЕ МЕТРИЧЕСКИХ ХАРАКТЕРИСТИК КУЛАЧКОВОГО МЕХАНИЗМА ПО ЭКСПЕРИМЕНТАЛЬНЫМ ДАННЫМ. ВОССТАНОВЛЕНИЕ ИСХОДНЫХ МЕТРИЧЕСКИХ ХАРАКТЕРИСТИК.
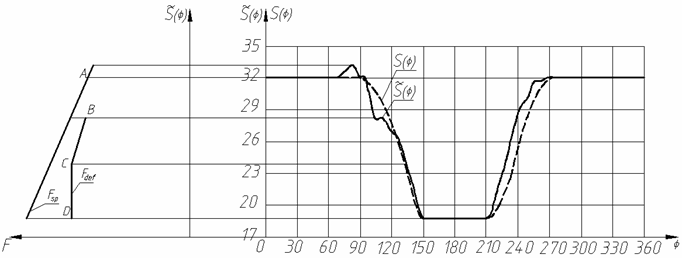
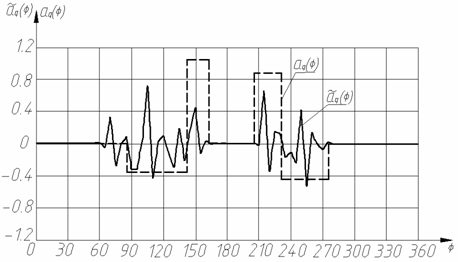
На рис.3 (кривые 1) приведены зависимости, построенные по экспериментальным данным:
- функция положения
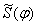 (рис.3а),
(рис.3а), - аналог скорости
 (рис.3в),
(рис.3в), - аналог ускорения
 (рис.3г).
(рис.3г).
Сравнение функции положения ![]() и исходной тактограммы, а
также сам вид графика механизма показывает, что кулачок существенно
изношен. Восстановление исходной формы функции положения основано на
анализе возможных схематизированных зависимостей аналогов скорости, которые
принимались при проектировании кулачковых механизмов того времени. В основу
восстановления исходных зависимостей положены следующие положения:
и исходной тактограммы, а
также сам вид графика механизма показывает, что кулачок существенно
изношен. Восстановление исходной формы функции положения основано на
анализе возможных схематизированных зависимостей аналогов скорости, которые
принимались при проектировании кулачковых механизмов того времени. В основу
восстановления исходных зависимостей положены следующие положения:
· заданный ход толкателя h;
· определение начальной точки подъема толкателя в соответствии с циклограммой;
· выбор наиболее вероятного закона изменения аналога скорости Vq [3], исходя из заданного хода толкателя.
 (1)
(1)
На рис.3 экспериментально полученные кривые помечены сплошными линиями, восстановленные зависимости – пунктирными.
- ПОСТРОЕНИЕ КАРТИНЫ ИЗНОСА КОНТУРА КУЛАЧКА ПО РЕЗУЛЬТАТАМ ЭКСПЕРИМЕНТА.
По восстановленной функции положения построен исходный профиль кулачка, на который наложен профиль изношенного кулачка (рис.4). На контур нанесены точки, характеризующие начало соответствующих фаз работы механизма:
-
- A – начало подъема толкателя;
- B – точка начала контакта ползуна с заготовкой;
- C – сила деформирования становиться постоянной;
- D – прекращение действия силы деформирования;
- F – начало обратного хода ползуна;
- E – остановка толкателя.
Наибольший износ профиля наблюдается в зоне совместной нагрузки от силы деформирования и пружины C-D. Максимальный износ наблюдается в окрестности точки D, соответствующей наименьшему радиусу кривизны профиля и скачку ускорения. Сравнение нагруженной (A-D) и ненагруженной (F-E) ветвей профиля позволяет определить соотношение между нагрузкой пружины и силой сопротивления:
![]() (2)
(2)
где
Fdef - сила деформирования;
Fsp – сила от действия пружины;
Δ fs – износ кулачка при рабочем ходе;
Δ rs – износ кулачка при обратном ходе.
б) а)

в)
г)
Рис.3. Экспериментальные и восстановленные зависимости функции положения и аналогов скорости и ускорения.

Рис.4. Сравнение исходного и изношенного контура кулачка.
- ПОСТРОЕНИЕ ИМИТАЦИОННОЙ МОДЕЛИ ИЗНОСА КОНТУРА КУЛАЧКА.
Имитационная модель начальной фазы износа построена в соответствии с формулой Герца. Все размеры отнесены к величине полного хода толкателя h.
![]() (3)
(3)
где
![]() -
вертикальная составляющая реакции в точке контакта;
-
вертикальная составляющая реакции в точке контакта;
![]() -
угол давления в высшей паре;
-
угол давления в высшей паре;
![]() - радиус
кривизны роликового толкателя и профиля кулачка в точке контакта.
- радиус
кривизны роликового толкателя и профиля кулачка в точке контакта.
В ее основе лежит разделение источников износа на две составляющие. Первая составляющая показывает влияние геометрии кулачка (рис.5а) и определяется по формуле
![]() (4)
(4)
![]() – геометрический аналог
нагрузки, учитывающий радиус кривизны профиля кулачка в точке контакта и радиус
ролика.
– геометрический аналог
нагрузки, учитывающий радиус кривизны профиля кулачка в точке контакта и радиус
ролика.
Вторая составляющая показывает влияние нагрузки (рис.5б) и определяется по формуле
![]() (5)
(5)
![]() -
аналог нагрузки, учитывающий реакцию от силы, действующей на кулак в
точке контакта.
-
аналог нагрузки, учитывающий реакцию от силы, действующей на кулак в
точке контакта.
Эпюра износа
соответствует формуле (![]() (6))
и показана на рис.5в.
(6))
и показана на рис.5в.
|
|
|
|
|
a) |
б) |
в) |
Рис.5. Имитационная модель износа кулачка.
- СРАВНЕНИЕ РЕАЛЬНОГО ИЗНОСА И ИЗНОСА ПО ИМИТАЦИОННОЙ МОДЕЛИ.
На рис.6 приведено качественное сравнение реального износа кулачка (кривая w) и начальной фазы износа по имитационной модели (кривая σ). Кривые износа построены на контуре кулачка. Для сравнительного анализа результатов приведены зависимости нагрузки и восстановленного аналога ускорения.

Рис.6. Качественное сравнение реального износа и его имитационной модели.
Сравнительный анализ реального и теоретического износов проведен в таблице.
|
Характерные точки контура |
реальный износ |
износ по имитационной модели |
|
A |
смещение начальной точки |
смещение начальной точки |
|
AB |
нарастание износа |
нарастание износа |
|
B |
max 1 |
снижение gradw |
|
BC |
уменьшение износа |
нарастание износа |
|
C |
min |
перегиб |
|
CD |
max 2 |
высокий градиент нарастания износа |
|
D |
min |
max |
|
DE |
const |
const |
|
E |
const |
const |
|
EF |
max 3 |
уменьшение износа |
|
F |
const |
const |
Таким образом, можно отметить качественное совпадение реального и теоретического износа.
ВЫВОДЫ
- По результатам цифровой фотосъёмки получена зависимость функции положения кулачкового механизма, обработанная методом статистической обработки эксперимента. По обработке экспериментальных данных получены зависимости аналогов скорости и ускорения.
- По экспериментально полученному аналогу скорости восстановлена исходная зависимость аналога скорости и получены исходные зависимости функции положения и аналога ускорения и восстановлен исходный профиль кулачка.
- На основании формулы Герца для контактных напряжений построена имитационная модель износа профиля кулачка.
- Сравнение восстановленного и изношенного профиля кулачка позволило получить картину износа кулачка. Сравнение реальной картины износа и износа по имитационной модели показало приемлемость предложенной имитационной модели.
ЛИТЕРАТУРА
- Теория механизмов и механика машин: Учеб. для втузов/К.В. Фролов, С.А. Попов, А.К. Мусатов и др.; Под ред. К.В. Фролова. – 2-е изд., перераб. и доп. – М.: Высш. шк., 1998. – 496 с.
- Решетов Д.Н. Детали машин: Учеб. для ст-тов машиностроит. и механических спец-тей вузов. – 4-е изд., перераб. и доп. – М.: Машиностроение, 1989. – 496 с.
- Юдин В.А., Петрокас Л.В. Теория механизмов и машин. Учеб. Пособие для втузов. Изд. 2-е перераб. и доп. – М.: Высшая школа, 1977. – 527 с.
- Решетов Л.Н. Кулачные механизмы токарных станков. – М.-Л.: ОНТИ, 1935. – 43 с., ил.
- Кожевников С.Н. Теория механизмов и машин. Учебное пособие для студентов втузов. Изд. 4-е исправленное. – М.: Машиностроение. – 592 с.
- Шульц В.В. Точность и износ // Сб. «Фундаментальные проблемы теории точности» / Под ред. В.П. Булатова и И.Г. Фридлендера. – СПб.: Наука, 2001. – 504 с.
- Jan De Fraine Reverse engineering of cams //Proceedings the 10-th Congress on the Theory of Machines and Mechanisms, Oulu, Finland, Vol.1, 1999. Pp. 404-410
- A.Golovin A. Borisov, A. Ermakova Some Examples from History of Machinery in TMM Teaching // Proceeding of International Symposium on History of Machines and Mechanisms, Kluwer Academic Publishers, 2004. PP.107-118.
- M.Ceccarelli, G.Carbone, E.Ottaviano and C.Lanni An opTimum Design of Cam Profiles with Circular Arcs// Edited CT 2005 CD-Volume on an Transmissions: functional and dynamical aspects Cassino and Napoli: 25 November 2005.
- M.Ceccarelli, C.Lanni, G.Carbone A Fairly Simple Method to Identify the Curvature of a Cam Profile// Edited CT 2005 CD-Volume on an Transmissions: functional and dynamical aspects Cassino and Napoli: 25 November 2005.
11. V.Niola G.Quaremba A multivariate Methodology for Dynamical Analysis of a Cam-Follower System // Edited CT 2005 CD-Volume on an Transmissions: functional and dynamical aspects Cassino and Napoli: 25 November 2005.
12. A.Golovin, A.Borisov, A.Oskin Geometrical Analogues of Contact Stress for Cams Design // Edited CT 2005 CD-Volume on an Transmissions: functional and dynamical aspects Cassino and Napoli: 25 November 2005.
13. A.Golovin Researching of mechanical efficiency with methods of active planning of experiment, Moscow, 1984. – 9 p.
Публикации с ключевыми словами: кулачковый механизм
Публикации со словами: кулачковый механизм
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||






